Im letzten Abschnitt ist es uns gelungen, den Impuls als physikalische Größe über Stoßvorgänge zu definieren und eine Messvorschrift für den Zusammenhang zwischen Impuls und Geschwindigkeit zu finden.
Unser Ziel in diesem Kapitel ist es nun, einen völlig neuen Aspekt in diese Betrachtung mit hinzuzunehmen und daraus mit etwas Glück den Zusammenhang zwischen Impuls und Geschwindigkeit ermitteln zu können.
Wir wollen uns mit der Symmetrie von Zusammenstößen befassen. Dabei wird der Begriff Symmetrie in der Physik in einem umfassenderen Sinn verwendet als in der Umgangssprache. Gemeint ist folgendes:
Um einen physikalischen Vorgang zu beschreiben, müssen die physikalischen Größen in einem bestimmten Referenzsystem angegeben werden. Man benötigt Koordinaten für Raum und Zeit, man gibt in der Quantenmechanik Wellenfunktionen an oder in der Elektrodynamik elektromagnetische Potentiale. Es stellt sich aber heraus, dass man bei der Wahl des Referenzsystems bestimmte Freiheiten hat. So kann man das Raum-Koordinatensystem drehen oder verschieben, man kann die Phase von Wellenfunktionen global drehen oder die elektromagnetischen Potentiale umeichen, ohne dass dadurch die Beschreibung des physikalischen Prozesses beeinträchtigt wird. Man hat die Freiheit, unter mehreren gleichwertigen Referenzsystemen zu wählen. Diese Freiheit bezeichnet man als Symmetrie des physikalischen Problems.
Die Betrachtung von solchen Symmetrien hat sich in der modernen Physik als sehr fruchtbar erwiesen. Symmetrien bilden den wesentlichen Grundpfeiler aller modernen physikalischen Theorien, die sich mit den grundlegenden Naturgesetzen befassen.
Versuchen wir also, Symmetrien bei unseren Zusammenstößen aufzuspüren. Wir hatten Zusammenstöße aus dem Grund betrachtet, weil sich vorher und nachher die Teilchen in einer geradlinig gleichförmigen Bewegung befinden. Diese Bewegungsform hatten wir als besonders einfach angesehen, weil wir zu ihrer Erklärung keine weiteren physikalischen Begriffe mehr benötigen (dies haben wir zumindest angenommen). Die geradlinig gleichförmige Bewegung eines Objektes haben wir gleichsam als Grundform der Bewegung angesehen.
Es liegt daher nahe, Symmetrien zu betrachten, die eine Grundform der Bewegung in eine andere Grundform der Bewegung überführen. Wir wollen also mathematische Transformationen betrachten, die eine geradlinig gleichförmige Bewegung in eine andere geradlinig gleichförmige Bewegung überführen. Anders ausgedrückt: wir wollen Wechsel des Raum-Zeit-Koordinatensystems betrachten, so dass die Bewegung aus dem neuen System heraus betrachtet wieder eine geradlinig gleichförmige Bewegung ist.
Einige Beispiele: Wir könnten den Nullpunkt des Koordinatensystems verschieben. Wir könnten die Bewegung von einem Zug aus betrachten, der sich mit konstanter Geschwindigkeit bewegt. Wir könnten das Koordinatensystem um 90 Grad nach links drehen.
Ein Gegenbeispiel: Wenn wir eine geradlinig gleichförmige Bewegung aus einem beschleunigenden Auto heraus betrachten, so erscheint diese Bewegung nicht mehr geradlinig gleichförmig. Ein solcher Wechsel des Koordinatensystems ist also keine Symmetrie mehr für unsere Grundform der Bewegung.
Damit wir keine Symmetrie übersehen, wollen wir uns von der Anschauung wieder lösen und möglichst streng mathematisch vorgehen. Welches sind die Transformationen, die eine geradlinig gleichförmige Bewegung wieder in eine geradlinig gleichförmige Bewegung umwandeln?
Normalerweise beschreiben wir eine solche Bewegung durch eine Bahnkurve im 3-dimensionalen Raum. Kurvenparameter ist dabei die Zeit. Wir schreiben also \[ \boldsymbol{x} = \boldsymbol{x}_0 + \boldsymbol{v} t \] Dabei ist \(\boldsymbol{x}\) der Ort des Objektes zur Zeit \(t\), \(\boldsymbol{x}_0\) ist der Ort zur Zeit Null und \(\boldsymbol{v}\) ist die konstante Geschwindigkeit des Objektes. Zur Zeit \(t\) befindet sich das Objekt also am Ort \(\boldsymbol{x}_0\) plus der konstanten Geschwindigkeit \(\boldsymbol{v}\) mal der Zeit \(t\).
Diese Darstellung ist für unsere Zwecke allerdings wenig geeignet. Den Grund dafür werden wir allerdings erst etwas weiter unten einsehen. Momentan soll die Bemerkung genügen, dass wir die Zeit lieber analog zu einer Raumkoordinate behandeln sollten und nicht als Parameter, der einerseits in der Bahnkurve und andererseits eventuell in der gesuchten Transformation enthalten ist. Das führt schnell zu Verwirrungen und zu Fehlern.
Statt den dreidimensionalen Raum wollen wir einen vierdimensionalen Raum betrachten, der die drei gewöhnlichen Raumkomponenten sowie eine Zeitkomponente umfasst und den man auch als Raumzeit bezeichnet. Ort \(\boldsymbol{x}\) und Zeit \(t\) fassen wir zu einem vierdimensionalen Raum-Zeit-Vektor \(x\) zusammen: \[ x := \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} \] Wir wollen im folgenden die Zeitkomponente mit dem Koordinatenindex Null versehen, damit die drei Raumkomonenten ihre gewohnten Indices 1, 2 und 3 behalten können.
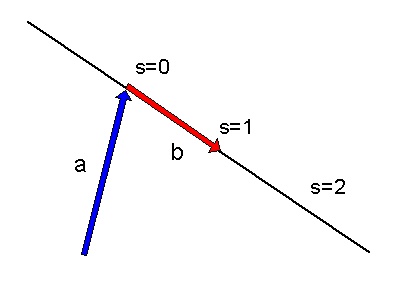
Eine geradlinig gleichförmige Bewegung wird auch im vierdimensionalen
Raum durch eine Gerade dargestellt, die wir so schreiben wollen:
\[
x = a + b s
\]
Dabei sind \(x, a\) und \(b\) vierdimensionale Vektoren und \(s\) ist der
reelle Kurvenparameter.

Wenn wir als Kurvenparameter \(s\) die Zeit \(t\) wählen, so finden wir als Zusammenhang mit der dreidimensionalen Darstellung die Formeln \[ a = \begin{pmatrix} 0 \\ \boldsymbol{x}_0 \end{pmatrix} \] \[ b = \begin{pmatrix} 1 \\ \boldsymbol{v} \end{pmatrix} \] sodass die Geradengleichung \(x = a + b s\) so aussieht: \[ \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} 0 \\ \boldsymbol{x}_0 \end{pmatrix} + \begin{pmatrix} 1 \\ \boldsymbol{v} \end{pmatrix} \cdot s \] also \begin{align} t &= s \\ \boldsymbol{x} &= \boldsymbol{x}_0 + \boldsymbol{v} t \end{align}
Wir wollen uns jedoch auf keine spezifische Parametrisierung der Bahnkurve festlegen. Wichtig ist für uns nur, dass sie eine Gerade in vierdimensionalen Raum ist. Übrigens ist im Gegensatz zur dreidimensionalen Darstellung hier jede geradlinig gleichförmige Bewegung eine Gerade, da auch ein ruhendes Objekt sich in der Zeit fortbewegt. Wir müssen also in der obigen Darstellung immer fordern, dass die Zeitkomponente (d.h. die oberste oder auch nullte Komponente) von \(b\) ungleich Null ist.
Die Frage, die wir uns stellen, lautet nun: Welche mathematischen Abbildungen können wir auf den 4-dimensionalen Raum \(\mathbb{R}^4\) wirken lassen, damit aus jeder Geraden in diesem Raum wieder eine Gerade wird? Gesucht sind also Abbildungen \[ g : \, \mathbb{R}^4\ \rightarrow \mathbb{R}^4\ \] so dass \[ g(a + b s) = a' + b' s \] Dabei sind alle 4-dimensionalen Vektoren \(a, b, a', b'\) von \(s\) unabhängig, damit durch die Formeln Geraden im vierdimensionalen Raum parametrisiert werden, die gleichmäßig mit wachsendem Parameter \(s\) durchlaufen werden, sodass die Bewegung geradlinig-gleichförmig ist. Die Forderung gilt für beliebige Vektoren \(a\) und \(b\).
Hier wird noch einmal der Unterschied unserer vierdimensionalen Herangehensweise im Vergleich zu einer dreidimensionalen Vorgehensweise deutlich. Dadurch, dass wir die Zeit analog zu einer Raumdimension behandeln, erfassen wir auch Transformationen der Zeit in einfacher Weise gleich mit. Wir betrachten Transformationen von Raum und Zeit, nicht nur Transformationen des Raums. Zugegeben: auf die Idee musste ein schlauer Kopf erst einmal kommen, und auf der Hand liegt das keineswegs!
Was können wir nun aus dieser Forderung für die Abbildung \(g\) ableiten?
Wenn wir den speziellen Parameterwert \(s = 0\) wählen, so folgt unmittelbar \[ a' = g(a) \] Weiterhin ist nach Voraussetzung \(b'\) unabhangig von \(s\), d.h. wir können \(b'\) als eine Funktion \(h\) von \(a\) und \(b\) schreiben, also \[ b' = h(a,b) \]
Die Bedingung für \(g\) lässt sich also umschreiben als \[ g(a + b s) = g(a) + h(a,b) \, s \] Was können wir noch herausfinden? Um das zu überprüfen, bilden wir die Ableitung dieser Gleichung nach \(s\). Dabei machen wir noch eine subtile Voraussetzung:
Wir fordern, dass die Abbildung \(g\) nicht selbst vom Parameter \(s\) abhängt!
Wären wir im dreidimensionalen Raum geblieben, hätten wir dort die Zeit \(t\) als Kurvenparameter gewählt, und hätten wir an dieser Stelle analog gefordert, dass die Abbildung nicht vom Kurvenparameter \(t\) abhängt, so wären uns beispielsweise alle die Abbildungen entgangen, bei denen sich ein Bezugssystem relativ zu einem anderen bewegt. Man sieht, wie subtil diese Überlegungen sind, wie schnell man etwas übersieht und wie sehr es darauf ankommt, den geeigneten mathematischen Rahmen zu finden.
Die Ableitung der obigen Gleichung nach \(s\) ergibt \[ Dg(a+bs) \cdot b = h(a,b) \] Dabei meint \(Dg\) die Matrix der Ableitungen der einzelnen Komponenten der Funktion \(g\) nach den einzelnen Variablen, von denen \(g\) abhängt. In Klammern ist die Stelle angegeben, an der die Ableitung ausgewertet wird. Um nicht in Indices zu ertrinken, haben wir die Matrixschreibweise verwendet, d.h. der Punkt \(cdot\) meint die Matrixmultiplikation. Setzen wir nun \(s = 0\) ein und vertauschen rechte und linke Seite, so folgt \[ h(a,b) = Dg(a) \cdot b \] \(h\) hängt also linear von \(b\) ab. Bleibt die Frage, ob die Matrix \(Dg\) überhaupt von \(a\) abhängt.
Dazu setzen wir unser Zwischenergebnis \( h(a,b) = Dg(a) \cdot b \) in unsere Ausgangsgleichung \( g(a + b s) = g(a) + h(a,b) \, s \) ein: \[ g(a + b s) = g(a) + Dg(a) \cdot b \cdot s \] Wir setzen hier \(s = 1\) ein und leiten nach den Komponenten von \(b\) ab: \[ Dg(a + b) = Dg(a) \] d.h. die Matrix \(Dg\) kann nicht von ihrem Argument abhängen. Sie ist eine konstante Matrix, die wir mit \(A\) bezeichnen wollen. Also haben wir \[ h(a,b) = A \, b \] Eingesetzt in unsere Ausgangsgleichung \( g(a + b s) = g(a) + h(a,b) \, s \) ergibt sich \[ g(a + b s) = g(a) + A \, b \, s \] Erinnern wir uns: dies ist eine Bedingung an die Abbildung \(g\). Sie enthält immer noch denselben Informationsgehalt wie in ihrer ursprünglichen Form \(g(a + b s) = a' + b' s\). Die Bedingung gilt natürlich auch für den Spezialfall \(a = 0\) und \(s = 1\). Dieser Spezialfall genügt nun, um die Abbildung \(g\) eindeutig festzulegen. Setzen wir also \(a = 0\) und \(s = 1\) oben ein: \[ g(b) = g(0) + A \, b \] Den konstanten Vektor \(g(0)\) nennen wir \(c\) und tauschen ihn nach rechts, und wir schreiben \(x\) statt \(b\): \[ g(x) = A \, x + c \] Das ist also nun das Ergebnis!
So muss die Abbildung aussehen, damit Geraden wieder auf Geraden abgebildet werden, die gleichmäßig mit dem Parameter \(s\) durchlaufen werden, wobei die Abbildung selbst nicht vom Parameter \(s\) abhängt.
Man bezeichnet diese speziellen Abbildungen
auch als affine Abbildungen. Die affine Abbildung beinhaltet
eine lineare Abbildung (gegeben durch die Matrix \(A\)) sowie eine
Verschiebung (gegeben durch den Verschiebungsvektor \(c\)).
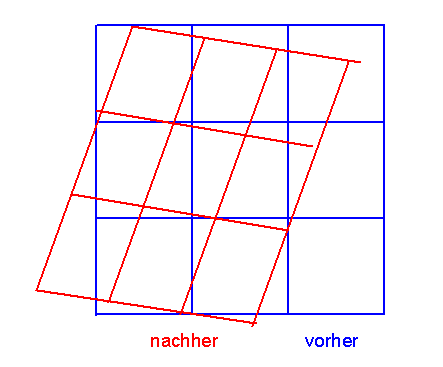
Lassen wir diese Abbildung auf die Gerade \(x = a+bs\) wirken: \[ g(a+bs) = \] \[ = A \, (a+bs) + c = \] \[ = A a + c + A b s \] d.h. für die neue Gerade \(g(x) = a' + b' s\) gilt der Zusammenhang \(a' = A a + c\) sowie \(b' = A b\). Als Nebenbemerkung sei noch erwähnt, dass die Zeit-Zeit-Komponente (oder auch Null-Null-Komponente) der Matrix \(A\) nicht Null sein darf, da die Zeitkomponente (nullte Komponente) von \(b'\) und \(b\) nie Null sein dürfen, damit sich das Objekt in der Zeit fortbewegen kann.
Die Abbildung \(g\) hängt von 20 Parametern ab, nämlich von den vier Komponenten des Verschiebevektors \(c\) und den 16 Komponenten der Matrix \(A\). Wenn wir diese Parameterabhängigkeit besonders betonen wollen, können wir sie als Index an die Abbildung \(g\) anfügen, d.h. wir schreiben dann \[ g_{A, c}(x) \] Die Menge aller affinen Abbildungen besitzt eine Gruppenstrukur. Die Abbildungen sind dabei die Gruppenelemente, und die Verknüpfung zweier Gruppenelemente ist gegeben durch das Nacheinander-Ausführen zweier affiner Abbildungen.
Führen wir also erst die affine Abbildungen \(g_{A,c}\) und danach die affine Abbildung \(g_{B,d}\) aus: \[ g_{B,d} \, (g_{A,c} (x) \, ) = \] \[ = B (A \, x + c) + d = \] \[ = B A \, x + B c + d = \] \[ g_{B A, B c + d}(x) \] Die Gruppenstruktur der affinen Abbbildunegn lautet also \[ g_{B,d} \circ g_{A,c} = g_{B A, B c + d} \] wobei \( \circ \) die Verkettung (Gruppenmultiplikation) der beiden affinen Abbildungen bedeutet, also deren Hintereinander-Ausführen.
Dass diese Verkettung eine Gruppenstruktur bildet, muss man natürlich noch überprüfen:
Wir sehen also, dass alle Gruppenaxiome erfüllt sind. Allerdings bilden affine Abbildungen im Allgemeinen keine abelsche Gruppe, d.h. die Gruppenelemente können nicht miteinander vertauscht werden. Es ist nicht egal, in welcher Reihenfolge die affinen Abbildungen ausgeführt werden.
Eine letzte Bemerkung: Wir hatten gefordert, dass Geraden wieder auf Geraden abgebildet werden sollen. Wir hatten Transformationen in Raum und Zeit gesucht, die das gewährleisten und für diese Transformationen die Forderung \(g(a+bs) = a'+b's\) aufgestellt. Diese Forderung beinhaltet aber mehr, als dass nur Geraden auf Geraden abgebildet werden sollen. Sie sagt auch, dass die bestimmte von uns gewählte Parametrisierung wieder in eine Parametrisierung gleicher Form überführt werden soll. Anschaulich bedeutet das, dass jede Gerade vor und nach der Raum-Zeit-Transformation bei wachsendem Parameter \(s\) gleichmäßig durchlaufen wird. Dies entspricht dem Bild der geradling-gleichförmigen Bewegung und wird von uns als Forderung an die Transformation daher gern akzeptiert. Genau genommen hatten wir ja nicht nur gefordert, dass Geraden wieder auf Geraden abgebildet werden, sondern dass eine geradlinig gleichförmige Bewegung wieder in eine geradlinig gleichförmige Bewegung transformiert wird. Der Parameter \(s\) muss also auf einfache Weise mit der Zeit \(t\) zusammenhängen: gleichmäßiges Fortschreiten von \(t\) muss gleichmäßiges Fortschreiten von \(s\) bedeuten (wenn auch nicht unbedingt mit derselben Geschwindigkeit).
© Jörg Resag, www.joerg-resag.de
last modified on 18 June 2023