Wir haben im letzten Abschnitt die verallgemeinerte und die eigentliche Galileigruppe kennengelernt. Die Matrizen dieser Gruppen haben wir aus der Forderung abgeleitet, dass die Matrix A keine zeitlichen Abstände ändern darf. Damit sind die Matrizen A von der Form \[ A = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{u} & R \end{pmatrix} \] und wirken auf Raum und Zeit in der folgenden Weise: \[ A x = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{u} & R \end{pmatrix} \, \begin{pmatrix} t \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} t \\ \boldsymbol{u} t + R \boldsymbol{x} \end{pmatrix} \] (wobei wir Zeitspiegelungen erst mal unterschlagen wollen). Bei den Matrizen der eigentlichen Galileigruppe fordert man zusätzlich, dass die räumlichen Abstände in einer Zeitscheibe der Raumzeit nicht geändert werden dürfen. Die Matrix \(R\) muss dann eine orthogonale Matrix sein, also \[ R^T \, R = \mathbb{1} \] erfüllen.
Sind diese mathematischen Transformationen in Raum und Zeit nun sinnvolle Symmetrietransformationen der Naturgesetze? Muss man sich auf die eigentliche Galileigruppe beschränken, oder ist sogar die verallgemeinerte Galileigruppe eine Symmetrietransformation?
Um diese Fragen zu beantworten, wollen wir untersuchen, was die Galileitransformationen für unsere Stoßexperimente und für den Zusammenhang zwischen Geschwindigkeit und Impuls bedeuten würde.
Betrachten wir einen Zusammenstoß von zwei Objekten. Angenommen, die obige Abbildung \(A\) wäre tatsächlich eine Symmetrietransformation der Natur. Dann könnten wir die Geschwindigkeit \(\boldsymbol{v}\) jedes Objektes (vor und nach dem Zusammenstoß) in eine neue Geschwindigkeit \(\boldsymbol{u} + R \boldsymbol{v}\) transformieren, und der Zusammenstoß mit diesen neuen Geschwindigkeiten wäre wieder ein Vorgang, wie er so in der Natur ablaufen könnte. Aus einem einzigen Stoßvorgang könnten wir so sehr viele andere mögliche Stoßvorgänge konstruieren. Ob dies in der Natur auch tatsächlich so ist, muss mit Hilfe von Experimenten geprüft werden.
Nicht nur die Geschwindigkeiten müssen wir verändern, sondern auch die Impulse müssen in neue Impulse umgewandelt werden. Dabei müssen die neuen Impulse mit den neuen Geschwindigkeiten zusammenpassen und die Summe der neuen Impulse vor und nach dem Zusammenstoß muss wieder gleich sein (Impulserhaltung).
Prüfen wir also nach, ob die obigen Transformationen und die Impulserhaltung miteinander verträglich sind, und ob vielleicht sogar der Zusammenhang zwischen Impuls und Geschwindigkeit dadurch festgelegt wird.
Für den Zusammenhang zwischen dem Impuls \(\boldsymbol{p}\) und der Gechwindigkeit \(\boldsymbol{v}\) eines Teilchens machen wir den Ansatz \[ \boldsymbol{p} = f(|\boldsymbol{v}|) \, \boldsymbol{v} \] d.h. der Impuls zeigt in Richtung der Geschwindigkeit, der Betrag des Impulses hängt eindeutig über die Funktion f vom Betrag der Geschwindigkeit ab, und für die Geschwindigkeit Null ist auch der Impuls gleich Null.
Dieser Ansatz erfüllt alle unsere Bedingungen an den Zusammenhang zwischen Impuls und Geschwindigkeit, die wir in einem vorhergehenden Abschnitt gestellt haben.
Voraussetzung war, dass sich das Teilchen auch in Ruhe befinden kann, d.h. dass die Geschwindigkeit Null für das Teilchen überhaupt möglich ist. Wenn die Galileitransformationen andererseits Symmetrietransformationen für die Physik sein sollen, so muss für jedes Teilchen die Geschwindigkeit Null möglich sein. Zu jeder beliebigen geradlinig gleichförmigen Bewegung eines Teilchens kann man nämlich leicht eine Galileitransformation angeben, so dass nach dieser Transformation das Teilchen die Geschwindigkeit Null aufweist. Man muss lediglich \(\boldsymbol{u}\) und \(R\) so wählen, dass \( \boldsymbol{u} + R \boldsymbol{v} = 0 \) wird, also z.B. \(R = \mathbb{1}\) und \( \boldsymbol{u} = -\boldsymbol{v}\). Erinnern wir uns: Symmetrietransformation bedeutet, dass eine physikalisch mögliche Situation durch die Transformation in eine neue, ebenfalls mögliche physikalische Situation umgewandelt wird.
Wir betrachten nun den Fall, dass zwei identische Objekte zunächst zu einem größeren Objekt miteinander verbunden sind, das sich in Ruhe befindet. Diese Verbindung wird nun aufgehoben, und die beiden Objekte werden durch irgend etwas (z.B. eine Feder) auseinandergetrieben. Man kann sich auch vorstellen, dass ein ruhendes Objekt in zwei neue, einander gleiche Objekte auseinanderbricht, die dann entgegengesetzt zueinander auseinanderfliegen.
Wir hatten früher identische Teilchen so definiert, dass sie
bei diesem Experiment
mit gleicher Geschwindigkeit in entgegengesetzte Richtungen
auseinanderfliegen.
Die Geschwindigkeit von Teilchen (bzw. Objekt) 1 ist also \(\boldsymbol{v}\), die von
Teilchen 2 ist \(-\boldsymbol{v}\).

Aufgrund der Impulserhaltung müssen die Impulse der beiden auseinanderfliegenden Teilchen gleich dem Impuls des ruhenden Objektes sein, aus dem sie entstanden sind, also \[ \boldsymbol{p}_1 + \boldsymbol{p}_2 = 0 \] Dies geht streng genommen über die Impulserhaltung hinaus, wie wir sie bei den Zusammenstößen von Bällen früher bereits betrachtet haben. Wir wollen also die Impulserhaltung auch für diesen Fall noch einmal explizit einfordern.
Setzen wir nun \begin{align} \boldsymbol{p}_1 &= f_1(|\boldsymbol{v}|) \, \boldsymbol{v} \\ \boldsymbol{p}_2 &= f_2(|\boldsymbol{v}|) \, (-\boldsymbol{v}) \end{align} (denn \( |-\boldsymbol{v}| = |\boldsymbol{v}| \) ) oben ein, so folgt \[ f_1(|\boldsymbol{v}|) \, \boldsymbol{v} - f_2(|\boldsymbol{v}|) \, \boldsymbol{v} = 0 \] oder anders geschrieben \[ (f_1(|\boldsymbol{v}|) - f_2(|\boldsymbol{v}|)) \, \boldsymbol{v} = 0 \] Da diese Bedingung bei identischen Teilchen für beliebige Geschwindigkeiten \(\boldsymbol{v}\) richtig sein soll, muss die Klammer immer gleich Null sein, d.h. \[ f_1(|\boldsymbol{v}|) = f_2(|\boldsymbol{v}|) \] Also müssen die Funktionen \(f_1\) und \(f_2\) bei identischen Teilchen gleich sein – sie können nicht vom Teilchen abhängen. Identische Teilchen bedeutet also in diesem Sinne, dass die Teilchen die gleiche Funktion für den Zusammenhang zwischen Geschwindigkeit und Impuls besitzen. Nennen wir diese Funktion also einfach \(f\).
Bei nicht identischen Teilchen wird die Funktion dagegen vom Teilchen abhängen. Für das ruhende Objekt, das in die beiden identischen Teilchen auseinanderbricht, bezeichnen wir die Funktion also mit \(f_0\).
Wir lassen nun eine Galileitransformation auf den Raum und die Zeit wirken. Aus der Geschwindigkeit \(\boldsymbol{v}\) wird so die neue Geschwindigkeit \( \boldsymbol{u} + R \boldsymbol{v} \), aus \(-\boldsymbol{v}\) wird \( \boldsymbol{u} - R \boldsymbol{v} \), und aus der Geschwindigkeit Null des ruhenden Objektes wird die Geschwindigkeit \(\boldsymbol{u}\).
Die neue Situation sieht also so aus, als ob ein Objekt, das sich mit der
Geschwindigkeit \(\boldsymbol{u}\) bewegt, in zwei einander identische Objekte zerfällt,
die sich mit den Geschwindigkeiten \( \boldsymbol{u} + R \boldsymbol{v} \)
und \( \boldsymbol{u} - R \boldsymbol{v} \) bewegen.
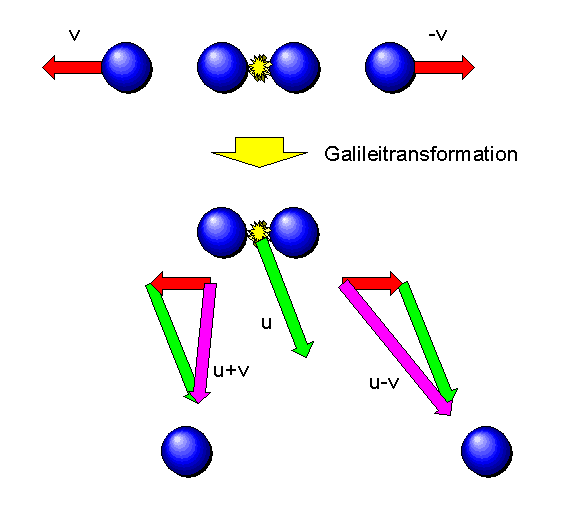
Wenn die Galileitransformation eine Symmetrietransformation sein soll, so muss diese neue Situation physikalisch möglich sein, und wir fordern daher, dass die Impulse der beiden identischen Teilchen zusammen gerade den Impuls des zerfallenden Objektes ergeben. Es muss also gelten: \[ \boldsymbol{p}'_1 + \boldsymbol{p}'_2 = \boldsymbol{P} \] mit dem Impuls \(\boldsymbol{P}\) des zerfallenden Objekts und den neuen Impulsen \(\boldsymbol{p}'_1\) und \(\boldsymbol{p}'_2\) nach der Transformation. Ausgedrückt durch die Geschwindigkeiten bedeutet das: \[ \; (\boldsymbol{u} + R \boldsymbol{v}) \, f(|\boldsymbol{u} + R \boldsymbol{v}|) + \] \[ + (\boldsymbol{u} - R \boldsymbol{v}) \, f(|\boldsymbol{u} - R \boldsymbol{v}|) = \] \[ = \boldsymbol{u} \, f_0(|\boldsymbol{u}|) \] oder links anders sortiert \[ \quad \; \boldsymbol{u} \cdot [ \, f(|\boldsymbol{u} + R \boldsymbol{v}|) + f(|\boldsymbol{u} - R \boldsymbol{v}|) \, ] + \] \[ + R \boldsymbol{v} \cdot [ \, f(|\boldsymbol{u} + R \boldsymbol{v}|) - f(|\boldsymbol{u} - R \boldsymbol{v}|) \, ] = \] \[ = \boldsymbol{u} \, f_0(|\boldsymbol{u}|) \] Diese Beziehung soll für alle Galileitransformationen gelten, also für alle Vektoren \(\boldsymbol{u}\) und \(R\boldsymbol{v}\), egal wie sie ausgerichtet sind.
Dies ist nur möglich, wenn folgendes gilt: \[ \quad \quad \; f(|\boldsymbol{u} + R \boldsymbol{v}|) + f(|\boldsymbol{u} - R \boldsymbol{v}|) = f_0(|\boldsymbol{u}|) \] \[ f(|\boldsymbol{u} + R \boldsymbol{v}|) - f(|\boldsymbol{u} - R \boldsymbol{v}|) = 0 \] Wenn wir nun die untere zur oberen Gleichung addieren bzw. die untere von der oberen Gleichung abziehen, so folgt \[ 2 \, f(|\boldsymbol{u} + R \boldsymbol{v}|) = f_0(|\boldsymbol{u}|) \] \[ 2 \, f(|\boldsymbol{u} - R \boldsymbol{v}|) = f_0(|\boldsymbol{u}|) \] Da die rechte Seite nicht von \(\boldsymbol{v}\) abhängt, kann auch die linke Seite nicht von \(\boldsymbol{v}\) abhängen. Es folgt, dass die Funktion \(f\) (und damit auch \(f_0\)) konstant ist. Wir wollen diese Konstante als Masse des Teilchens bezeichnen und mit dem Buchstaben \(m\) abkürzen: \[ f(|\boldsymbol{v}|) = m \] Dabei ist die Masse für jedes Objekt eine charakteristische Konstante, d.h. verschiedene Objekte können verschiedene Massen haben. Entsprechend ist in unserem Beispiel \[ f_0(|\boldsymbol{u}|) = m_0 = 2m \] d.h. die Massen addieren sich.
Der Zusammenhang zwischen Impuls und Geschwindigkeit lautet also \[ \boldsymbol{p} = m \, \boldsymbol{v} \]
Damit haben wir unsere wohlbekannte Formel der Newtonschen Mechanik wiedergefunden! Den Kraftbegriff haben wir dabei gar nicht gebraucht. Allerdings trägt die so gegebene Masse die Einheit Impulseinheit / (Meter/sec) oder abgekürzt IE/(m/s). Wenn wir jedoch zur Impulsmessung als Referenzkörper das sogenannte Urkilogramm verwenden würden, so könnten wir die Einheit Kilogramm (kg) definieren als 1 kg := 1 IE/(m/s). Nach der Impulseinheit freigestellt hätten wir damit 1 IE = 1 kg m/s. Das ist die gewohnte Einheit für den Impuls im sogenannten SI-System der Maßeinheiten.
Fassen wir noch einmal zusammen, welche Zutaten uns zu diesem Ergebnis geführt haben:
Wir wollen noch einen letzten Test machen – gleichsam ein Check, ob wir uns vielleicht irgendwo vertan haben. Ist unser Ergebnis verträglich mit allen anderen Galileitransformationen?
Rechnen wir nach und betrachten den Zusammenstoß von zwei Teilchen. Die Summe der Impulse vor und nach dem Zusammenstoß müssen gleich groß sein, also \[ \boldsymbol{p}_1 + \boldsymbol{p}_2 = \boldsymbol{p}'_1 + \boldsymbol{p}'_2 \] Mit \( \boldsymbol{p} = m \boldsymbol{v} \) folgt \[ m_1 \boldsymbol{v}_1 + m_2 \boldsymbol{v}_2 = m_1 \boldsymbol{v}'_1 + m_2 \boldsymbol{v}'_2 \]
Wir wenden die lineare Abbildung \(R\) auf die Gleichung an und addieren den Term \( m_1 \boldsymbol{u} + m_2 \boldsymbol{u} \) auf beiden Seiten der Gleichung. Nun klammern wir noch \( m_1 \) und \( m_2 \) jeweils aus. Das Ergebnis ist die Gleichung \[ \quad \quad m_1 (\boldsymbol{u} + R\boldsymbol{v}_1) + m_2 (\boldsymbol{u} + R\boldsymbol{v}_2) = \] \[ = m_1 (\boldsymbol{u} + R\boldsymbol{v}'_1) + m_2 (\boldsymbol{u} + R\boldsymbol{v}'_2) \] Das ist gerade die Summe der Impulse, nachdem die Galileitransformation auf Raum und Zeit – und damit die Geschwindigkeiten – angewendet wurde. Alle (verallgemeinerten) Galileitransformationen bilden also eine Symmetriegruppe für die Impulserhaltung mit dem Zusammenhang \( \boldsymbol{p} = m \boldsymbol{v} \) zwischen Impuls und Geschwindigkeit.
Wir können noch ein weiteres interessantes Ergebniss ableiten, auf das wir oben schon einmal kurz gestoßen sind. Betrachten wir nochmal den Zerfall eines ruhenden Objektes der Masse \(m_0\) in zwei (diesmal nicht unbedingt gleiche) Objekte mit Massen \(m_1\) und \(m_2\). Wegen \[ \boldsymbol{p}_1 + \boldsymbol{p}_2 = 0 \] folgt \[ m_1 \boldsymbol{v}_1 + m_2 \boldsymbol{v}_2 = m_0 \boldsymbol{0} = 0 \] Nun wenden wir die Galileitransformation an und erhalten \[ m_1 (\boldsymbol{u} + R\boldsymbol{v}_1) + m_2 (\boldsymbol{u} + R\boldsymbol{v}_2) = m_0 \boldsymbol{u} \] Die Terme mit \(\boldsymbol{v}_1\) und \(\boldsymbol{v}_2\) fallen wegen \( m_1 \boldsymbol{v}_1 + m_2 \boldsymbol{v}_2 = 0 \) heraus, so dass das Ergebnis lautet: \[ m_1 \boldsymbol{u} + m_2 \boldsymbol{u} = m_0 \boldsymbol{u} \] Das gilt nur dann für alle \(\boldsymbol{u}\), wenn \[ m_1 + m_2 = m_0 \] gilt.
Die Masse eines Objektes, das in zwei andere Objekte zerfällt (oder das sich aus zwei anderen Objekten bildet), muss also gleich der Summe der Einzelmassen sein. Anders ausgedrückt: die Masse eines Objektes ist gleich der Summe der Massen seiner Bestandteile.
Darf die Masse eines Objektes auch negativ oder Null sein? Unser Ergebnis sagt ja bisher nur aus, dass die Masse konstant sein muss. Die Frage kann nur experimentell entschieden werden. So beobachten wir, dass beim Auseinanderbrechen eines ruhenden Objektes die Bruchstücke immer in entgegengesetzte Richtungen auseinanderfliegen, niemals aber in die gleiche Richtung. Die Massen der Bruchstücke müssen also das gleiche Vorzeichen haben, damit die Impuls-Summe gleich Null sein kann. Wir wollen annehmen, dass sich Objekte beliebig zu anderen Objekten zusammensetzen lassen
Damit folgt, dass die Massen aller Objekte das gleiche Vorzeichen haben. Wir treffen die Konvention, dass alle Massen positiv sein sollen, und nicht negativ.
Wie sieht es mit Masse Null aus? Objekte mit Masse Null machen offenbar wenig Sinn in unserem bisherigen Rahmen. Sie hätten keinen Impuls und wären damit ohne jeden Einfluss auf Stoß- oder Zerfallsvorgänge. Unser bisheriges physikalisches Modell macht im Grunde keine Aussage zu Objekten mit Masse Null. Falls es sie gibt (was der Fall ist, wie wir noch sehen werden), und falls sie Einfluss auf Stoß- und Zerfallsvorgänge haben, so können sie jedenfalls nicht mit diesem Modell beschrieben werden.
Die Ergebnisse, die wir in diesem Abschnitt erhalten haben, sind alle sehr einleuchtend. Ja, fast erscheinen sie uns trivial zu sein. Wie könnte es auch anders sein, fragen wir uns. Wozu der ganze Aufwand?
Doch Vorsicht! Ist das wirklich alles so? Allein das Experiment kann diese Frage entscheiden. Wenn wir also im Experiment eine Abweichung von unseren Ergebnissen \(\boldsymbol{p} = m \boldsymbol{v}\) oder \(m_1 + m_2 = m_0\) feststellen, so muss eine unserer Voraussetzungen falsch sein. Es sei vorweggenommen, dass wir tatsächlich im Experiment bei sehr großen Geschwindigkeiten Abweichungen finden. Was das für Folgen hat, werden wir in einem der nächsten Kapitel genauer untersuchen.
Zunächst wollen wir aber im nächsten Abschnitt die Untersuchung der Galileigruppe noch etwas ausweiten und auf die Begriffe Kraft und Energie eingehen.
© Jörg Resag, www.joerg-resag.de
last modified on 20 June 2023