Wir haben in den letzten Abschnitten die Transformationen der Poincarégruppe kennengelernt. Diese Transformationen sind spezielle affine Abbildungen in Raum und Zeit: \[ f(x) = \Lambda x + d \] mit dem Vierer-Raumzeitvektor \[ x = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} x^0 \\ \boldsymbol{x} \end{pmatrix} \] mit der nullten Komponente \(x^0 = ct\) (die vier Raumzeit-Indices 0 bis 3 schreiben wir wieder oben). Aus der Forderung, dass sich Teilchen, die sich mit Lichtgeschwindigkeit \(c\) bewegen, auch nach der Transformation wieder mit Lichtgeschwindigkeit bewegen sollen, sowie dem Ausschluss von simultatnen Raumzeit-Dehnungen, hatten wir schließlich die Beziehung \[ g(\Lambda x,\Lambda y) = g(x,y) \] an die Matrix \(\Lambda\) für beliebige Vierervektoren \(x\) und \(y\) erhalten. Die Raumzeit-Metrik \(g\) ist dabei definiert durch \[ g(x,y) = x^0 y^0 - \boldsymbol{x} \boldsymbol{y} \] Bei der Herleitung dieser Bedingung haben wir Gebrauch von der Exponentialdarstellung \( \Lambda = e^X \) gemacht und für die Matrizen \(\Lambda\) schließlich die spezielle Darstellung \[ \Lambda = e^X = e^{ \begin{pmatrix} 0 & \boldsymbol{a} \\ \boldsymbol{a} & G \end{pmatrix} } \] mit \(G^T = -G\) gefunden. Dabei wurden reine Raumzeit-Dehnungs-Matrizen der Form Einheitsmatrix mal Parameter (also \( \Lambda = 1 \,a \) mit \(a \gt 0)\) explizit ausgeschlossen.
Es könnte nun jedoch sein, dass wir Matrizen übersehen haben, die zwar die Bedingung \(g(\Lambda x, \Lambda y) = g(x,y)\) erfüllen, die sich aber nicht in Form einer Exponentialdarstellung schreiben lassen. Gibt es solche Matrizen, und wenn ja, gehören auch diese Matrizen zu den Symmetrietransformationen der Natur?
Zunächst zur Frage: gibt es solche Matrizen? Die Antwort ist einfach: ja, es gibt sie. Ein Beispiel ist die Matrix, die die Raumkoordinaten nicht verändert, aber die das Vorzeichen der Zeitkomponente umdreht. Man bezeichnet diese Abbildung auch als Zeitspiegelung. Die Matrix hat also die Form einer Einheitsmatrix, bei der die Zeit-Zeit-Komponente \(-1\) ist. Lässt man diese Matrix auf Raum und Zeit wirken, so wird aus einem physikalischen Vorgang ein neuer Vorgang, der so aussieht, als würde man den Film rückwärts laufen lassen.
Ist die Zeitspiegelung eine physikalische Symmetrietransformation? Das hängt davon ab, ob der neue Vorgang ebenfalls physikalisch möglich ist. Wir wollen die Beantwortung dieser Frage auf spätere Kapitel verschieben.
Es wäre sicher hilfreich, sich einen Überblick über die Menge aller Matrizen \(\Lambda\) zu verschaffen, die die Bedingung \(g(\Lambda x,\Lambda y) = g(x,y)\) erfüllen. Welche davon lassen sich in Exponentialdarstellung schreiben, und was ist mit den anderen Matrizen los?
Um diese Frage zu beantworten, muss man einigen mathematischen Aufwand treiben. Dies wollen wir hier nicht im Detail tun, und ich möchte den interessierten Leser auf die im Anhang aufgeführte Literatur verweisen. Wir wollen uns im Folgenden auf die wesentlichen Ergebnisse beschränken.
Als erstes kann man zeigen, dass für die Matrizen unserer Gruppe gilt: Diejenigen Matrizen, die sich in der Form \( \Lambda = e^X\) schreiben lassen, bilden die Zusammenhangskomponente, die die Einheitsmatrix \(1\) enthält. Dabei bedeutet Zusammenhangskomponente mit der Einheitsmatrix: Man beginnt mit der Einheitsmatrix und verändert die Matrixelemente stetig, sodass die Matrix jederzeit ein Element der Gruppe bleibt. Diejenigen Gruppen-Matrizen, die sich auf diese Art durch "stetiges Verformen" aus der Einheitsmatrix erzeugen lassen, lassen sich also zugleich in der Exponentialdarstellung schreiben.
Man kann nun zeigen, dass die Gruppe der Matrizen \(\Lambda\), die \( g(\Lambda x, \Lambda y) = g(x,y) \) erfüllen, in vier Zusammenhangskomponenten zerfällt. Diese Zusammenhangskomponenten unterscheiden sich einmal durch das Vorzeichen der Zeit-Zeit-Komponente und zun Anderen durch das Vorzeichen der Determinante der Matrix. Anders ausgedrückt: die erste Zusammenhangskomponente enthält die Einheitsmatrix \(1\), die zweite die Zeitspiegelung \(T\), die dritte die Raumspiegelung \(P\) und die vierte sowohl Raum- als auch Zeitspiegelung, also die Matrix \(P T\). Die Matrizen der einzelnen Komponenten sind dann von der Form \(e^X\) oder \(T \, e^X\) oder \(P \, e^X\) oder \(P T \, e^X\). Ob Raum- und Zeitspiegelung zu den Symmetrietransformationen der Natur gehören, muss man experimentell entscheiden. Es zeigt sich, dass das in der Natur zwar oft, aber nicht immer der Fall ist!
Soviel zum Thema Zusammenhangskomponenten.
An dieser Stelle noch eine kurze Zwischenbemerkung: Die Behauptung, dass bei einer Lie-Gruppe das Bild der Exponentialfunktion stets mit der Zusammenhangskomponente der Eins übereinstimmt, ist nicht generell wahr. Herr Prof. Dr. Hans-Peter Heinz von der Johannes Gutenberg-Universität Mainz war so nett, mich auf dieses interessante Detail hinzuweisen. Seine Begründung, die ich hier einfach mal ohne weitere Kommentare weitergeben möchte, lautet folgendermaßen:
Die Gruppen, die in der Physik normalerweise vorkommen, sind von diesem Einwand nicht betroffen – beispielsweise ist für alle kompakten zusammenhängenden Lie-Gruppen die Exponentialfunktion surjektiv, was aus den Hauptsätzen über maximale Tori folgt. Aber exotisch sind die Gegenbeispiele auch nicht – so ist schon für \(SL(2,\mathbb{R})\) die Exponentialfunktion nicht surjektiv, obwohl die Gruppe zusammenhängend ist (Begründung wie oben!)
Meinen herzlichen Dank nochmal für diesen Hinweis!
Es gibt einen weiteren wichtigen Satz, der eine allgemeine Lorentzmatrix in Beziehung zu den speziellen Transformationen Boost und Drehung aus den letzten Abschnitten setzt. Man kann nämlich jede Lorentzmatrix \(\Lambda\), die zur Zusammenhangskomponente der Einheitsmatrix gehört (d.h. \(\Lambda = e^X\)) in der Form \[ \Lambda = \Lambda_{r1} \, \Lambda_b \, \Lambda_{r2} \] schreiben. Dabei sind \(\Lambda_{r1}\) und \(\Lambda_{r2}\) Drehungen im Raum und \(\Lambda_b\) ist ein Boost (vgl. die letzten beiden Abschnitte). Man kann also eine beliebige Lorentztransformation immer durch eine geeignete Drehung, einen anschließenden Boost und noch eine Drehung ersetzen.
Es noch eine zweite Möglichkeit, eine Lorentztransformation in Boosts und ein weiteres Element zu zerlegen. Sie ist für die allgemeine Darstellungstheorie der Poincarégruppe in der Quantentheorie von zentraler Bedeutung, und wir wollen daher kurz darauf eingehen:
Zunächst einmal geben wir zwei Vierervektoren \(p\) und \(P\) vor, wobei \(g(p,p) = g(P,P)\) gelten soll. Wir müssen diese Vektoren noch nicht physikalisch interpretieren. Da man jedoch sehr oft die folgende Argumentation auf Impulsvektoren anwendet, haben wir die Bezeichnungsweise schon mal vorsorglich entsprechend angepasst.
Wir ordnen nun diesen beiden Vektoren einen Boost \(\Lambda_b(p,P)\) zu, der den Vektor \(p\) auf \(P\) abbildet: \[ [\Lambda_b(p,P)] \,p = P \] Man kann mit Hilfe unserer Darstellung für Boost-Matrizen aus den letzten Abschnitten zeigen, dass man immer einen entsprechenden Boost finden kann, und dass dieser Boost eindeutig durch die beiden Vektoren festgelegt ist.
Nun betrachten wir eine beliebige Lorentz-Transformation \(\Lambda\) und lassen sie auf den Vektor \(p\) wirken, der dadurch zum Vektor \(\Lambda p\) wird. Die beiden Vektoren \(\Lambda p\) und \(P\) legen nun ebenfalls eindeutig einen Boost \(\Lambda_b(\Lambda p,P)\) fest. Es gilt also \[ [\Lambda_b(\Lambda p,P)] \, \Lambda p = P \] Wir definieren nun eine Lorentzmatrix \( \Lambda_l(\Lambda,p,P)\) (der Index ist der Buchstabe \(l\), nicht die Zahl \(1\)) als \[ \Lambda_l(\Lambda,p,P) := [\Lambda_b(\Lambda p,P)] \, \Lambda \, [\Lambda_b(p,P)]^{-1} \] Die Definition dieser Matrix ist nichts anderes als die Festlegung einer Zerlegung für \(\Lambda\), denn wir können die Gleichung auch nach \(\Lambda\) auflösen: \[ \Lambda = [\Lambda_b(\Lambda p,P)]^{-1} \, [\Lambda_l(\Lambda,p,P)] \, [\Lambda_b(p,P)] \] Diese Zerlegung für \(\Lambda\) ist durch die Wahl der Vektoren \(p\) und \(P\) (mit \(g(p,p) = g(P,P)\) ) eindeutig festgelegt. Sie ist immer dann nützlich, wenn man sich fragt, was mit einem Vektor \(p\) durch irgendwelche beliebigen Lorentztransformationen so passieren kann. Dabei wird man sich dann einen für die Untersuchung geeigneten Vektor \(P\), der die gleiche Raumzeit-Metrik wie \(p\) hat, aussuchen. Beispielsweise kann man bei massiven Teilchen den Vierervektor \(P = (mc, \boldsymbol{0})\) nehmen, sodass die Matrix \([\Lambda_b(p,P)]\) das Teilchen in dessen Ruhesystem boostet. Bei masselosen Teilchen muss man \(P\) dagegen anders wählen, da sie kein Ruhesystem haben.
Wirklich wichtig wird diese Zerlegung jedoch erst im Rahmen der Darstellungstheorie der Poincarégruppe (der Begriff der Darstellung einer Gruppe wird uns in späteren Kapiteln noch begegnen).
Die neue Matrix \( \Lambda_l(\Lambda,p,P)\) hat nun eine interessante Eigenschaft: sie verändert den Vektor \(P\) nicht, denn es ist \[ [\Lambda_l(\Lambda,p,P)] \, P = \] \[ = [\Lambda_b(\Lambda p,P)] \, \Lambda \, [\Lambda_b(p,P)]^{-1} \,P = \] \[ = [\Lambda_b(\Lambda p,P)] \, \Lambda p = P \] Man bezeichnet die Gruppe der Lorentzmatrizen mit dieser Eigenschaft als die zum Vektor \(P\) gehörende kleine Gruppe (engl.: little group) oder auch als die Isotropiegruppe oder stabile Untergruppe zu \(P\). Dies erklärt den Index \(l\), der für litte steht.
Was tut nun die Zerlegung \[ \Lambda = [\Lambda_b(\Lambda p,P)]^{-1} \, [\Lambda_l(\Lambda,p,P)] \, [\Lambda_b(p,P)] \] anschaulich mit dem Vektor \(p\)? Sie macht über einen Boost (also eine Geschwindigkeitstransformation) daraus erst einmal den Vektor \(P\), führt dann eine Lorentztransformation aus, die diesen Vektor nicht ändert, und sorgt dann über einen weiteren Boost dafür, dass aus \(P\) der Vektor \(\Lambda p\) wird.
Bleibt die Frage: was bedeuten diese Transformationen \(\Lambda_l(\Lambda,p,P)\) aus der kleinen Gruppe, die den Vektor \(P\) nicht ändern, anschaulich?
Es zeigt sich, dass man mehrere Fälle unterscheiden muss (vgl. z.B. das Buch von Sexl und Urbantke aus dem Anhang). Wir wollen hier nur auf die wichtigsten beiden Fälle eingehen:
Zum Schluss noch eine Bemerkung zur Topologie der Lorentzgruppe. Was ist damit gemeint?
Die Matrizen der Lorentzgruppe haben 16 reelle Komponenten. Man kann sie daher auch als 16-dimensionale Vektoren auffassen. Die Bedingung \(g(\Lambda x,\Lambda y) = g(x,y)\) führt jedoch dazu, dass diese 16 Komponenten nicht mehr unabhängig voneinander sind. Sie können als stetige Funktionen von nur 6 reellen Parametern geschrieben werden (drei Drehwinkel und drei Boost-Parameter, vgl. die vorherigen drei Abschnitte; zusätzlich braucht man noch eine Angabe darüber, auf welcher Zusammenhangskomponente der Vektor liegen soll).
Die Vektoren liegen also auf 6-dimensionalen Unterräumen eines 16-dimensionalen Raums. Die 6 Parameter kann man als Koordinaten auf diesen Unterräumen auffassen. Wie wir oben gesehen haben, gibt es genau vier verschiedene Unterräume, die nicht miteinander verbunden sind. Wir haben diese Unterräume oben als Zusammenhangskomponenten bezeichnet.
Man kann sich nun fragen, welche Form diese Unterräume haben. Was passiert beispielsweise, wenn ich eine geschlossene Kurve auf einem dieser Unterräume betrachte und versuche, diese Kurve langsam und stetig immer kleiner zu machen und sie schließlich zu einem einzigen Punkt zusammenzuziehen? Geht das für jede geschlossene Kurve?
Diese Frage soll hier nicht in voller Allgemeinheit untersucht werden. Den interessanten Kern der Sache kann man aber recht einfach an den Drehungen erkennen. Die Tatsache, dass Drehungen zu den Lorentztransformationen dazugehören, bewirkt, dass es zwei verschiedene Sorten von geschlossenen Kurven gibt. Die einen kann man stetig zu einem Punkt zusammenziehen, und die anderen nicht. Um das zu verstehen, schauen wir uns noch einmal die Darstellung einer Drehung an (vgl. vorigen Abschnitt). Eine Drehung wirkt auf einen räumlichen Vektor \(\boldsymbol{x}\) nach der Formel \[ e^{\,\omega A} \boldsymbol{x} = \] \[ = - ( \cos{\omega}) \, [(\boldsymbol{e} \boldsymbol{x}) \boldsymbol{e} - \boldsymbol{x}] + (\boldsymbol{e} \boldsymbol{x}) \boldsymbol{e} + \] \[ + (\sin{\omega}) \, (\boldsymbol{e} \times \boldsymbol{x}) \] wobei \[ A \, \boldsymbol{x} = \boldsymbol{e} \times \boldsymbol{x} \] ist. Dabei gibt der Einheitsvektor \(\boldsymbol{e}\) die Drehachse und \(\omega\) den Drehwinkel an. Wir können Drehachse und Drehwinkel auch zu einem Vektor zusammenfassen: \[ \boldsymbol{w} = \omega \boldsymbol{e} \] Dieser Vektor gibt die drei Parameter jeder Drehung vollständig an, d.h. zu jedem Vektor \(\boldsymbol{w}\) gibt es eine Drehung.
Gibt es umgekehrt zu jeder Drehung nur genau einen eindeutigen Vektor \(\boldsymbol{w}\)? Das ist nicht der Fall! Messen wir den Drehwinkel im Bogenmaß, so gehören z.B. die beiden Vektoren \begin{align} \boldsymbol{w}_1 &= \; \; \pi \boldsymbol{e} \\ \boldsymbol{w}_2 &= - \pi \boldsymbol{e} \end{align} zur selben Drehung. Im ersten Fall haben wir eine halbe Drehung in der einen Drehrichtung, im anderen Fall eine halbe Drehung in der entgegengesetzten Drehrichtung vor uns. Beide Drehungen sind identisch! Genauso verhält es sich mit den beiden Vektoren \begin{align} \boldsymbol{w}_1 &= \; \; \frac{\pi}{2} \boldsymbol{e} \\ \boldsymbol{w}_2 &= - \frac{3\pi}{2} \boldsymbol{e} \end{align} die einer Viereldrehung linksherum bzw. einer Dreivierteldrehung rechtsherum entsprechen.
Wir wollen versuchen, den Parameterraum so einzuschränken, dass möglichst zu jeder Drehung
genau ein Vektor \(\boldsymbol{w}\) gehört. Das lässt sich durch die Bedingung
\( \omega = |\boldsymbol{w}| \le \pi\)
weitgehend erreichen.
Jeder Vektor \(\boldsymbol{w}\) mit
\( \omega = |\boldsymbol{w}| \lt \pi\)
gehört nun eindeutig
zu genau einer Drehung. Lediglich für \( \omega = |\boldsymbol{w}| = \pi\)
gibt es nach wie vor zwei Vektoren, die zu einer halben Drehung gehören:
die beiden Vektoren
\(\boldsymbol{w}_1 = \pi \boldsymbol{e}\) und
\(\boldsymbol{w}_2 = - \pi \boldsymbol{e}\).
Der Parameterraum der Vektoren \(\boldsymbol{w}\)
mit \( \omega = |\boldsymbol{w}| \le \pi\) sieht also aus wie eine Vollkugel vom
Radius \(\pi\), bei dem einander gegenüberliegende Punkte auf der Kugeloberfläche
miteinander identifiziert werden müssen, denn
\(\boldsymbol{w}_1 = \pi \boldsymbol{e}\) und
\(\boldsymbol{w}_2 = - \pi \boldsymbol{e}\) sind ein-und-dieselbe Drehung:

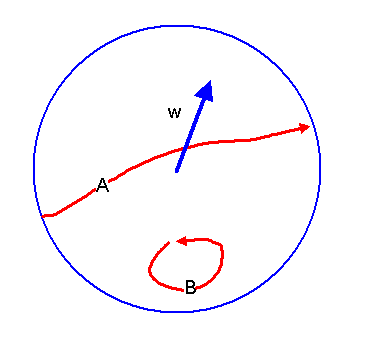
In diesem Parameterraum gibt es nun eine Sorte geschlossener Kurven, die sich auf einen Punkt zusammenziehen lassen. Diese Kurven liegen im Inneren der Kugel und berühren die Kugeloberfläche nicht. Eine solche Kurve ist in der obigen Grafik als Kurve \(B\) eingezeichnet.
Es gibt aber noch eine zweite Sorte geschlossener Kurven (siehe Kurve \(A\) in der obigen Grafik).
Diese Kurven stoßen an einem Punkt
durch die Kugeloberfläche und treten an dem gegenüberliegenden Punkt wieder in die Kugel ein.
Da die beiden gegenüberliegenden Punkte auf der Kugeloberfläche zu einer einzigen
Drehung gehören, ist auch dies eine geschlossene Kurve im Raum der Drehungen.
Diese Kurve lässt sich nicht auf einen Punkt zusammenziehen!
Man sagt deshalb auch, die Drehgruppe und damit die Lorentzgruppe ist
nicht einfach zusammenhängend.
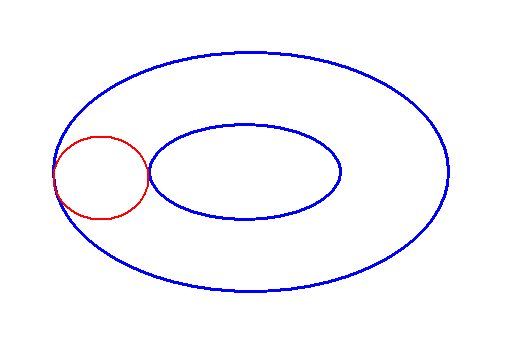
Bei einem Torus
(also einer Ringoberfläche oder einem Donut) ist das ganz ähnlich.
Auch dort gibt es geschlossene Kurven, die sich nicht zu
einem Punkt zusammenziehen lassen.
Das folgende Bild zeigt eine solche Kurve auf einem Torus:
Dass Drehgruppe und damit Lorentzgruppe nicht einfach zusammenhängend sind, hat Folgen: Will man die Drehung von quantenmechanischen Zuständen beschreiben, so muss man zu einer einfach zusammenhängenden Gruppe übergehen: der universelle Überlagerungsgruppe. Mehr dazu siehe später in Kapitel 4.6 Darstellung von Symmetrien in der Quantentheorie und in Kapitel 4.8 Drehungen, Spin und Drehimpuls.
© Jörg Resag, www.joerg-resag.de
last modified on 28 June 2023