

Im letzten Kapitel haben wir zu den Drehungen und den Raum-Zeit-Translationen die nichtrelativistischen Boosts als Symmetrieoperationen hinzugenommen, was uns zur Galileigruppe und ihren Darstellungen geführt hat. Nun wissen wir aber, dass nichtrelativistische Boosts nur bei kleinen Boostgeschwindigkeiten eine näherungsweise Symmetrie der Raumzeit sind. Die korrekten Symmetrieoperationen sind die relativistischen Boosts, wie wir sie in Kapitel 3.3 bereits kennengelernt haben. Zusammen mit den Drehungen und den Raum-Zeit-Translationen bilden sie die Poincarégruppe (siehe Kapitel 3.1 und Folgende). Lässt man die Raum-Zeit-Translationen weg, spricht man von der Lorentzgruppe. Genau genommen gehören zu dieser Gruppe noch die Raum- und Zeitspiegelungen hinzu. Diese werden wir jedoch in diesem Kapitel nicht weiter betrachten. Wenn also im Folgenden von der Lorentzgruppe und der Poincarégruppe die Rede ist, dann sind Raum- und Zeitspiegelungen immer ausgenommen.
Das vorliegende Kapitel ist recht umfangreich, obwohl ich versucht habe, mich auf die wichtigsten Aspekte zu beschränken. Daran sieht man, dass man leicht ganze Bücher über die Darstellungstheorie der Poincarégruppe schreiben kann. Wer sich aber die Mühe macht, dieses Kapitel genauer durchzugehen, der hat in den nächsten Kapiteln die Chance, Pauli- und Diracmatrizen wowie Klein-Gordon- und Diracgleichung in einem etwas anderen und umfassenderen Sinn kennenzulernen, als man dies normalerweise in Physikvorlesungen tun kann.
Zunächst eine kurze Wiederholung von Kapitel 3.3. Die Notation erfolgt diesmal in natürlichen Einheiten, d.h. \(\hbar = 1\) und \(c = 1\) in den Formeln – Geschwindigkeiten werden also relativ zur Lichtgeschwindigkeit angegeben, Zeiten werden durch die Strecke repräsentiert, die das Licht in dieser Zeit zurücklegt, und Wirkungen werden relativ zu \(\hbar\) angegeben.
|
relativistische Boosts: Relativistische Boosts \(\Lambda_b\) bilden einen Raumzeitvektor \( x = (t, \boldsymbol{x}) \) auf den Vektor \( \Lambda_b \, x \) ab. Dabei ist \(\Lambda_b\) eine reelle symmetrische 4-mal-4-Matrix, die die folgenden Block-Darstellungen hat: \[ \Lambda_b = e^{ \begin{pmatrix} 0 & \boldsymbol{\alpha} \\ \boldsymbol{\alpha} & 0 \end{pmatrix} } = \] \[ = \begin{pmatrix} (\cosh{\alpha}) & (\sinh{\alpha}) \, \boldsymbol{e} \\ (\sinh{\alpha}) \, \boldsymbol{e} & \mathbb{1} + (\cosh{\alpha} - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} = \] \[ = \begin{pmatrix} \gamma & \gamma \boldsymbol{u} \\ \gamma \boldsymbol{u} & \mathbb{1} + (\gamma - 1) \, (\boldsymbol{e} \, \boldsymbol{e}^T) \end{pmatrix} \] mit der Rapidität \( \alpha \) , also \[ \boldsymbol{\alpha} = \alpha \boldsymbol{e} \] mit \( |\boldsymbol{e}| = 1 \) (in Kapitel Kapitel 3.3 hatten wir die Bezeichnung \(\boldsymbol{a}\) statt \(\boldsymbol{\alpha}\) verwendet, aber \(\boldsymbol{a}\) wollen wir hier für den räumlichen Translationsvektor verwenden). Weiter ist \[ \gamma := \cosh{\alpha} \] der Lorentzfaktor sowie \[ \boldsymbol{u} = |\boldsymbol{u}| \, \boldsymbol{e} \] die Boostgeschwindigkeit mit \[ \boldsymbol{u} = \frac{\sinh{\alpha}}{\cosh{\alpha}} \, \boldsymbol{e} \] Nützlich sind noch die Formeln \[ \boldsymbol{u} = \sqrt{ 1 - \frac{1}{\gamma^2} } \, \boldsymbol{e} \] \[ \gamma = \sqrt{ \frac{1}{1 - \boldsymbol{u}^2} } \] \[ \gamma \boldsymbol{u} = (\sinh{\alpha}) \, \boldsymbol{e} \] \[ (\cosh{\alpha})^2 - (\sinh{\alpha})^2 = 1 \] Es folgt, dass der Betrag der Boostgeschwindigkeit \(\boldsymbol{u}\) in natürlichen Einheiten immer kleiner-gleich Eins sein muss, d.h. die maximal erreichbare Boostgeschwindigkeit ist die Lichtgeschwindigkeit. Führt man hintereinander zwei Boosts in derselben Richtung, so entspricht das nicht einem Boost mit der Summe dieser Boostgeschwindigkeit. Die Boostgeschwindigkeiten addieren sich in diesem Sinn also nicht! Das ist bei den nichtrelativistischen Boosts anders. Will man einen additiven Parameter haben, so muss man die Rapidität \(\alpha\) verwenden. Führt man hintereinander zwei Boosts in derselben Richtung aus, so entspricht das einem Boost mit der Summe dieser Rapiditäten. Im diesem Sinn sowie im Sinn der Exponentialdarstellung ist daher die Rapidität bzw. der Rapiditätsvektor \(\boldsymbol{\alpha}\) die natürliche Parameterwahl! |
Zur Schreibweise der Generatoren in diesem Kapitel:
Für die Generatoren der Drehgruppe werden wir \[ A(J_k) = - A_k \] schreiben, so dass \[ R(\boldsymbol{w}) = e^{- i \boldsymbol{w} A(\boldsymbol{J})} \] ist. Beim Übergang zu den unitären Darstellungsoperatoren müssen wir dann nur noch \(\hat{\boldsymbol{J}}\) statt \(A(\boldsymbol{J})\) schreiben. Vergleich mit der Schreibweise in Kapitel 4.8 ergibt \[ - i \boldsymbol{w} \, A(\boldsymbol{J}) \, \boldsymbol{x} = G(\boldsymbol{w}) \, \boldsymbol{x} = \] \[ = \boldsymbol{w} \times \boldsymbol{x} \] also auch \[ - i \boldsymbol{e}_k \, A(\boldsymbol{J}) \, \boldsymbol{x} = - i A(J_k) \, \boldsymbol{x} = \] \[ = G(\boldsymbol{e}_k) \, \boldsymbol{x} = \boldsymbol{e}_k \times \boldsymbol{x} \] Diese Gleichung brauchen wir etwas weiter unten für den Kommutator zweier Boostgeneratoren.
Bei Boosts schreiben wir analog zum vorherigen Kapitel \[ \Lambda_b = e^{i \boldsymbol{\alpha} A(\boldsymbol{K})} \] wobei statt der Boostgeschwindigkeit hier die Rapidität als Parametervektor verwendet wird.
Bei den Drehungen war die reelle Matrix im Exponenten antisymmetrisch. Für die Generatoren bedeutete das: \[ i A(J_k)^T = - i A(J_k) \] Komplexes Konjugieren ergibt \[ (i A(J_k)^T)^* = - (i A(J_k))^* \] Da \( (i A(J_k)) \) reell ist, können wir rechts den Stern wieder weglassen. Links dagegen verwenden wir \[ (i A(J_k)^T)^* = - i (A(J_k)^T)^* = \] \[ = - i A(J_k)^+ \] Linke und rechte Seite zusammen ergeben also \[ - i A(J_k)^+ = - i A(J_k) \] und somit \[ A(J_k)^+ = A(J_k) \] Die Generatoren der Drehgruppe sind also hermitesche Matrizen. Genau darin lag der Sinn, den Faktor \(i\) herauszuziehen. Beim Übergang zur Quantentheorie werden aus den Matrizen hermitesche Operatoren, so dass man eine unitäre Darstellung der Überlagerungsgruppe erhält. Da die Gruppe kompakt ist, liefern die unitären Darstellungen zugleich sämtliche möglichen Matrixdarstellungen.
Bei den Boosts ist die Matrix im Exponenten nun symmetrisch: \[ i A(K_k) = \begin{pmatrix} 0 & \boldsymbol{e}_k \\ \boldsymbol{e}_k & 0 \end{pmatrix} \] Daher ergibt sich für die Generatoren der Boosts die Beziehung \[ A(K_k)^+ = - A(K_k) \] d.h. die Generatoren der Boosts sind anti-hermitesche Matrizen.
Schauen wir uns die Kommutatoren der Boost-Generatoren an: \[ [i A(K_i) , i A(K_j)] = \begin{pmatrix} 0 & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{e}_i \boldsymbol{e}_j^T - \boldsymbol{e}_j \boldsymbol{e}_i^T \end{pmatrix} \] Offenbar wirkt der Kommutator nur auf die räumlichen Komponenten, so dass wir kurz schreiben: \[ [i A(K_i) , i A(K_j)] \, \boldsymbol{x} = \] \[ = (\boldsymbol{e}_i \boldsymbol{e}_j^T - \boldsymbol{e}_j \boldsymbol{e}_i^T) \, \boldsymbol{x} = \] \[ = \boldsymbol{e}_i x^j - \boldsymbol{e}_j x^i \] wobei wir die Indizes der Raumkomponenten \(x^i\) wieder oben schreiben. Es ist interessant, dass der Kommutator der Boost-Generatoren nicht gleich Null ist, anders als im nichtrelativistischen Fall. Um den Ausdruck rechts besser verstehen zu können, schauen wir uns zum Vergleich den folgenden Ausdruck an (mit Summen über doppelte Indices): \[ \epsilon_{ijk} \, (- i) \, A(J_k) \, \boldsymbol{x} = \] \[ = \epsilon_{ijk} \, G(\boldsymbol{e}_k) \, \boldsymbol{x} = \] \[ = \epsilon_{ijk} \, \boldsymbol{e}_k \times \boldsymbol{x} = \] \[ = \epsilon_{ijk} \, \boldsymbol{e}_k \times \boldsymbol{e}_l \, x^l = \] \[ = \epsilon_{ijk} \, \epsilon_{klm} \, \boldsymbol{e}_m \, x^l = \] \[ = (\delta_{il} \, \delta_{jm} - \delta_{im} \, \delta_{jl}) \, \boldsymbol{e}_m x^l = \] \[ = \boldsymbol{e}_j \, x^i - \boldsymbol{e}_i \, x^j = \] \[ = - [i A(K_i) , i A(K_j)] \boldsymbol{x} = \] \[ = [A(K_i) , A(K_j)] \boldsymbol{x} \] Damit haben wir unser Ergebnis:
| Kommutator der Boost-Generatoren: \[ [A(K_i) , A(K_j)] = - i \epsilon_{ijk} \, A(J_k) \] |
Das Vertauschen von Boosts in verschiedenen Richtungen hat also etwas mit Drehungen zu tun! Der Kommutator zweier Boostgeneratoren sieht fast genauso aus wie der Kommutator zweier Drehgeneratoren (siehe Kapitel 4.8) \[ [A(J_i) , A(J_j)] = i \epsilon_{ijk} \, A(J_k) \] mit einem wichtigen Unterschied: das Vorzeichen!
Man kann nun weiter zeigen, dass sich \(A(\boldsymbol{K})\) bei Drehungen wie ein Vektor verhält. Das war schon bei der Galileigruppe so. Also haben wir: \[ [A(J_i) , A(K_j)] = i \epsilon_{ijk} \, A(K_k) \] Damit ist die Lie-Algebra der Lorentzgruppe bereits komplett. Hinzu kommen noch die Kommutatoren mit den Generatoren \(A(P^\mu)\) der Raum-Zeit-Translationen. Dass sich \(A(P^\mu)\) wirklich wie ein Vierervektor transformiert, muss man natürlich mit Hilfe der Gruppenstruktur noch nachweisen, was wir weiter unten tun werden.
Man kann nun zeigen, dass die Lie-Algebra dieser Generatoren das Auftreten von Zentralladungen nicht zulässt, anders als bei der Galileigruppe. Die Poincarégruppe ist in dieser Hinsicht einfacher als die Galileigruppe, bei der man sich ständig mit projektiven Phasen herumschlagen muss. Den Beweis findet man z.B. in Steven Weinbergs Buch The Quantum Theory of Fields, Vol. 1, Kapitel 2.7 (Seite 84). Das bedeutet, dass beim Übergang zu quantenmechanischen Darstellungen keine projektiven Phasen mehr auftreten, wenn wir zur einfach-zusammenhängenden Überlagerungsgruppe übergehen.
Schauen wir uns nun also an, wie die Überlagerungsgruppe der Poincarégruppe aussieht. Da für Raum-Zeit-Translationen keine Überlagerung notwendig ist (siehe Kapitel 4.7 ), genügt es, wenn wir uns zunächst mit der Lorentzgruppe beschäftigen und Raum-Zeit-Translationen weglassen. Dabei werden wir feststellen, dass sich viele Ähnlichkeiten zur Drehgruppe ergeben. Außerdem werden wir sehen, dass die Drehungen der Grund dafür sind, dass eine Überlagerungsgruppe notwendig ist (siehe auch Kapitel 4.8 ).
Die Überlagerungsgruppe der Lorentzgruppe lässt sich weitgehend analog zur Überlagerungsgruppe der Drehgruppe konstruieren (siehe Kapitel 4.8 ). Dabei werde ich wie schon bei den Drehungen das Ergebnis einfach angeben – wie man auf dieses Ergebnis kommt, möchte ich erst in einem späteren Kapitel im Zusammenhang mit Clifford-Algebren und Spingruppen diskutieren. Hier ist das Ergebnis:
|
Ausgeschrieben lautet die Matrix \(\sigma(x)\) also: \[ \sigma(x) = \begin{pmatrix} x^0 + x_3 & x_1 - i x_2 \\ x_1 + i x_2 & x^0 - x_3 \end{pmatrix} \] Man rechnet leicht nach, dass wegen \( \det{g} = 1 \) die so definierte Matrix \(\Lambda\) die Minkowskimetrik eines Vierervektors nicht ändert: \[ (\Lambda x)^2 = \] \[ = \det{\sigma(\Lambda x)} = \] \[ = \det{(g \, \sigma(x) \, g^+)} = \] \[ = \det{g} \, \det{\sigma(x)} \, \det{g^+} = \] \[ = \det{\sigma(x)} = \] \[ = x^2 \] Also ist \(\Lambda\) eine Lorentz-Matrix. Dass Raum-Zeit-Spiegelungen ausgeschlossen sind, weist man nach, indem man \(g\) und damit \(\Lambda\) über einen stetigen Weg mit der Einheitsmatrix verbindet. Man kann auch beweisen, dass man tatsächlich jede Lorentz-Matrix \(\Lambda\) aus der Zusammenhangskomponente mit der \(1\) durch ein passendes \(g\) so erreichen kann. Außerdem ist gesichert, dass dem Produkt zweier Gruppenelemente \(g\) und \(g'\) aus \(SL(2,\mathbb{C})\) auch das Produkt der entsprechenden Lorentz-Matrizen zugeordnet wird, d.h. die Gruppenstruktur wird berücksichtigt.
Wie bei den Drehungen ist die Zuordnung von \(SL(2,\mathbb{C})\) zu den Lorentz-Matrizen nicht eindeutig: Den beiden \(SL(2,\mathbb{C})\)-Matrizen \(g\) und \(- g\) wird dieselbe Lorentz-Matrix zugeordnet! Daher ist \(SL(2,\mathbb{C})\) eine Überlagerungsgruppe der Lorentzgruppe (genauer: der Zusammenhangskomponente mit der Eins).
Die Gleichung \(g \, \sigma(x) \, g^+ = \sigma(\Lambda x) \) definiert also eine surjektive Projektion \[ \rho: \, SL(2,\mathbb{C}) \rightarrow SO(1,3) \] die mit der Gruppenstruktur verträglich ist. Dabei haben wir wie üblich für die Zusammenhangskomponente der Lorentzgruppe mit der \(1\) die Bezeichnung \(SO(1,3)\) verwendet. Die Schreibweise \(SO(1,3)\) steht für die reellen 4-mal-4-Matrizen mit Determinante 1 (daher das \(S\) in \(SO(1,3)\) – so werden Raum-Zeit-Spiegelungen ausgeschlossen), die die Metrik mit einer \(+1\) und drei \(-1\)-en in der Diagonale der metrischen Matrix invariant lassen (also unsere bekannte Minkowskimetrik).
Wenn wir die obigen Zeilen mit den Erkenntnissen über die Drehgruppe und ihre Überlagerungsgruppe \(SU(2)\) aus Kapitel 4.8 vergleichen, so stellen wir eine große Ähnlichkeit fest. Tatsächlich habe ich Teile des Textes fast unverändert übernommen und im Wesentlichen \(u \in SU(2)\) durch \(g \in SL(2,\mathbb{C})\) sowie \(\sigma(\boldsymbol{x})\) durch \(\sigma(x)\) und die Drehmatrix \(R\) durch die Lorentzmatrix \(\Lambda\) ersetzt. Warum geht das?
Schauen wir uns dazu die Matrix \(g \in SL(2,\mathbb{C})\) an: Sie enthält 4 komplexe Matrixelemente. Die Bedingung Determinante gleich Eins bewirkt, dass nur drei dieser Matrixelemente unabhängig sind. Das entspricht 6 reellen Parametern. So muss es auch sein, denn die zu \(g\) gehörende Lorentzmatrix \(\Lambda\) hängt ebenfalls von 6 reellen Parametern ab (drei Drehwinkel und drei Boostparameter).
Man kann nun jede beliebige invertierbare komplexe Matrix \(g\) nach dem Polar Decomposition Theorem ( Polarzerlegungs-Satz) in eindeutiger Weise in eine unitäre Matrix \(u\) und eine exponentierte hermitesche Matrix \(h\) aufteilen:
| Polarzerlegung: \[ g = u \, e^h \] mit \[ u^+ u = 1 \] und \[ h^+ = h \] |
(man kann auch \( g = e^{h'} u' \) schreiben, wobei aber \(e^{h'}\) und \(u'\) andere Matrizen mit derselben Determinante wie \(e^h\) und \(u\) sind).
Die obige Polarzerlegung ist das Matrix-Analogon zur Zerlegung einer komplexen Zahl \(z\) in ihren Betrag und eine Phase: \[ z = e^{i \varphi} \, |z| \] wobei \(e^{i \varphi}\) der unitären Matrix \(u\) und \(|z|\) der Matrix \(e^h\) entspricht. Nun ist die Determinante von \(g\) gerade eine solche komplexe Zahl \(z\), also gilt \[ \det{g} = e^{i \varphi} \, |\det{g}| \] Man kann sich nun überlegen, dass \(e^{i \varphi}\) gerade gleich \( \det{u} \) ist, und dass \( |\det{g}| \) gerade gleich \( \det{e^h} \) ist (kurze Begründung: die Determinante ist das Produkt der Eigenwerte, und die sind bei \(u\) komplexe Phasen, während sie bei \(e^h\) positive reelle Zahlen sind). Also: \[ \det{g} = \] \[ = \det{u} \, \det{e^h} = \] \[ = e^{i \varphi} \, |\det{g}| \] mit \( \det{u} = e^{i \varphi} \) und \( \det{e^h} = |\det{g}| \).
Wir verlangen jetzt, dass \(g \in SL(2,\mathbb{C})\) ist, d.h. wir verlangen die Zusatzbedingung \( \det{g} = 1 \). Aus den obigen Formeln folgt sofort \[ \det{u} = 1 \] d.h. \( u \in SU(2)\).
Für die andere Matrix \( e^h \) folgt \[ \det{e^h} = 1 \] und mit der Formel \( \det{e^h} = e^{\mathrm{Spur} \, h} \) folgt \[ \mathrm{Spur} \, h = 0 \] Was bedeutet das für unsere Formel \[ g \, \sigma(x) \, g^+ = \sigma(\Lambda x) \] Da diese Formel die Gruppenstruktur respektiert, folgt für \( g = u \, e^h \) die Formel \[ (u e^h) \, \sigma(x) \, (u e^h)^+ = \sigma(\Lambda_u \Lambda_b x) \] mit \[ u \, \sigma(x) \, u^+ =: \sigma(\Lambda_u x) \] und \[ e^h \, \sigma(x) \, e^h =: \sigma(\Lambda_b x) \] Zeigen wir nun, dass \(\Lambda_u\) eine Drehung und \(\Lambda_b\) ein Boost ist: \[ u \, \sigma(x) \, u^+ = \] \[ = u \, (x^0 \, 1) \, u^+ + u \, \sigma(\boldsymbol{x}) \, u^+ = \] \[ = x^0 + u \, \sigma(\boldsymbol{x}) \, u^+ = \] \[ = x^0 + \sigma(R \boldsymbol{x}) = \] \[ = \sigma(\Lambda_u x) \] Dabei haben wir aus Kapitel 4.8 die Formel \( u \, \sigma(\boldsymbol{x}) \, u^+ = \sigma(R \boldsymbol{x}) \) verwendet, die jeder \(SU(2)\)-Matrix \(u\) eine Drehmatrix \(R\) zuordnet. Man sieht nun, wie diese Formel wunderbar in unser Konzept für die Lorentz-Transformationen hineinpasst und wie sie in diesem erweiterten Formalismus aufgeht. Die Matrix \(\Lambda_u\) dreht also die räumlichen Komponenten von \(x\) und lässt die Zeitkomponente \( x^0 = t \) unverändert – sie ist also eine Lorentz-Drehmatrix. Aus Kapitel 4.8 wissen wir, dass wir schreiben können:
| Drehung: \[ u = e^{-\frac{i}{2} \, \sigma(\boldsymbol{w})} = \] \[ = 1 \, \cos{\frac{\omega}{2}} - i \, \sigma(\boldsymbol{e}) \, \sin{\frac{\omega}{2}} \] |
mit \( \boldsymbol{w} = \omega \boldsymbol{e} \), d.h. \( \omega = |\boldsymbol{w}| \) und \( \boldsymbol{e} = \boldsymbol{w} / |\boldsymbol{w}| \).
Nun zu \[ e^h \, \sigma(x) e^h =: \sigma(\Lambda_b x) \] Da \(h\) eine hermitesche spurlose Matrix ist, können wir sie mit Hilfe der drei Paulimatrizen und dreier reeller Parameter \(\boldsymbol{\alpha} = (\alpha^i)\) schreiben als \[ h = \frac{1}{2} \sigma(\boldsymbol{\alpha}) \] Den Faktor \(\frac{1}{2}\) haben wir herausgezogen, damit \(\boldsymbol{\alpha}\) später wieder die Bedeutung der Rapidität erhält. Man kann die Exponentialreihe nun wieder explizit aufsummieren (siehe z.B. Kapitel 6 im Skript zur Vorlesung Quantentheorie II von Prof. Schütte im SS 1992 (ITKP, Uni Bonn), Schwerpunkt: die Poincaré-Gruppe, Poincaréskript (.ps, 807kb) ) und erhält:
| Boost: \[ e^h = e^{\frac{1}{2} \sigma(\boldsymbol{\alpha})} = \] \[ = 1 \, \cosh{\frac{\alpha}{2}} + \sigma(\boldsymbol{e}) \, \sinh{\frac{\alpha}{2}} \] |
mit \(\boldsymbol{\alpha} = \alpha \boldsymbol{e} \) und \( |\boldsymbol{e}| = 1 \).
Diese Formel sieht sehr ähnlich zu der Formel für \(u\) oben aus, und tatsächlich kann man sie auch aus der Formel für \(u\) durch analytische Fortsetzung erhalten, indem man \( \omega = i \alpha \) einsetzt und \( \cos{(i \alpha/2)} = \cosh{(\alpha/2)} \) sowie \( - i \sin{(i \alpha/2)} = \sinh{(\alpha/2)} \) verwendet (kann man mit den entsprechenden Reihenentwicklungen nachrechnen). Hier zeigt sich ein generelles Phänomen: Boosts und Drehungen hängen über analytische Fortsetzung in den Parametern miteinander zusammen! Das werden wir später noch ausnutzen, wenn wir nach den endlich-dimensionalen Darstellungsmatrizen \(D(g)\) der Gruppe \(SL(2,\mathbb{C})\) fragen.
Nun müssen wir noch nachweisen, dass die über \[ e^{\frac{1}{2} \sigma(\boldsymbol{\alpha})} \, \sigma(x) \, e^{\frac{1}{2} \sigma(\boldsymbol{\alpha})} =: \sigma(\Lambda_b x) \] definierte Matrix \(\Lambda_b\) die Gestalt einer Boostmatrix hat, so wie wir sie am Anfang des Kapitels angegeben haben. Die Rechnung ist etwas länglich und soll hier übersprungen werden (man findet sie z.B. in Kapitel 6 im Skript zur Vorlesung Quantentheorie II von Prof. Schütte im SS 1992 (ITKP, Uni Bonn), Schwerpunkt: die Poincaré-Gruppe, Poincaréskript (.ps, 807kb) ). Tatsächlich ergibt sich für \(\Lambda_b\) genau die gewünschte Gestalt mit \(\boldsymbol{\alpha}\) als Rapiditätsvektor.
Halten wir fest:
|
Zerlegung von Lorentztransformationen in Boosts und Drehungen: Man kann jede Lorentztransformation \(\Lambda\) eindeutig als Produkt einer Drehung \(\Lambda_u\) und eines Boosts \(\Lambda_u\) schreiben: \[ \Lambda = \Lambda_u \Lambda_b \] oder alternativ auch anders herum: \( \Lambda = \Lambda_b' \Lambda_u' \) (mit anderen Dreh- und Boostmatrizen). Für die zugehörigen Matrizen der Überlagerungsgruppe \(SL(2,\mathbb{C})\) gilt: \[ g = u \, e^h \] mit \(u^+ u = 1 \) und \( h^+ = h \) sowie \( \mathrm{Spur} \, h = 0 \). Es gelten die Formeln \[ g \, \sigma(x) \, g^+ = \sigma(\Lambda x) \] \[ u \, \sigma(x) \, u^+ = \sigma(\Lambda_u x) \] \[ e^h \, \sigma(x) \, e^h = \sigma(\Lambda_b x) \] Die \(SU(2)\)-Matrix \(u\) repräsentiert also die Drehungen, während \(e^h\) die Boosts darstellt: \[ u = e^{-\frac{i}{2} \, \sigma(\boldsymbol{w})} = \] \[ = 1 \, \cos{\frac{\omega}{2}} - i \, \sigma(\boldsymbol{e}) \, \sin{\frac{\omega}{2}} \] und \[ e^h = e^{\frac{1}{2} \sigma(\boldsymbol{\alpha})} = \] \[ = 1 \, \cosh{\frac{\alpha}{2}} + \sigma(\boldsymbol{e}) \, \sinh{\frac{\alpha}{2}} \] |
Man sieht hier noch einmal explizit, dass die Überlagerungsgruppe \(SL(2,\mathbb{C})\) nicht unitär ist, denn die Boostmatrizen \(e^h\) sind nicht unitär. Da \(SL(2,\mathbb{C})\) eine Darstellung seiner selbst ist, gibt es demnach (mindestens eine) nicht-unitäre Darstellung. Das unterscheidet \(SL(2,\mathbb{C})\) von kompakten Gruppen wie \(SU(2)\). Für diese galt ja (siehe Kapitel 4.8):
\(SL(2,\mathbb{C})\) ist aufgrund der Boosts aber nicht kompakt, denn die Rapidität \(\boldsymbol{\alpha}\) kann beliebig große Werte in \(\mathbb{R}^3\) annehmen und liefert für jeden Wert eine andere Boostmatrix. Daher läuft die Suche nach unitären Darstellungen auch anders ab als bei der Drehgruppe bzw. bei \(SU(2)\). Insbesondere sind die unitären Darstellungen bei nicht-kompakten Gruppen unendlich-dimensional – wir kommen etwas weiter unten darauf zurück.
Die \(SL(2,\mathbb{C})\)-Boostmatrix \[ e^h = e^{\frac{1}{2} \sigma(\boldsymbol{\alpha})} = \] \[ = 1 \, \cosh{\frac{\alpha}{2}} + \sigma(\boldsymbol{e}) \, \sinh{\frac{\alpha}{2}} \] nimmt für jedes \(\boldsymbol{\alpha}\) einen anderen Wert an (denn \(\sinh{\frac{\alpha}{2}}\) nimmt für jedes \(\alpha\) einen anderen Wert an, siehe Kapitel 3.3). Genauso ist es mit der Lorentz-Boostmatrix \(\Lambda_b\) (aus demselben Grund). Bei den Boostmatrizen gibt es also eine eins-zu-eins-Zuordnung zwischen \(\boldsymbol{\alpha}\) und den Matrizen \( e^h = e^{\frac{1}{2} \sigma(\boldsymbol{\alpha})} \) sowie \( \Lambda_b \). Die Überlagerungsproblematik wie bei den Drehungen tritt bei den Boosts also nicht auf. Das sieht man auch daran, dass \( -e^h \) keine Boostmatrix ist (dagegen ist \( -u \) auch eine Drehmatrix aus \(SU(2)\) ). Die Überlagerungsproblematik hat aber ihren Ursprung gerade darin, dass \(g\) und \(-g\) dieselbe Lorentzmatrix \(\Lambda\) ergeben.
Als Mannigfaltigkeit entsprechen Boosts also dem dreidimensionalen reellen Raum \(\mathbb{R}^3\), unabhängig davon, ob wir Lorentz-Boostmatrizen oder \(SL(2,\mathbb{C})\)-Boostmatrizen betrachten. Die Drehungen entsprechen dagegen der 3-Sphäre \(\mathbb{S}^3\), wenn wir die Überlagerungsgruppe betrachten, bzw. einer 3D-Vollkugel mit Identifikation von bestimmten Oberflächenpunkten, wenn wir die Drehgruppe selbst betrachten (siehe Kapitel 4.8 ).
Da wir nun jede Lorentzmatrix eindeutig als Produkt einer Drehung und eines Boosts schreiben können, ist die Mannigfaltigkeit der Lorentzgruppe (bzw. \(SL(2,\mathbb{C})\)) einfach die Menge aller Punktepaare \( (\boldsymbol{w}, \boldsymbol{\alpha}) \) mit \( \boldsymbol{\alpha}\) aus \(\mathbb{R}^3\) und \(\boldsymbol{w}\) aus dem Parameterraum von \(\mathbb{S}^3\) (bei der Überlagerungsgruppe) oder aus der 3D-Vollkugel (bei der Gruppe selbst, \(\boldsymbol{w}\) ist ja der Drehvektor). Man sagt auch, die Mannigfaltigkeit der Lorentzgruppe ist das Produkt von \(\mathbb{R}^3\) und der Mannigfaltigkeit der Drehgruppe.
Nun ist \(\mathbb{R}^3\) einfach zusammenhängend, macht also keine Probleme beim Zusammenziehen geschlossener Kurven. Die Mannigfaltigkeit der Drehgruppe ist dagegen nicht einfach zusammenhängend, die Mannigfaltigkeit ihrer Überlagerungsgruppe \(SU(2)\) dagegen schon (siehe Kapitel 4.8). Es sind also die Drehungen, die den Übergang zur einfach zusammenhängenden Überlagerungsgruppe \(SL(2,\mathbb{C})\) erzwingen, wenn man alle projektiven unitären Darstellungen der Lorentzgruppe in der Quantentheorie erfassen möchte.
Wenn wir analog zur Behandlung der Drehgruppe in Kapitel 4.8 vorgehen wollten, so müssten wir jetzt die Lie-Algebra der Lorentzgruppe untersuchen, eine hermitesche Darstellung der Lie-Algebra konstruieren, über die Exponentialfunktion dann unitäre Darstellungen der Lorentzgruppe gewinnen und dann die Wirkung dieser Darstellungen zusammen mit Raum-Zeit-Translationen betrachten. Das führt jedoch zu Problemen, denn es gibt keine endlich-dimensionalen unitären Darstellungen der Poincarégruppe, denn diese ist nicht kompakt. So werden die Boost-Generatoren im endlich-dimensionalen Fall typischerweise durch anti-hermitesche Matrizen dargestellt, so dass daraus über die Exponentialabbildung keine unitären Matrizen entstehen.
Es ist daher sinnvoll, bei der Suche nach unitären Darstellungen hier anders vorzugehen: Man bezieht Raum-Zeit-Translationen von Anfang an mit ein, so dass man Eigenvektoren zu Energie und Impuls zur Verfügung hat. Die Wirkung von bestimmten Boosts kann man dann sehr einfach auf diesen Vektoren angeben, was automatisch zu unendlich-dimensionalen Darstellungen führt (nur diese können hier unitär sein). Beispielsweise betrachtet man bei Masse größer Null Boosts in das Ruhesystem und aus dem Ruhesystem heraus. In dem Ruhesystem selbst braucht man dann nur noch Drehungen zu betrachten, und deren Darstellung kennt man. Wir sind in Kapitel 3.5 bereits darauf eingegangen. Ich möchte in diesem Kapitel aber versuchen, die Bezeichnungen etwas zu vereinfachen.
Die folgende Darstellungsweise orientiert sich an Steven Weinberg: The Quantum Theory of Fields, Vol. 1, Kapitel 2.5 (Seite 63). Man findet ähnliche Darstellungen in vielen Texten zur Poincarégruppe.
In Kapitel 4.7 haben wir die Eigenvektoren \( |E, \boldsymbol{p}\rangle \) von \(\hat{H}\) und \(\hat{\boldsymbol{P}}\) kennengelernt. Wir fassen nun \(\hat{H}\) und \(\hat{\boldsymbol{P}}\) zu einem Vierervektor-Operator \[ \hat{P} := (\hat{P}^\mu) = (\hat{H}, \hat{\boldsymbol{P}}) \] zusammen (ob der Begriff Vierervektor gerechtfertigt ist, werden wir noch sehen). Analog schreiben wir den Eigenvektor \( |E, \boldsymbol{p}\rangle \) als \( |p, \sigma \rangle \) mit
| \[ \hat{P}^\mu \, |p, \sigma\rangle = p^\mu \, |p, \sigma\rangle \] |
Der Zusatzindex \(\sigma\) soll andeuten, dass es mehrere Vektoren geben kann, die diese Gleichung erfüllen (nicht mit den Paulimatrizen verwechseln!). Das kennen wir bereits von den Drehungen in Kapitel 4.8 im Zusammenhang mit dem Spin. Analog ist es auch hier. Eine kurze Wiederholung:
Der Sammelindex \(\sigma\) berücksichtigt die Möglichkeit, dass es neben dem Impuls weitere Freiheitsgrade des Systems gibt, die sich bei einer Poincarétransformation verändern. Allgemein könnte \(\sigma\) sogar kontinuierlich sein (beispielsweise wenn \(\sigma\) den Relativimpuls zweier freier Teilchen darstellt – dann wäre \(p\) der Gesamt-Viererimpuls der beiden Teilchen).
Wir wollen nun an dieser Stelle davon ausgehen, dass für einen Einteilchen-Zustand ein diskretes \(\sigma\) ausreicht (das definiert den Begriff Einteilchen-Zustand letztlich). Achtung: Wir haben nicht von einem Elementarteilchen gesprochen! Auch ein gebundenes System wie ein Wasserstoffatom kann als ein Teilchen angesehen werden. Siehe dazu auch Steven Weinberg: The Quantum Theory of Fields Vol. 1, Kapitel 2.5 .
Alle Zustände, die sich durch Poincaré-Transformationsoperatoren ineinander überführen lassen, stellen geboostete oder gedrehte Zustände desselben Teilchens dar. Zustände, die sich so nicht erreichen lassen, gehören zu einem anderen Teilchen bzw. Teilchentyp. Die Zustände zu einem Teilchen bilden also bei Poincaré-Transformationen einen irreduziblen Raum, d.h. sie lassen sich durch geeignete Poincaré-Transformationen ineinander umrechnen.
Eine Raum-Zeit-Translation \[ h(a) \, x = x + a \] (der Buchstabe \(g\) ist schon für die \(SL(2,\mathbb{C})\)-Matrizen vergeben) um die Zeit \(\tau = a^0\) und den räumlichen Vektor \(\boldsymbol{a}\) entspricht nun dem Operator \[ T_{h(a^0)} \, T_{h(\boldsymbol{a})} = \] \[ = e^{i a^0 \hat{H}} \, e^{- i \boldsymbol{a \hat{P}}} = \] \[ = e^{i \, (a^0 \hat{H} - \boldsymbol{a \hat{P}})} = \] \[ = e^{i g(a,\hat{P})} = \] \[ = e^{i a^\mu \hat{P}_\mu} = \] \[ = e^{i a \hat{P}} =: T_{h(a)} \] Dabei steht \( g(a,\hat{P}) = a \hat{P} = a^0 \hat{H} - \boldsymbol{a \hat{P}}\) mit \( \hat{H} = \hat{P}^0 \) für die Minkowski-Metrik. Nun sieht man auch, warum wir in Kapitel 4.7 die Vorzeichen gerade so gewählt haben: Man kann jetzt Raum- und Zeittranslationen sehr schön zu einer einzigen Raum-Zeit-Translation zusammenfassen (\(\hat{H}\) und \(\hat{\boldsymbol{P}}\) vertauschen ja).
In Kapitel 4.8 hatten wir uns angesehen, wie sich eine Drehung auf einen Eigenzustand zum Impulsoperator auswirkt. Analog schauen wir uns jetzt an, wie sich eine Lorentztransformation \(\Lambda\) auf einen solchen Zustand auswirkt. Auf diese Weise können wir verifizieren, dass der Operator \( \hat{P}^\mu \) sich wie ein Vierervektor verhält. Für den Operator der Lorentztransformation schreiben wir \(T_g\), analog zum Drehoperator \(T_u\). Dabei steht \(g\) für eine \(SL(2,\mathbb{C})\)-Matrix, die zu \(\Lambda\) gehört.
Gehen wir analog zu Kapitel 4.8 vor und schauen uns dazu an, ob Lorentz-Transformationen und Raum-Zeit-Translationen vertauschen: \[ \Lambda \, h(a) \, x = \] \[ = \Lambda \, (x + a) = \] \[ = \Lambda \, x + \Lambda \, a = \] \[ = h(\Lambda a) \, \Lambda \, x \] Translationen und Lorentz-Transformationen vertauschen also nicht miteinander. Die obige Gleichung können wir eins-zu-eins auf die quantenmechanischen Operatoren übertragen. Das geht, da es hier keine Zentralladungen gibt (anders als bei der Galileigruppe). Phasen können nur über die Überlagerungsgruppe auftreten. Das berücksichtigen wir, indem wir \(\Lambda\) durch \(T_g\) ersetzen, wobei \(g\) aus der Überlagerungsgruppe \(SL(2,\mathbb{C})\) ist: \[ T_g \, e^{i \, g(a,\hat{P})} = e^{i \, g(\Lambda a, \hat{P})} \, T_g \] (das \(g\) im Exponenten bezeichnet die Lorentz-Metrik, das tiefgestellte \(g\) bezeichnet die \(SL(2,\mathbb{C})\)-Matrix). Auf der rechten Seite können wir nun \( g(\Lambda a, \hat{P}) = g(a, \Lambda^{-1} \hat{P}) \) verwenden: \[ T_g \, e^{i \, g(a,\hat{P})} = e^{i \, g(a, \Lambda^{-1} \hat{P})} \, T_g \] Abgeleitet nach den einzelnen \(a_\mu\) bei \(a=0\) ergibt \[ T_g \, \hat{P} = (\Lambda^{-1} \hat{P}) \, T_g \] und multipliziert mit \(\Lambda\) dann \[ T_g \, (\Lambda \hat{P}) = \hat{P} \, T_g \] Damit können wir nun angeben, wie sich eine Lorentztransformation auf einen Eigenvektor \( |p,\sigma\rangle \) des Vierer-Impulsoperators auswirkt: \[ \hat{P} \, T_g \, |p,\sigma\rangle = \] \[ = T_g \, (\Lambda \hat{P}) \, |p,\sigma\rangle = \] \[ = T_g \, (\Lambda p) \, |p,\sigma\rangle = \] \[ = (\Lambda p) \, T_g \, |p,\sigma\rangle \] d.h. der Lorentz-transformierte Zustand \(T_g \, |p,\sigma\rangle \) ist ein Eigenzustand zum Vierer-Impulsoperator \(\hat{P}\) zum Eigenwert \( \Lambda p\). Der Vierer-Impuls des Zustandes wurde also genau so transformiert, wie wir das für einen Vierervektor erwarten – eine nachträgliche Rechtfertigung für unsere Notation!
Man könnte nun versucht sein, deshalb \( T_g \, |p,\sigma\rangle = |\Lambda p,\sigma\rangle \) zu schreiben. Doch Vorsicht: Der Index \(\sigma\) deutet ja bereits an, dass es mehrere Zustände zu einem Viererimpuls geben kann. Wir wissen nur, dass \(T_g \, |p,\sigma\rangle \) eine Linearkombination der \( |\Lambda p,\sigma\rangle \) sein muss: \[ T_g \, |p,\sigma\rangle = \] \[ = \sum_{\sigma'} \, |\Lambda p,\sigma' \rangle \, C_{\sigma'\sigma}(g,p) \] mit entsprechenden Entwicklungskoeffizienten \( C_{\sigma'\sigma}(g,p) \), die von \(g\) und \(p\) abhängen können. Versuchen wir, mehr über diese Koeffizienten herauszufinden. Dazu ist es nützlich, die Vierervektoren \(p\) in Klassen zu unterteilen, so dass sich die \(p\) in einer Klasse alle per Lorentztransformation ineinander umwandeln lassen. Anschaulich kann man sich vorstellen, dass man ein Teilchen allen möglichen Boosts und Drehungen unterwirft und so alle möglichen Viererimpulse erzeugt, die das Teilchen aufweisen kann. Die verschiedenen Impulsklassen entsprechen dann verschiedenen Teilchen, denn ihre Impulse lassen sich nicht durch Boosts und Drehungen ineinander umwandeln.
In jeder Impulsklasse kann man nun einen Viererimpuls-Repräsentanten \(k\) auswählen, eine Art Standard-Viererimpuls, der die Klasse repräsentiert. Für jeden anderen Viererimpuls \(p\) aus dieser Klasse gibt es dann mindestens eine Lorentztransformation \(\Lambda_p\), so dass \[ p = \Lambda_p \, k \] ist (natürlich hängt \(\Lambda_p\) auch noch von \(k\) ab, aber da wir \(k\) pro Klasse fest vorgeben werden, wollen wir diese Abhängigkeit in der Schreibweise hier unterdrücken, sonst wird es unleserlich).
Welche Viererimpulsklassen und damit welche \(k\) gibt es überhaupt?
Nun, zunächst einmal lässt \(\Lambda_p\) die Minkowskimetrik von \(p\)
invariant, d.h. jeder Wert von \(g(p,p) =: p^2\) liefert eine eignene Impulsklasse.
Da wir außerdem nur die Zusammenhangskomponente mit der Eins betrachten
(also die Lorentztransformationen, zu denen es ein \(g \in SL(2,\mathbb{C})\) gibt
– keine Raum-Zeit-Spiegelungen),
ändert sich für \(p^2 \gt 0 \) und
\( p^2 = 0 \) auch das Vorzeichen der Energie \(p^0\) nicht.



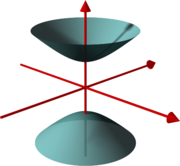
Hier die drei Fälle (im Folgenden ist \(m\) immer eine positive reelle Zahl):
Ein massives Teilchen entspricht der oberen Massenschale im Bild links. Standardvektor ist \[ k = \begin{pmatrix} m \\ \boldsymbol{0} \end{pmatrix} \] Das ist der Viererimpuls im Ruhesystem, denn der räumliche Impuls ist Null und die Energie ist positiv und gleich der Masse (in natürlichen Einheiten).
Ein masseloses Teilchen entspricht dem oberen Lichtkegel im mittleren Bild (so dass die Energie positiv ist). Standardvektor ist \[ k = \begin{pmatrix} \kappa \\ \kappa \, \boldsymbol{e}_3 \end{pmatrix} \] Ein Ruhesystem gibt es hier nicht.
Die unteren Massenschalen entsprechen negativen Energien. Für Einteilchenzustände sehen wir diese negativen Energien als unphysikalisch an. Wenn nämlich Teilchen negative Energien besitzen könnten und andere Teilchen positive Energien, so könnte beispielsweise aus dem Nichts heraus ein Teilchen mit positiver Energie und ein Teilchen mit gleich großer negativer Energie und entgegengesetztem räumlichen Impuls entstehen, ohne dass die Energie-Impuls-Erhaltung verletzt wäre. In diesem Sinne wäre das Vakuum instabil, denn es könnte ständig solche Teilchenpaare erzeugen. Daher betrachten wir negative Teilchenenergien hier nicht weiter. Beim Aufbau einer Quantenfeldtheorie mit Wechselwirkung werden sie aber später wieder ins Spiel kommen und müssen geeignet in den Formalismus eingebracht werden – das Ergebnis sind die Antiteilchen. Dabei muss man dafür sorgen, dass kein Teilchen- oder Antiteilchen-Zustand eine niedrigere Energie als das Vakuum hat, was letztlich auch eine Bedingung für den Vakuumzustand ist. Eine zweite Bedingung an den Vakuumzustand \( |0\rangle \) ist, dass für ihn \[ \hat{P}^\mu |0\rangle = 0 \] gilt. Das hat zur Folge, dass Poincarétransformationen den Vakuumzustand nicht ändern, d.h. die Poincarégruppe wird auf diesem Zustand trivial dargestellt.
Der Fall 3 mit negativem \( p^2 \) entspäche bei Anwendung der Formel \( p = m u \) einer Überlicht-Vierergeschwindigkeit \(u\). Man spricht hier von sogenannten Tachyonen. Überlichtgeschwindigkeit führt aber zu Kausalitätsproblemen und muss daher hier ebenfalls als unphysikalisch angesehen werden. Aber auch ohne die Formel \( p = m u \) wäre ein negatives \(p^2\) unphysikalisch: Durch einen Boost könnte eine positive Teilchenenergie \(p^0\) in eine negative Teilchenenergie oder auch auf Null verändert werden – wieder mit dem Ergebnis, dass beliebig viele Teilchenpaare aus dem Vakuum entstehen könnten, ohne die Energie-Impuls-Erhaltung zu verletzen. Bei bosonischen Stringtheorien tauchen solche Zustände mit negativem \( p^2 \) tatsächlich auf und signalisieren damit eine Inkonsistenz in der Theorie (man spricht wegen der möglichen Teilchenpaarerzeugung aus dem Nichts heraus von einem instabilen Vakuum). Erst die Einführung von Fermionen über die Supersymmetrie behebt dieses Problem in der Stringtheorie (siehe Kapitel 6.2).
Zurück zu unseren Impuls-Zuständen. Die Zustände für die Standardvektoren \(k\) lauten \[ |k,\sigma\rangle \] Da \( p = \Lambda_p \, k \) ist, führt die Anwendung von \(T_{g(p)}\) auf \( |k,\sigma\rangle \) zu einem Zustand mit Impuls \(p\) (dabei ist \(g(p)\) eine \(SL(2,\mathbb{C})\)-Matrix zu \(\Lambda_p\)). Um die \(\sigma\)-Indices für verschiedene Impulse in Beziehung zueinander zu setzen, können wir festlegen: \[ |p,\sigma\rangle := N_p \, T_{g(p)} \, |k,\sigma\rangle \] mit einer \(p\)-abhängigen reellen Normierung \( N_p \), die wir später passend wählen werden. Wenden wir nun irgendeine Lorentztransformation \( T_g \) mit zugehörigem \(\Lambda\) auf diese Gleichung an, fügen rechts die Identität \( T_{g(\Lambda p)} \, T_{g(\Lambda p)^{-1}} \) ein und nutzen die Gruppen-Darstellungseigenschaft von \(T\), so erhalten wir. \[ T_g \, |p,\sigma\rangle = \] \[ = N_p \, T_g \, T_{g(p)} \, |k,\sigma\rangle = \] \[ = N_p \, T_{g(\Lambda p)} \, T_{g(\Lambda p)^{-1}} \, T_g \, T_{g(p)} \, |k,\sigma\rangle = \] \[ = N_p \, T_{g(\Lambda p)} \, T_{g(\Lambda p)^{-1} \, g \, g(p)} \, |k,\sigma\rangle = \, (*) \] Die \(SL(2,\mathbb{C})\)-Matrix \( g(\Lambda p)^{-1} \, g \, g(p) \) entspricht einer Lorentztransformation, die die Impulse folgendermaßen umwandelt: \[ k \rightarrow p \rightarrow \Lambda p \rightarrow k \] Das war der Sinn der Umformung oben. Diese Lorentztransformation ändert den Standardvektor \(k\) nicht! Man nennt die Gruppe dieser Lorentztransformationen zu festem \(k\) die kleine Gruppe (little group) oder auch Stabilitätsgruppe. Mathematiker sprechen auch von der isotropy subgroup (siehe z.B. John Baez: Unitary representations of the Poincaré group). Die entsprechenden \(SL(2,\mathbb{C})\)-Matrizen wollen wir mit \(u\) bezeichnen (da sie z.B. für Teilchen mit Masse unitär sind, wie wir noch sehen werden; bitte nicht mit der Vierergeschwindigkeit verwechseln):
|
Die kleine Gruppe (little group): Die \(SL(2,\mathbb{C})\)-Matrizen \[ u := g(\Lambda p)^{-1} \, g \, g(p) \] zu festem Standard-Viererimpulsvektor \(k\) bilden die sogenannte kleine Gruppe zu \(k\). Die zugehörige Lorentzmatrix \(\Lambda_u\) verändert \(k\) nicht: \[ \Lambda_u \, k = k \] Man bezeichnet \(u\) bzw. \(\Lambda_u\) auch als Wigner-Rotation. Dabei hängt \(u\) natürlich von \(p\) und \(k\) ab, denn \(p\) und \(k\) gehen in die Definition von \(g(p)\) und \(g(\Lambda p)\) ein: \( p = \Lambda_p \, k \) und \(g(p)\) ist die \(SL(2,\mathbb{C})\)-Matrix zu \(\Lambda_p\). Zur Schreibweise: \(u\) kann, muss aber nicht zwingend unitär sein – das hängt von \(k\) ab – schauen wir uns noch an. |
Die Gleichung \( u = g(\Lambda p)^{-1} \, g \, g(p) \) kann man übrigens zu \[ g = g(\Lambda p) \, u \, g(p)^{-1} \] umformen, was sich sehr schön interpretieren lässt: Erst wandelt man \(p\) mit \(g(p)^{-1}\) zum Standardvektor \(k\) um (man geht bei massiven Teilchen beispielsweise ins Ruhesystem), dann dreht man sich mit \(u\) um \(k\) herum in eine passende Richtung (ohne \(k\) zu ändern), so dass man schließlich mit \(g(\Lambda p)\) zum Zielvektor \(\Lambda p\) gelangt.
Wozu brauchen wir die kleine Gruppe? Da sie \(k\) nicht ändert, kann sie sich bei \( |k,\sigma\rangle \) nur noch auf die \(\sigma\)-Indices auswirken, so wie sich der Spin-Drehungsoperator \( e^{- i \boldsymbol{w \hat{S}}} \) in Kapitel 4.8 nur auf die Spin-Indices ausgewirkt hat. Da wir in Kapitel 4.8 nur Drehungen und keine Boosts hatten, mussten wir dies dort für den Spinoperator explizit fordern. Bei der kleinen Gruppe dagegen bewirkt die Konstruktion dieser Gruppe automatisch, dass der Standardimpuls nicht geändert wird. Wir haben also
| \[ T_u \, |k,\sigma\rangle = \] \[ = \sum_{\sigma'} \, |k,\sigma'\rangle \, D_{\sigma' \sigma}(u) \] |
mit einer entsprechenden Darstellungsmatrix \( D_{\sigma' \sigma}(u) \) der kleinen Gruppe (so wie die Drehmatrizen eine Matrixdarstellung von \(SU(2)\) liefern). Man beachte: nur für unitäres \(u\) ist \( D_{\sigma' \sigma}(u) \) (ggf. nach Ausreduktion und Basiswahl) eine Drehmatrix – wir kommen noch darauf zurück.
Damit können wir nun oben bei (*) weiterrechnen: \[ T_g \, |p,\sigma\rangle = \] \[ = N_p \, T_{g(\Lambda p)} \, T_{g(\Lambda p)^{-1} \, g \, g(p)} \, |k,\sigma\rangle = \] \[ = N_p \, T_{g(\Lambda p)} \, T_u \, |k,\sigma\rangle = \] \[ = N_p \, T_{g(\Lambda p)} \, \sum_{\sigma'} \, |k,\sigma'\rangle \, D_{\sigma' \sigma}(u) \] Hier können wir nun die Definition \[ |p,\sigma\rangle := N_p \, T_{g(p)} \, |k,\sigma\rangle \] von oben verwenden, darin \(p\) durch \(\Lambda p\) und \(\sigma\) durch \(\sigma'\) ersetzen \[ |\Lambda p,\sigma'\rangle = N_{\Lambda p} \, T_{g(\Lambda p)} \, |k,\sigma'\rangle \] und dies oben rechts verwenden:
| \[ T_g \, |p,\sigma\rangle = \] \[ = \frac{N_p}{N_{\Lambda p}} \, \sum_{\sigma'} \, |\Lambda p,\sigma'\rangle \, D_{\sigma' \sigma}(u) \] |
Damit haben wir die Entwicklungskoeffizienten \( C_{\sigma' \sigma}(g,p) \) in \[ T_g \, |p,\sigma\rangle = \] \[ = \sum_{\sigma'} \, |\Lambda p,\sigma' \rangle \, C_{\sigma' \sigma}(g,p) \] (bis auf die Normierung) eindeutig bestimmt. Es genügt dafür, die Darstellungen der kleinen Gruppe zu kennen. Man spricht daher auch von einer induzierten Darstellung, denn die Darstellungen der kleinen Gruppe induzieren Darstellungen für die gesamte Poincarégruppe. Vorsicht: Die kleine Gruppe ist als Untergruppe von \(SL(2,\mathbb{C})\) zu sehen, denn insgesamt wollen wir ja eine Darstellung \(T_g\) von \(SL(2,\mathbb{C})\) haben. Daher sind nicht alle Darstellungen der jeweiligen kleinen Gruppe zulässig (wird bei masselosen Teilchen wichtig, siehe unten).
Nun zur Normierung: Unser Ziel ist es ja, eine unitäre Darstellung der Überlagerungsgruppe zu erreichen (projektive Phasen hatten wir oben bereits ausgeschlossen, da die Lie-Algebra keine Zentralladungen zulässt). Also müssen wir uns über das Skalarprodukt und die Normierung der Zustände Gedanken machen.
Die Zustände \( |p,\sigma\rangle \) wollen wir als Einteilchenzustände interpretieren, was insbesondere bedeuten soll, dass \(\sigma\) nur endlich viele diskrete Werte annehmen kann. Nun kommutiert der Hamiltonoperator \( \hat{H} = \hat{P}^0 \) als Darstellungsoperator des Zeittranslations-Generators mit \(\hat{\boldsymbol{P}}\) (und natürlich mit sich selbst). Daher ändert sich der Viererimpuls \( p = (E, \boldsymbol{p}) \) des Zustandes \( |p,\sigma\rangle \) zeitlich nicht, wie wir am Ende von Kapitel 4.7 gesehen haben. Man spricht entsprechend von einem freien Teilchen. Äußere Einflüsse, die Energie und Impuls des Teilchens ändern könnten, sind ausgeschlossen. Diese Einflüsse (z.B. äußere Felder) würden ja auch die Raum-Zeit-Symmetrie zerstören, von der wir in diesem Kapitel ausgehen.
Übrigens: Nur bei einem freien Teilchen ist es überhaupt möglich, Energie und Impuls genau zu messen, denn dafür benötigt man eine bestimmte Messzeit, in der sich beides nicht ändert. Diese Messzeit ist umso länger, je genauer man Energie und Impuls bestimmen möchte. Man kann auch sagen: Nur bei einem freien Teilchenzustand sind Energie und Impuls definierte und beliebig genau messbare Größen. Mehr dazu siehe Landau, Lifschitz: Lehrbuch der theoretischen Physik, Band IV (Quantenelektrodynamik), Akademie-Verlag Berlin 1986. Besonders interessant ist Hendrik van Hees: Unschärferelation und relativistische Quantentheorie, speziell das Kapitel über Impulsmessung.
Wir wissen aus Kapitel 4.5: Das Skalarprodukt liefert die Wahrscheinlichkeitsamplitude für ein Messergebnis, und der quadrierte Betrag der Wahrscheinlichkeitsamplitude liefert die entsprechende Wahrscheinlichkeit. Wenn wir also zur Zeit \(t\) einen Einteilchenzustand \( |p,\sigma\rangle \) haben, so werden wir zu dieser Zeit den Viererimpuls \(p\) und den Messwert \(\sigma\) mit der Wahrscheinlichkeit 1 messen, andere Impulse oder Werte von \(\sigma\) dagegen überhaupt nicht. Für die Wahrscheinlichkeitsamplitude und das entsprechende Skalarprodukt würden wir daher erwarten: \[ \langle p',\sigma' | p, \sigma \rangle = \delta_{p,p'} \, \delta_{\sigma, \sigma'} \] Das wäre auch korrekt, wenn der Viererimpuls nur diskrete Werte annehmen könnte. Da der Impuls aber kontinuierliche Werte annehmen kann, ist die Wahrscheinlichkeit, einen ganz bestimmten Impuls zu messen, gleich Null, denn man wird immer eine (wenn auch beliebig kleine) Abweichung haben. Bei kontinuierlichen Größen muss man nach der Wahrscheinlichkeit dafür fragen, dass diese Größe in einem bestimmten Bereich liegt, den man dann beliebig klein (aber endlich) wählen kann. Um diesen Fall zu erfassen, müssen wir unseren quantenmechanischen Formalismus etwas erweitern.
In Kapitel 4.5 haben wir die Zerlegung \[ |\psi\rangle = \sum_n \, a_n \, |n\rangle \] kennengelernt mit den Normierungen \[ \langle n | n' \rangle = \delta_{n,n'} \] sowie \[ \sum_n \, |a_n|^2 = 1 \] Dabei ist \[ a_n = \langle n | \psi \rangle \] die Wahrscheinlichkeitsamplitude dafür, bei dem Zustand \( | \psi \rangle \) die Messwerte zu finden, die den Zustand \( | n \rangle \) kennzeichnen. Dabei steht \(n\) für einen Satz diskreter Messwerte und die Summe geht über alle diese diskreten Messwertsätze. Diesen Formalismus müssen wir nun auf kontinuierliche Messwerte übertragen. Wie das geht, kennen wir aus Kapitel 4.7, wo wir das für die kontinuierlichen Impulse bereits getan haben: \[ | \psi \rangle = \int d^3p \, f(\boldsymbol{p}) \, | \boldsymbol{p} \rangle \] Aus der Summe wird also ein Integral, und aus der Amplitude \( a_n \) wird die Amplitudendichte \( f(\boldsymbol{p}) \). Entsprechend ist \( \int_G d^3p \, |f(\boldsymbol{p})|^2 \) die Wahrscheinlichkeit dafür, den Impuls im Gebiet (Wertebereich) \(G\) zu finden, wobei man \(G\) beliebig klein (aber endlich) machen kann. Die Normierung lautet dann \[ \int d^3p \, |f(\boldsymbol{p})|^2 = 1 \] wenn man über alle Impulse integriert, denn irgendeinen Impuls wird man messen. Um analog zu \( a_n = \langle n | \psi \rangle \) nun \[ f(\boldsymbol{p}) = \langle \boldsymbol{p} | \psi \rangle \] mit einer entsprechenden Linearform \( \langle \boldsymbol{p} | \) schreiben zu können, muss gelten: \[ | \psi \rangle = \] \[ = \int d^3p \, f(\boldsymbol{p}) \, | \boldsymbol{p} \rangle = \] \[ = \int d^3p \, \langle \boldsymbol{p} |\psi \rangle \, | \boldsymbol{p} \rangle = \] \[ = \int d^3p \, | \boldsymbol{p} \rangle \, \langle \boldsymbol{p} | \psi \rangle \] d.h. analog zur Formel \( 1 = \sum_n \, | n \rangle \, \langle n | \) aus Kapitel 4.5 haben wir hier die Formel \[ 1 = \int d^3p \, | \boldsymbol{p} \rangle \, \langle \boldsymbol{p} | \] Diese Formel führt zu der folgenden Normierung für \( \langle \boldsymbol{p}' | \boldsymbol{p} \rangle \): \[ f(\boldsymbol{p}') = \langle \boldsymbol{p}' | \psi \rangle = \] \[ = \langle \boldsymbol{p}'| \, \int d^3p \, f(\boldsymbol{p}) \, | \boldsymbol{p} \rangle = \] \[ = \int d^3p \, f(\boldsymbol{p}) \, \langle \boldsymbol{p}' | \boldsymbol{p} \rangle = \] \[ = \int d^3p \, f(\boldsymbol{p}) \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \] denn nur so ergibt das Integral rechts wieder \( f(\boldsymbol{p}') \). Es muss also \[ \langle \boldsymbol{p}' | \boldsymbol{p} \rangle = \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \] gelten, analog zur Normierung \( \langle n | n' \rangle = \delta_{n,n'} \) im diskreten Fall. Dabei ist \( \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \) die bekannte Delta-Funktion (besser wäre Delta-Funktional oder Delta-Distribution). Man kann sich die Delta-Funktion als sehr spitze Funktion vorstellen, die aus dem Integral gleichsam nur die Werte eines unendlich dünnen Bereichs herausfischt. Details zur Delta-Funktion findet man in Die Grenzen der Berechenbarkeit, Kapitel 5.4.4 sowie unter Wikipedia: Delta-Distribution (hier findet man auch eine anschauliche Erläuterung).
Es wird sich etwas später als nützlich erweisen, einen Faktor \( \frac{1}{a(\boldsymbol{p})} \) mit einer impulsabhängigen positiven reellen Funktion \(a(\boldsymbol{p})\) im Integrationsmaß \( d^3p \) einzufügen, also \( \frac{d^3p}{a(\boldsymbol{p})} \) im Integral zu verwenden (wobei wir \( f(\boldsymbol{p}) = \langle \boldsymbol{p} | \psi \rangle \) beibehalten). Dabei wird später \(a(\boldsymbol{p})\) die Komponente \(p^0\) sein, so dass das Integrationsmaß invariant unter Poincaré-Transformationen wird. Wenn wir dies in den Formeln oben berücksichtigen, so erhalten wir: \[ | \psi \rangle = \] \[ = \int \frac{d^3p}{a(\boldsymbol{p})} \, f(\boldsymbol{p}) \, | \boldsymbol{p} \rangle = \] \[ = \int \frac{d^3p}{a(\boldsymbol{p})} \, | \boldsymbol{p} \rangle \, \langle\boldsymbol{p}|\psi\rangle = \] so dass \[ 1 = \int \frac{d^3p}{a(\boldsymbol{p})} \, | \boldsymbol{p} \rangle \, \langle \boldsymbol{p} | \] und \[ f(\boldsymbol{p}') = \langle \boldsymbol{p}' | \psi\rangle = \] \[ = \langle \boldsymbol{p}' | \, \int \frac{d^3p}{a(\boldsymbol{p})} \, f(\boldsymbol{p}) \, | \boldsymbol{p} \rangle = \] \[ = \int \frac{d^3p}{a(\boldsymbol{p})} \, f(\boldsymbol{p}) \, \langle \boldsymbol{p}' | \boldsymbol{p} \rangle = \] \[ = \int d^3p \, f(\boldsymbol{p}) \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \] d.h. \[ \langle \boldsymbol{p}' | \boldsymbol{p} \rangle = a(\boldsymbol{p}) \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \] Allerdings ist dann \( |f(\boldsymbol{p})|^2 \) nicht mehr die Wahrscheinlichkeits-Dichte für den Impuls, sondern \( |f(\boldsymbol{p})|^2 / a(\boldsymbol{p}) \) ist diese Dichte, denn es gilt: \[ 1 = \langle \psi | \psi \rangle = \] \[ = \int \frac{d^3p}{a(\boldsymbol{p})} \, \langle \psi | \boldsymbol{p} \rangle \, \langle \boldsymbol{p} | \psi \rangle = \] \[ = \int d^3p \, \frac{|f(\boldsymbol{p})|^2}{a(\boldsymbol{p})} \]
Anmerkung:
Bei einer dreidimensionalen kontinuierlichen Zufallsgröße \(\boldsymbol{x}\) mit Wahrscheinlichkeitsdichte \( \eta(\boldsymbol{x}) \) ist allgemein \[ \int_G d^3x \, \eta(\boldsymbol{x}) \] die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(\boldsymbol{x}\) im Gebiet \(G\) liegt. Genau so ist der Begriff Wahrscheinlichkeitsdichte definiert. Die Formel stellt beispielsweise sicher, dass Wahrscheinlichkeiten additiv sind: Bei zwei nicht-überlappenden Gebieten \(G\) und \(G'\) ist die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(\boldsymbol{x}\) in Gebiet \(G\) oder \(G'\) liegt, gerade gleich der Summe der Wahrscheinlichkeiten für die Gebiete \(G\) und \(G'\): \[ \int_{G + G'} d^3x \, \eta(\boldsymbol{x}) = \] \[ = \int_G d^3x \, \eta(\boldsymbol{x}) + \int_{G'} d^3x \, \eta(\boldsymbol{x}) \] Natürlich muss dann \[ \int d^3x \, \eta(\boldsymbol{x}) = 1 \] sein und \( \eta(\boldsymbol{x}) \gt 0 \) für alle \(\boldsymbol{x}\) gelten, damit für jedes beliebige Gebiet \(G\) die Wahrscheinlichkeit positiv ist. Damit kann man ablesen, dass man oben \( |f(\boldsymbol{p})|^2 / a(\boldsymbol{p}) \) als Wahrscheinlichkeitsdichte für die Zufallsgröße \(\boldsymbol{p}\) interpretieren kann. Wir werden bei der Diskussion der Orts-Wahrscheinlichkeitsdichte unten noch einmal darauf zurückkommen. Mehr zum Begriff der Wahrscheinlichkeitsdichte siehe Wikipedia: Dichtefunktion.
Wir wollen nun einen allgemeinen Einteilchenzustand
\( | \psi \rangle \) durch Überlagerung der
Impuls-Einteilchenzustände \( |p, \sigma \rangle \) konstruieren.
Neben dem kontinuierlichen Vierervektor \(p\) taucht noch die diskrete Größe \(\sigma\) auf.
Diese Größe können wir einfach dadurch berücksichtigen
dass wir nicht nur über \(p\) integrieren,
sondern auch über \(\sigma\) summieren, so wie wir das vorher mit \(n\) gemacht haben.
Bleibt die vierdimensionale Größe \(p\).
Müssen wir womöglich zu vierdimensionalen Integralen übergehen?
Im Normalfall hat man es in der Physik mit Zuständen einer bestimmten Masse zu tun. Es gibt zwar selten auch den Fall, dass man Zustände verschiedener Massen überlagern kann (Stichwort Neutrino-Oszillation, siehe Kapitel 4.5), aber solche Zustände wollen wir hier nicht betrachten. Man kann sie ggf. durch Superposition von Zuständen mit definierter Masse aufbauen. Im Folgenden wollen wir also die Einschränkung machen, dass alle Viererimpulse, die wir überlagern wollen, zur selben Masse gehören: \[ g(p,p) = p^2 = m^2 \] mit einer reellen Masse \(m \ge 0 \). Der Einteilchenzustand \( | \psi \rangle \) hat dann ebenfalls diese Masse, d.h. \[ \hat{P}^2 \, | \psi \rangle = m^2 \, | \psi \rangle \] Außerdem wollen wir nur physikalisch interpretierbare Viererimpulse zulassen, d.h. \(p^2\) und \(p^0\) dürfen nicht negativ sein (siehe oben). So ist sichergestellt, dass bei einer Energie-Impulsmessung am Zustand \( | \psi \rangle \) nur physikalisch interpretierbare Messwerte möglich sind, und dass \[ p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \] ist, so wie das bei einem Teilchen mit Masse \(m\) und Impuls \(\boldsymbol{p}\) sein muss.
Bei fester Masse ist also \(p^0\) keine unabhängige Variable mehr, sondern eine Funktion von \(\boldsymbol{p}\). Wir integrieren also über den dreidimensionalen Vektor \(\boldsymbol{p}\) und nicht über den Vierervektor \(p\). Allerdings wäre es hilfreich, denn wir ein Poincaré-invariantes Integrationsmaß verwenden könnten. In Kapitel 4.8 war es nämlich bei der Betrachtung von Drehungen auch sehr nützlich, dass das Integrationsmaß \(d^3p\) drehinvariant war.
Wie findet man ein solches Integrationsmaß? Starten wir mit dem vierdimensionalen Integrationsmaß \(d^4p = dp^0 \, d^3p \), das wir verwendet hätten, wenn \(p^0\) unabhängig von \(\boldsymbol{p}\) wäre. Dieses Integrationsmaß verändert sich nicht bei Lorentztransformationen: Wenn \[ p' = \Lambda \, p \] ist, so ist \[ d^4p' = |\det{\Lambda}| \, d^4p = d^4p \] denn \[ |\det{\Lambda}| = 1 \] Das folgt aus \[ \Lambda^T \, g \, \Lambda = g \] mit der metrischen Minkowski-Matrix \(g\) (siehe Kapitel 3.1), denn dann ist \[ \det{\Lambda^T} \, \det{g} \, \det{\Lambda} = \det{g} \] und somit \[ (\det{\Lambda})^2 = 1 \] Wir können aber nicht über alle Viererimpulse \(p\) integrieren, denn es soll ja \( p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \) sein. Das erreichen wir, wenn wir in das Integrationsmaß eine Delta-Funktion sowie eine Theta-Funktion einfügen (die Theta-Funktion \(\Theta(x)\) ist eins für \(x \ge \) und Null sonst): \[ d^4p \, \delta(p^2 - m^2) \, \Theta(p^0) \] mit \(p^2 = g(p,p) = (p^0)^2 - \boldsymbol{p}^2\).
Die Integration läuft damit nur noch über die oben dargestellten dreidimensionalen Unterräume im Vierer-Impulsraum, die sich physikalisch interpretieren lassen. Man kann auch sagen: Die Integration läuft über \(\boldsymbol{p}\) mit \( p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \). Dabei ist das Integrationsmaß \( d^4p \, \delta(p^2 - m^2) \, \Theta(p^0) \) Poincaré-invariant (Zeitspiegelungen hatten wir ausgeschlossen und \(m \ge 0\) ist eine reelle Zahl).
Nun ist die Schreibweise mit \( \delta(p^2 - m^2) \, \Theta(p^0) \) noch etwas unhandlich. Es wäre schön, wenn man diese Distributionen explizit auswerten könnte und ein invariantes dreidimensionales Integrationsmaß angeben könnte. Dazu müssen wir die Integration über \(p^0\) ausführen: \[ \int d^4p \, \delta(p^2 - m^2) \, \Theta(p^0) \, F(p) = \] \[ = \int d^3p \, \int dp^0 \, \delta((p^0)^2 - \boldsymbol{p}^2 - m^2) \, \cdot \] \[ \, \cdot \Theta(p^0) \, F(p^0,\boldsymbol{p}) = \] \[ = \int d^3p \, \int \frac{dp^0}{2 \sqrt{m^2 + \boldsymbol{p}^2}} \, \cdot \] \[ \cdot \, \delta \left( p^0 - \sqrt{m^2 + \boldsymbol{p}^2} \right) \, F(p^0,\boldsymbol{p}) = \] \[ = \int \frac{d^3p}{2 p^0} \, F(p^0,\boldsymbol{p}) \] wobei in der letzten Zeile \( p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \) einzusetzen ist. Dabei haben wir die Rechenregeln für die Delta-Funktion angewendet, wie sie beispielsweise in Wikipedia: Delta-Distribution dargestellt sind. Hier eine kurze Motivation der angewendeten Regel in Physiker-Kurzschreibweise für eine Funktion \(g(x)\) mit nur einer einfachen Nullstelle und positiver Ableitung (die Theta-Funktion oben sorgt dafür): \[ \int dx \, \delta(g(x)) \, F(x) = \] \[ = \int \frac{dx}{dg} \, dg \, \delta(g) \, F(x(g)) = \] \[ = \int \frac{1}{dg/dx} \, dg \, \delta(g) \, F(x(g)) = \] \[ = \frac{1}{dg/dx} \bigg|_{x_0} \, F(x_0) \] mit \( g(x_0) = 0 \) oder anders gesagt \( x_0 = x(g)|_{g=0} \) . Statt \(x\) haben wir oben die Variable \(p^0\) und \( g(p^0) = (p^0)^2 - \boldsymbol{p}^2 - m^2 \) und die Theta-Funktion sorgt dafür, dass nur positive \(p^0\) inklusive Null eine Rolle spielen.
Damit haben wir unser dreidimensionales Poincaré-invariantes Integrationsmaß:
|
Poincaré-invariantes Integrationsmaß für die Integration über \(p\): \[ \frac{d^3p}{2p^0} \] mit \[ p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \] (den Faktor \(2\) im Nenner kann man auch weglassen, aber er wird meist so verwendet)
|
Jetzt wird auch klar, warum wir oben das Integrationsmaß \( \frac{d^3p}{a(\boldsymbol{p})} \) betrachtet haben. Wir setzen nun \[ a(\boldsymbol{p}) = 2 p^0 = 2 \sqrt{m^2 + \boldsymbol{p}^2} \] in allen Formeln oben ein, berücksichtigen zusätzlich den diskreten Freiheitsgrad \(\sigma\), schreiben \[ |\boldsymbol{p}, \sigma \rangle \] mit dem räumlichen Impuls \( \boldsymbol{p} \) statt \( |p, \sigma \rangle \) mit dem Viererimpuls \(p\) (denn \(p^0\) ist ja bei fester Masse keine unabhängige Größe mehr) und erhalten:
|
Skalarprodukt, Superposition und Normierung von Impulszuständen mit einem Poincaré-invarianten Integrationsmaß: In allen folgenden Formeln gilt \( p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \) \[ | \psi \rangle = \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, f_\sigma(\boldsymbol{p}) \, | \boldsymbol{p}, \sigma \rangle \] \[ 1 = \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, |\boldsymbol{p}, \sigma \rangle \, \langle \boldsymbol{p}, \sigma | \] \[ f_\sigma(\boldsymbol{p}) = \langle \boldsymbol{p}, \sigma | \psi \rangle \] \[ [f_\sigma(\boldsymbol{p})]^* = \langle \psi | \boldsymbol{p}, \sigma \rangle \] \[ \langle \boldsymbol{p}', \sigma' | \boldsymbol{p}, \sigma \rangle = 2p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \, \delta_{\sigma, \sigma'} \] \[ \langle \psi' | \psi \rangle = \] \[ = \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, \langle \psi' | \boldsymbol{p}, \sigma \rangle \, \langle \boldsymbol{p}, \sigma | \psi \rangle = \] \[ = \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, [f'_\sigma(\boldsymbol{p})]^* \, f_\sigma(\boldsymbol{p}) \] Dabei ist \( \frac{|f_\sigma(\boldsymbol{p})|^2}{2 p^0} \) die Impuls-Wahrscheinlichkeits-Dichte für vorgegebenes \(\sigma\).
|
Diese Konventionen und Normierungen sind analog gewählt zu Sexl, Urbantke: Relativität, Gruppen, Teilchen, spezielle Relativitätstheorie als Grundlage der Feld- und Teilchenphysik, Springer-Verlag 1992. Steven Weinberg verwendet in seinem Buch The Quantum Theory of Fields, Vol. 1, Kapitel 2.5 andere Konventionen.
Die Formeln gelten auch für Masse Null. Für \(\boldsymbol{p} = 0\) wird dabei allerdings \(p^0 = 0\). Wegen der Division durch \(p^0\) müsste man daher formal den Nullpunkt im Integrationsgebiet ausschließen. Da ein Punkt den Wert des Integrals nicht beeinflusst (ist ja eine Menge vom Maß Null), können wir das problemlos tun.
Nun zu unserer Normierungsfunktion \( N_p \) (wir nehmen an, sie ist reell). Diese Funktion müsste nun festliegen, denn wir haben ja die Normierung \[ \langle \boldsymbol{p}', \sigma' | \boldsymbol{p}, \sigma \rangle = 2p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \, \delta_{\sigma,\sigma'} \] bereits oben festgelegt. Schauen wir uns zum Vergleich die folgende Formel von oben an, wobei wir für den räumlichen Anteil des Vierervektors \(\Lambda p\) die Schreibweise \(\Lambda \boldsymbol{p}\) und für den Energie-Anteil die Schreibweise \( (\Lambda p)^0 \)verwenden wollen, d.h. \[ \Lambda p =: \begin{pmatrix} (\Lambda p)^0 \\ \Lambda \boldsymbol{p} \end{pmatrix} \] Damit haben wir von oben \[ T_g \, |\boldsymbol{p}, \sigma \rangle = \] \[ = \frac{N_p}{N_{\Lambda p}} \, \sum_{\sigma'} \, | \Lambda \boldsymbol{p}, \sigma' \rangle \, D_{\sigma' \sigma}(u) \] Nun soll \( T_g \) unitär sein, d.h. es soll \( T_g^+ T_g = 1 \) sein. Damit folgt aus der Normierung: \[ 2p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \, \delta_{\sigma, \sigma'} = \] \[ = \langle \boldsymbol{p}', \sigma' | \boldsymbol{p}, \sigma \rangle = \] \[ = \langle T_g \, \boldsymbol{p}', \sigma' | T_g \, \boldsymbol{p}, \sigma \rangle = \] \[ = \frac{N_{p'}}{N_{\Lambda p'}} \, \sum_{\alpha'} \, \langle \Lambda \boldsymbol{p}', \alpha' | \, [D_{\alpha' \sigma'}(u)]^* \, \cdot \] \[ \cdot \, \frac{N_p}{N_{\Lambda p}} \, \sum_\alpha \, | \Lambda \boldsymbol{p}, \alpha \rangle \, D_{\alpha \sigma}(u) = \] \[ = \frac{N_{p'}}{N_{\Lambda p'}} \, \frac{N_p}{N_{\Lambda p}} \, \sum_{\alpha', \alpha} \, \langle \Lambda \boldsymbol{p}', \alpha' | \Lambda \boldsymbol{p}, \alpha \rangle \, \cdot \] \[ \cdot \, [D_{\sigma' \alpha'}(u)]^+ \, D_{\alpha \sigma}(u) = \] \[ = \frac{N_{p'}}{N_{\Lambda p'}} \, \frac{N_p}{N_{\Lambda p}} \, \sum_{\alpha', \alpha} \, 2 (\Lambda p)^0 \, \delta^3(\Lambda \boldsymbol{p}' - \Lambda \boldsymbol{p}) \, \cdot \] \[ \cdot \, \delta_{\alpha',\alpha} \, [D_{\sigma' \alpha'}(u)]^+ \, D_{\alpha \sigma}(u) = \] \[ = \left( \frac{N_p}{N_{\Lambda p}} \right)^2 \, \sum_\alpha \, 2 (\Lambda p)^0 \, \delta^3(\Lambda \boldsymbol{p}' - \Lambda \boldsymbol{p}) \, \cdot \] \[ \cdot \, [D_{\sigma' \alpha}(u)]^+ \, D_{\alpha \sigma}(u) \] Schauen wir uns die Delta-Funktion an: Es gilt
| \[ 2 (\Lambda p)^0 \, \delta^3(\Lambda \boldsymbol{p}' - \Lambda \boldsymbol{p}) = \] \[ = 2 p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \] |
Es ist nämlich einerseits (Gleichung (*): \[ f(\boldsymbol{p}') = \] \[ = \int \frac{d^3p}{2 p^0} \, 2 p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \, f(\boldsymbol{p}) \] Andererseits ist \[ f(\boldsymbol{p}') = \] \[ = \int \frac{d^3k}{2 k^0} \, 2 k^0 \, \delta^3(\Lambda \boldsymbol{p}' - \boldsymbol{k}) \, f(\Lambda^{-1} \boldsymbol{k}) = \] ... wir setzen \( k = \Lambda p \) und verwenden die Invarianz des Integrationsmaßes (Gleichung (**)): \[ = \int \frac{d^3p}{2 p^0} \, 2 (\Lambda p)^0 \, \delta^3(\Lambda \boldsymbol{p}' - \Lambda \boldsymbol{p}) \, f(\boldsymbol{p}) \] Vergleich von (*) und (**) ergibt die gewünschte Gleichung. Setzen wir diese Gleichung nun oben ein, so erhalten wir: \[ 2p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \, \delta_{\sigma,\sigma'} = \] \[ \left( \frac{N_p}{N_{\Lambda p}} \right)^2 \, 2 p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \, \cdot \] \[ \cdot \, \sum_{\alpha} \, [D_{\sigma' \alpha}(u)]^+ \, D_{\alpha \sigma}(u) \] Wir setzen \( N_p = N_{\Lambda p} = 1 \) (Weinberg macht das anders!), so dass \[ \sum_\alpha \, [D_{\sigma' \alpha}(u)]^+ \, D_{\alpha \sigma}(u) = \delta_{\sigma, \sigma'} \] oder in Matrixschreibweise \[ D(u)^+ \, D(u) = 1 \] sein muss. Die Darstellungsmatrix \( D(u) \) der kleinen Gruppe muss also bei unserer Normierungskonvention eine unitäre Matrix sein! Unser Ergebnis lautet also:
|
Unitäre Einteilchen-Darstellung der Poincarégruppe:
\[
T_g \, | \boldsymbol{p}, \sigma \rangle
= \]
\[ =
\sum_{\sigma'} \, | \Lambda \boldsymbol{p}, \sigma' \rangle \,
D_{\sigma' \sigma}(u)
\]
mit einer unitären impulsabhängigen Matrix \( D(u) \) als Darstellungsmatrix der kleinen Gruppe.
Das so definierte \(T_g\) ist eine unitäre Darstellung der Überlagerungsgruppe
\(SL(2,\mathbb{C})\), wobei wir die Normierung
\[
\langle \boldsymbol{p}', \sigma' | \boldsymbol{p}, \sigma \rangle
=
\]
\[
= 2 p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p})
\, \delta_{\sigma,\sigma'}
\]
voraussetzen.
Die Darstellung der Raum-Zeit-Translationen \(h(a)\) hatten wir weiter oben schon kennengelernt:
\[
T_{h(a)} \, | \boldsymbol{p}, \sigma \rangle =
\]
\[ =
e^{i \, g(a,\hat{P})} \, | \boldsymbol{p}, \sigma \rangle
=
\]
\[ =
e^{i \, g(a,p)} \, | \boldsymbol{p}, \sigma \rangle
\]
mit der Minkowski-Metrik \(g(a,p)\).
|
Wichtig ist dabei, dass \(D(u)\) vom Impuls \(\boldsymbol{p}\) abhängt, denn \(u\) hängt von \(\boldsymbol{p}\) ab!
Zwar ist \(D(u)\) eine endlich-dimensionale unitäre Darstellung der kleinen Gruppe, aber das ergibt keine endlich-dimensionale unitäre Darstellung der Gruppe \(SL(2,\mathbb{C})\), sondern wegen der \(\boldsymbol{p}\)-Abhängigkeit eine unendlich-dimensionale unitäre Darstellung. Genau deshalb können wir auch nicht \(D(g)\) schreiben. Tatsächlich kann man zeigen, dass es (abgesehen von der trivialen Darstellung durch die Identität) keine endlich-dimensionalen unitären Darstellungen der Gruppe \(SL(2,\mathbb{C})\) und damit auch der Lorentzgruppe gibt! Die obige Darstellung ist wegen der Impulsabhängigkeit unendlich-dimensional.
Bei der kompakten Drehgruppe ist das anders, wie wir am Schluss von Kapitel 4.8 gesehen haben. Mit Hilfe der Kugelflächenfunktionen und Integration über den Winkelanteil von \(\boldsymbol{p}\) lassen sich dort Vektoren bilden, die sich wie die Basisvektoren eines Tensorproduktes bei Drehungen verhalten. Mit Hilfe der Clebsch-Gordan-Koeffizienten lassen sich dann endlich-dimensionale ausreduzierte Darstellungen der Drehungen bilden. Das geht bei den Lorentztransformationen so offenbar nicht. Darin spiegelt sich wieder, dass die Lorentzgruppe und ihre Überlagerungsgruppe wegen der Boosts nicht-kompakt sind.
Wie bei der Drehgruppe in Kapitel 4.8 können wir nun auch unitäre Darstellungen auf Funktionen des Impulses und des Ortes definieren. Die Rechnung verläuft vollkommen analog zu der entsprechenden Rechnung bei der Drehgruppe. Ausgangspunkt ist die Formel (siehe oben) \[ | \psi \rangle = \] \[ = \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, f_\sigma(\boldsymbol{p}) \, | \boldsymbol{p}, \sigma \rangle \] Anwendung von \( T_g \) ergibt: \[ T_g \, |\psi\rangle = \] \[ = \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, f_\sigma(\boldsymbol{p}) \, T_g \, |\boldsymbol{p},\sigma\rangle = \] \[ = \sum_\sigma \int \frac{d^3p}{2 p^0} \, f_\sigma(\boldsymbol{p}) \, \cdot \] \[ \cdot \, \sum_{\sigma'} \, |\Lambda\boldsymbol{p}, \sigma' \rangle \, D_{\sigma' \sigma}(u) = \, ... \] Wir substituieren nun die Integrationsvariable \[ \boldsymbol{p}' := \Lambda \boldsymbol{p} \] und lassen den Strich wieder weg. Dabei verwenden wir die Invarianz des Integrationsmaßes. Vorsicht: \(u\) ist impulsabhängig: \[ u = g(\Lambda p)^{-1} \, g \, g(p) \] Daraus wird \[ u' = g(p)^{-1} \, g \, g(\Lambda^{-1}p) \] Anmerkung: Die Matrix \(u'\) entspricht einem Element der kleinen Gruppe, das \(k\) auf die folgende Weise auf sich selbst abbildet: \[ k \rightarrow \Lambda^{-1} p \rightarrow p \rightarrow k \] Außerdem vertauschen wir die Bezeichnungen für \(\sigma'\) und \(\sigma\): \[ ... \, = \sum_{\sigma', \sigma} \, \int \frac{d^3p}{2 p^0} \, \cdot \] \[ \cdot \, f_{\sigma'}(\Lambda^{-1} \boldsymbol{p}) \, |\boldsymbol{p}, \sigma \rangle \, D_{\sigma \sigma'}(u') = \] \[ =: \sum_\sigma \int \frac{d^3p}{2 p^0} \, \cdot \] \[ \cdot \, [T_g f]_\sigma(\boldsymbol{p}) \, |\boldsymbol{p}, \sigma \rangle \]
mit
| \[ [T_g f]_\sigma(\boldsymbol{p}) := \] \[ = \sum_{\sigma'} \, D_{\sigma \sigma'}(u') \, f_{\sigma'}(\Lambda^{-1} \boldsymbol{p}) \] mit \[ u' = g(p)^{-1} \, g \, g(\Lambda^{-1}p) \] |
Diese Formel sieht analog zu der entsprechenden Formel bei den Drehungen aus. Allerdings tritt die unitäre impulsabhängige Matrix \(D(u')\) der kleinen Gruppe auf, nicht aber eine impulsunabhängige Darstellungsmatrix \(D(g)\) der Poincarégruppe selbst.
Wir können aber leicht eine neue Funktion \( F_\sigma(p) \) definieren, bei der das anders ist. Dazu verwenden wir von oben die Formel \( u' = g(p)^{-1} \, g \, g(\Lambda^{-1}p) \) und gehen weiter davon aus, dass es endlich-dimensionale Darstellungsmatrizen \(D(g)\) der Lorentzgruppe gibt, die nicht unbedingt unitär sein müssen (dass das so ist, sehen wir weiter unten). In Matrixschreibweise haben wir dann \[ D(u') = D(g(p))^{-1} \, D(g) \, D(g(\Lambda^{-1} p)) \] Setzen wir dies in die Gleichung oben ein, die wir ebenfalls in Matrixschreibweise schreiben, um die vielen Indices zu vermeiden: \[ [T_g f](\boldsymbol{p}) = \] \[ = D(u') \, f(\Lambda^{-1}\boldsymbol{p}) = \] \[ = D(g(p))^{-1} \, D(g) \, \cdot \] \[ \cdot \, D(g(\Lambda^{-1} p)) \, f(\Lambda^{-1} \boldsymbol{p}) \] Multiplikation von links mit der Matrix \(D(g(p))\) ergibt \[ D(g(p)) \, [T_g f](\boldsymbol{p}) = \] \[ = D(g) \, D(g(\Lambda^{-1} p)) \, f(\Lambda^{-1}\boldsymbol{p}) \] Wir definieren nun \[ F(p) := D(g(p)) \, f(\boldsymbol{p}) \] mit \( p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \). Diese Formel legt es nahe, auf der Funktion \(F\) eine Darstellung folgendermaßen zu definieren: \[ [T_g F](p) := \] \[ = D(g(p)) \, [T_g f](\boldsymbol{p}) = \] \[ = D(g) \, D(g(\Lambda^{-1} p)) \, f(\Lambda^{-1}\boldsymbol{p}) = \] \[ = D(g) \, F(\Lambda^{-1}p) \] Die rechte Seite zeigt, dass wir so tatsächlich eine Darstellung der Lorentzgruppe (genauer von \(SL(2,\mathbb{C})\) definiert haben. Man spricht auch von der Darstellung auf Feldern. Fassen wir zusammen:
|
Von der unitären Darstellung zur Darstellung auf Feldern: Die unitäre Darstellung \[ [T_g f](\boldsymbol{p}) = D(u') \, f(\Lambda^{-1}\boldsymbol{p}) \] mit der Impuls-abhängigen Wigner-Rotation \( u' = g(p)^{-1} \, g \, g(\Lambda^{-1}p) \) und der unitären Matrix \(D(u')\) liefert über die Definitionen \[ F(p) := D(g(p)) \, f(\boldsymbol{p}) \] \[ [T_g F](p) := D(g(p)) \, [T_g f](\boldsymbol{p}) \] (mit \( p^0 = \sqrt{m^2 + \boldsymbol{p}^2}\) ) die Darstellung \[ [T_g F](p) = D(g) \, F(\Lambda^{-1}p) \] auf den sogenannten Feldern \(F(p)\). Die Darstellungsmatrix \(D(g)\) muss für allgemeine \(g \in SL(2,\mathbb{C})\) nicht unitär sein. |
Wie sieht es mit der Interpretation aus? Erinnern wir uns: Wegen der Normierung \[ \langle \boldsymbol{p}', \sigma' | \boldsymbol{p}, \sigma \rangle = \] \[ = 2p^0 \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \, \delta_{\sigma, \sigma'} \] und der Definition \[ | \psi \rangle = \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, f_\sigma(\boldsymbol{p}) \, |\boldsymbol{p}, \sigma \rangle \] (d.h. \( f_\sigma(\boldsymbol{p}) = \langle \boldsymbol{p}, \sigma | \psi \rangle \) ) ist \[ \frac{|f_\sigma(\boldsymbol{p})|^2}{2 p^0} \] die Impuls-Wahrscheinlichkeits-Dichte und \[ \langle \psi' | \psi \rangle = \] \[ \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, \langle \psi' | \boldsymbol{p}, \sigma \rangle \, \langle \boldsymbol{p}, \sigma | \psi \rangle = \] \[ = \sum_\sigma \, \int \frac{d^3p}{2 p^0} \, [f '_\sigma(\boldsymbol{p})]^* \, f_\sigma(\boldsymbol{p}) \] das Skalarprodukt.
Umgeschrieben mit \(F(p)\) ist demnach \[ \frac{|(D(g(p))^{-1} \, F(p))_\sigma|^2}{2 p^0} \] die Impuls-Wahrscheinlichkeits-Dichte und \[ \langle \psi' | \psi \rangle = \] \[ = \int \frac{d^3p}{2 p^0} \, [D(g(p))^{-1} F'(p)]^+ \, \cdot \] \[ \cdot \, D(g(p))^{-1} F(p) = \] \[ = \int \frac{d^3p}{2 p^0} \, F'(p)^+ \, [D(g(p))^{-1}]^+ \, \cdot \] \[ \cdot \, D(g(p))^{-1} F(p) \] das Skalarprodukt.
Für eine nicht-unitäre Matrix \( D(g(p))^{-1} \) fällt das Matrixprodukt nicht weg und das Skalarprodukt hat eine recht komplizierte Gestalt, wenn man es durch die Felder \(F(p)\) ausdrückt. Für \(F(p)\) gilt also ein einfaches Transformationsgesetz bei Poincarétransformationen, aber es geht auf komplizierte Weise in das Skalarprodukt ein. Das wird uns bei der Betrachtung der Klein-Gordon-Gleichung und der Diracgleichung wieder begegnen.
Da die Wigner-Rotation \( u' \) impulsabhängig ist, liefert eine Fouriertransformation von \(f(\boldsymbol{p})\) kein einfaches Transformationsgesetz für die so gebildete ortsabhängige Funktion. Man kann aber für die Felder \(F(p)\) eine solche Fouriertransformation durchführen, die zu einem einfachen Transformationsgesetz für das Fourier-transformierte Feld führt: \[ \psi(x) := \] \[ = N \, \int d^4p \, F(p) \, e^{- i p x} \, \cdot \] \[ \cdot \, \delta(p^2 - m^2) \, \Theta(p^0) = \] \[ = N \, \int \frac{d^3p}{2 p^0} \, F(p^0,\boldsymbol{p}) \, e^{- i p^0 t} \, e^{i \boldsymbol{p x}} \] mit \( p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \) in der unteren Zeile, der Normierung \(N = (2π)^{-3/2}\) und der Minkowski-Metrik \( p x = g(p,x) \). Die Delta-Funktion sorgt wie oben dafür, dass nur Impulse zur gleichen Masse \(m\) überlagert werden, und die Theta-Funktion sorgt dafür, dass \(p^0 \ge 0\) sein muss. Analog zu unserer Vorgehensweise bei den Drehungen und den Translationen definieren wir: \[ [T_g \psi](x) := \] \[ = N \, \int d^4p \, [T_g F](p) \, e^{- i p x} \, \cdot \] \[ \cdot \, \delta(p^2 - m^2) \, \Theta(p^0) = \] \[ = N \, \int d^4p \, D(g) \, F(\Lambda^{-1} p) \, e^{- i p x} \, \cdot \] \[ \cdot \, \delta(p^2 - m^2) \, \Theta(p^0) = \, ... \]
wir setzen \( p' := \Lambda^{-1} p \) und verwenden \( d^4p = d^4p' \) sowie \((p')^2 = p^2 \) (Minkowskimetrik!), \( \Theta(p'^0) = \Theta(p^0) \) (keine Zeitspiegelungen!) und \( (\Lambda p') x = p' (\Lambda^{-1} x) \) (invariante Minkowskimetrik!) \[ ... \, = N \, \int d^4p' \, D(g) \, F(p') \, e^{- i p' (\Lambda^{-1} x)} \, \cdot \] \[ \cdot \, \delta(p' ^2 - m^2) \, \Theta(p' ^0) = \] \[ = D(g) \, \psi(\Lambda^{-1} x) \] Wir können auch noch zusätzlich Raum-Zeit-Translationen \(h(a)\) berücksichtigen, indem wir \( T_{g,a} := T_g \, T_{h(a)} \) setzen. In der obigen Rechnung müssen wir dann \( e^{- i p x} \) durch \( e^{- i p x} \, e^{i p a} \) ersetzen mit dem Ergebnis:
| Darstellung auf Feldern im Ortsraum: \[ [T_{g,a} \psi](x) = D(g) \, \psi(\Lambda^{-1}(x - a)) \] |
Diese Formel entspricht genau der Vorstellung davon, wie sich eine Orts-Zeit-abhängige Funktion bei einer Poincarétransformation verhalten sollte. Dies rechtfertigt auch die Interpretation von \(x\) als Raum-Zeit-Vierervektor.
Allerdings können wir das Feld \( \psi(x) \) nicht als Amplitude für die Aufenthaltswahrscheinlichkeit des Teilchens interpretieren – anders als in der nichtrelativistischen Quantentheorie, bei der die Division durch \(2 p^0 \) im Integrationsmaß nicht notwendig ist, um ein invariantes Integrationsmaß zu erhalten. Erst die relativistischen Boosts machen das notwendig.
Welche Größe aber könnte man – zumindest im Prinzip – als Aufenthaltswahrscheinlichkeit eines Teilchens interpretieren? Die Antwort kennen wir aus der nichtrelativistischen Quantenmechanik: Wir brauchen die (gewöhnliche) dreidimensionale Fouriertransformation der Impuls-Wahrscheinlichkeitsamplitude. Diese war gegeben durch \( \frac{|f_\sigma(\boldsymbol{p})|^2}{2p^0} \). Die entsprechende fouriertransformierte Größe \(\Psi(x)\) (nicht \(\psi(x)\)) ist dann gegeben durch \[ \Psi_\sigma(\boldsymbol{x}) := N \, \int d^3p \, \frac{f_\sigma(\boldsymbol{p})}{\sqrt{2p^0}} e^{i \boldsymbol{p x}} \] mit \( N = (2 \pi)^{-3/2}\). Warum diese Größe sich als Wahrscheinlichkeitsdichten-Amplitude eignet, sehen wir am Skalarprodukt. Es ist nämlich in Matrixschreibweise \[ \int d^3x \, \Psi(\boldsymbol{x})^+ \, \Psi(\boldsymbol{x}) = \] \[ = N^2 \, \int d^3x \, \int d^3p' \, \int d^3p \, \] \[ \frac{f(\boldsymbol{p}')^+}{\sqrt{2p'^0)}} \, e^{-i \boldsymbol{p' x}} \, \frac{f(\boldsymbol{p})}{\sqrt{2p^0)}} \, e^{i \boldsymbol{p x}} = \] \[ = N^2 \, \int d^3p' \, \int d^3p \, \cdot \] \[ \frac{f(\boldsymbol{p}')^+ \, f(\boldsymbol{p})}{\sqrt{2p'^0} \sqrt{2p^0)}} \, \int d^3x \, e^{i (\boldsymbol{p} - \boldsymbol{p}') \boldsymbol{x}} = \] \[ = N^2 \, \int d^3p' \, \int d^3p \, \frac{f(\boldsymbol{p}')^+ \, f(\boldsymbol{p})}{\sqrt{2p'^0} \sqrt{2p^0}} \, \cdot \] \[ \int d^3x \, (2 \pi)^3 \, \delta^3(\boldsymbol{p} - \boldsymbol{p}') = \] \[ = \int d^3p \, \frac{f(\boldsymbol{p})^+ \, f(\boldsymbol{p})}{2p^0} = \] \[ = \langle \psi | \psi \rangle = 1 \] wobei wir die Formel \[ \int d^3x \, e^{i (\boldsymbol{p} - \boldsymbol{p}') \boldsymbol{x}} = (2 \pi)^3 \, \delta^3(\boldsymbol{p} - \boldsymbol{p}') \] verwendet haben (siehe Wikipedia: Delta-Distribution ). Nach dem, was wir oben über sie Wahrscheinlichkeitsdichte einer kontinuierlichen Zufallsgröße gelernt haben, wäre \[ \Psi(\boldsymbol{x})^+ \, \Psi(\boldsymbol{x}) \] ein Kandidat für eine solche Wahrscheinlichkeitsdichte der Zufallsgröße \(\boldsymbol{x}\), die wir als Teilchenort interpretieren wollen. Genau so kennen wir das aus der nichtrelativistischen Quantenmechanik, und so muss es auch in der relativistischen Quantenmechanik sein.
Wir können die Orts-Wahrscheinlichkeitsamplitude \( \Psi(\boldsymbol{x})\) durch das Feld \(\psi(0,\boldsymbol{x})\) ausdrücken (zur Vereinfachung wählen wir \(t = 0\) ): \[ \Psi(\boldsymbol{x}) = \] \[ = N \, \int d^3p \, \frac{f(\boldsymbol{p})}{\sqrt{2p^0}} e^{i \boldsymbol{p x}} = \] \[ = N \, \int d^3p \, \frac{D(g(p))^{-1} \, F(p)}{\sqrt{2p^0}} \, e^{i \boldsymbol{p x}} = \] \[ = N \, \int \frac{d^3p}{2 p^0} \, \int d^3p' \, \delta^3(\boldsymbol{p}' - \boldsymbol{p}) \, \cdot \] \[ \cdot \, D(g(p'))^{-1} \, \sqrt{2p'^0} \, F(p) \, e^{i \boldsymbol{p x}} = \] \[ = N \, \int \frac{d^3p}{2 p^0} \, \int d^3p' \, N^2 \, \int d^3x' \, e^{i (\boldsymbol{p}' - \boldsymbol{p} ) \boldsymbol{x'}} \, \cdot \] \[ \cdot \, D(g(p'))^{-1} \, \sqrt{2p'^0} \, F(p) \, e^{i \boldsymbol{p x}} = \] \[ = N \, \int d^3x' \, N \, \int \frac{d^3p}{2 p^0} \, F(p) \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x'} )} \, \cdot \] \[ \cdot \, N \, \int d^3p' \, e^{i \boldsymbol{p}' \boldsymbol{x'}} \, D(g(p'))^{-1} \, \sqrt{2p'^0} = \] \[ = N \, \int d^3x' \, \psi(0, \boldsymbol{x} - \boldsymbol{x'} ) \, \cdot \] \[ \cdot \, N \, \int d^3p' \, e^{i \boldsymbol{p}' \boldsymbol{x'}} \, D(g(p'))^{-1} \, \sqrt{2p'^0} = \] \[ = N \, \int d^3x' \, \psi(0, \boldsymbol{x} - \boldsymbol{x'} ) \, D(\boldsymbol{x'}) \] mit \[ D(\boldsymbol{x'}) := N \, \int d^3p' \, e^{i \boldsymbol{p}' \boldsymbol{x'}} \, \cdot \] \[ \cdot \, D(g(p'))^{-1} \, \sqrt{2p'^0} \] Orts-Wahrscheinlichkeitsamplitude \(\Psi\) und ortsabhängiges Feld \(\psi\) hängen also über ein Faltungsintegral \[ \Psi(\boldsymbol{x}) = \] \[ = N \, \int d^3x' \, \psi(0, \boldsymbol{x} - \boldsymbol{x'} ) \, D(\boldsymbol{x'}) \] zusammen, d.h. erst das mit \( D(\boldsymbol{x'}) \) verschmierte Feld \(\psi\) ergibt die Orts-Wahrscheinlichkeitsamplitude \( \Psi(\boldsymbol{x}) \).
Dies ist die präzise Version der Außage, dass das Feld \( \psi(0,\boldsymbol{x}) \) nur ungefähr angibt, wo sich das Teilchen aufhalten kann. Wegen dem Faltungsintegral ist die Orts-Wahrscheinlichkeitsamplitude \( \Psi(\boldsymbol{x}) \) insgesamt eine relativ unpraktische Größe in der relativistischen Quantentheorie. Das Feld \(\psi\) ist viel angenehmer zu handhaben, aber nicht unmittelbar zu interpretieren.
Hinzu kommen andere Aspekte: So ist eine beliebig genaue Ortsmessung bei einem Teilchen prinzipiell nicht möglich, da dafür viel Energie auf kleinem Raum konzentriert werden muss, was zur Bildung von neuen Teilchen-Antiteilchen-Paaren führt mit der Folge, dass man oft nicht mehr weiß, welches das ursprüngliche Teilchen war. Auch aus diesem Grund ist es nur begrenzt sinnvoll, überhaupt von dem Aufenthaltsort eines relativistischen Teilchens zu reden. Das ist beim Impuls eines freien Teilchens anders – er lässt sich beliebig genau messen, solange man beliebig viel Messzeit zur Verfügung hat.
Soviel dazu. Bleibt noch die Frage: Wie sehen die Darstellungsmatrizen \(D(u)\) und \(D(g)\) denn nun wirklich aus? Beginnen wir mit \(D(u)\). Wie wir oben bereits gesehen haben, gibt es zwei physikalisch relevante Fälle: \(p^2 \gt 0 \) und \(p^2 = 0\) (und \( p^0 \gt 0 \) in beiden Fällen). Der Standardvektor \(k\) sieht in beiden Fällen verschieden aus, so dass auch die kleine Gruppe jeweils verschieden ist. Beginnen wir mit dem Fall \( p^2 \gt 0 \):
Für \( p^2 = m^2 \gt 0 \) können wir als Standardvektor den Vektor \[ k = \begin{pmatrix} m \\ \boldsymbol{0} \end{pmatrix} \] wählen. Das ist der Viererimpuls eines Teilchens mit Masse \(m\) und räumlichem Impuls Null – das Teilchen ruht also bewegungslos (Ruhesystem).
Die Lorentztransformationen, die \(k\) nicht verändern, sind damit gerade die räumlichen Drehungen (Boosts scheiden ja aus, denn sie würden einen räumlichen Impuls ergeben). Die kleine Gruppe ist also \(SO(3)\), und die entsprechenden \(SL(2,\mathbb{C})\)-Matrizen \(u\) stammen aus der zugehörigen Überlagerungsgruppe \(SU(2)\).
Damit sind auch die Darstellungsmatrizen \(D(u)\) für eine ausreduzierte Darstellung klar: Es handelt sich um die \((2s + 1)\) -dimensionalen \(SU(2)\)-Darstellungsmatrizen \( D^s(u) \) zum Spin \(s\), so wie wir sie in Kapitel 4.8 kennengelernt haben (warum wir hier das Wort Spin verwenden, wird etwas weiter unten noch klar werden). Diese Darstellungsmatrizen sind in geeigneter Basis unitär, so wie wir das oben von \(D(u)\) auch verlangt haben (da die Gruppe \(SU(2)\) kompakt ist, liefern die unitären Darstellungen zugleich sämtliche möglichen Matrixdarstellungen, wenn man die Basis geeignet wählt).
Warum haben wir oben vom Spin gesprochen? In Kapitel 4.8 hatten wir die Spinquantenzahlen \(s\) und \(m_s\) eines Zustandes \( | \boldsymbol{p} s m_s \rangle \) dadurch definiert, dass sich der Zustand bei Drehungen \( T_{u(\boldsymbol{w})} = e^{-i \boldsymbol{w \hat{J}}} \) folgendermaßen transformiert: \[ T_{u(\boldsymbol{w})} \, | \boldsymbol{p} s m_s \rangle = \] \[ = \sum_{m_s'} \, | R(\boldsymbol{w}) \, \boldsymbol{p} , s m_s' \rangle \, D^s_{m_s' m_s}(u(\boldsymbol{w})) \] Dabei haben wir extra \(u(\boldsymbol{w})\) statt \(u\) geschrieben, um die Drehung \(u(\boldsymbol{w})\) von der Wigner-Rotation \(u\) zu unterscheiden. Zum Vergleich: Oben hatten wir für die unitären Einteilchendarstellungen der Poincarégruppe die Gleichung \[ T_g \, |\boldsymbol{p}, \sigma \rangle = \] \[ = \sum_{\sigma'} \, |\Lambda\boldsymbol{p}, \sigma' \rangle \, D_{\sigma' \sigma}(u) \] gefunden mit der Wigner-Rotation \(u := g(\Lambda p)^{-1} \, g \, g(p)\). Diese Formel können wir uns nun für eine Drehung \(g = u(\boldsymbol{w})\) und zugehörigem \( \Lambda \boldsymbol{p} = R(\boldsymbol{w}) \, \boldsymbol{p} \) anschauen. Dabei wählen wir die Basis durch Ausreduktion der Darstellung so, dass \( |\boldsymbol{p}, \sigma \rangle = | \boldsymbol{p} s m_s \rangle \) und \( D_{\sigma' \sigma}(u) = D^s_{m_s' m_s}(u) \) ist: \[ T_{u(\boldsymbol{w})} \, | \boldsymbol{p} s m_s \rangle = \] \[ = \sum_{m_s'} \, | R(\boldsymbol{w}) \, \boldsymbol{p} , s m_s' \rangle \, D^s_{m_s' m_s}(u) \] Das sieht schon fast so aus wie die Spin-Drehungsformel von oben aus Kapitel 4.8. Allerdings steht rechts die Wigner-Rotation \(u\), die zur Drehung \(u(\boldsymbol{w})\) gehört, und nicht die Drehung \(u(\boldsymbol{w})\) selbst. Rechnen wir also die Wigner-Rotation \(u\) zur Drehung \(u(\boldsymbol{w})\) aus. Dazu müssen wir allerdings noch eine weitere Konvention treffen. Die Gleichung \( p = \Lambda_p \, k \) legt nämlich die Lorentz-Transformation \( \Lambda_p \) und das zugehörige \( g(p) \) noch nicht eindeutig fest, so dass auch die Wigner-Rotation noch nicht eindeutig definiert ist. So kann man beispielsweise bei \( k = (m, \boldsymbol{0}) \) erst eine beliebige Drehung und dann einen Boost in \(\boldsymbol{p}\)-Richtung durchführen und erhält jeweils ein gültiges \(\Lambda_p\). Die beliebigen Drehungen wollen wir nun ausschließen. Wir fordern daher, dass \(\Lambda_p\) ein reiner Boost sein muss. Gleichwertig dazu ist die Forderung, dass \(g(p)\) eine hermitesche Matrix sein muss. Erst dadurch ist unsere Basis nach der Formel
| \[ | \boldsymbol{p} s m_s \rangle := T_{g(p)} \, | (m,\boldsymbol{0}), s m_s \rangle \] |
von oben nun eindeutig festgelegt. Mit dieser Konvention können wir die Wigner-Rotation \[ u := g(\Lambda p)^{-1} \, u(\boldsymbol{w}) \, g(p) \] für die Drehung \(u(\boldsymbol{w})\) nun ausrechnen. Das kann man auf verschiedene Art tun. Bereits anschaulich ist am Beispiel von \( k = (m,\boldsymbol{0}) \) klar: \[ R \, p = R \, \Lambda_p (m,\boldsymbol{0}) = \Lambda_{R p} \, R \, (m,\boldsymbol{0}) \] Anhand der Matrizen kann man explizit nachrechnen, dass auch allgemein \[ R \, \Lambda_p = \Lambda_{R p} \, R \] ist. Übersetzt auf die Überlagerungsgruppe bedeutet das: \[ u(\boldsymbol{w}) \, g(p) = g(Rp) \, u(\boldsymbol{w}) \] oder umgestellt \[ u(\boldsymbol{w}) = g(Rp)^{-1} \, u(\boldsymbol{w}) \, g(p) \] Die rechte Seite ist aber gerade unsere Definition der Wigner-Rotation \(u\), so dass wir \[ u = u(\boldsymbol{w}) \] haben. Für eine Drehung ist die Wigner-Rotation gerade identisch mit dieser Drehung. Und damit können wir auch oben \(u(\boldsymbol{w}) = u\) setzen und haben
| \[ T_{u(\boldsymbol{w})} \, | \boldsymbol{p} s m_s \rangle = \] \[ = \sum_{m_s'} \, | R(\boldsymbol{w}) \, \boldsymbol{p} , s m_s' \rangle \, D^s_{m_s' m_s}(u(\boldsymbol{w})) \] |
Das ist genau die Drehvorschrift für Spin-Zustände und liefert die Begründung dafür, den Index \( \sigma = (s, m_s) \) als Spinquantenzahl zu bezeichnen.
Erst wollte ich den masselosen Fall recht kurz abhandeln. Dann aber habe ich festgestellt, dass man später (z.B. bei der Weyl-Gleichung oder bei Eichfeldern mit Spin 1) die Details doch braucht. Es hilft also nichts – schauen wir uns die Details doch genauer an. Es wird dann sogar recht interessant, denn der masselose Fall hält doch einige Überraschungen bereit! Die genaue Analyse findet man übrigens beispielsweise in Steven Weinberg: The Quantum Theory of Fields, Vol. 1, Kapitel 2.5 (ab Seite 69). oder in Hendrik van Hees: Introduction to Relativistic Quantum Field Theory.
Zunächst einmal gibt es für masselose Teilchen kein Ruhesystem, so dass wir nicht \( k = (m, \boldsymbol{0}) \) wählen können (es muss ja \( p^2 = k^2 = 0 \) sein). Stattdessen kann man beispielsweise \[ k = \begin{pmatrix} \kappa \\ \kappa \, \boldsymbol{e}_3 \end{pmatrix} \] verwenden mit einer beliebigen Energie \(\kappa\). Wie üblich setzen wir \( \kappa = 1 \). Anschaulich kann man sich vorstellen, dass \(k\) einen Standardlichtstrahl in z-Richtung mit Photonenergie 1 (in natürlichen Einheiten) darstellt. Dabei sollte man sich keinen dünnen Lichtstrahl vorstellen, sondern ein paralleles Bündel von Lichtstrahlen (auf der Erde liefert das Sonnenlicht annähernd so ein paralleles Lichtbündel, allerdings mit verschiedenen Photonenergien).
Wir suchen also nun die Lorentzmatrizen \(\Lambda_u\), die den Standardlichtstrahl in z-Richtung und somit \(k\) invariant lassen: \[ \Lambda_u \, k = k \] Im Fall mit Masse hatten wir sie als Wigner-Rotationen bezeichnet. Diese Bezeichnung wollen wir auch im masselosen Fall beibehalten, auch wenn \(\Lambda_u\) nun nicht mehr unbedingt eine Rotation sein muss.
Betrachten wir zunächst die Wirkung von \(\Lambda_u\) auf den Zeit-Basisvierervektor \[ e_0 = \begin{pmatrix} 1 \\ \boldsymbol{0} \end{pmatrix} \] d.h. wir interessieren uns für die erste Spalte der Matrix \(\Lambda_u \). Für diese Spalte und damit für den Vektor \( \Lambda_u \, e_0 \) machen wir den Ansatz \[ \Lambda_u \, e_0 = \begin{pmatrix} \gamma \\ \delta \\ \eta \\ \zeta \end{pmatrix} \] mit vier reellen Zahlen \( \gamma, \delta, \eta, \zeta\). Für die Lorentzmetrik \(g\) zwischen \( e_0 = (1, \boldsymbol{0}) \) und \( k = (1, \boldsymbol{e}_3) \) gilt dann (da sie invariant unter Anwendung der Lorentzmatrix \(\Lambda_u\) sein muss): \[ 1 = g(e_0, k) = \] \[ = g(\Lambda_u \, e_0, \Lambda_u \, k) = \] \[ = g(\Lambda_u e_0, k) = \] \[ = \gamma - \zeta \] Es ist also \(1 = \gamma - \zeta \) oder umgestellt \[ \gamma = 1 + \zeta \] Außerdem gilt: \[ 1 = g(e_0, e_0) = \] \[ = g(\Lambda_u e_0, \Lambda_u e_0) = \] \[ = \gamma^2 - \delta^2 - \eta^2 - \zeta^2 = \] \[ = (1 + \zeta)^2 - \delta^2 - \eta^2 - \zeta^2 = \] \[ = 1 + 2\zeta - \delta^2 - \eta^2 \] und somit \[ \zeta = \frac{1}{2} (\delta^2 + \eta^2) \] Insgesamt ist also \[ \Lambda_u \, e_0 = \begin{pmatrix} 1 + \zeta \\ \delta \\ \eta \\ \zeta \end{pmatrix} \] mit \( \zeta = \frac{1}{2} (\delta^2 + \eta^2) \).
Damit kennen wir nun die erste Spalte der Matrix \(\Lambda_u\), denn diese ist ja gerade gleich \(\Lambda_u \, e_0 \). Eine (nicht unbedingt mit \(\Lambda_u\) identische) Lorentzmatrix \( \Lambda_N(\delta,\eta) \), die auch diese erste Spalte besitzt, ist \[ \Lambda_N(\delta,\eta) = \]
(siehe z.B. Alejandro Jenkins: Topics in Theoretical Particle Physics and Cosmology Beyond the Standard Model, Kapitel 2.2.3). Wir bezeichnen \( \Lambda_N(\delta,\eta) \) oder auch abgekürzt \(\Lambda_N\) als Nulldrehung, was schon mal das tiefergestellte \(N\) in der Bezeichnung erklärt – mehr dazu später.
Da \( \Lambda_u \) und \( \Lambda_N \) beide dieselbe erste Spalte besitzen, ist natürlich \[ \Lambda_u \, e_0 = \Lambda_N \, e_0 \] (dieser Vektor ist ja die erste Spalte). Wir multiplizieren diese Gleichung von links mit \( \Lambda_N^{-1} \) und erhalten \[ \Lambda_N^{-1} \, \Lambda_u \, e_0 = e_0 \] Die Lorentztransformation \( \Lambda_N^{-1} \, \Lambda_u \) verändert also den Zeitvektor \( e_0 = (1, \boldsymbol{0}) \) nicht. Die einzigen Lorentztransformationen, die das tun, sind die Drehungen (nicht aber die Boosts), d.h. \( \Lambda_N^{-1} \, \Lambda_u \) ist eine Drehung.
Außerdem ist \( \Lambda_N \) genau wie \( \Lambda_u \) eine Wigner-Rotation, lässt also den Standardvektor \( k = (1, \boldsymbol{e}_3) \) unverändert (das kann man der Matrix \( \Lambda_N \) sofort ansehen, denn \( \Lambda_N \, k \) ist gleich der ersten Spalte plus der vierten Spalte dieser Matrix).
Damit muss auch die Drehung \( \Lambda_N^{-1} \, \Lambda_u \) als Produkt zweier Wigner-Rotationen ebenfalls eine Wigner-Rotation sein – sie lässt den Standardlichtstrahl in z-Richtung also unverändert. Das tun aber nur die Drehungen um die z-Achse, die wir mit \( R(\varphi) \) bezeichnen wollen. Es ist also \[ \Lambda_N(\delta,\eta)^{-1} \, \Lambda_u = R(\varphi) \] oder nach \( \Lambda_u \) freigestellt \[ \Lambda_u = \Lambda_N(\delta,\eta) \, R(\varphi) \] Halten wir dieses wichtige Ergebnis fest:
|
Die kleine Gruppe bei masselosen Teilchen: Zur Festlegung der kleinen Gruppe für Masse Null wählen wir als Standardimpuls den Vektor \[ k = \begin{pmatrix} 1 \\ \boldsymbol{e}_3 \end{pmatrix} \] (Lichtstrahl mit Energie 1 in natürlichen Einheiten in z-Richtung). Die kleine Gruppe umfasst alle Lorentzmatrizen \(\Lambda_u\), die diesen Lichtstrahl nicht verändern, d.h. es gilt \[ \Lambda_u \, k = k \] Dann kann man jedes \(\Lambda_u\) dieser kleinen Gruppe als eine Drehung \(R(\varphi)\) um die \(\boldsymbol{k}\)-Achse (hier die z-Achse) und eine anschließende Nulldrehung \(\Lambda_N(\delta,\eta)\) schreiben: \[ \Lambda_u = \Lambda_N(\delta,\eta) \, R(\varphi) \] mit der oben angegebenen Nulldrehungs-Matrix \( \Lambda_N(\delta,\eta) \). |
Die Drehungen \( R(\varphi) \) um die z-Achse sind uns gut vertraut. Schauen wir uns daher die Nulldrehungen (die auch lichtartige Drehungen genannt werden) genauer an. Die Lorentzmatrix \( \Lambda_N(\delta,\eta) \) für diese Nulldrehungen hatten wir oben bereits angegeben.
Zunächst wollen wir versuchen, anschaulich zu verstehen, was Nulldrehungen sind und warum es sie überhaupt gibt. Man könnte ja zunächst meinen, die einzigen Lorentztransformationen, die einen Lichtstrahl in z-Richtung mit Photonen-Energie 1 (also \( k = (1, \boldsymbol{e}_3) \) ) unverändert lassen, seien die Drehungen um die z-Achse. Es gibt aber noch weitere Lorentztransformationen, die den Lichtstrahl invariant lassen und die man wie alle Lorentztransformationen aus einem Boost und anschließender Drehung zusammensetzen kann. Überlegen wir uns, wie dieser Boost und diese Drehung aussehen könnten, so dass sich \(k\) nicht ändert.
Dazu wählen wir zunächst irgendeine beliebige Boostrichtung \(\boldsymbol{e}\) aus und führen einen Boost mit Boost-Geschwindigkeit \( \boldsymbol{u} = u \, \boldsymbol{e} \) in diese Richtung durch – wir bewegen uns (wenn wir vor dem Boost ruhen) also nach dem Boost mit der Boost-Geschwindigkeit \(u\), wobei diese auch negativ sein kann (Boost in die umgekehrte \(\boldsymbol{e}\)-Richtung; Achtung: \(u\) ist hier kein Gruppenelement, sondern eine Geschwindigkeit!).
Lichtstrahlen, die von vorne auf uns zukommen, sehen wir dann blauverschoben, also mit größerer Energie als zuvor. Lichtstrahlen, die von hinten auf uns zukommen, sehen wir dagegen rotverschoben, also mit geringerer Energie als zuvor. Und der Standardlichtstrahl mit Photonimpuls \(k\), der irgendwie schräg auf uns zukommt – wie sehen wir ihn?
Er scheint nach dem Boost mehr von vorne auf uns zuzukommen als zuvor – man nennt das Aberration. Und er könnte nach dem Boost irgendeine Energie zwischen maximal rotverschoben und maximal blauverschoben besitzen. Wenn wir die Boostgeschwindigkeit \(u\) passend wählen, können wir bei vorgegebener Boostrichtung \(\boldsymbol{e}\) immer erreichen, dass seine Energie sich überhaupt nicht ändert – weder rot- noch blauverschoben.
Dabei müssen wir das Vorzeichen von \(u\) so wählen, dass der Standard-Lichtstrahl vor dem Boost eher von hinten auf uns zukommt, nach dem Boost aber aufgrund der Aberration eher von vorne. Es ist sogar so: Wenn der Standard-Lichtstrahl vor dem Boost einen Winkel \(\psi\) mit der Rückwärts-Richtung einschließt, so muss er nach dem Boost mit der Vorwärtsrichtung denselben Winkel \(\psi\) einschließen – genau so müssen wir \(u\) bei gegebener Richtung \boldsymbol{e} wählen.
Die Energie des Standard-Lichtsstrahls ändert sich dabei überhaupt nicht, wohl aber seine Richtung. Wir können die alte Richtung aber nun durch eine anschließende Rotation wiederherstellen und haben damit eine Nulldrehung hinter uns, die den Standardlichtstrahl nicht verändert. Diese Vorgehensweise funktioniert für beliebige Boostrichtungen. Als Parameter der Nulldrehung können wir den Winkel \(\varphi\) wählen, den die Boostrichtung \(\boldsymbol{e}\) in Kugelkoordinaten projeziert auf die x-y-Ebene relativ zur x-Achse besitzt, sowie die Boost-Rapidität \(\alpha\), die zugleich den Winkel \(\psi\) zwischen \(\boldsymbol{e}\) und der z-Achse festlegt. \(\varphi\) und \(\alpha\) können wir dann im Wesentlichen als Polarkoordinaten (Winkel und Radius) in der \(\delta\) - \(\eta\) -Ebene auffassen und so in die karthesischen Parameter \(\delta\) und \(\eta\) umrechnen (vgl. Greg Egan: Re: Measurement and Observers).
Man sieht also: Auch anschaulich ist klar, dass es Nulldrehungen gibt.
Mehr dazu im Internet beispielsweise unter
Greg Egan: Null Rotations in 2+1 dimensions
sowie
Greg Egan: Re: Measurement and Observers.
Auch Wikipedia: Lorentz group
sagt Einiges über Nulldrehungen.
Zu diesem Bild:
Situation vor dem Boost, der nach oben stattfinden wird. Unser Standardlichtstrahl kommt von links unten – die z-Achse zeigt also nach rechts oben. Der Lichtstrahl schließt mit der Rückwärtsrichtung einen Winkel \(\psi\) ein.
Situation nach dem Boost nach oben. Lichtstrahlen von vorne sind blauverschoben (blauer Pfeil), Lichtstrahlen von hinten sind rotverschoben (roter Pfeil). Unser Standardlichtstrahl kommt nun aufgrund der Aberration schräg von vorne. Die Boostgeschwindigkeit wurde dabei so gewählt, dass seine Energie genau zwischen rot- und blauverschoben liegt, so dass sie sich nicht geändert hat. Bei dieser Boostgeschwindigkeit schließt der Standardlichtstrahl nun mit der Vorwärtsrichtung genau denselben Winkel \(\psi\) ein wie zuvor mit der Rückwärtsrichtung.
Wir drehen unseren Standardlichtstrahl zum Schluss wieder in die Ursprungsrichtung. Damit sieht unser Standardlichtstrahl wieder genauso aus wie zuvor. Die anderen Lichtstrahlen haben sich dagegen verändert (roter und blauer Pfeil).
Wie sieht die Gruppenstruktur der kleinen Gruppe bei Masse Null aus?
Bei der Multiplikation zweier Nulldrehungen addieren sich
die zugehörigen reellen Parameter \(\delta\) und \(\eta\) der beiden Nulldrehungen,
so wie das die Verschiebungsvektoren bei Translationen tun.
Insgesamt findet man, dass sich die kleine Gruppe bei masselosen Teilchen
genauso verhält wie die
Gruppe \(ISO(2)\) der Drehungen und Translationen in einer zweidimensionalen reellen
Ebene, wobei \(\delta\) und \(\eta\)
das Analogon der Translationsparameter sind (dieser zweidimensionale Raum hängt aber nur
indirekt mit der Raumzeit zusammen, siehe oben).
Zu den Nulldrehungen gehören daher analog zum Impuls zwei kontinuierliche Quantenzahlen, die die Eigenwerte der Nulldrehungs-Generatoren sind (Details siehe z.B. Steven Weinberg: The Quantum Theory of Fields, Vol. 1). Allerdings treten in der Natur solche kontinuierlichen Quantenzahlen bei masselosen Teilchen nicht auf, so dass wir diese bei physikalisch relevanten Zuständen gleich Null setzen müssen. Der physikalische Zustand \( |\boldsymbol{p}, \sigma \rangle \) enthält nur die sogenannte Helizität \(\sigma\), die sich bei Drehungen um die z-Achse auswirkt, aber keine kontinuierlichen Nulldrehungs-Quantenzahlen. Die Nulldrehungen spielen also bei der Darstellungsmatrix \(D(u)\) der kleinen Gruppe keine Rolle. Auf den Impuls des Zustandes wirken sie sich dagegen aus, wie jede andere Lorentztransformation auch. Die Matrix \(D(u)\) ist also eine Darstellungsmatrix für die Drehung \(R(\varphi)\) um die z-Achse, die in der Wigner-Rotation enthalten ist. Diese Darstellungsmatrix lautet \[ D_{\sigma' \sigma}(u) = e^{-i \varphi \sigma} \, \delta_{\sigma' \sigma} \] mit der Helizität \(\sigma\) (eine Zahl, keine Pauli-Matrix!) im Exponenten. Wir haben also:
| \[ T_g \, | \boldsymbol{p}, \sigma \rangle = | \Lambda \boldsymbol{p}, \sigma \rangle \, e^{-i \varphi \sigma} \] |
mit einem Drehwinkel \(\varphi\), der wie \(u\) von \(g\) und \(p\) abhängt, sowie einer reellen Zahl \(\sigma\), die wir als Helizität bezeichnet haben (Vorsicht: nicht mit den Pauli-Matrizen verwechseln!). Man kann sich vorstellen, dass die Helizität die Spinkomponente in Bewegungsrichtung ist (Begründung kommt später).
Von der Lie-Algebra der kleinen Gruppe her könnte \(\sigma\) eine beliebige reelle Zahl sein – aus Kapitel 4.6 wissen wir ja, dass der Spin in 2 Dimensionen nicht quantisiert ist (Stichwort Anyonen). Klar: Die Lie-Algebra der Drehungen um die z-Achse hat nur einen Generator, so dass es keine Nebenbedingungen wie bei den dreidimensionalen Drehungen gibt, die bestimmte Drehimpulswerte erzwingen.
Da aber \(T_g\) eine Darstellung von \(SL(2,\mathbb{C})\) sein soll, kann \(\sigma\) wie jede andere Drehimpulskomponente nur halb- und ganzzahlige positive und negative Werte inclusive Null annehmen. Man sagt, die Helizität ist quantisiert. Erst wenn wir also die kleine Gruppe als Untergruppe von \(SL(2,\mathbb{C})\) verstehen und nach der entsprechenden Untergruppe der Darstellungsmatrizen von \(SL(2,\mathbb{C})\) fragen, ergibt sich eine Bedingung für die Quantisierung der Helizität.
Außerdem zeigt die obige Formel, dass sich bei Lorentztransformationen (ohne Spiegelungen) die Helizität nicht ändert (anders als die Drehimpulskomponente eines massiven Teilchens). Das hängt damit zusammen, dass man ein masseloses Teilchen nicht überholen kann. Die Phase eines masselosen Zustandes ändert sich bei Lorentztransformationen aber sehr wohl in Abhängigkeit von der Helizität – das merkt man beispielsweise bei der Superposition von Zuständen entgegengesetzter Helizität, z.B. bei polarisiertem Licht.
Nulldrehungen gehen bei masselosen Zuständen also nicht in die Darstellungsmatrix \(D(u)\) der kleinen Gruppe ein – so erfordert es die physikalische Realität, die wir vorfinden (die Mathematik erzwingt das dagegen so nicht). Wenn wir nun zu Impulsamplituden und weiter zu Feldern übergehen, so wird sich diese Forderung in Nebenbedingungen für die Felder niederschlagen. Für Vektorfelder ergeben sich so beispielsweise die sogenannten Eichbedingungen. Man sieht, wie eine Forderung für die Raum-Zeit-Transformationseigenschaften masseloser Zustände so ganz nebenbei eine Begründung für die Eichbedingungen von Feldern liefert. Mehr zu Eichtheorien siehe Die Grenzen der Berechenbarkeit Kapitel 5.4.4 und folgende. Details zum Zusammenhang zwischen Nulldrehungen und Eichtransformationen kommen später in Kapitel 4.14.
Die Lorentzmatrizen \(\Lambda_u\) für die Wigner-Rotationen in masselosen Fall haben wir oben bereits kennengelernt. Wir wollen nun noch die entsprechende \(SL(2,\mathbb{C})\)-Matrix \(u\) ausrechnen, wobei \(u\) im masselosen Fall nicht unitär zu sein braucht. Dazu verwenden wir die allgemeine Formel \[ g \, \sigma(p) \, g^+ = \sigma(\Lambda p) \] (hier steht \(\sigma\) für die Paulimatrizen) und setzen darin \(\Lambda_u\) für \(\Lambda\), \(k\) für \(p\) und \(u\) für \(g\) ein (vorsicht: \(u\) ist hier nicht unitär!): \[ u \, \sigma(k) \, u^+ = \sigma(\Lambda_u k) \] Da \(\Lambda_u\) eine Wigner-Rotation ist, haben wir darin \(\Lambda_u k = k \). Mit \( k = (1,0,0,1) \) folgt: \[ u \, (1 + \sigma_3) \, u^+ = (1 + \sigma_3) \] Die 2-mal-2-Matrix \( (1 + \sigma_3) \) ist nun eine sehr einfache Matrix: Sie hat nur links oben eine 2 und ansonsten nur Nullen. Für die vier Matrixelemente \(u_{ij}\) der Matrix \(u\) folgt damit: \[ u_{11} \, u_{11}^* = 1 \] \[ u_{11} \, u_{21}^* = 0 \] \[ u_{21} \, u_{11}^* = 0 \] \[ u_{21} u_{21}^* = 0 \] Aus der vierten Gleichung folgt \[ u_{21} = 0 \] Damit sind die zweite und dritte Gleichung automatisch erfüllt. Die erste Gleichung besagt, dass \( |u_{11}| = 1 \) sein muss, d.h. \(u_{11}\) ist eine komplexe Phase. Wir schreiben daher \[ u_{11} = e^{-i \varphi/2} \] (ja, man erahnt schon die Drehmatrix zu \(R(\varphi)\) ). Und schließlich muss \(u\) auch noch aus \(SL(2,\mathbb{C})\) sein, also \( \det{u} = 1 \) erfüllen: \[ u_{11} u_{22} + u_{12} u_{21} = 1 \] Setzten wir hier ein, was wir bereits wissen, so folgt \[ u_{22} = e^{i \varphi/2} \] Das einzige Matrixelement, für das es keine Einschränkungen gibt, ist \(u_{12}\), welches wir als \[ u_{12} = b \, e^{i \varphi/2} \] schreiben wollen mit einer passenden komplexen Zahl \(b\). Unsere Wigner-Rotation \(u\) sieht also bei masselosen Teilchen so aus: \[ u = \begin{pmatrix} e^{-i \varphi/2} & b \, e^{i \varphi/2} \\ 0 & e^{i \varphi/2} \end{pmatrix} \] (siehe z.B. Hendrik van Hees: Introduction to Relativistic Quantum Field Theory, Kapitel B.4.2 mit etwas anderen Vorzeichenkonventionen).
Analog zur Gleichung \[ \Lambda_u = \Lambda_N(\delta,\eta) \, R(\varphi) \] können wir u also auch schreiben als
| \(SL(2,\mathbb{C})\)-Matrix zur Wigner-Rotation bei masselosen Teilchen: \[ u = u_N(\delta,\eta) \, e^{-i \frac{\varphi}{2} \sigma_3} \] mit \[ u_N = \begin{pmatrix} 1 & b \\ 0 & 1 \end{pmatrix} \] |
wobei die komplexen Zahl \(b\) mit den reellen Parametern \(\delta\) und \(\eta\) zusammenhängt. Diesen Zusammenhang können wir leicht ausrechnen, indem wir in \[ g \, \sigma(p) \, g^+ = \sigma(\Lambda p) \] für \(p\) den Vektor \(e_0\) einsetzen, für \(\Lambda\) die Matrix \(\Lambda_N\) und für \(u\) die Matrix \(u_N\): \[ u_N \, \sigma(e_0) \, u_N^+ = \sigma(\Lambda_N e_0) \] Rechts steht der erste Spaltenvektor von \(\Lambda_N\), umgewandelt in die entsprechende hermitesche Matrix (vergleiche ganz oben die explizite Formel für die Matrix \sigma(x) ). Links ist \(\sigma(e_0) = 1\) die Einheitsmatrix. Schreibt man die Matrizen aus, so liest man ab: \[ b = \delta - i \eta \] Das passt gut dazu, dass sich bei Multiplikation von zwei Nulldrehungen die Parameter addieren müssen. Analog addieren sich auch die komplexen Zahlen \(b\) und \(b'\), wenn man zwei Matrizen \(u_N\) und \(u_N'\) multipliziert.
Damit wäre eigentlich alles zum masselosen Fall gesagt. Es ist jedoch nützlich, sich noch einmal einige Gedanken zur Darstellung auf Feldern zu machen, so wie wir sie oben hergeleitet haben. Das Problem bei masselosen Teilchen ist nämlich: Die Helizität \(\sigma\) ändert sich bei Poincarétransformationen nicht, d.h. sie eignet sich nicht als Matrixindex, so wie dies bei Masse größer Null beim Spinindex noch der Fall war. Als Komplikation kommt hinzu, dass Nulldrehungen sich nur auf den Teilchenimpuls, nicht aber über die Phase auswirken. Die oben hergeleiteten Formeln für die Darstellung auf Feldern ergeben also keine besonders nützlichen Ergebnisse, wenn wir die Helizität als Matrixindex verwenden.
Schön wäre es, wenn wir wieder einen Spinindex wie beim Fall mit Masse größer Null einführen könnten. Das macht besonders dann Sinn, wenn wir den masselosen Fall als Grenzfall des massiven Falls mit Grenzübergang Masse gegen Null betrachten wollen. Starten wir also mit den Zustandsvektoren \[ | \boldsymbol{p} s m_s \rangle \] die wir im Fall massiver Teilchen betrachtet haben (siehe oben die Betrachtung der kleinen Gruppe bei Masse größer Null), und versuchen wir, eine Verbindung von den so definierten Spinzuständen \( | \boldsymbol{p} s m_s \rangle \) zu den Helizitätszuständen \[ |\boldsymbol{p},\sigma \rangle \] herzustellen, die wir bei den masselosen Teilchen verwendet haben, wobei \(\sigma\) die Helizität und \(m_s\) die Spinkomponente in z-Richtung ist.
Die Idee ist nun Folgende: Die Helizität wird oft auch als Spinkomponente in Impulsrichtung bezeichnet. Wenn wir also nur Impulse in z-Richtung betrachten, wo müssten Spin und Helizität identisch sein. Die Poincarétransformationen, die den Impuls in z-Richtung belassen, müssten sich dann auf Spinzustände und Helizitätszustände in gleicher Weise auswirken. Diese Poincarétransformationen lassen sich aus Drehungen um die z-Achse und Boosts in z-Richtung zusammensetzen. Bei masseloser Teilchen kommen noch die Nulldrehungen hinzu. Überprüfen wir also, wie sich in diesen Fällen Spinzustände und Helizitätszustände mit Impuls in z-Richtung transformieren. Dazu müssen wir jeweils die zugehörige Wigner-Rotation berechnen. Dabei kommt uns zu Gute, dass die \(SL(2,\mathbb{C})\)-Matrizen \(g\) bei Boosts in z-Richtung und bei Drehungen um die z-Achse jeweils reine Diagonalmatrizen sind – daher vertauschen sie miteinander. Das werden wir ausnutzen.
Drehungen um die z-Achse:
Setzen wir für \(\Lambda\) eine Drehung \(R(\varphi)\) um die z-Achse ein, und entsprechend für \(g\) die zugehörige Matrix \(u(\varphi)\). Die Matrix \(g(p)\) ist ein Boost in z-Richtung, der \(k\) in \(p\) umwandelt (\( \boldsymbol{p} = |\boldsymbol{p}| \boldsymbol{e}_3\) liegt ja in z-Richtung, d.h. \( p = (E, |\boldsymbol{p}| \boldsymbol{e}_3) \) ). Außerdem ist \( \Lambda \, p = R(\varphi) \, p = p \), so dass \( g(\Lambda p) = g(p) \) ist. Sowohl \(g(p)\) als auch \(u(\varphi)\) sind diagonal, vertauschen also miteinander. Damit lautet die Wigner-Rotation: \[ u = \] \[ = g(\Lambda p)^{-1} \, g \, g(p) = \] \[ = g(p)^{-1} \, u(\varphi) \, g(p) = \] \[ = g(p)^{-1} \, g(p) \, u(\varphi) = \] \[ = u(\varphi) \] d.h. die Wigner-Rotation \(u\) ist selbst die Drehung \(u(\varphi)\) um die z-Achse. Diese Drehung wird bei Spinzuständen und bei Helizitätszuständen durch die gleiche Diagonal-Matrix \(D(u(\varphi))\) dargestellt, wenn wir \(\sigma = m_s\) setzen.
Boost in z-Richtung:
Schauen wir uns nun bei Impuls in z-Richtung an, wie die Wigner-Rotation bei einem Boost \(\Lambda = \Lambda_b\) mit zugehörigem \(g = g_b\) in z-Richtung aussieht. Dazu brauchen wir insbesondere \(g(\Lambda_b p)\). Das ist ein Boost in z-Richtung, der aus \(k\) den Vektor \( \Lambda_b p \) macht. Diesen Boost können wir zusammensetzen aus dem Boost \(g(p)\), der aus \(k\) den Impuls \(p\) macht, und dem Boost \(g_b\), der aus \(p\) den Impuls \(\Lambda_b p\) macht. Also ist \( g(\Lambda_b p) = g_b \, g(p)\) und damit \( g(\Lambda_b p)^{-1} = g(p)^{-1} \, g_b^{-1}\). Setzen wir dies ein: \[ u = \] \[ = g(\Lambda_b p)^{-1} \, g_b \, g(p) = \] \[ = g(p)^{-1} \, g_b^{-1} \, g_b \, g(p) = \] \[ = 1 \] Die Wigner-Rotation ist also die Identität und die wird bei Helizitätszuständen und bei Spinzuständen durch \(D(u) = 1\) dargestellt.
Nulldrehungen:
Bei den Drehungen um die z-Achse und den Boosts in z-Richtung spielte es in der obigen Betrachtung keine Rolle, ob wir massive oder masselose Zustände betrachten. Bei den Nulldrehungen ist das anders: Nur bei masselosen Teilchen belassen sie den Impuls \( p = p^0 \, k \) mit \( k = (1, 0, 0, 1) \) in z-Richtung.
Für eine Nulldrehung \( \Lambda = \Lambda_N \) und entsprechend \( g = u_N \) ist \[ \Lambda_N \, p = \] \[ = \Lambda_N \, p^0 \, k = \] \[ = p^0 \, \Lambda_N \, k = \] \[ = p^0 \, k = p \] d.h. der Impuls in z-Richtung ändert sich nicht – vorausgesetzt, die Masse ist Null! Entsprechend ist wie bei den Drehungen \( g(\Lambda_N \, p) = g(p) \), d.h. beide sind derselbe Boost in z-Richtung. Diese Boostmatrix hat die Form (siehe oben) \[ g(p) = \] \[ = 1 \, \cosh{\frac{\alpha}{2}} + \sigma(\boldsymbol{e}_3) \, \sinh{\frac{\alpha}{2}} = \] \[ = 1 \, \cosh{\frac{\alpha}{2}} + \sigma_3 \, \sinh{\frac{\alpha}{2}} = \] \[ = \begin{pmatrix} \cosh{\frac{\alpha}{2}} + \sinh{\frac{\alpha}{2}} & 0 \\ 0 & \cosh{\frac{\alpha}{2}} - \sinh{\frac{\alpha}{2}} \end{pmatrix} = \] \[ = \begin{pmatrix} e^{\alpha/2} & 0 \\ 0 & e^{- \alpha/2} \end{pmatrix} \] Dabei haben wir die Darstellung \( \cosh{x} = (e^x + e^{- x})/2 \) und \( \sinh{x} = (e^x - e^{- x})/2 \) verwendet (siehe Wikipedia: Sinus hyperbolicus und Kosinus hyperbolicus). Damit lautet die Wigner-Rotation: \[ u = \] \[ = g(\Lambda p)^{-1} \, g \, g(p) = \] \[ = g(p)^{-1} \, u_N \, g(p) = \] \[ = \begin{pmatrix} e^{- \alpha/2} & 0 \\ 0 & e^{\alpha/2} \end{pmatrix} \, \begin{pmatrix} 1 & b \\ 0 & 1 \end{pmatrix} \, \begin{pmatrix} e^{\alpha/2} & 0 \\ 0 & e^{- \alpha/2} \end{pmatrix} = \] \[ = \begin{pmatrix} e^{- \alpha/2} & 0 \\ 0 & e^{\alpha/2} \end{pmatrix} \, \begin{pmatrix} e^{\alpha/2} & b \, e^{- \alpha/2} \\ 0 & e^{- \alpha/2} \end{pmatrix} = \] \[ = \begin{pmatrix} 1 & b \, e^{- \alpha} \\ 0 & 1 \end{pmatrix} = \] \[ = \begin{pmatrix} 1 & b' \\ 0 & 1 \end{pmatrix} = \] \[ = u_N' \] d.h. \( u_N' \) eine Nulldrehungsmatrix mit dem Matrixelement \( b' = b \, e^{- \alpha} \) oben rechts. Die Wigner-Rotation einer Nulldrehung ist also bei Impuls in \(k\)-Richtung bei masselosen Teilchen wieder eine Nulldrehung. Die Darstellungsmatrix \(D(u_N')\) ist dann gleich \(1\), denn Nulldrehungen wirken sich nach Definition nicht auf die Helizität aus.
Was macht eine Nulldrehung mit Spinzuständen bei Impuls in z-Richtung? Diese wollen wir ja als Grenzfall massiver Zustände mit Masse gegen Null auffassen. Bei massiven Teilchen ist nun die Wigner-Rotation immer eine Drehmatrix aus \(SU(2)\) – eine Nulldrehung gehört nicht dazu. Wir müssen uns also ansehen: Was geschieht mit der Wigner-Rotation einer Nulldrehung bei massiven Teilchen mit Impuls in z-Richtung, wenn die Masse gegen Null geht? Wiederholen wir also die obige Berechnung der Wigner-Rotation bei massiven Teilchen mit Masse gegen Null. Man kann leicht mit Hilfe der \(\Lambda_N\)-Matrix nachrechnen, dass bei Masse gegen Null der Term \( \Lambda_N p \) gegen \(p\) geht (mit \(p\) in z-Richtung) – so wie in der Analyse für masselose Teilchen. Die Berechnung der Wigner-Rotation geht also genauso wie im masselosen Fall und wir können wieder mit der obigen Formel arbeiten, d.h. \( u = u_N' \) mit \( b' = b \, e^{- \alpha}\). Das wäre allerdings keine \(SU(2)\)-Matrix. Aber bei massiven Teilchen muss die Wigner-Rotation eine \(SU(2)\)-Matrix sein. Was läuft hier schief?
Ganz einfach: Der masselose Grenzfall wirkt sich zusätzlich noch auf die Rapidität \(\alpha\) aus. Es muss nämlich bei massiven Teilchen \[ p = \Lambda_p \, \begin{pmatrix} m \\ \boldsymbol{0} \end{pmatrix} \] sein. Setzt man hier die Boostmatrix von ganz oben ein, so erhält man \[ p = \begin{pmatrix} p^0 \\ |\boldsymbol{p}| \boldsymbol{e}3 \end{pmatrix} = \] \[ = \Lambda_p \, \begin{pmatrix} m \\ \boldsymbol{0} \end{pmatrix} = \] \[ = \begin{pmatrix} (\cosh{\alpha}) & (\sinh{\alpha}) \, \boldsymbol{e}_3 \\ (\sinh{\alpha}) \, \boldsymbol{e}_3 & \mathbb{1} + (\cosh{\alpha} - 1) \, (\boldsymbol{e}_3 \, \boldsymbol{e}_3^T) \end{pmatrix} \, \cdot \] \[ \cdot \, \begin{pmatrix} m \\ \boldsymbol{0} \end{pmatrix} = \] \[ = \begin{pmatrix} m \, \cosh{\alpha} \\ m \, \sinh{\alpha} \, \boldsymbol{e}_3 \end{pmatrix} \] Wenn hier die Masse \(m\) gegen Null geht, so muss die Rapidität \(\alpha\) gegen Unendlich gehen, um ein endliches \(p^0\) und \( |\boldsymbol{p}| \) sicherzustellen.
Das ist auch anschaulich klar: Je leichter ein Teilchen ist, umso größer muss seine Geschwindigkeit sein, um eine vorgegebene Energie \(p^0\) zu erreichen, d.h. umso stärker muss der Boost ausfallen, um vom Ruhesystem aus diese Geschwindigkeit zu erreichen.
Noch ein Hinweis: Die Teilchengeschwindigkeit bleibt natürlich immer kleiner-gleich der Lichtgeschwindigkeit, wobei die Lichtgeschwindigkeit erst bei unendlicher Rapidität erreicht wird. Im Grenzfall masseloser Teilchen können wir also in der obigen Formel für \(u = u_N'\) die Rapidität \( \alpha \) gegen Unendlich gehen lassen. Damit geht \( b' = b \, e^{- \alpha} \) gegen Null und die Wignerrotation \(u\) geht gegen \(1\) (zum Glück – eine \(SU(2)\)-Matrix!).
Die entsprechende Darstellungsmatrix \(D(u_N)\) ist dann bei den Spinzuständen im masselosen Grenzfall ebenfalls \(1\) – wie bei den Helizitätszuständen. Übrigens: Gäbe es kontinuierliche Nulldrehungs-Quantenzahlen, so wäre \(D(u_N)\) bei den Helizitätszustanden nicht einfach \(1\), anders als bei den Spinzuständen. Man kann also masselose Helizitätszustände nur dann als masselosen Grenzfall massiver Teilchenzustände verstehen, wenn es keine kontinuierlichen Nulldrehungs-Quantenzahlen gibt. Offenbar hat sich die Natur dafür entschieden, dass masselose Teilchen von Teilchen mit sehr geringer Masse kaum unterscheidbar sein sollen – eine physikalisch sicher nachvollziehbare Forderung.
Damit habe wir das gewünschte Ergebnis:
Alle Poincarétransformationen, die bei masselosen Teilchen den Impuls in z-Richtung belassen,
wirken sich auf Spinzustände (mit Quantisierungsachse in Impulsrichtung – hier die z-Achse)
und Helizitätszustände gleich aus, wobei wir
masselose Spinzustände als masselosen Grenzfall massiver Spinzustände verstehen.
Wir setzen also
| \[ | \, |\boldsymbol{p}| \boldsymbol{e}_3 , \sigma \rangle = | \, |\boldsymbol{p}| \boldsymbol{e}_3 , s m_s \rangle \] mit \( \sigma = m_s \). |
Welchen Wert wir für den Gesamtspin \(s\) auf der rechten Seite nehmen sollen, ist erst einmal nicht festgelegt (er muss nur größer-gleich \(\sigma\) sein, damit \(\sigma = m_s\) sein kann). Normalerweise aber betrachtet man nicht nur einen, sondern gleich mehrere Helizitätswerte gemeinsam, z.B. 1 und -1 . Dann wird man \(s=1\) wählen. Meist kommt man auch umgekehrt von einer Darstellung mit bestimmtem Gesamtspin \(s\) und betrachtet den masselosen Grenzfall – dann ist \(s\) sowieso vorgegeben.
Wie kommt man nun zu beliebigen Impulsen? Den Impulsbetrag können wir schon in z-Richtung passend wählen. Also brauchen wir nur noch eine Drehung \(R(\boldsymbol{w})\), die den Impuls von der z-Achse in die gewünschte Richtung dreht (die entsprechende \(SU(2)\)-Matrix nennen wir \(u(\boldsymbol{w})\) ). Es ist also \[ \boldsymbol{p} = R(\boldsymbol{w}) \, |\boldsymbol{p}| \, \boldsymbol{e}_3 \] Dabei parametrisiert \(\boldsymbol{w}\) wie gewohnt die Drehachse und den Drehwinkel. Anschaulich ist klar, dass die Drehachse senkrecht auf der gewünschten Impulsrichtung und der z-Achse steht, und dass der Drehwinkel gleich dem Winkel zwischen Impulsrichtung und z-Achse ist. Wenden wir also die Drehung auf die obige Gleichung an: \[ T_{u(\boldsymbol{w})} \, | \, |\boldsymbol{p}| \boldsymbol{e}_3 , \sigma \rangle = \, T_{u(\boldsymbol{w})} \, | \, |\boldsymbol{p}| \boldsymbol{e}_3 , s m_s \rangle \] Bei den Spinzuständen wissen wir von oben, dass für eine Drehung \(u(\boldsymbol{w})\) die Wigner-Rotation \(u\) gerade identisch mit der Drehung \(u(\boldsymbol{w})\) ist: \(u = u(\boldsymbol{w})\). Diese Außage bleibt auch im masselosen Grenzfall gültig (sonst würde es auch keinen Sinn mehr machen, \(m_s\) in diesem Grenzfall als Spinindex zu interpretieren). Also ist auf der rechten Seite \[ T_{u(\boldsymbol{w})} \, | \, |\boldsymbol{p}| \boldsymbol{e}_3 , s m_s \rangle = \sum_{m_s'} \, | \boldsymbol{p} , s m_s' \rangle \, D^s_{m_s' m_s}(u(\boldsymbol{w})) \] Nun zur linken Seite. Als erstes müssen wir die Wigner-Rotation \(u\) für masselose Teilchen bei der Drehung \(R(\boldsymbol{w})\) ausrechnen, wobei der Impuls in z-Richtung \( |\boldsymbol{p}| \boldsymbol{e}_3 \) bzw. der zugehörige Viererimpuls \( p^0 \, k \) verwendet wird.
Wir können die Konvention treffen, dass \(g(p^0 \, k)\) ein Boost in z-Richtung sein soll (d.h. wir schließen Nulldrehungen aus, so wie wir bei massiven Teilchen Drehungen im Ruhesystem für g(p) ausgeschlossen haben). Wie sieht es mit \( g(R(\boldsymbol{w}) \, p^0 \, k) = g(p) \) aus?
Das ist eine Lorentztransformation, die aus \(k\) den Impuls \(p\) macht. Diese können wir zusammensetzen aus dem Boost \(g(p^0 \, k)\) in z-Richtung, der die Energie auf \(p^0\) einstellt, und der anschließenden Drehung \(u(\boldsymbol{w})\), die den Impuls ausrichtet. Also ist \[ g(R(\boldsymbol{w}) \, p^0 \, k) = g(p) = u(\boldsymbol{w}) \, g(p^0k) \] Damit können wir die Wigner-Rotation ausrechnen: \[ u = \] \[ = g(R(\boldsymbol{w}) \, p^0 \, k)^{-1} \, u(\boldsymbol{w}) \, g(p^0k) = \] \[ = g(p^0 \, k)^{-1} \, u(\boldsymbol{w})^{-1} \, u(\boldsymbol{w}) \, g(p^0k) = \] \[ = 1 \] Die Wigner-Rotation ist also die Identität! Das ist auch anschaulich klar, denn die Wigner-Rotation im masselosen Fall muss ja eine Drehung um die z-Achse mit anschließender Nulldrehung sein. Nulldrehungen können wir ignorieren, da sie in \(D(u)\) nicht berücksichtigt werden, und eine Drehung um die z-Achse tritt hier nicht auf, da die Drehachse \(\boldsymbol{w}\) senkrecht zur z-Achse steht.
Wir haben hier also den interessanten Fall, dass die Wigner-Rotation im masselosen Fall nicht identisch ist mit der Wigner-Rotation im massiven Fall mit Masse gegen Null. Die Ursache liegt in dem Term \( g(R(\boldsymbol{w}) \, p^0 \, k) = g(p) \) in der Wigner-Rotation. Das ist die Lorentztransformation, die aus dem Standardimpuls \(k\) den Impuls \( p = R(\boldsymbol{w}) \, p^0 \, k \) macht. Im massiven Fall können wir hierfür einen Boost in \(\boldsymbol{p}\)-Richtung wählen, denn \(\boldsymbol{k} = \boldsymbol{0}\). Im masselosen Fall ist dagegen \(\boldsymbol{k} = \boldsymbol{e}_3\), so dass wir neben dem Boost zusätzlich die Drehung \(u(\boldsymbol{w})\) mit einbauen müssen, die dann den anderen Term \(u(\boldsymbol{w})\) neutralisiert.
Da die Wigner-Rotation im masselosen Fall die Identität ist, haben wir für die linke Seite oben die Gleichung: \[ T_{u(\boldsymbol{w})} \, | \, |\boldsymbol{p}| \boldsymbol{e}_3 , \sigma \rangle = |\boldsymbol{p}, \sigma \rangle \] Insgesamt folgt also aus \[ T_{u(\boldsymbol{w})} \, | \, |\boldsymbol{p}| \boldsymbol{e}_3 , \sigma \rangle = T_{u(\boldsymbol{w})} \, | \, |\boldsymbol{p}| \boldsymbol{e}_3 , s m_s \rangle \] folgender Zusammenhang:
| Zusammenhang zwischen masselosen Helizitätszuständen und Spinzuständen im Grenzfall Masse gegen Null: \[ |\boldsymbol{p}, \sigma \rangle = \sum_{m_s'} \, | \boldsymbol{p} , s m_s' \rangle \, D^s_{m_s' m_s}(u(\boldsymbol{w})) \] mit \( m_s = \sigma \). Dabei gehört die \(SU(2)\)-Matrix \(u(\boldsymbol{w})\) zur Lorentz-Drehmatrix \(R(\boldsymbol{w})\) mit \( \boldsymbol{p} = R(\boldsymbol{w}) \, |\boldsymbol{p}| \, \boldsymbol{e}_3 \), d.h. \( R(\boldsymbol{w}) \) dreht die z-Achse in Impulsrichtung. |
Anschaulich kann man sich vorstellen, dass auf der rechten Seite der Formel der Spin durch die Matrix \(D(u(\boldsymbol{w}))\) von der z-Richtung in die \(\boldsymbol{p}\)-Richtung gedreht wird, so dass seine Projektion auf \(\boldsymbol{p}\) wieder gleich der Helizität \(\sigma\) ist, so wie das zuvor in z-Richtung der Fall war.
Ein Operator, der diese Projektion des Spins auf die Impulsrichtung darstellen sollte, ist der Helizitätsoperator \[ \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} \] Also müsste der Helizitätsoperator, angewendet auf den Helizitätszustand, als Eigenwert diese Helizität haben. Überprüfen wir es (wobei wir immer wieder die Darstellungseigenschaft verwenden, die Darstellungsmatrix des Spinoperators \(\hat{S}_i\) gleich der Darstellungsmatrix des entsprechenden \(SU(2)\)-Generators \(\sigma_i/2\) setzen, \( m_s = \sigma \) verwenden, die Gleichung \[ u(\boldsymbol{w})^{-1} \, \sigma(\boldsymbol{p}) \, u(\boldsymbol{w}) = \] \[ = \sigma(R(\boldsymbol{w})^{-1} \boldsymbol{p}) = \] \[ = \sigma(|\boldsymbol{p}| \, \boldsymbol{e}_3) = \] \[ = |\boldsymbol{p}| \, \sigma_3 \] sowie die Linearität der Darstellung benutzen): \[ \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} \, |\boldsymbol{p}, \sigma \rangle = \] \[ = \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} \, \sum_{m_s'} \, | \boldsymbol{p} , s m_s' \rangle \, \cdot \] \[ \cdot \, D^s_{m_s' m_s}(u(\boldsymbol{w})) = \] \[ = \sum_{m_s' m_s''} \, | \boldsymbol{p} , s m_s'' \rangle \, \langle \boldsymbol{p} , s m_s'' | \, \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|}) \, | \boldsymbol{p} , s m_s' \rangle \, \cdot \] \[ \cdot \, D^s_{m_s' m_s}(u(\boldsymbol{w})) = \] \[ = \sum_{m_s' m_s''} \, | \boldsymbol{p} , s m_s'' \rangle \, D^s_{m_s'' m_s'} \left(\frac{\sigma(\boldsymbol{p})}{2|\boldsymbol{p}|}\right) \, \cdot \] \[ \cdot \, D^s_{m_s' m_s}(u(\boldsymbol{w})) = \] \[ = \sum_{m_s''} \, | \boldsymbol{p} , s m_s'' \rangle \, \cdot \] \[ \cdot \, D^s_{m_s'' m_s} ( \sigma(\boldsymbol{p}) u(\boldsymbol{w}) ) \frac{1}{2|\boldsymbol{p}|} = \] \[ = \sum_{m_s''} \, | \boldsymbol{p} , s m_s'' \rangle \, \cdot \] \[ \cdot \, D^s_{m_s'' m_s} ( u(\boldsymbol{w}) \, u(\boldsymbol{w})^{-1} \, \sigma(\boldsymbol{p}) \, u(\boldsymbol{w}) ) \frac{1}{2|\boldsymbol{p}|} = \] \[ = \sum_{m_s''} \, | \boldsymbol{p} , s m_s'' \rangle \, D^s_{m_s'' m_s} ( u(\boldsymbol{w}) \sigma_3 ) \, \frac{1}{2} = \] \[ = \sum_{m_s' m_s''} \, | \boldsymbol{p} , s m_s'' \rangle \, D^s_{m_s'' m_s'}(u(\boldsymbol{w})) \, D^s_{m_s' m_s}(\hat{S}_3) = \] \[ = \sum_{m_s''} \, | \boldsymbol{p} , s m_s'' \rangle \, D^s_{m_s'' m_s}(u(\boldsymbol{w})) \, m_s = \] \[ = \sigma \, |\boldsymbol{p}, \sigma \rangle \] Nochmal zusammengefasst:
| \[ \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} \, |\boldsymbol{p},\sigma\rangle = \sigma \, |\boldsymbol{p},\sigma\rangle \] |
Nun zu den Impulsamplituden und den Feldern:
Einen allgemeinen masselosen Zustand mit Helizität \(\sigma\)
können wir analog zum Zustand mit Masse schreiben als
\[
|\psi, \sigma \rangle =
\]
\[ =
\int \frac{d^3p}{2 p^0} \, h^{\sigma}(\boldsymbol{p}) \, |\boldsymbol{p},\sigma\rangle
\]
Diese Gleichung definiert die Impulsamplitude in Helizitätsdarstellung
\( h^{\sigma}(\boldsymbol{p}) \), wobei wir den Helizitätsindex hier oben schreiben wollen.
Vorsicht: es gibt hier keine Summe über die Helizität,
denn da diese Poincare-invariant ist, haben wir sie
(wie die Masse Null) als invariante Eigenschaft des Gesamtzustandes \(
|\psi,\sigma\rangle \) gewählt.
Drücken wir nun wieder die Helizitätszustände durch die Spinzustände aus,
so haben wir
\[
|\psi, \sigma \rangle =
\]
\[ =
\sum_{m_s'} \,
\int \frac{d^3p}{2 p^0} \, h^{\sigma}(\boldsymbol{p}) \,
| \boldsymbol{p} , s m_s' \rangle \, \cdot
\]
\[ \cdot \,
D^s_{m_s' \sigma} (u(\boldsymbol{w}))
\]
wobei wir \( \sigma = m_s \)explizit eingesetzt haben.
Dies können wir mit der Definition der Impulsamplituden
in Spindarstellung vergleichen, wobei wir zusätzlich
die Helizität festlegen und diese als Index oben an den Impulsamplituden anbringen
(dazu sagen wir etwas weiter unten noch Genaueres):
\[
|\psi, \sigma\rangle =
\]
\[ =
\sum_{m_s'} \,
\int \frac{d^3p}{2 p^0} \, f^{\sigma}_{s m_s'}(\boldsymbol{p}) \,
| \boldsymbol{p} , s m_s' \rangle
\]
Der Vergleich der beiden Formeln ergibt:
| Zusammenhang zwischen Impulsamplituden in Helizitätsdarstellung und Impulsamplituden in Spindarstellung: \[ h^{\sigma}(\boldsymbol{p}) \, D^s_{m_s' \sigma} (u(\boldsymbol{w})) = f^{\sigma}_{s m_s'}(\boldsymbol{p}) \] Vorsicht: in der Formel steht keine Summe über \(\sigma\), auch wenn der Index doppelt vorkommt. Die Matrix \(D^s_{m_s' \sigma} (u(\boldsymbol{w})) \) ist eine Funktion von \(\boldsymbol{p}\), denn \(u(\boldsymbol{w})\) gehört zu der Drehung \(R(\boldsymbol{w})\), die die z-Richtung in \(\boldsymbol{p}\)-Richtung dreht. |
Natürlich können wir diesen Zusammenhang mit der inversen \(D\)-Matrix auch nach \( h^{\sigma}(\boldsymbol{p}) \) freistellen. Die Bedeutung des hochgestellten \(\sigma\)-Indexes in \( f^{\sigma}_{s m_s'}(\boldsymbol{p}) \) kann man sich noch etwas genauer klarmachen, denn er bedeutet, dass die Impulsamplituden \( f^{\sigma}_{s m_s'}(\boldsymbol{p}) \) Nebenbedingungen erfüllen müssen (sonst würden sie nicht zur Helizität \(\sigma\) gehören). Es gibt nämlich insgesamt \( 2 (s + 1) \) Werte für \(m_s'\), also auch \( 2 (s + 1) \) Impulsamplituden \( f^{\sigma}_{s m_s'}(\boldsymbol{p}) \). Die obige Gleichung sagt aber, dass nur eine von ihnen unabhängig sein kann, denn alle lassen sich aus einer einzigen Funktion \( h^{\sigma}(\boldsymbol{p}) \) berechnen.
Der Helizitätsoperator liefert eine naheliegende Möglichkeit, die Nebenbedingungen für die Impulsamplituden zu formulieren. Dazu definieren wir den Helizitätsoperator wie gewohnt auf den Impulsamplituden: \[ \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} \, |\psi, \sigma \rangle =: \] \[ = \sum_{m_s'} \, \int \frac{d^3p}{2 p^0} \, \left[ \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} f(\boldsymbol{p}) \right]^{\sigma}_{s m_s'} \, | \boldsymbol{p} , s m_s' \rangle \] Wegen \[ \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} \, |\psi, \sigma\rangle = \sigma \, |\psi, \sigma \rangle \] gilt dann \[ \left[ \frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|} f(\boldsymbol{p}) \right]^{\sigma}_{s m_s'} = \sigma \, f^{\sigma}_{s m_s'}(\boldsymbol{p}) \] Andererseits ist \[ \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} \, |\psi, \sigma\rangle = \] \[ = \sum_{m_s'} \, \int \frac{d^3p}{2 p^0} \, f^{\sigma}_{s m_s'}(\boldsymbol{p}) \, \frac{\boldsymbol{\hat{S} \hat{P}}}{|\hat{\boldsymbol{P}}|} \, | \boldsymbol{p} , s m_s' \rangle = \] \[ = \sum_{m_s' m_s} \, \int \frac{d^3p}{2 p^0} \, f^{\sigma}_{s m_s'}(\boldsymbol{p}) \, | \boldsymbol{p} , s m_s \rangle \, D^s_{m_s m_s'}(\frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|}) = \] \[ = \sum_{m_s m_s'} \, \int \frac{d^3p}{2 p^0} \, D^s_{m_s' m_s}(\frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|}) \, f^{\sigma}_{s m_s}(\boldsymbol{p}) \, | \boldsymbol{p} , s m_s' \rangle \] so dass Vergleich mit oben ergibt: \[ \left[ \frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|} f \right]^{\sigma}_{s m_s'}(\boldsymbol{p}) = \] \[ = D^s_{m_s' m_s}\left(\frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|}\right) \, f^{\sigma}_{s m_s}(\boldsymbol{p}) \] Weglassen der Spin-Indices ergibt damit in Matrixschreibweise die Bedingung:
| Helizitätsbedingung für die Impulsamplituden in Spindarstellung: \[ \left[ \frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|} f \right]^{\sigma}_s(\boldsymbol{p}) = \] \[ = D^s \left(\frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|} \right) \, f^{\sigma}_s(\boldsymbol{p}) = \] \[ = \sigma \, f^{\sigma}_s(\boldsymbol{p}) \] d.h. der Spinor der Impulsamplituden ist Eigenvektor der Matrix \( D^s \left(\frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|} \right) \) zur Helizität \(\sigma\) als Eigenwert. Dabei bedeutet die Schreibweise \( D^s \left(\frac{\boldsymbol{\hat{S} p}}{|\boldsymbol{p}|} \right) \), dass die Darstellungsmatrizen der drei Spinoperatoren gebildet werden, dann die Linearkombination dieser Matrizen mit den drei Impulskomponenten gebildet wird und zum Schluss noch durch den Impulsbetrag dividiert wird. |
Nun zu den Feldern. Diese hatten wir aus den Impulsamplituden über die Gleichung \[ F(p) := D(g(p)) \, f(\boldsymbol{p}) \] (mit \( p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \) ) definiert. Diese Definition gilt bei Masse größer Null. Wir müssen nun den Grenzübergang Masse gegen Null durchführen. Das kann allerdings problematisch werden, denn \(g(p)\) ist ein Boost des Ruheimpulses \( (m, \boldsymbol{0}) \) zum Impuls \(p\), und oben hatten wir bereits gesehen, dass bei Masse gegen Null die Rapidität dieses Boosts gegen Unendlich geht, um dasselbe \(p\) trotz verschwindender Masse noch erreichen zu können. Es ist also unklar, ob sich masselose Felder überhaupt so einfach definieren lassen.
Schauen wir uns dazu einige Details an. Oben hatten wir festgestellt, dass die Impulsamplitude zur Helizität \(\sigma\) allgemein die Form \[ h^{\sigma}(\boldsymbol{p}) \, D^s_{m_s' \sigma} (u(\boldsymbol{w})) = f^{\sigma}_{s m_s'}(\boldsymbol{p}) \] hat. Die Äbhängigkeit der Impulsamplitude vom Spinindex ist also durch die Drehmatrix \(D^s\) vollkommen festgelegt. Sie entspricht der Spalte mit Nummer \(\sigma\) in dieser Drehmatrix. Für die Felder haben wir dann (wir schreiben die Indices und alle Summen hier aus) \[ F^{\sigma}_{s m_s}(p) := \] \[ := \sum_{m_s'} \, D^s_{m_s m_s'}(g(p)) \, f^{\sigma}_{s m_s'}(\boldsymbol{p}) = \] \[ = \sum_{m_s'} \, D^s_{m_s m_s'}(g(p)) \, h^{\sigma}(\boldsymbol{p}) \, D^s_{m_s' \sigma} (u(\boldsymbol{w})) \] Analog zu den Drehmatrizen haben wir dabei auch bei den Boosts die Schreibweise \(D^s(g(p)) \) verwendet, also oben einen Spinindex \(s\) hinzugefügt. Genau genommen ist das bisher nur für Drehungen definiert. Wir wollen das hier so verstehen: Wir verwenden eine Darstellung \(D(g)\) für ganz \(SL(2,\mathbb{C})\), die für Drehungen \(g = u\) die üblichen Drehmatrizen \(D^s(u)\) ergibt. Ob damit die Darstellungsmatrix auch für Boosts eindeutig festliegt, werden wir unten noch sehen. Es wird sich herausstellen, dass sie nicht eindeutig festliegt.
Die obige Formel bedeutet: Um den Feld-Spaltenvektor \( F^{\sigma}_s(p) \) zu bilden, wird das Matrixprodukt \(D^s(g(p)) \, D^s(u(\boldsymbol{w})) \) gebildet, dann die Spalte Nummer \(\sigma\) davon genommen und mit der skalaren Funktion \( h^{\sigma}(\boldsymbol{p}) \) multipliziert.
Wegen der Darstellungseigenschaft ist \[ D^s(g(p)) \, D^s(u(\boldsymbol{w})) = D^s(g(p) u(\boldsymbol{w})) \] Bei der Untersuchung der kleinen Gruppe massiver Teilchen hatten wir oben außerdem die Formel \[ u(\boldsymbol{w}) \, g(p) = g(Rp) \, u(\boldsymbol{w}) \] abgeleitet. Sie besagt: Man kann erst in \(p\)-Richtung boosten und dann drehen, oder erst drehen und dann in die gedrehte Richtung \(Rp\) boosten. In dieser Formel können wir \(Rp =: p'\) bzw. \(p = R^{-1}p'\) setzen und den Strich wieder weglassen, d.h. \[ u(\boldsymbol{w}) \, g(R^{-1}p) = g(p) \, u(\boldsymbol{w}) \] Das können wir nun in der Darstellungsmatrix verwenden: \[ D^s(g(p) \, u(\boldsymbol{w})) = D^s(u(\boldsymbol{w}) \, g(R^{-1}p)) \] Nun ist aber rechts \( R^{-1} p = p^0 \, (1,\boldsymbol{e}_3) \). Wir haben also:
| Zusammenhang zwischen einem Feld und der Impulsamplitude in Helizitätsdarstellung: \[ F^{\sigma}_{s m_s}(p) = \sum_{m_s'} \, h^{\sigma}(\boldsymbol{p}) \, \cdot \] \[ \cdot \, D^s_{m_s m_s'}(u(\boldsymbol{w})) \, D^s_{m_s' \sigma} (g(p^0 (1,\boldsymbol{e}_3))) \] |
Es wird also ein Boost in z-Richtung ausgeführt, um die Energie \(p^0\) zu erreichen, und die Spalte Nummer \(\sigma\) der entsprechenden Darstellungsmatrix gebildet. Dieser Spaltenvektor wird mit der skalaren Funktion \(h^{\sigma}(\boldsymbol{p})\) multipliziert und mit der Drehmatrix \(D^s(u(\boldsymbol{w}))\) gedreht. Für Masse gegen Null geht dabei die Rapidität des Boosts in z-Richtung gegen unendlich, was zu Divergenzen führen kann. Wir können versuchen, diese Divergenzen durch einen Normierungsfaktor \(N_m\) aufzufangen, den wir formal von der Masse \(m\) abhängig wählen können und der im masselosen Grenzfall geeignet gegen Null gehen muss, so dass der folgende Ausdruck konvergiert:
| \[ H^{\sigma}_{s m_s}(p) := N_m \, F^{\sigma}_{s m_s}(p) = \] \[ = N_m \, \sum_{m_s'} \, h^{\sigma}(\boldsymbol{p}) \, \cdot \] \[ \cdot \, D^s_{m_s m_s'}(u(\boldsymbol{w})) \, D^s_{m_s' \sigma} (g(p^0 (1,\boldsymbol{e}_3))) \] |
Der Normierungsfaktor \(N_m\) hat ja weiter keine Auswirkungen auf die Transformationseigenschaften des Feldes, so dass diese Vorgehensweise legitim ist. Mehr dazu in den nächsten Kapiteln am Beispiel von Spin 0, 1/2 und 1.
Wir hatten oben bereits die Darstellung der Poincarégruppe auf Feldern im Ortsraum und im Impulsraum kennengelernt. Im Ortsraum hatten wir beispielsweise \[ [T_{g,a} \psi](x) = D(g) \, \psi(\Lambda^{-1}(x - a)) \] hergeleitet. Dabei war \( D(g) \) eine endlich-dimensionale komplexe Darstellungsmatrix der Lorentzgruppe bzw. genauer deren Überlagerungsgruppe \(SL(2,\mathbb{C})\). Für zwei Elemente \(g\) und \(g'\) aus \(SL(2,\mathbb{C})\) soll also \( D(g g') = D(g) \, D(g') \) sein. Endlich-dimensional sollte sie sein, um etwas mit einer Einteilchen-Darstellung zu tun zu haben, bei der der Index \(\sigma\) nur endlich viele diskrete Werte annehmen kann. Die Aspekte unendlich-dimensionaler Darstellungen kommen über die Abhängigkeit der Funktion \(\psi\) vom kontinuierlichen Vierervektor \(x\) ins Spiel (beispielsweise kann man \(\psi\) nach einem vollständigen Funktionensystem entwickeln, das aus unendlich vielen Basisfunktionen besteht).
Da die Lorentzgruppe wegen der Boosts nicht kompakt ist, sind alle unitären Darstellungen unendlich-dimensional (bis auf die triviale Darstellung). Oben hatten wir diese Darstellungen bereits kennengelernt. Da \( D(g) \) aber eine endlich-dimensionale Darstellungsmatrix sein soll, kann sie nicht (immer) unitär sein. Das unterscheidet \( D(g) \) von den Darstellungsmatrizen \( D(u) \), die unitär gewählt werden können. Für die \(SL(2,\mathbb{C})\)-Untergruppe \(SU(2)\) kann man natürlich für \( D(g) \) die Drehmatrizen \( D(u) \) nehmen. Bei den Boosts geht das nicht – hier sehen die Matrizen \( D(g) \) anders aus!
Um die möglichen Matrizen \( D(g) \) zu ermitteln, kann man wie bei der Drehgruppe über die Darstellungen der Lie-Algebra gehen. Dazu haben wir oben bereits alles Wichtige kennengelernt. Sammeln wir es noch einmal:
Insbesondere sind die drei Generatoren \(A(J_i)\) der Drehungen hermitesch, die drei Generatoren \(A(K_i)\) der Boosts dagegen antihermitesch. Das gilt auch für die Generatoren der Gruppe \(SL(2,\mathbb{C})\), die wir direkt anhand der obigen Formeln für \(u\) und \(e^h\) ablesen können:
Natürlich erfüllen auch die Matrizen \(\sigma_k / 2 \) und \(- i \sigma_k / 2 \) die obige Lie-Algebra, denn \(SL(2,\mathbb{C})\) hat ja als Überlagerungsgruppe der Lorentzgruppe dieselbe Lie-Algebra wie diese. Der Faktor \( - i \) führt dabei zu dem negativen Vorzeichen im Kommutator der Boost-Generatoren.
Eine allgemeine Lorentztransformation kann man nun schreiben als \[ \Lambda = e^{i \boldsymbol{\alpha} A(\boldsymbol{K}) - i \boldsymbol{w} A(\boldsymbol{J})} \] Grund: die Exponentialabbildung ist für die Lorentzgruppe surjektiv (siehe Lie Groups, Lie Algebras and the Exponential Map). Vorsicht: das ist nicht dasselbe wie \( e^{i \boldsymbol{\alpha} A(\boldsymbol{K})} \, e^{- i \boldsymbol{w} A(\boldsymbol{J})} \), da die Generatoren für Boosts und Drehungen nicht vertauschen.
Im Exponenten steht ein allgemeines Element der Lie-Algebra: \[ i \boldsymbol{\alpha} A(\boldsymbol{K}) - i \boldsymbol{w} A(\boldsymbol{J}) \] (das \(i\) führen wir hier mit). Dabei umfassen die Vektoren \(\boldsymbol{\alpha}\) und \(\boldsymbol{w}\) insgesamt 6 reelle Parameter. Es ist nun nützlich, neue Generatoren \(J^{(1)}_k\) und \(J^{(2)}_k\) einzuführen (der Grund für diese Bezeichnungsweise wird gleich noch sichtbar): \[ J_k^{(1)} := \frac{1}{2} \, ( A(J_k) + i A(K_k) ) \] \[ J_k^{(2)} := \frac{1}{2} \, ( A(J_k) - i A(K_k) ) \] Vorsicht: da hier ein \(i\) vorkommt, sind dies keine Elemente der reellen Lie-Algebra der Lorentzgruppe mehr, die ja nur Linearkombinationen der Generatoren mit reellen Koeffizienten zulässt. Das macht aber nichts: Bei der Drehgruppe hatten wir in Kapitel 4.8 auch Leiteroperatoren \(J^+\) und \(J^-\) außerhalb der reellen Lie-Algebra gebildet. Die Umkehrung der obigen Formeln lautet nun: \[ A(J_k) = \; \; J_k^{(1)} + J_k^{(2)} \] \[ A(K_k) = - i \, (J_k^{(1)} - J_k^{(2)}) \] Damit können wir das Element der Lie-Algebra im Exponenten umschreiben: \[ i \boldsymbol{\alpha} A(\boldsymbol{K}) - i \boldsymbol{w} A(\boldsymbol{J}) = \] \[ = i \boldsymbol{\alpha} (- i) (\boldsymbol{J}^{(1)} - \boldsymbol{J}^{(2)}) + \] \[ - i \boldsymbol{w} (\boldsymbol{J}^{(1)} + \boldsymbol{J}^{(2)}) = \] \[ = (\boldsymbol{\alpha} - i \boldsymbol{w}) \boldsymbol{J}^{(1)} - (\boldsymbol{\alpha} + i \boldsymbol{w}) \boldsymbol{J}^{(2)} \] Rechnen wir die Kommutatoren der neuen Generatoren aus. Dazu schreiben wir etwas kürzer \(J_i\) statt \(A(J_i)\) usw., d.h. wir haben \[ - [K_i, K_j] = [J_i, J_j] = i \epsilon_{ijk} J_k \] \[ [J_i, K_j] = - [K_j, J_i] = \] \[ = - [J_j, K_i] = [K_i, J_j] = i \epsilon_{ijk} K_k \] Damit ist \[ [J_i^{(1)}, J_j^{(1)}] = \] \[ = [J_i + i K_i , J_j + i K_j] / 4 = \] \[ = ( [J_i, J_j] + i [J_i, K_j] + \] \[ + i [K_i, J_j] - [K_i, K_j] ) / 4 = \] \[ = ( 2 i \epsilon_{ijk} J_k + 2 i i \epsilon_{ijk} K_k ) / 4 = \] \[ = i \epsilon_{ijk} ( J_k + i K_k ) / 2 = \] \[ = i \epsilon_{ijk} J_k^{(1)} \] Die Rechnung für \( [J_i^{(2)}, J_j^{(2)}] \) geht genauso, nur dass wir überall \( K \) durch \( -K \) (mit entsprechendem Index) ersetzen müssen. Das Ergebnis lautet \[ [J_i^{(2)}, J_j^{(2)}] = i \epsilon_{ijk} J_k^{(2)} \] Bei der Rechnung für \( [J_i^{(1)}, J_j^{(2)}] \) müssen wir im Vergleich zu \( [J_i^{(1)}, J_j^{(1)}] \) überall \( K_j \) durch \( - K_j \) ersetzen (nur für den Index \(j\), nicht für den Index \(i\)). Der erste und vierte sowie der zweite und dritte Term löschen sich dann aus, anstatt sich zu addieren, so dass \[ [J_i^{(1)}, J_j^{(2)}] = 0 \] ist, d.h. die \(J^{(1)}\) 's und \(J^{(2)}\) 's vertauschen miteinander. Fassen wir zusammen:
|
Umgeschriebene Lie-Algebra der Lorentzgruppe: Die neuen Generatoren \[ J_k^{(1)} := \frac{1}{2} \, ( A(J_k) + i A(K_k) ) \] \[ J_k^{(2)} := \frac{1}{2} \, ( A(J_k) - i A(K_k) ) \] erfüllen die Vertauschungsrelationen \[ [J_i^{(1)}, J_j^{(1)}] = i \epsilon_{ijk} J_k^{(1)} \] \[ [J_i^{(2)}, J_j^{(2)}] = i \epsilon_{ijk} J_k^{(2)} \] \[ [J_i^{(1)}, J_j^{(2)}] = 0 \] d.h. die \(J^{(1)}\) 's und \(J^{(2)}\) 's erfüllen getrennt für sich jeweils die Lie-Algebra der Drehgruppe (bzw. ihrer Überlagerungsgruppe \(SU(2)\) ). Sie verhalten sich also wie zwei Drehimpulsoperatoren, die getrennt voneinander in einem entsprechenden Tensorprodukt-Raum operieren (siehe Kapitel 4.8). Darin lag der Sinn, die neuen Generatoren einzuführen.
|
Die endlich-dimensionalen Darstellungen der Überlagerungsgruppe \(SL(2,\mathbb{C})\) können nun aus den endlich-dimensionale Darstellungen der Lie-Algebra über die Exponentialreihe gebildet werden (bis auf eine Feinheit, auf die wir gleich zurückkommen). Wir suchen also die endlich-dimensionalen Darstellungen dieser Lie-Algebra, d.h. wir suchen Matrizen \( D(J_i^{(1)}) \) und \( D(J_i^{(2)}) \), die die obigen Vertauschungsrelationen erfüllen.
Wie das geht, wissen wir aus Kapitel 4.8, wo wir die Darstellung der Drehgruppe auf Tensorprodukten untersucht haben. Dort haben wir zwei Drehimpulsoperatoren \(\boldsymbol{J}^{(1)}\) und \(\boldsymbol{J}^{(2)}\) betrachtet, die beide für sich getrennt die Drehimpulsalgebra erfüllen und die miteinander vertauschen. Ein Beispiel dafür waren der Bahndrehimpuls und der Spin. Analog wählen wir auch hier einen komplexen Darstellungs-Vektorraum mit Basisvektoren \[ | j m \rangle \otimes | j' m' \rangle = | j m, j' m' \rangle \] so dass wir die gesuchten Matrizen wie folgt wählen können: \[ D^{j,j'}_{nn',mm'}(J_i^{(1)}) = \] \[ = \langle j n, j' n' | J_i^{(1)} | j m, j' m' \rangle = \] \[ = \langle j n | J_i^{(1)} | j m \rangle \, \langle j' n' | j' m' \rangle = \] \[ = D^j_{nm}(J_i) \, \delta_{n'm'} \] \[ \] \[ D^{j,j'}_{nn',mm'}(J_i^{(2)}) = \] \[ = \langle j n, j' n' | J_i^{(2)} | j m, j' m' \rangle = \] \[ = \langle j n | j m \rangle \, \langle j' n' | J_i^{(2)} | j' m' \rangle = \] \[ = D^{j'}_{n'm'}(J_i) \, \delta_{nm} \] Dabei sind \(D^j(J_i)\) und \(D^{j'}(J_i)\) die Drehimpulsmatrizen zum Drehimpuls \(j\) und \(j'\), die wir aus Kapitel 4.8 kennen (ich habe den Hut über dem \(J\) nicht immer hingeschrieben). Die Indexpaare \(nn'\) und \(mm'\) kann man als Doppelindex ansehen. Der gesamte Darstellungsraum ist also (2j+1) mal (2j'+1) - dimensional.
Mit diesen konkreten Ausdrücken für die Matrizen können wir nun sofort konkrete Ausdrücke für die Darstellungsmatrizen der Boost- und Drehgeneratoren ableiten: \[ D^{j,j'}(J_k) = \; \; \; D^{j,j'}(J_k^{(1)}) + D^{j,j'}(J_k^{(2)}) \] \[ D^{j,j'}(K_k) = - i \, ( D^{j,j'}(J_k^{(1)}) - D^{j,j'}(J_k^{(2)}) ) \] Die obere Zeile entspricht formal der Addition zweier Drehimpulsoperatoren zu einem Gesamt-Drehimpulsoperator. Die obigen Matrizen kann man nun verwenden, um mit Hilfe der Exponentialreihe die Darstellungsmatrizen \(D(g)\) für Lorentztransformationen zu gewinnen, beispielsweise für Boosts oder Drehungen. Man kann die Darstellungsmatrizen \(D(g)\) auch in einen Zusammenhang mit den Darstellungsmatrizen \(D^j(u)\) für Drehungen bringen, und zwar so:
Die Darstellung der Lorentztransformationen \[ \Lambda = \] \[ = e^{i \boldsymbol{\alpha} A(\boldsymbol{K}) - i \boldsymbol{w} A(\boldsymbol{J})} = \] \[ = e^{(\boldsymbol{\alpha} - i \boldsymbol{w}) \boldsymbol{J}^{(1)} - (\boldsymbol{\alpha} + i \boldsymbol{w}) \boldsymbol{J}^{(2)}} \] (siehe oben) überträgt sich auf die Darstellungsmatrizen \(D(g)\), die wir nun als \( D^{j,j'}(g) \) bezeichnen wollen:
| \[ D^{j,j'}(g) := \] \[ = e^{i \boldsymbol{\alpha} D^{j,j'}(\boldsymbol{K}) - i \boldsymbol{w} D^{j,j'}(\boldsymbol{J})} = \] \[ = e^{(\boldsymbol{\alpha} - i \boldsymbol{w}) D^{j,j'}(\boldsymbol{J}^{(1)}) - (\boldsymbol{\alpha} + i \boldsymbol{w}) D^{j,j'}(\boldsymbol{J}^{(2)})} = \] \[ = D^j( i(\boldsymbol{\alpha} - i \boldsymbol{w})) \otimes D^{j'}( -i(\boldsymbol{\alpha} + i \boldsymbol{w})) \] |
mit den Drehmatrizen \(D^j\) und \(D^{j'}\) aus Kapitel 4.8 sowie der Schreibweise \[ [D^j \otimes D^{j'}]_{nn',mm'} = D^j_{nm} \, D^{j'}_{n'm'} \] ganz analog zur Tensorprodukt-Darstellung von Drehungen. Es gibt allerdings einen Unterschied: Die Drehmatrizen \(D^j\) und \(D^{j'}\) hängen jetzt nicht mehr von reellen Zahlen (den Drehwinkeln) ab, sondern von komplexen Zahlen (\boldsymbol{\alpha} und \boldsymbol{w} sind reell)! Das ergibt sich ganz zwanglos oben aus den Exponentialreihen, die eine entsprechende analytische Fortsetzung der Drehmatrizen definieren. Man kann nun wie bei den Drehungen einen Basiswechsel mit Hilfe der Clebsch-Gordan-Koeffizienten durchführen und so die Matrix \( D^{j,j'}(g) \) in Blockform bringen (also die endlich-dimensionale Darstellung ausreduzieren).
Die Drehimpulsmatrizen sind hermitesch – zumindest kann man die Basis immer so wählen, dass sie es sind, denn jede Darstellung von \(SU(2)\) kann durch Basiswechsel unitär gemacht werden. Entsprechend sind die Darstellungsmatrizen der Lorentz-Drehgeneratoren nach den obigen Formeln auch hermitesch, während die Darstellungsmatrizen der Lorentz-Boostgeneratoren antihermitesch sind. Dies zeigt, dass \(D^{j,j'}(g)\) im Allgemeinen keine unitäre Matrix ist (sie ist nur bei Drehungen unitär, aber nicht bei Boosts). Darin spiegelt sich wieder, dass es bei nicht-kompakten Gruppen wie der Lorentzgruppe keine endlich-dimensionalen unitären Darstellungen gibt. Es ist nicht schlimm, dass \(D^{j,j'}(g)\) nicht unitär ist, denn wir betrachten hier ja Darstellungen auf Feldern und nicht auf Zustandsvektoren im Hilbertraum.
Schauen wir uns konkret die Darstellung mit \(j = \frac{1}{2}\) und \(j' = 0\) an. Hier können wir die gestrichenen Indices weglassen und direkt schreiben \[ D^{\frac{1}{2}, 0}(g) = \] \[ = D^{\frac{1}{2}}( i(\boldsymbol{\alpha} - i \boldsymbol{w})) = \] \[ = e^{- i \sigma( i(\boldsymbol{\alpha} - i \boldsymbol{w})) / 2} = \] \[ = e^{\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} \] Für \( \boldsymbol{\alpha} = 0 \) haben wir also die Drehmatrix \(u\) von oben, und für \(\boldsymbol{w} = 0\) die Boostmatrix \(e^h\) von oben. Wir wollen daher diese Formel als die Standard-Parametrisierung für ein Element \(g\) aus \(SL(2,\mathbb{C})\) ansehen und schreiben \[ g = D^{\frac{1}{2}}( i(\boldsymbol{\alpha} - i \boldsymbol{w})) = \] \[ = e^{\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} \] (genauer legt dies die Abhängigkeit von \(g\) von den Parametern \(\boldsymbol{\alpha}\) und \(\boldsymbol{w}\) fest).
Analog schauen wir uns die Darstellung mit \(j = 0\) und \(j' = \frac{1}{2}\) an. Hier können wir die ungestrichenen Indices weglassen und direkt schreiben \[ D^{0, \frac{1}{2}}(g) = \] \[ = D^{\frac{1}{2}}( -i(\boldsymbol{\alpha} + i \boldsymbol{w})) = \] \[ = e^{- i \sigma( -i(\boldsymbol{\alpha} + i \boldsymbol{w})) / 2} = \] \[ = e^{-\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} = \] \[ = \left( \left( e^{\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w}))} \right)^+ \right)^{-1} = \] \[ = (g^+ )^{-1} \] Die beiden Darstellungen
| \[ D^{\frac{1}{2}, 0}(g) = g \] \[ D^{0, \frac{1}{2}}(g) = (g^+ )^{-1} \] |
kann man nicht durch Basiswechsel ineinander umrechnen. Durch mehrfache Tensorproduktbildung dieser Matrizen und anschließende Ausreduktion kann man alle anderen Darstellungsmatrizen erzeugen (so wie man bei der Drehgruppe mit mehreren Spin 1/2 jeden anderen Drehimpuls aufbauen kann). Man bezeichnet sie deshalb als Fundamentaldarstellungen.
Noch eine interessante Anmerkung am Rande: Wir haben oben \[ g = e^{\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} \] geschrieben. Tatsächlich ist es aber so, dass nicht jede Matrix \(g\) aus \(SL(2,\mathbb{C})\) so geschrieben werden kann! Die Exponentialabbildung von der Lie-Algebra von \(SL(2,\mathbb{C})\) nach \(SL(2,\mathbb{C})\) ist nicht surjektiv. Anders bei der Lorentzgruppe: dort ist die Exponentialabbildung surjektiv (siehe oben). Hier ist eine Matrix aus \(SL(2,\mathbb{C})\), die man nicht als Exponentialreihe schreiben kann: \[ - u_N = - \begin{pmatrix} 1 & b \\ 0 & 1 \end{pmatrix} \] Die dazu negative Matrix \(u_N\) kann man dagegen als Exponentialreihe schreiben. Wir kennen diese Matrix von oben: es handelt sich um die Nulldrehungen. Allgemein ist es bei der Gruppe \(SL(2,\mathbb{C})\) so, dass man immer entweder \(g\) oder \(-g\) (oder beide) als Exponentialreihe schreiben kann. Da beide zur selben Lorentzmatrix gehören, ist verständlich, dass sich eine Lorentzmatrix immer als Exponentialreihe schreiben lässt. Mehr dazu siehe Lie Groups, Lie Algebras and the Exponential Map (speziell Seite 435) sowie Henrik van Hees: Introduction to Relativistic Quantum Field Theory, Appendix B.
Ist es für die obige Analyse nun schlimm, dass sich nicht jede Matrix \(g\) als Exponentialreihe schreiben lässt? Vermutlich nicht: Die Nulldrehungen sind eigentlich nur bei masselosen Teilchen interessant, und für diese Teilchen haben wir festgelegt, dass sie auf den physikalischen Zuständen trivial durch den Eins-Operator dargestellt werden. Außerdem kann man jede Matrix \(g\) als Produkt einer hermiteschen und einer unitären Matrix schreiben, und da sich diese jeweils als Exponentialreihe schreiben lassen, kann man jedes Element aus \(SL(2,\mathbb{C})\) zumindest als Produkt zweier Exponentialreihen von Matrizen aus der Lie-Algebra schreiben. Notfalls hat man demnach eben ein Produkt der entsprechenden Darstellungsmatrizen. Anders ausgedrückt: Hat man eine Matrix \(g\), die sich nicht als Exponentialreihe schreiben lässt, so kann man mit einer 360-Grad-Drehung daraus die Matrix \(-g\) machen, und die lässt sich dann als Exponentialreihe schreiben.
Hört sich alles plausibel an, aber wer weiß: Diese Begründungen sind doch typische handwaving arguments, und der Teufel steckt oft im Detail. Es würde aber zu weit führen, hier in eine detaillierte Analyse einzusteigen.
Damit sind wir am Ende dieses recht umfangreichen Kapitels angekommen. Natürlich gäbe es noch sehr viel mehr über die Poincarégruppe, ihre Überlagerungsgruppe und deren Darstellungen zu sagen. Einige Beispiele für offene Fragen:
Wir werden diese Fragen nicht allgemein beantworten, sondern uns in den nächsten Kapiteln die wichtigsten Beispiele dazu ansehen. Außerdem wollen wir uns noch einmal mit der Frage beschäftigen, wie man auf die Gruppe \(SL(2,\mathbb{C})\) als Überlagerungsgruppe der Lorentzgruppe kommt.
© Jörg Resag, www.joerg-resag.de
last modified on 17 August 2023