Die beiden Massenschalen. Die Nullkomponente \(p^{0}\) ist nach oben und \(\boldsymbol{p}\) horizontal aufgetragen. Credit: Lars H. Rohwedder (gemeinfrei), Quelle: Wikipedia File:Hyperboloid2.png ):
Nach dem Ausflug zu Clifford-Algebren und Spingruppen im letzten Kapitel wollen wir in diesem Kapitel wieder an das vorletzte Kapitel 4.10 anknüpfen. Dabei wollen wir am Beispiel der skalaren Felder genauer auf die Bedeutung dieser Felder und ihre Verbindung zu den quantenmechanischen Zuständen eingehen.
Fassen wir noch einmal zusammen, was wir über Quantenzustände und Felder in Kapitel 4.10 erfahren haben (Details siehe dort). Zu den Einteilchen-Zuständen und ihren Transformationseigenschaften hatten wir gelernt:
|
Quantenmechanische Einteilchen-Zustände und ihre Transformation:
Ein quantenmechanischer Einteilchen-Zustand
\( | \boldsymbol{p}, \sigma \rangle \)
mit Impuls \(\boldsymbol{p}\)
transformiert sich bei einer Poincarétransformation nach den Formeln
\[
T_g \, |\boldsymbol{p},\sigma\rangle
=
\]
\[ =
\sum_{\sigma'} \, | \Lambda \boldsymbol{p}, \sigma' \rangle
D_{\sigma'\sigma}(u)
\]
Bei massiven Teilchen kann man \(\sigma\) kann als Spinkomponente interpretieren und für \(D(u)\) eine Drehmatrix im Ruhesystem des Teilchens wählen. Bei masselosen Teilchen kann man dagegen \(\sigma\) als Helizität interpretieren, wobei \(D(u)\) diagonal in \(\sigma\) ist. \(T_g\) und \(T_{h(a)}\) verändern das Skalarprodukt \[ \langle\boldsymbol{p}',\sigma' | \boldsymbol{p},\sigma \rangle = 2p^{0} \, \delta^{3}(\boldsymbol{p}' - \boldsymbol{p}) \, \delta_{\sigma,\sigma'} \] der Zustände nicht, sind also eine unitäre Darstellung.
|
Von den Zuständen haben wir uns nun schrittweise zu den Feldern
vorgearbeitet. Dazu haben wir zunächst die Impulsamplitude
\( f_{\sigma}(\boldsymbol{p}) \) eingeführt:
\[
|\psi\rangle =
\sum_{\sigma} \,
\int \frac{d^{3}p}{2p^{0}} \, f_{\sigma}(\boldsymbol{p}) \, |\boldsymbol{p},\sigma\rangle
\]
Eine Transformation \(T_g\) dieses Zustandes \( |\psi\rangle \)
können wir nun als Transformation der Impulsamplitude darstellen:
\[
[T_g f](\boldsymbol{p})
=
D(u') \,
f(\Lambda^{-1}\boldsymbol{p})
\]
mit der Impuls-abhängigen Wigner-Rotation
\[
u' = g(p)^{-1} \, g \, g(\Lambda^{-1}p)
\]
und der unitären Matrix \(D(u')\) (die auf den hier unterdrückten Index \(\sigma\) wirkt).
Ein einfacheres Transformationsverhalten ergibt sich, wenn wir von den Impulsamplituden f(\boldsymbol{p}) zu den Feldern \(F(p)\) übergehen (dabei ist in \(F(p)\) die Null-Komponente von \(p\) durch \[ p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}} \] festgelegt): \[ F(p) := D(g(p)) \, f(\boldsymbol{p}) \] \[ [T_g F](p) := D(g(p)) \, [T_g f](\boldsymbol{p}) \] denn dann lautet das Transformationsverhalten \[ [T_g F](p) = D(g) \, F(\Lambda^{- 1}p) \] Die Darstellungsmatrix \(D(g)\) muss dabei für allgemeine \(g\) aus \(SL(2,\mathbb{C})\) nicht unitär sein. Das hat Folgen, wenn wir das Skalarprodukt mit Hilfe der Felder ausdrücken: \[ \langle\psi'|\psi\rangle = \] \[ = \int \frac{d^{3}p}{2p^{0}} \, [f '(\boldsymbol{p})]^{+} \, f(\boldsymbol{p}) = \] \[ = \int \frac{d^{3}p}{2p^{0}} \, F'(p)^{+} \, [D(g(p))^{- 1}]^{+} \, \cdot \] \[ \cdot \, D(g(p))^{- 1 } F(p) \] Wir können also \[ \frac{|f_{\sigma}(\boldsymbol{p})|^{2}}{2p^{0}} = \frac{|(D(g(p))^{- 1 } F(p))_{\sigma}|^{2}}{2p^{0}} \] als Impuls-Wahrscheinlichkeits-Dichte interpretieren. Für eine nicht-unitäre Matrix \( D(g(p))^{- 1} \) fällt das Matrixprodukt im Skalarprodukt nicht weg und das Skalarprodukt hat eine recht komplizierte Gestalt, wenn man es durch die Felder \(F(p)\) ausdrückt. Für \(F(p)\) gilt also ein einfaches Transformationsgesetz bei Poincarétransformationen, aber es geht auf komplizierte Weise in das Skalarprodukt ein und hat deshalb auch keine direkte Wahrscheinlichkeits-Interpretation.
Von den Impuls-abhängigen Feldern können wir durch Fouriertransformation zu Raumzeit-abhängigen Feldern übergehen (wobei im oberen Integral \(F(p)\) formal auch für beliebige \(p^{0}\) definiert sein muss, was aber wegen der Delta- und Theta-Funktion keine Rolle spielt): \[ \psi(x) := \] \[ = N \, \int d^{4}p \, F(p) \, e^{- i p x} \, \cdot \] \[ \cdot \, \delta(p^{2} - m^{2}) \, \Theta(p^{0}) = \] \[ = N \, \int \frac{d^{3}p}{2p^{0}} \, F(p^{0},\boldsymbol{p}) \, e^{- i p^{0} t} \, e^{i \boldsymbol{p x}} \] mit \( p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}} \) in der unteren Zeile, der Normierung \( N = (2\pi)^{-3/2} \) und der Minkowski-Metrik \( p x = g(p,x) \).
Wichtig ist, dass bei der Fouriertransformation wegen der Delta-Funktion nur Impulse zur gleichen Masse \(m\) überlagert werden, und wegen der Theta-Funktion \(p^{0} \ge 0 \) erzwungen wird. Für die Transformationseigenschaft bei Poincarétransformationen (inclusive Translationen) ergibt sich die einfache Formel \[ [T_{g,a} \psi](x) = D(g) \, \psi(\Lambda^{-1}(x - a)) \] Wir haben in Kapitel 4.10 bereits gesehen, dass man die Raum-Zeit-Felder \( \psi(x) \) nicht als Wahrscheinlichkeitsamplitude für den Ort (zu vorgegebener Zeit) interpretieren kann. Eine solche Wahrscheinlichkeitsamplitude kann man zwar aus den Impulsamplituden durch Fouriertransformation definieren, aber sie hat kein einfaches Transformationsverhalten unter Poincarétransformationen und sie hängt mit den Feldern \( \psi(x) \) über ein kompliziertes Faltungsintegral zusammen (Details siehe Kapitel 4.10). Aus diesem Faltungsintegral folgt, dass man die Felder \( \psi(x) \) nur als eine Art verschmierte Wahrscheinlichkeitsamplitude für den Ort interpretieren kann.
Nachdem der allgemeine Rahmen nun wieder klar ist, wollen wir uns die skalaren Felder genauer ansehen. Dabei schreiben wir wie üblich für die skalaren Felder hier \(\phi(p)\) statt \(F(p)\).
Wenn \(p^{0}\) darin durch \[ p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}} \] festgelegt ist, schreiben wir \[ \phi_{+}(\boldsymbol{p}) \] Die Funktion \( \phi(p) \) ist also analog zu \(F(p)\) einfach irgendeine stetig-differenzierbare Funktion, die für \( p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}} \) gleich \( \phi_{+}(\boldsymbol{p}) \) ist.
Weiterhin schreiben wir wie üblich \(\phi_{+}(x)\) statt \(\psi(x)\).
Die \(D\)-Matrizen sind hier gleich \(1\), denn es
gibt bei skalaren Feldern keinen \(\sigma\)-Index (oder nur einen
einzigen trivialen, den man auch weglassen kann). Das genau ist ja die Definition eines skalaren Feldes.
Da \(\sigma\) mit dem Spin zusammenhängt, folgt daraus,
dass wir es hier mit spinlosen Teilchen zu tun haben.
Die obigen Formeln für skalare Teilchen und Felder vereinfachen sich also zu:
\[
T_g \, |\boldsymbol{p}\rangle
=
|\Lambda\boldsymbol{p}\rangle
\]
\[
T_{h(a)} |\boldsymbol{p}\rangle =
e^{i g(a,p)} \, |\boldsymbol{p}\rangle
\]
\[
|\phi_{+}\rangle =
\int \frac{d^{3}p}{2p^{0}} \, f(\boldsymbol{p}) \, |\boldsymbol{p}\rangle
\]
\[
[T_g f](\boldsymbol{p})
=
f(\Lambda^{- 1}\boldsymbol{p})
\]
\[
\phi_{+}(\boldsymbol{p}) := f(\boldsymbol{p})
\]
\[
\langle\phi_{+}'|\phi_{+}\rangle =
\int \frac{d^{3}p}{2p^{0}} \, [\phi_{+}'(\boldsymbol{p})]^{+}
\,
\phi_{+}(\boldsymbol{p})
\]
\[
\phi_{+}(x) :=
\]
\[
= N \, \int d^{4}p \, \phi(p) \, e^{- i p x}
\, \delta(p^{2} - m^{2}) \, \Theta(p^{0})
=
\]
\[
= N \, \int \frac{d^{3}p}{2p^{0}} \, \phi_{+}(\boldsymbol{p})
\, e^{- i p^{0} t} \, e^{i \boldsymbol{p x}}
\]
\[
[T_{g,a} \phi_{+}](x)
= \phi_{+}(\Lambda^{- 1}(x - a))
\]
Oben sind wir von einem Quantenzustand ausgegangen und dann schrittweise zu Feldern vorgedrungen. Oft geht man aber auch den umgekehrten Weg und startet mit den Feldern, also in diesem Fall mit skalaren Funktionen \( \phi(x) \), die auf der Raumzeit definiert sind (wir unterscheiden in der Schreibweise nicht zwischen \(\phi(x)\) und der Fouriertransformierten \(\phi(p)\), da das Argument \(x\) oder \(p\) klar macht, um was es sich handelt). Das macht beispielsweise Sinn, wenn man eine klassische Feldtheorie als Ausgangspunkt vorliegen hat und von dieser zu einer Quantentheorie übergehen möchte. Die folgende Darstellung orientiert sich dabei an Schütte: Poincaréskript, 1992 (ITKP, Uni Bonn) sowie an Steven Weinberg: The Quantum Theory of Fields, Vol. 1.
Starten wir also mit einer skalaren stetig-differenzierbaren Funktion (einem Feld) \( \phi(x) \) und versuchen wir, bis zu den Quantenzuständen zu gelangen. Dazu definieren wir zunächst analog zu oben eine Darstellung der Poincarégruppe auf dem Feld: \[ [T_{g,a} \phi](x) := \phi(\Lambda^{- 1}(x - a)) \] Oben hatten wir diese Formel noch herleiten können, da wir wussten, wie sich Quantenzustände transformieren. Hier dagegen gehen wir von einem Feld aus, das noch keine Verbindung zu Quantenzuständen hat. Um diese Verbindung später knüpfen zu können, macht es daher sicher Sinn, die Darstellung der Poincarégruppe auf den Feldern passend zu oben zu definieren.
Nun gibt es natürlich sehr viele skalare Funktionen \(\phi\). Die obige Darstellung verknüpft aber bestimmte skalare Funktionen miteinander, denn \(T_{g,a}\) ist ein Operator, der aus einer skalaren Funktion eine andere skalare Funktion macht. Der Raum der skalaren Funktionen zerfällt dadurch in Unterräume von skalaren Funktionen, wobei sich die Funktionen in einem Unterraum durch die Menge aller \(T_{g,a}\) ineinander transformieren lassen. Dieses Zerlegen in solche Unterräume haben wir auch als Ausreduktion der Darstellung kennengelernt. Die Darstellung bewegt sich immer nur innerhalb eines Unterraums.
Wir wollen nun versuchen, diese Unterräume durch eine bestimmte Gleichung zu charakterisieren, wobei diese Gleichung einen Parameter enthält, der den Unterraum kennzeichnet. Die Gleichung dient also zur Ausreduktion der Darstellung. Analog war es bei den Drehungen, bei denen der Gesamtdrehimpuls ein solcher kennzeichnender Parameter ist.
Welcher Parameter könnte in einer solchen Gleichung eine Rolle spielen? Wenn wir oben den Weg von den Zuständen zu den Feldern betrachten, so sehen wir, dass zwei Parameter in Frage kommen: Die Masse (also das Quadrat des Viererimpulses) und der Gesamtspin. Da der Spin hier Null ist, bleibt noch die Masse \(m\) übrig. Das wird besonders deutlich in der Formel \[ \phi_{+}(x) := \] \[ = N \,\int d^{4}p \, \phi(p) \, e^{- i p x} \, \delta(p^{2} - m^{2}) \, \Theta(p^{0}) \] von oben, über die wir \(\phi_{+}(x)\) definiert hatten mit der Folge, dass alle diese \(\phi_{+}(x)\) einen ausreduzierten Darstellungsraum der Poincarégruppe bilden, denn auch alle über \[ [T_{g,a} \phi_{+}](x) := \phi_{+}(\Lambda^{- 1}(x - a)) \] definierten Felder lassen sich wie \(\phi_{+}(x)\) als ein solches Fourierintegral mit demselben \(m\) darstellen.
Versuchen wir also, eine Gleichung mit einem Parameter \(m\) für unsere Felder \(\phi(x)\) zu finden, so dass sich die Lösungen dieser Gleichung zu diesem \(m\) über \(T_{g,a}\) ineinander transformieren. Vermutlich müssen sich die Lösungen dann ähnlich dem obigen Fourierintegral schreiben lassen, denn dieses garantiert ja gerade diese Eigenschaft.
Aus Kapitel 4.7 wissen wir: Auf ortsabhängigen Funktionen wird der Impulsoperator durch \[ -i \frac{d}{d\boldsymbol{x}} \] und der Energieoperator durch \[ i \frac{d}{dt} \] dargestellt (in natürlichen Einheiten). Das garantiert, dass beide Operatoren die Generatoren der Raum-Zeit-Translationen bilden, so wie sie auf den Funktionen \(\phi(x)\) oben dargestellt werden. Das unterschiedliche Vorzeichen kommt übrigens daher, dass wir bei der Fouriertransformation Energie und Impuls mit unterschiedlichem Vorzeichen in der Exponentialfunktion verwenden, so dass sich dort insgesamt die relativistische Minkowski-Metrik ergibt. Nur so ergibt sich die angestrebte physikalische Interpretation von Energie und Impuls.
Fassen wir wie in Kapitel 4.10 beide Operatoren zum Vierer-Impuls-Operator \[ \hat{P} = \hat{P}^{\mu} = ( \hat{H}, \hat{\boldsymbol{P}}) \] zusammen. Dann wollen wir die folgende Bedingung an \(\phi(x)\) stellen:
|
Klein-Gordon-Gleichung: \[ \hat{P}^{2} \phi(x) = m^{2} \, \phi(x) \] Dabei ist \(m\) ein positiver reeller Parameter (den wir später als Masse interpretieren werden) und \[ \hat{P}^{2} = \hat{P}^{\mu} \hat{P}_{\mu} = \] \[ = \left(i \frac{d}{dt}\right)^{2} - \left(-i \frac{d}{d\boldsymbol{x}}\right)^{2} = \] \[ = \left(\frac{d}{d\boldsymbol{x}}\right)^{2} - \left(\frac{d}{dt}\right)^{2} = \] \[ - \frac{d}{dx^{\mu}} \frac{d}{dx_{\mu}} \] |
Leistet diese Gleichung das, was wir erreichen wollen?
Zunächst einmal können wir nachrechnen: Wenn eine Funktion \(\phi(x)\) Lösung dieser Gleichung zu \(m\) ist, so ist auch jede Funktion \( [T_{g,a} \phi](x) := \phi(\Lambda^{- 1}(x - a)) \) Lösung dieser Gleichung zum selben \(m\) (die Rechnung überspringen wir hier).
Der Darstellungs-Operator \( T_{g,a} \) verbindet also Funktionen in einem Lösungsraum der Klein-Gordon-Gleichung zu gegebenem \(m\) miteinander. Es ist aber noch nicht garantiert, dass es nicht in einem Lösungsraum noch kleinere Unterräume gibt, in denen sich \( T_{g,a} \) bewegt. Wir wissen also noch nicht sicher, ob die Lösungsräume auch irreduzible Darstellungsräume der Poincarégruppe sind.
Versuchen wir, die Frage durch Fouriertransformation zu klären. Der Schreibweise in Schütte: Poincaréskript, 1992 (ITKP, Uni Bonn) (Kapitel 5) folgend schreiben wir für die Fouriertransformation: \[ \phi(x) = N \, \int d^{4}p \, h(p) \, e^{- i p x} \] mit \(p x = g(p,x) = p^{\mu} x_{\mu} \) und der fouriertransformierten Funktion \(h(p)\). Vorsicht: noch ist \(p^{0}\) unabhängig von \(\boldsymbol{p}\). Das ändert sich, wenn wir fordern, dass \(\phi(x)\) eine Lösung der Klein-Gordon-Gleichung zu gegebenem \(m\) sein soll: \[ 0 = (\hat{P}^{2} - m^{2}) \, \phi(x) = \] \[ = \left(- \frac{d}{dx^{\mu}} \frac{d}{dx_{\mu}} - m^{2}\right) \] \[ N \, \int d^{4}p \, h(p) \, e^{- i p x} = \] \[ = N \, \int d^{4}p \, h(p) \, \cdot \] \[ \left(- \frac{d}{dx^{\mu}} \frac{d}{dx_{\mu}} - m^{2}\right) \, e^{- i p x} = \] \[ = N \, \int d^{4}p \, h(p) \, (p^{2} - m^{2}) \, e^{- i p x} \] Die Lösung lautet (Details siehe Schütte: Poincaréskript, 1992 (ITKP, Uni Bonn) (Kapitel 5) ): \[ h(p) = \phi(p) \, \delta(p^{2} - m^{2}) \] denn eingesetzt in das Integral ergibt das \[ N \, \int d^{4}p \, \phi(p) \delta(p^{2} - m^{2}) \, \cdot \] \[ \cdot \, (p^{2} - m^{2}) \, e^{- i p x} = \] \[ = N \, \phi(p) \, (p^{2} - m^{2}) \, e^{- i p x} |_{p^{2} = m^{2}} = 0 \] wie verlangt. Halten wir fest:
|
Lösungen der Klein-Gordon-Gleichung: Die Lösungen der Klein-Gordon-Gleichung haben die Form \[ \phi(x) = N \, \int d^{4}p \, \phi(p) \, \cdot \] \[ \cdot \, \delta(p^{2} - m^{2}) \,e^{- i p x} \] |
Das ist schon fast unser Fourierintegral von oben, allerdings fehlt noch die Beschränkung
auf positive \(p^{0}\) durch den Term \(\Theta(p^{0})\).
Im Integral wird also hier über die positive und die negative Massenschale integriert,
nicht nur über die positive.
Wir teilen das Integral daher in die beiden Teilintegrale auf, indem wir den Faktor
\( 1 = \Theta(p^{0}) + \Theta(-p^{0}) \) einfügen
und etwas umsortieren:
\[
\phi(x) =
\]
\[
=
N \, \int d^{4}p \, \phi(p) \, e^{- i p x} \, \cdot
\]
\[ \cdot \,
\, \delta(p^{2} - m^{2}) \, \Theta(p^{0})
+
\]
\[
+
N \, \int d^{4}p \, \phi(p) \, e^{- i p x} \, \cdot
\]
\[ \cdot \,
\, \delta(p^{2} - m^{2}) \, \Theta(-p^{0})
\]
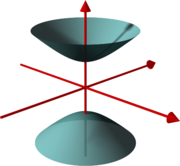
Das erste Integral umfasst Viererimpulse auf der positiven Massenschale (also \(p^{2} = m^{2}\)
und \(p^{0} \ge 0\)), das zweite Integral umfasst Viererimpulse auf der negativen Massenschale
(also wieder \(p^{2} = m^{2}\),
aber diesmal \(p^{0} < 0\)).

Die beiden Massenschalen.
Die Nullkomponente \(p^{0}\) ist nach oben und \(\boldsymbol{p}\) horizontal aufgetragen.
Credit: Lars H. Rohwedder (gemeinfrei), Quelle:
Wikipedia File:Hyperboloid2.png ):
Wie man das erste vierdimensionale Integral in ein dreidimensionales Integral über den Impuls umwandelt, das wissen wir aus Kapitel 4.10. Analog geht es auch bei dem zweiten Integral. Die Rechnung findet man beispielsweise in Schütte: Poincaréskript, 1992 (ITKP, Uni Bonn) (Seite 21). Ergebnis: \[ \phi(x) = \] \[ = N \, \int \frac{d^{3}p}{|2p^{0}|} \, \phi(p) \, e^{- i p x} \bigg|_{ p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}}} + \] \[ + N \, \int \frac{d^{3}p}{|2p^{0}|} \, \phi(p) \, e^{- i p x} \bigg|_{ p^{0} = -\sqrt{m^{2} + \boldsymbol{p}^{2}}} = \] \[ = N \, \int \frac{d^{3}p}{|2p^{0}|} \, \phi_{+}(\boldsymbol{p}) \, e^{- i p x} \bigg|_{ p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}}} + \] \[ + N \, \int \frac{d^{3}p}{|2p^{0}|} \, \phi_{-}(\boldsymbol{p}) \, e^{- i p x} \bigg|_{ p^{0} = -\sqrt{m^{2} + \boldsymbol{p}^{2}}} \] mit \[ \phi_{+}(\boldsymbol{p}) := \phi(p) |_{ p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}}} \] \[ \; \phi_{-}(\boldsymbol{p}) := \phi(p) |_{ p^{0} = -\sqrt{m^{2} + \boldsymbol{p}^{2}}} \] Das erste Integral ist damit genau unser Fourierintegral für Felder, wie wir es aus den Quantenzuständen über die Impulsamplituden oben hergeleitet hatten. Die Klein-Gordon-Gleichung reproduziert also dieses Integral wie gewünscht. Wir wollen es als den Anteil mit positiven Energien bezeichnen.
Aber es gibt ein Problem: Die Lösungen der Klein-Gordon-Gleichung enthalten auch das zweite Integral, das wir als Anteil mit negativen Energien bezeichnen wollen. Diese negativen Energien haben wir für Einteilchenzustände in Kapitel 4.10 als unphysikalisch bezeichnet, denn dann könnte aus dem Nichts heraus ein Teilchen mit positiver Energie und ein Teilchen mit gleich großer negativer Energie und entgegengesetztem räumlichen Impuls entstehen, ohne dass die Energie-Impuls-Erhaltung verletzt wäre. Das Vakuum wäre instabil, denn es könnte ständig solche Teilchenpaare erzeugen. Wir können also die negativen Energien nicht unmittelbar mit der Energie von Einteilchenzuständen identifizieren. Wie sich dieses Problem negativer Energien lösen lässt, sehen wir uns weiter unten an.
Besonders in der etwas älteren Literatur zur Klein-Gordon-Gleichung wird noch ein zweites Problem angesprochen. Man versucht, in Analogie zur Schrödingergleichung aus \(\phi(x)\) eine Orts-Wahrscheinlichkeitsdichte und einen dazugehörigen erhaltenen Vierer-Strom zu konstruieren (siehe z.B. Wikipedia: Klein-Gordon-Gleichung und ausführlich in Schütte: Poincaréskript, 1992 (ITKP, Uni Bonn), Kapitel 4). Das Ergebnis lautet:
|
Vierer-Stromdichte für die Klein-Gordon-Gleichung: \[ j_{\mu}(x) = i \, [ \phi^{*}(x) \, (\delta_{\mu}\phi(x)) - (\delta_{\mu}\phi^{*}(x)) \, \phi(x) ] \]
|
mit \[ \delta_{\mu} := \frac{d}{dx^{\mu}} \] Wenn \(\phi(x)\) die Klein-Gordon-Gleichung erfüllt, so folgt die Stromerhaltung \[ \delta_{\mu} j^{\mu}(x) = 0 \] Und aus \[ [T_{g,a} \phi](x) := \phi(\Lambda^{- 1}(x - a)) \] folgt für den Strom die Gleichung \[ [T_{g,a} j](x) = \Lambda j(\Lambda^{- 1}(x - a)) \] wobei \( [T_{g,a} j] \) dadurch definiert ist, dass statt \(\phi\) darin \([T_{g,a} \phi]\) verwendet wird. \(\Lambda\) ist die Lorentzmatrix, die zu \(g\) gehört. Diese Gleichung besagt nichts anderes, als dass \(j(x)\) ein Vierer-Strom ist.
Aus der Stromerhaltung und der Vierer-Strom-Eigenschaft folgt (siehe wieder Schütte), dass das Integral \[ \int_{t=0} d^{3}x \, j^{ 0}(t,\boldsymbol{x}) = \] \[ = \int_{t=0} d^{3}x \, i \, [ \phi^{*}(x) \, (\delta^{0}\phi(x)) - (\delta^{0}\phi^{*}(x)) \, \phi(x) ] \] poincaréinvariant ist, d.h. \[ \int_{t=0} d^{3}x \, j^{ 0}(t,\boldsymbol{x}) = \int_{t=0} d^{3}x \, [T_{g,a} j]^{ 0}(t,\boldsymbol{x}) \] Wenn man aber nun versucht, in Analogie dazu ein poincaré-invariantes Skalarprodukt über \[ \langle\phi'|\phi\rangle := \] \[ = \int_{t=0} d^{3}x \, i [ \phi'^{*}(x) \, (\delta^{0}\phi(x)) - (\delta^{0}\phi'^{*}(x)) \, \phi(x) ] \] einzuführen, so ist dieses Skalarprodukt zwar bilinear und poincare-invariant, aber wegen dem negativen Vorzeichen nicht positiv definit. Auch \( j^{ 0}(x) \) selbst kann negative Werte annehmen, so dass man es (anders als in der nichtrelativistischen Quantenmechanik) nicht als Wahrscheinlichkeitsdichte interpretieren kann, sondern bestenfalls als Ladungsdichte. Das hat man in der Anfangszeit der Quantentheorie als Problem angesehen, aber wir wissen ja bereits, dass die Felder nicht direkt mit einer Aufenthaltswahrscheinlichkeit zusammenhängen, und dass in der relativistischen Quantentheorie der Begriff der Aufenthaltswahrscheinlichkeit generell problematisch ist (siehe die vorhergehenden Kapitel).
Wie aber sieht es mit dem Skalarprodukt aus? Das braucht man unbedingt, um es als Wahrscheinlichkeitsamplitude zu interpretieren. Im Gegensatz zu den Aussagen in manchen (vor allem älteren) Texten kann man sehr wohl ein positiv definites Skalarprodukt definieren! Dazu schauen wir uns zunächst noch einmal das obige nicht-positiv-definite Skalarprodukt an und drücken es durch die Fourierkomponenten aus. Eine kleine Rechnung ergibt (siehe Schütte): \[ \langle\phi'|\phi\rangle = \] \[ = \int \frac{d^{3}p}{|2p^{0}|} \, [\phi_{+}'(\boldsymbol{p})]^{+} \, \phi_{+}(\boldsymbol{p}) + \] \[ - \int \frac{d^{3}p}{|2p^{0}|} \, [\phi_{-}'(\boldsymbol{p})]^{+} \, \phi_{-}(\boldsymbol{p}) \] Es hindert uns aber formal niemand daran, das Skalarprodukt so zu definieren, dass der Term negativer Energie addiert statt subtrahiert wird. Dadurch entsteht ein positiv definites poincare-invariantes Skalarprodukt: \[ \langle\phi'|\phi\rangle := \] \[ = \int \frac{d^{3}p}{|2p^{0}|} \, [\phi_{+}'(\boldsymbol{p})]^{+} \, \phi_{+}(\boldsymbol{p}) + \] \[ + \int \frac{d^{3}p}{|2p^{0}|} \,[\phi_{-}'(\boldsymbol{p})]^{+} \, \phi_{-}(\boldsymbol{p}) \] Die Poincaré-Invarianz folgt daraus, dass eine Lorentztransformation positive und negative Energien (bei Masse größer-gleich Null) nicht mischt, so dass die Poincaré-Invarianz für jedes Teilintegral separat gilt (Zeitspiegelungen schließen wir dabei aus). Das erste Integral mit den positiven Energien ist genau unser Skalarprodukt, wie wir es oben aus den Einteilchen-Zuständen hergeleitet haben.
Das Problem mit dem Skalarprodukt lässt sich also lösen. Bleibt das Problem mit den negativen Energien, die sich nicht als Teilchenenergien interpretieren lassen. Wie lässt sich eine Verbindung zwischen dem Feld \( \phi(x) \) und Einteilchen-Quantenzuständen knüpfen, so dass bei den Quantenzuständen nur positive Teilchenenergien vorkommen?
Zunächst einmal können wir positive und negative Energien getrennt betrachten: Lorentztransformationen mischen sie nicht, und im Skalarprodukt treten sie auch getrennt voneinander auf. Entsprechend teilen wir \phi(x) folgendermaßen auf:
| \[ \phi(x) = \phi_{+}(x) + \phi_{-}(x) \] mit \[ \phi_{+}(x) = \] \[ = N \, \int \frac{d^{3}p}{|2p^{0}|} \, \phi_{+}(\boldsymbol{p}) \, e^{- i p x} |_{ p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}}} \] \[ \phi_{-}(x) = \] \[ = N \, \int \frac{d^{3}p}{|2p^{0}|} \, \phi_{-}(\boldsymbol{p}) \, e^{- i p x} |_{ p^{0} = -\sqrt{m^{2} + \boldsymbol{p}^{2}}} \] |
Für die beiden Komponenten gilt: \[ [T_{g,a} \phi_{+}](x) = \phi_{+}(\Lambda^{- 1}(x - a)) \] \[ [T_{g,a} \phi_{-}](x) = \phi_{-}(\Lambda^{- 1}(x - a)) \] Der Lösungsraum der Klein-Gordon-Gleichung zu gegebenem \(m\) ist also noch kein irreduzibler Darstellungsraum der Poincarégruppe, denn er lässt sich in zwei irreduzible Teilräume aufteilen: den mit positiver und den mit negativer Energie.
Die Komponente \(\phi_{+}(x)\) haben wir nicht zufällig so genannt, denn sie hat genau die Form, wie wir sie ganz oben aus den Quantenzuständen abgeleitet haben. Diese Komponente \(\phi_{+}(x)\) können wir daher wie oben dazu verwenden, um Einteilchenzustände zu superponieren: \[ |\phi_{+}\rangle = \int \frac{d^{3}p}{2p^{0}} \, \phi_{+}(\boldsymbol{p}) \, |\boldsymbol{p}\rangle \] Bei den negativen Energien wollen wir genau dieselbe Form der Gleichungen erreichen. Dazu setzen wir \[ k := - p \] für alle 4 Komponenten, so dass \(k^{0}\) positiv ist und mit einer Teilchenenergie identifiziert werden kann. Eingesetzt im Integral für \(\phi_{-}(x)\) ergibt das: \[ \phi_{-}(x) = \] \[ = N \, \int \frac{d^{3}k}{2k^{0}} \, \phi_{-}(-\boldsymbol{k}) \, e^{i k x} |_{ k^{0} = \sqrt{m^{2} + \boldsymbol{k}^{2}}} \] Nun müssen wir nur noch komplex konjugieren, um dieselbe Form wie bei den positiven Energien zu erhalten: \[ [\phi_{-}(x)]^{*} = \] \[ = N \, \int \frac{d^{3}k}{2k^{0}} \, [\phi_{-}(-\boldsymbol{k})]^{*} \, e^{- i k x} |_{ k^{0} = \sqrt{m^{2} + \boldsymbol{k}^{2}}} \] In Analogie zu den positiven Energien können wir also einen Quantenzustand hier schreiben als \[ |\phi_{-}\rangle = \int \frac{d^{3}k}{2k^{0}} \, [\phi_{-}(-\boldsymbol{k})]^{*} \, |\boldsymbol{k}\rangle \] Es ist also sehr wohl möglich, Wellenpakete aus den negativen Energie-Anteilen von Klein-Gordon-Feldern zu bilden und diese zu entsprechenden Quantenzuständen zu überlagern. Dabei entspricht die Teilchenenergie dem Betrag der negativen Energie der Klein-Gordon-Lösung, und \( [\phi_{-}(-\boldsymbol{k})]^{*} \) spielt die Rolle der Impulsamplitude \( f(\boldsymbol{k}) \) (siehe oben).
Was das Ganze mit Antiteilchen zu tun hat, das ist momentan allerdings noch nicht zu sehen. Um diesen Zusammenhang herauszuarbeiten müsste man sich mit ladungsartigen Quantenzahlen befassen. Solche Quantenzahlen zeichnen sich dadurch aus, dass für sie bei Wechselwirkungen ein Erhaltungssatz gilt. Man muss sich also Gedanken über die Wechselwirkung von Teilchen machen. Das kann man bei der elektrischen Ladung beispielsweise tun, indem man elektromagnetische Potentiale in die Klein-Gordon-Gleichung einbaut.
Wir wollen hier nicht näher darauf eingehen. Schauen wir uns statt dessen im nächsten Kapitel an, wie der Fall mit Spin 1/2 genauer aussieht. Dabei werden wir auf die Diracgleichung stoßen, die an die Stelle der Klein-Gordon-Gleichung tritt. Außerdem werden wir die Clifford-Algebren aus Kapitel 4.11 benötigen. Mal sehen, ob und wie alle diese Zutaten ein sinnvolles Zusammenspiel ergeben werden.
© Jörg Resag, www.joerg-resag.de
last modified on 22 August 2023