
Das Thema Symmetrien in der Quantentheorie habe ich auch auf meinen anderen Webseiten immer wieder zumindest kurz angerissen:
Um die Beschreibung von Symmetrien in der Quantentheorie wirklich verstehen zu können, muss man sich aber in aller Ruhe die Details ansehen. Auf diese Details möchte ich in diesem und den nächsten Kapiteln genauer eingehen. Dabei möchte ich möglichst präzise die theoretischen Grundlagen darstellen.
Damit das Thema nicht ausufert, werde ich keine expliziten Berechnungen zeigen. Wo immer möglich, werde ich aber sagen, wo man diese Berechnungen finden kann. Eine sehr gute Quelle für solche Details ist Steven Weinbergs Standardwerk The Quantum Theory of Fields, speziell Vol. 1.
Im Physikstudium lernt man in der Vorlesung über Quantenmechanik irgendwann die Drehimpuls-Operatoren kennen. Man befasst sich sogar mit der Drehimpulsalgebra und stößt dabei auf die Möglichkeit, dass es auch halbzahlige Drehimpulse geben kann (sogenannte Fermionen). Vielleicht lernt man sogar, wie sich Wellenfunktionen bei Drehungen transformieren. Im Grunde betreibt man damit schon genau das, worum es in den nächsten Kapiteln gehen soll: Darstellungstheorie von Gruppen.
Aus Zeitgründen kann man aber das Thema aber im Studium meist nicht vertiefen. Wer kennt schon Begriffe wie Überlagerungsgruppe oder Strahldarstellung, und wer hat sich nicht bisweilen die Frage gestellt, was einen Spinor eigentlich von einem Vektor unterscheidet. Vielleicht gelingt es mir hier, diese Fragen zu beantworten.
Erinnern wir uns, was in der Physik eine Symmetrie ist (siehe Kapitel 2.3): Bei einer Symmetrietransformation wechselt man von einer Beschreibung eines physikalischen Vorgangs zu einer anderen, dazu gleichwertigen Beschreibung des Vorgangs. So kann man ein Experiment auch aus einem gleichförmig fahrenden Zug betrachten und in den Koordinaten dieses Zuges beschreiben. Alternativ kann man das Experiment auch auf den Zug montieren und das fahrende Experiment vom Bahnhof aus betrachten (Stichwort: Boost). In den vorhergehenden Kapiteln haben wir uns das am Beispiel der Mechanik genauer angesehen.
Auch in der Quantentheorie geht das. Ein konkretes Beispiel: Betrachten wir ein quantenmechanisches System, das wir durch den Zustandsvektor \( | \psi \rangle \) darstellen können, und betrachten wir einen Satz von Messwerten, wie sie durch einen Zustandsvektor \( | \phi \rangle \) angegeben werden. Dann wissen wir aus dem letzten Kapitel: die Wahrscheinlichkeit, diesen Satz von Messwerten zu finden, ist durch das betragsquadrierte Skalarprodukt \[ | \langle \phi | \psi \rangle |^2 \] gegeben. Das Skalarprodukt hatten wir als Wahrscheinlichkeitsamplitude bezeichnet.
Wenn wir nun das quantenmechanische System in einem fahrenden Zug unterbringen und dasselbe Experiment dort ausführen, so erwarten wir, dass die Wahrscheinlichkeit für unseren Satz Messwerte sich dadurch nicht ändert. In diesem Fall wäre der Boost des ruhenden Systems in den Zug eine Symmetrietransformation.
Nun wird aber das im Zug fahrende quantenmechanische System sicher nicht mehr durch denselben
Zustandsvektor \( | \psi \rangle \) beschrieben
wie das ruhende System zuvor. Wir werden es mit einem neuen Zustandsvektor
\( | \psi' \rangle \)
zu tun haben.
Und auch die Messwerte werden nicht genau dieselben sein wie zuvor.
Wenn wir im ruhenden System nach der Wahrscheinlichkeit fragen,
einen bestimmten Impuls \(\boldsymbol{p}\) zu messen, so müssen wir bei dem
mitfahrenden System nach einem anderen Impuls \(\boldsymbol{p}'\) fragen, der die Eigenbewegung
des Zuges berücksichtigt. Also werden wir es
auch mit einem neuen Zustandsvektor \( | \phi' \rangle \)
zu tun haben.

Wir haben es also mit einer Symmetrie zu tun, wenn gilt:
| \[ | \langle \phi | \psi \rangle |^2 = | \langle \phi' | \psi' \rangle |^2 \] |
Das ist im Grunde die Definition einer quantenmechanischen Symmetrie.
Für den Wechsel von den alten Zustandsvektoren \( | \psi \rangle \) und \( | \phi \rangle \) zu den neuen (beispielsweise im Zug mitfahrenden oder gedrehten) Zustandsvektoren \( | \psi' \rangle \) und \( | \phi' \rangle \) benötigen wir eine Umrechnungsvorschrift, die ich \( T_g \) nennen möchte. Es gilt also: \[ | \psi' \rangle = T_g \, | \psi \rangle \] \[ | \phi' \rangle = T_g \, | \phi \rangle \] Der Index \( g \) deutet an, dass \( T_g \) von einem Gruppenelement \(g\) aus einer Symmetriegruppe \(G\) abhängt. So könnte \(g\) einen Boost oder eine Drehung darstellen – mehr dazu weiter unten. Der Operator \( T_g \) hängt nicht vom Zustand ab, der umgerechnet werden soll, sondern nur von der Art der Symmetrietransformation \(g\), die durchgeführt wird.
Wenn \( T_g \) ein unitärer Operator ist, dann ändert sich das Skalarprodukt nicht, d.h. dann ist \[ \langle \phi | \psi \rangle = \langle T_g \, \phi | T_g \, \psi \rangle = \langle \phi' | \psi' \rangle \] Damit ändern sich auch die Betragsquadrate und damit die Wahrscheinlichkeiten nicht, d.h. unitäre Operatoren sind dazu geeignet, Symmetrien in der Quantentheorie zu beschreiben.
Was manchmal hier übersehen wird: In den meisten Fällen werden Symmetrien zwar durch unitäre Operatoren dargestellt, aber das ist nicht zwingend. Wir fordern nämlich nicht, dass sich das Skalarprodukt nicht ändern darf, sondern nur, dass sich dessen Betragsquadrat nicht ändert. Die korrekte Aussage lautet so:
|
\(T_g\) ist linear \[ T_g \, ( a \, | \psi \rangle + b \, | \phi \rangle ) = \] \[ = a \, T_g \, | \psi \rangle + b \, T_g \, | \phi \rangle \] und das Skalarprodukt ändert sich also nicht: \[ \langle \phi | \psi \rangle = \langle T_g \, \phi | T_g \, \psi \rangle \]
\(T_g\) ist antilinear \[ T_g \, ( a \, | \psi \rangle + b \, | \phi \rangle ) = \] \[ = a^* \, T_g \, | \psi \rangle + b^* \, T_g \, | \phi \rangle \] und das Skalarprodukt wird umgedreht bzw. komplex konjugiert (der Stern bedeutet dabei das komplexe Konjugieren): \[ \langle \phi | \psi \rangle = \langle T_g \, \psi | T_g \, \phi \rangle = \] \[ = \langle T_g \, \phi | T_g \, \psi \rangle^* \]
Wann gilt nun welche der beiden Alternativen?
Wenn \( T_g \) über das Gruppenelement \(g\) stetig mit \( g = 1 \) verbunden ist, dann können diese Operatoren \( T_g \) unitär gewählt werden (beispielsweise bei Drehungen, Translationen und Boosts). Das bedeutet aber nicht zwingend, dass die \( T_g \) eine unitäre Darstellung der Gruppe bilden, denn man kann zwar für zwei Gruppenelemente \(g\) und \(h\) und ihr Produkt \( h g \) unitäre Operatoren \( T_g , \, T_h \) und \( T_{hg} \) finden, aber es muss nicht zwangsläufig \( T_h T_g = T_{hg} \) sein. Der Operator \( T_g \) muss noch nicht einmal stetig von \(g\) abhängen (siehe Beispiel etwas weiter unten)!
Ein Beispiel für ein anti-unitäres \( T_g \) ist die Zeitspiegelung.
Beim Beweis des Wigner-Theorems kommt es darauf an, dass man die komplexen Phasen der Vektoren geeignet wählen kann, so dass \( T_g \) unitär oder antiunitär wird. Wir erinnern uns: Vektoren, die sich nur durch eine komplexe Phase \( e^{i \alpha} \) unterscheiden, repräsentieren denselben quantenmechanischen Zustand! Der Beweis ist elementar, benötigt aber doch einige Schritte. Man findet ihn beispielsweise hier:
Betrachten wir ein konkretes Beispiel: räumliche Drehungen um die z-Achse un einen Drehwinkel \( \varphi \), die eine Untergruppe der Drehgruppe bilden.
Wir wollen in unserem Beispiel einen sehr einfachen Hilbertraum betrachten, der nur 2 Zustände besitzt, d.h. Vektoren aus diesem Hilbertraum sind zweikomponentige komplexe Vektoren (der Hilbertraum ist also \(\mathbb{C}^2\), wobei \(\mathbb{C}\) die Menge der komplexen Zahlen ist). Wir können uns hier ein Teilchen mit Spin 1/2 vorstellen, das sich in einem quantenmechanischen Superpositionszustand aus den Spinkomponenten +1/2 und −1/2 befindet, wobei wir räumliche Abhängigkeiten nicht betrachten. Den Zustand \( | \psi \rangle \) schreiben wir also als Spaltenvektor \[ \begin{pmatrix} a \\ b \end{pmatrix} \] wobei \(a\) und \(b\) komplexe Zahlen sind. Wie wir später noch sehen werden, führt eine Drehung um die z-Achse für einen solchen Spin-1/2-Zustandsvektor zu der folgenden Umrechnungsformel: \[ T_g \, \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} e^{i \, \varphi/2} a \\ e^{-i \, \varphi/2} b \end{pmatrix} \]
d.h. \( T_g \) ist die folgende komplexe 2-mal-2-Matrix: \[ T_g = \begin{pmatrix} e^{i \, \varphi/2} & 0 \\ 0 & e^{-i \, \varphi/2} \end{pmatrix} \] Die Amplitude \(a\) wird also genau entgegengesetzt zur Amplitude \(b\) gedreht, aber beide nur mit dem halben Drehwinkel \( \varphi \).
Die Drehungen \(g\) in der x-y-Ebene können wir mit komplexen Zahlen \(x + iy\) bequem schreiben als \[ g \, (x + iy) = e^{i \varphi} (x + iy) \] d.h. in dieser Darstellung ist \[ g = e^{i \varphi} \] Der Zusammenhang zwischen \( T_g \) und \(g\) ist demnach gegeben durch \[ T_g^2 = T_g T_g = \begin{pmatrix} g & 0 \\ 0 & g^* \end{pmatrix} \] (der Stern bezeichnet das komplexe Konjugieren). Wir sehen schon: Die Drehung \(g\) legt in dieser Gleichung den Umrechnungsoperator \( T_g \) nicht eindeutig fest. Die Matrix \( -T_g \) erfüllt die Gleichung ebenfalls, denn das negative Vorzeichen fällt beim Quadrieren weg.
Vielleicht fühlt sich mancher Leser hier an die Wurzelfunktion in der Funktionentheorie erinnert. Der Term \( e^{i \, \varphi/2} \) oben in \(T_g\) ist ja gerade die Wurzel von \(g = e^{i \varphi}\), denn \( (e^{i \, \varphi/2})^2 = e^{i \varphi} = g \).
Man kann die Wurzelfunktion auf einer sogenannten Riemannschen Fläche definieren, die die komplexe Ebene zweimal überdeckt – wie eine Wendeltreppe, die zweimal herumführt und bei der man nach zwei Stockwerken wieder in das Ausgangsstockwerk zurückspringt. Der Drehwinkel \( \varphi \) auf dieser Wendeltreppe läuft von \(0\) bis \( 4 \pi \). Die Wendeltreppe (genauer: die Linie im Abstand 1 von der Mittelachse) ist gleichsam die Gruppenmannigfaltigkeit der \( e^{i \, \varphi/2} \)-Gruppe, denn jedem Punkt der Wendeltreppen-Linie kann man eindeutig ein Gruppenelement \( e^{i \, \varphi/2} \) zuordnen. Man sagt auch, die Riemannsche Fläche der Quadratwurzel ist eine doppelte Überlagerung der komplexen Ebene. Ein schönes Bild dazu findet man unter Wikipedia: Riemann surface.
Ist \( T_g \) ein unitärer Operator? So einen Operator muss es ja nach dem Satz von Wigner geben, denn \( T_g \) lässt sich stetig mit der Eins verbinden (dazu muss man nur den Drehwinkel \( \varphi \) auf Null herunterfahren). Prüfen wir es nach und verwenden dazu das übliche Skalarprodukt in \(\mathbb{C}^2\): \[ \langle \psi_1 | \psi_2 \rangle = \] \[ = \bigg{\langle} \begin{pmatrix} a_1 \\ b_1 \end{pmatrix} \bigg{|} \begin{pmatrix} a_2 \\ b_2 \end{pmatrix} \bigg{\rangle} = \] \[ = a_1^* a_2 + b_1^* b_2 \] Dann ist \[ \langle T_g \psi_1 | T_g \psi_2 \rangle = \] \[ = \bigg{\langle} \begin{pmatrix} e^{i \, \varphi/2} a_1 \\ e^{-i \, \varphi/2} b_1 \end{pmatrix} \bigg{|} \begin{pmatrix} e^{i \, \varphi/2} a_2 \\ e^{-i \, \varphi/2} b_2 \end{pmatrix} \bigg{\rangle} = \] \[ = (e^{i \, \varphi/2} a_1)^* \, (e^{i \, \varphi/2} a_2) + \] \[ + (e^{- i \, \varphi/2} b_1)^* \, (e^{- i \, \varphi/2} b_2) = \] \[ = e^{-i \, \varphi/2} a_1^* \, e^{i \, \varphi/2} a_2 + \] \[ + e^{i \, \varphi/2} b_1^* \, e^{- i \, \varphi/2} b_2 = \] \[ = a_1^* a_2 + b_1^* b_2 = \] \[ = \langle \psi_1 | \psi_2 \rangle \] d.h. \( T_g \) ist ein unitärer Operator.
Wenn wir den Drehwinkel \( \varphi \) von \(0\) langsam bis auf den Wert \( 2 \pi \) (also 360 Grad) erhöhern, so landet unsere Drehung \( g = e^{i \varphi} \) wieder beim Eins-Element der Gruppe. Wir haben also einen geschlossenen Weg im Raum unserer Drehungen zurückgelegt.
Nicht so bei \( T_g \) , denn \( T_g \) landet für \( \varphi = 2 \pi \) bei der negativen Einheitsmatrix \( -1 \). Erst wenn wir noch eine zweite Drehung anschließen und \( \varphi \) bis \( 4 \pi \) hochfahren, landen wir wieder beim Ausgangspunkt \( T_g = 1 \) und der Weg im Raum der \( T_g \) schließt sich.
Ein geschlossener Weg in der Gruppe \(G\) (aus der unsere Drehung \(g\) stammt) führt also nicht immer zu einem geschlossenen Weg im Raum der Operatoren \( T_g \). Der tiefere Grund dafür liegt darin, dass wir einen geschlossenen Weg in \(G\) gewählt haben, der sich nicht stetig in \(G\) auf einen Punkt zusammenziehen lässt – wir kommen noch darauf zurück.
Wir hatten bereits angedeutet, dass \( T_g \) von einem Gruppenelement \(g\) aus einer Gruppe \(G\) abhängt – gerade haben wir beispielsweise eine Untergruppe der Drehgruppe betrachtet. Ein anderes Beispiele ist die Gruppe der affinen Abbildungen in der Raumzeit (siehe Kapitel 2.3), die als Untergruppe beispielsweise die Galileigruppe (siehe Kapitel 2.4) und die Poincarégruppe (siehe Kapitel 3.1) umfasst. Die Drehgruppe ist wiederum eine Untergruppe beider Gruppen. Hinzu kommen zu den Drehungen die Raum-Zeit-Translationen sowie nichtrelativistische oder relativistische Boosts.
All diese Gruppen sind Lie-Gruppen, d.h. die Gruppenelemente hängen kontinuierlich von Parametern ab (z.B. Drehwinkel, Boostgeschwindigkeit und Translationsvektor). Präziser kann man sagen: eine Lie-Gruppe ist eine differenzierbare Mannigfaltigkeit mit einer zusätzlichen Gruppenstruktur. Die Parameter fungieren dabei als Koordinaten auf dieser Mannigfaltigkeit. Wir sind darauf bereits in Kapitel 3.5 kurz eingegangen, als wir uns die topologische Struktur der Poincarégruppe (also der entsprechenden Gruppenmannigfaltigkeit) angesehen haben.
Gruppenstruktur bedeutet: Man kann Symmetrietransformationen hintereinander ausführen und erhält wieder eine Symmetrietransformation. Mathematisch kann man dies durch die Multiplikation der Gruppenelemente darstellen.
Betrachten wir ein konkretes Gruppenelement \( g \) , z.B. eine Drehung. Dann gehört dazu in der Quantentheorie ein entsprechender Operator \( T_g \) zum Umrechnen der Zustandsvektoren im Hilbertraum (um das ursprüngliche quantenmechanische System in das gedrehte System umzurechnen). Zu einem anderen Gruppenelement \(h\) (z.B. einer anderen Drehung) gehört ein anderer Operator \( T_h \). Nun führen wir beide Symmetrietransformationen hintereinander aus – erst \(g\), dann \(h\). Entsprechend rechnen wir einen Zustand \( | \psi \rangle \) erst mit \( T_g \) und dann mit \( T_h \) in einen neuen Zustand um.
Alternativ können wir aber auch die beiden Symmetrietransformationen \(g\) und \(h\) durch die zusammengesetzte Symmetrietransformation \( h g \) ersetzen (dabei steht zwischen \(h\) und \(g\) die Multiplikation der Gruppenelemente). So können wir beispielsweise die Drehungen \(g\) und \(h\) durch eine einzige Drehung \( h g \) ersetzen. Der entsprechende Umrechnungsoperator wäre dann \( T_{h g} \).
Muss nun der Umrechnungsoperator \( T_{h g} \) dieselbe Umrechnung von \( | \psi \rangle \) bewirken wie die Hintereinanderschaltung von \( T_g \) und \( T_h \)? Die Antwort lautet: Nicht unbedingt! Es muss nur gewährleistet sein, dass der Zustandsvektor, der bei der Umrechnung herauskommt, in beiden Fällen denselben Quantenzustand repräsentiert. Bei der Wahl eines Zustandsvektors für einen Quantenzustand haben wir jedoch eine gewisse Freiheit: zwei Vektoren, die sich nur durch eine komplexe Phase \( e^{i \alpha} \) unterscheiden, repräsentieren denselben Quantenzustand. Es muss also gelten: \[ T_{h g} \, | \psi \rangle = e^{i \alpha} \, T_h \, T_g \, | \psi \rangle \] Man nennt deshalb die Operatoren \( T_g \) eine Strahldarstellung oder projektive Darstellung der Gruppe. Die Gruppenstruktur überträgt sich bis auf eine komplexe Phase auf die Operatoren.
Dabei kann die Zusatzphase \( \alpha \) von den Gruppenelementen \(g\) und \(h\) abhängen, nicht aber vom Zustand \( | \psi \rangle \) (denn die Symmetrietransformation darf ja Interferenzen zwischen Zuständen nicht ändern) – so zumindest steht es in vielen Texten.
In Steven Weinbergs Buch The Quantum Theory of Fields findet man dazu Genaueres: So stellt man experimentell fest, dass nicht alle Quantenzustände zu neuen Zuständen überlagert werden können (Superauswahlregeln – wir sind bereits im letzten Kapitel 4.5 darauf eingegangen.). So kann man keine Quantenzustände präparieren, die eine Überlagerung von Zuständen mit unterschiedlicher elektrischer Ladung sind. Die elektrische Ladung eines quantenmechanischen Objektes ist immer bekannt, da sie über ihr weitreichendes elektrisches Feld makroskopische Auswirkungen hat. Entsprechend gibt es auch keine Interferenz zwischen Zuständen verschiedener Ladung.
Ähnlich ist es mit dem Gesamtspin: Die Experimente legen nahe, dass es keine Superposition und Interferenz zwischen Zuständen mit halbzahligem und ganzzahligem Spin gibt. Entsprechend könnte die Phase α durchaus vom Quantenzustand abhängen, und zwar von seiner Eigenschaft, ob sein Gesamtspin ganz- oder halbzahlig ist. Man sieht also, dass die Details hier oft gar nicht so klar sind, wie sie manchmal zunächst erscheinen.
Oben bei den Drehungen um die z-Achse haben wir gesehen, dass die Zuordnung der Gruppenelemente \(g = e^{i \varphi}\) zu den Operatoren \(T_g\) nicht ganz eindeutig ist, denn erst die Zuordnung von \(g\) zu \(T_g^2\) (also der doppelten Anwendung von \(T_g\) ) ist eindeutig, denn in der Formel von \(T_g\) kommen die Diagonalelemente \( e^{\pm i \, \varphi/2} \) vor. Nach einer vollen Umdrehung wandern wir von \(T_g = 1\) zu \(T_g = -1\) und erst nach der zweiten Umdrehung dann wieder zurück zu \(T_g = 1\). Für die Strahldarstellung ist das unproblematisch, denn das Vorzeichen ist ja wie eine Zusatzphase. Wenn wir allerdings die Zuordnung von \(g\) zu \(T_g\) eindeutig machen wollten, müssten wir nach einer Umdrehung künstlich von \(T_g = -1\) zu \(T_g = 1\) zurückspringen und die nächste Drehung von dort beginnen. Das könnten wir beispielsweise dadurch machen, dass wir beim Überschreiten von \( \varphi = 2 \pi \) den Drehwinkel wieder auf Null setzen, also in der Formeln von \(T_g\) mit einem Drehwinkel \( \varphi' = (\varphi \, \mathrm{modulo} \, 2 \pi) \) arbeiten.
Insgesamt ist das alles ziemlich unpraktisch. Schöner wäre es, wenn man auf dieses Zurückspringen von \( T_g \) nach einer Umdrehung verzichten könnte. Allerdings würde das bedeuten, dass bei einer Umdrehung \( T_g \) von \(1\) nach \(-1\) wandert, und erst bei der zweiten Umdrehung würde dann \( T_g \) von \(-1\) wieder nach \(1\) wandern.
Damit wäre einer Drehung \(g\) nicht mehr eindeutig ein Operator \( T_g \) zugeordnet, denn in der Gruppe der Drehungen gibt es keinen Unterschied zwischen der ersten und der zweiten Drehung. Also braucht man so etwas wie die Gruppe \(G'\) der Doppeldrehungen, bei der sich die Gruppenelemente der ersten Drehung von denen der zweiten Drehung unterscheiden. So etwas nennt man Überlagerungsgruppe.
Die Wendeltreppe oben ist genau diese Überlagerungsgruppe! Den Gruppenelementen \( g' = e^{i \, \varphi/2} \) der Überlagerungsgruppe kann man dann eindeutig den Operator \(T_{g'}\) zuordnen. Man hat nun allerdings keine direkte Strahldarstellung von \(G\) mehr (in dem Sinn, dass man jedem \(g\) umkehrbar eindeutig ein \(T_g\) zuordnen kann), sondern man hat eine unitäre Darstellung der Überlagerungsgruppe \(G'\). In der Quantenmechanik reicht das aber wegen der Phasen-Mehrdeutigkeit der Zustandsvektoren vollkommen aus.
Wie sieht das im allgemeinen Fall aus? Wir haben Glück, denn man kann zeigen, dass es zu jeder zusammenhängenden Lie-Gruppe \(G\) eine eindeutige universelle Überlagerungsgruppe gibt, die zudem topologisch einfach zusammenhängend ist, d.h. man kann jeden geschlossenen Weg in der Gruppenmannigfaltigkeit stetig zu einem Punkt zusammenziehen und man kann zwei verschiedene Wege mit gleichem Start- und Endpunkt stetig ineinander umformen (siehe dazu auch Die Grenzen der Berechenbarkeit, Kapitel 5.3: Die 3-Sphäre und die Poincaré-Vermutung).
Das ist günstig, denn in unserem Beispiel oben haben wir ja gerade gesehen, dass diejenigen geschlossenen Wege Probleme machen, bei denen das nicht geht. Die Drehgruppe und mit ihr die Galileigruppe und die Poincarégruppe sind nämlich nicht einfach zusammenhängend (siehe Kapitel 3.5). Eine Drehung um den Winkel \(0\) ist gleichwertig zu einer Drehung um den Winkel \(2 \pi\) (eine volle Drehung). Geht man langsam alle Drehwinkel von Null bis \(2 \pi\) durch, so erhält man einen geschlossenen Weg im Raum der Gruppenelemente, den man nicht stetig auf einen Punkt (ein Gruppenelement) zusammenziehen kann.
Den Begriff der Überlagerungsgruppe wollen wir noch präzisieren:
|
universelle Überlagerungsgruppe: Zu jeder (zusammenhängenden) Lie-Gruppe \(G\) gibt es eine eindeutige universelle Überlagerungsgruppe \(G'\), die einfach zusammenhängend ist (d.h. geschlossene Wege darin lassen sich stetig zu einem Punkt zusammenziehen). Eindeutig bedeutet dabei: Jede andere zusammenhängende Lie-Gruppe, die dieselbe Lie-Algebra wie \(G\) hat, hat dieselbe universelle Überlagerungsgruppe wie \(G\). Auch die universelle Überlagerungsgruppe \(G'\) selbst hat diese Lie-Algebra. Zum Begriff der Lie-Algebra kommen wir etwas weiter unten. Überlagerung bedeutet: Man kann die Überlagerungsgruppe G' gleichsam über die Gruppe G legen und G damit komplett abdecken, wobei ein mehrlagiges Abdecken erlaubt ist. Mathematisch ausgedrückt: Es gibt eine surjektive Projektion \[ \rho: \, G' \rightarrow G \] die mit der Gruppenstruktur verträglich ist (d.h. \(\rho\) ist ein Gruppenhomomorphismus): \[ \rho(h') \, \rho(g') = \rho(h' \, g') \] mit \(g'\) und \(h'\) aus der Überlagerungsgruppe \(G'\). Surjektiv heißt: Zu jedem Gruppenelement aus \(G'\) gibt es ein eindeutiges Gruppenelement aus \(G\), und zu jedem Gruppenelement aus \(G\) gibt es ein oder mehrere Gruppenelemente aus \(G'\). Es kann also sein (und ist auch meist so), dass mehrere (meist zwei) Gruppenelemente der Überlagerungsgruppe \(G'\) zum selben Gruppenelement von \(G\) gehören. Die Projektion \(\rho\) hat die Eigenschaft, dass ihr Kern (also die Urbilder die Zielelements \(1\)) eine endliche Gruppe ist. Die Elemente der Überlagerungsgruppe \(G'\), die zum Eins-Element von \(G\) gehören, bilden also eine endliche Gruppe (typischerweise bestehend aus den Elementen \(1\) und \(-1\)). |
Den Begriff der Lie-Algebra, der oben erwähnt wird, müssen wir noch erklären. Abstrakt ist die Lie-Algebra gegeben durch den Tangentialraum der Lie-Gruppe im Einselement, wobei die Lie-Klammer eine multiplikative Struktur liefert. Diese Formulierung ist allerdings etwas gewöhnungsbedürftig. In den meisten Fällen kann man jedoch Elemente der Lie-Algebra einfach als Matrizen schreiben, und zwar dann, wenn die Gruppe g eine Matrixgruppe ist, d.h. wenn jedes Gruppenelement \(g\) als Matrix geschrieben werden kann. Tatsächlich gilt, dass jede Liegruppe zumindest lokal zu einer Matrixgruppe isomorph (also gleichwertig) ist.
Auch Poincarégruppe und Galileigruppe können als Matrixgruppen geschrieben werden. Erinnern wir uns: Ein Gruppenelement \(g\) ist bei diesen Gruppen zunächst durch eine 4-mal-4-Matrix \(A\) und einen Translations-Vierervektor \(c\) eindeutig gekennzeichnet, denn die Wirkung auf die Raumzeit ist durch die Abbildung \[ g x := A x + c \] gegeben. Die Gruppenmultiplikationsregel können wir dann leicht ausrechnen: \[ g' g x = \] \[ =A' (A x + c) + c' = \] \[ = A' A x + A c + c' = \] \[ =: A'' x + c'' = \] \[ =: g'' x \] d.h. das Gruppenelement \( g'' = g' g \) wird durch die 4-mal-4-Matrix \( A'' = A' A \) und den Translationsvektor \( c'' = A c + c' \) gekennzeichnet. Genau das können wir erreichen, wenn wir \(g\) durch die 5-mal-5-Matrix \[ g = \begin{pmatrix} A & c \\ 0 & 1 \end{pmatrix} \] darstellen (analog für \(g'\) und \(g''\), wobei wir keine neue Bezeichnung für die Matrix eingeführt haben), denn dann ergibt die Matrixmultiplikation genau den gewünschten Zusammenhang für die Gruppenmultiplikation. Die Wirkung auf die Raumzeit können wir darstellen, indem wir die \(g\)-Matrix auf den 5-komponentigen Vektor \( (x, 1) \) wirken lassen. Die 5-te Dummy-Komponente (also die \(1\)) ändert sich dabei nicht.
Für jeden reellen Gruppenparameter \( a^i \) (z.B. Drehwinkel; wir schreiben den Parameter-Index hier oben wegen der engen Verbindung zur Differenzialgeometrie) können wir nun direkt einen Tangentialvektor \(A_i\) im Einselement der Gruppe definieren, wobei es in der Physik üblich ist, einen Faktor \( - i \) (die negative imaginäre Einheit) einzufügen (ist in der Quantentheorie nützlich, da man so später hermitesche Operatoren erhält). Die Bezeichnungen \( a^i \) und \(A_i\) haben übrigens nichts mit dem gerade verwendeten \(A\) im Term \( A x + c \) zu tun. Es ist also: \[ A_i := -i \frac{\partial g}{\partial a^i} \bigg|_{a = 0} \] wobei \(g\) als Matrix zu sehen ist, die von den Gruppenparametern \(a = (a^i)\) abhängt, und wir \( g(0) = 1 \) voraussetzen (Vorsicht: die hoch- und tiefgestellten i-s sind natürlich Indices, das davorstehende \(i\) ist die imaginäre Einheit).
Man bezeichnet die \( A_i \) als Generatoren der Lie-Gruppe, denn die Kommutatoren der \( A_i \) legen die Gruppenstruktur der Lie-Gruppe zumindest in der Nähe des 1-Elementes fest (dabei ist der Kommutator zweier Matrizen definiert durch \[ [A, B] := A B - B A \] Das liegt daran, dass man in einer Umgebung des 1-Elementes die Gruppenelemente schreiben kann als \[ g(a) = e^{i a^i A_i} = 1 + i \, a^i A_i - \frac{1}{2} \, a^i A_i \, a^j A_j + \, .... \] (mit Summation über doppelte Indices). Die Exponentialfunktion ist also durch die übliche Reihenentwicklung definiert. Diese Reihenentwicklung konvergiert immer für Matrizen (siehe Wikipedia: Matrixexponential ). Für das Produkt von zwei Exponentialreihen gilt nun die Baker-Campbell-Hausdorff-Formel: \[ e^A \, e^B = e^{A + B + \frac{1}{2} [A, B] + \frac{1}{12} [[A, B], B] - \frac{1}{12} [[A, B], B] + \, ...} \] wobei die Punkte unendlich viele komplexere, ineinander geschachtelte Kommutatorterme andeuten, in denen \(A\) und \(B\) immer öfter vorkommen. Für \(A\) und \(B\) kann man nun Elemente der Lie-Algebra einsetzen (also reelle Linearkombinationen der Form \( a^i A_i \) mit Summe über \(i\) ) und erhält so links das Produkt zweier Gruppenelemente der Lie-Gruppe. Dieses Produkt ist nun durch die obige Formel dann eindeutig festgelegt, wenn die unendliche Summe von Kommutatoren im Exponenten rechts konvergiert. Das ist insbesondere dann der Fall, wenn die Gruppenparameter \(a^i\) klein sind, denn in der Summe tauchen immer höhere Potenzen der Parameter auf. Damit legen die Kommutatoren der Generatoren bei kleinen Gruppenparametern fest, wie aus der Multiplikation zweier Gruppenelemente ein neues Gruppenelement entsteht, d.h. die Lie-Algebra legt die Gruppenstruktur zumindest in der Nähe des 1-Elementes fest.
Wenn zwei Gruppen dieselbe Lie-Algebra haben, bedeutet das also, dass die Gruppen in der Nähe des Eins-Elementes gleich aussehen. Genau genommen sehen die Gruppen dann sogar überall lokal gleich aus, denn die Nähe eines Gruppenelementes \(g\) erreicht man ja durch Multiplikation mit einem Gruppenelement \(h\) aus der nahen Umgebung des Eins-Elementes.
Man könnte sich nun vorstellen, dass man viele kleine Gruppenelemente (also Elemente aus der Nähe der Eins) multipliziert und so zu immer größeren Gruppenelementen gelangt, also zu Gruppenelementen, die immer weiter weg von der Eins liegen. So könnte man sich mit vielen kleinen Drehungen zu immer größeren Drehungen vorarbeiten.
Diese größeren Gruppenelemente sind dann Produkte vieler kleinerer Gruppenelemente, die sich wiederum jeweils als Exponentialreihe schreiben lassen. Man kann sich vorstellen, dass man auf diese Weise alle Gruppenelemente erreicht, die sich stetig mit der Eins verbinden lassen (also die Zusammenhangskomponente der Gruppe mit dem Einselement).
Tatsächlich lässt sich jedes Gruppenelement einer zusammenhängenden Lie-Gruppe als endliches Produkt von Exponentialreihen schreiben. (es reichen sogar nur zwei Exponentialreihen, wie M.Moskowitz und R.Sacksteder in 2003 gezeigt haben). Nach der Baker-Campbell-Hausdorff Formel oben müsste sich daraus eigentlich eine einzige Exponentialreihe machen lassen, aber man weiß nicht, ob die unendliche Summe von Matrixkommutatoren im Exponenten auf der rechten Seite immer konvergiert! Ist die Lie-Gruppe zusätzlich noch kompakt, so sind die Parameterbereiche zumeist endliche abgeschlossene reelle Intervalle – die Parameter werden also nicht beliebig groß. Die Baker-Campbell-Hausdorff Formel ist dann tatsächlich in der Lage, Produkte von Exponentialreihen zu einer einzigen Exponentialreihe zu vereinen, so dass die Exponentialabbildung sogar surjektiv ist, d.h. jedes Gruppenelement kann als Exponentialreihe geschrieben werden. Siehe dazu u.a. Wikipedia: Lie group, speziell den Abschnitt The exponential map.
Der Begriff der Algebra im Wort Lie-Algebra bezieht sich auf den Kommutator, denn dieser wirkt wie ein Produkt innerhalb der Lie-Algebra: \[ [A_i, A_j] = i \, f^k_{\, ij} \, A_k \] (mit Summierung über doppelte Indices) mit den reellen Strukturkonstanten \(f^k_{\, ij}\), die durch diese Gleichung definiert werden (das \(i\) hinter dem Gleichheitszeichen ist wieder die imaginäre Einheit).
Diese Strukturkonstanten erfassen also die Kommutator-Struktur der Lie-Algebra. Dass \( [A_i, A_j] \) tatsächlich in der Lie-Algebra (also im Tangentialraum der Gruppe bei \(1\)) liegt und sich demnach als Linearkombination der \( A_k \) schreiben lässt, sieht man so:
Der Term \[ e^{i s A_j} \, e^{i t A_i} \, e^{- i s A_j} \] ist für festes reelles \(s\) eine Kurve im Gruppenraum mit dem reellen Kurvenparameter \(t\), die bei \(t=0\) durch das Einselement läuft. Die Ableitung dieser Kurve nach \(t\) bei \(t=0\) ergibt also ein Element des Tangentialraums am Einselement, und zwar dieses: \[ \frac{d}{dt} \, e^{i s A_j} \, e^{i t A_i} \, e^{- i s A_j} \, \bigg|_{t=0} = \] \[ = e^{i s A_j} \, i A_i \, e^{- i s A_j} \] Dieser Ausdruck stellt nun eine Kurve im Tangentialraum der \(1\) mit Kurvenparameter \(s\) dar. Man kann diese Kurve nun nach \(s\) in \(s=0\) ableiten und erhält wieder einen Tangentialvektor (innerhalb eines Vektorraums ergibt die Differenz von Vektoren ja wieder einen Vektor, und so ist es auch im Differentialquotienten bei der Ableitung). Der Tangentialvektor lautet: \[ \frac{d}{ds} \, e^{i s A_j} \, i A_i \, e^{- i s A_j} \, \bigg|_{s=0} = \] \[ = i A_j \, i A_i + i A_i (-i A_j) = \] \[ = A_j A_j - A_j A_i = [A_i , A_j] \] Wichtig ist dabei: Obwohl der Kommutator \( [A_i , A_j] \) im Tangentialraum liegt, gilt dies nicht für Produkte der Generatoren. Das Produkt \( A_i A_j \) liegt im Allgemeinen nicht im Tangentialraum der Gruppe im Einselement.
Eine Darstellung der Lie-Algebra auf einem Hilbertraum sind nun lineare Operatoren \( T(A_i) \) , die \[ [T(A_i), T(A_j)] = i \, f^k_{\, ij} \, T(A_k) \] erfüllen. Unten werden wir auf Strahldarstellungen der Lie-Algebra treffen, bei denen dabei noch ein Zusatzterm auftritt. Vorsicht: Wir haben nicht \( T(A_i) T(A_j) = T(A_i A_j) \) gefordert – der Term rechts wäre gar nicht definiert, denn das Produkt \( A_i A_j \) liegt i.a. gar nicht im Tangentialraum.
Die (Strahl-)Darstellung \( T_{g(a)} \) einer Lie-Gruppe ergibt automatisch eine (Strahl-)Darstellung \( T(A_i) \) der Lie-Algebra über die Formel \[ T(A_i) := -i \frac{\partial}{\partial a^i} T_{g(a)} \bigg|_{a = 0} \] Umgekehrt ergibt eine (Strahl-)Darstellung der Lie-Algebra auch eine (Strahl-)Darstellung der Gruppe über die Formel \[ T_{g(a)} := e^{i \, a^i \, T(A_i)} \] (mit Summe über den Index \(i\)).
Wichtig ist nun der folgende Zusammenhang: Wenn \( T_{g(a)} \) unitär ist, so ist \( T(A_i) \) hermitesch und umgekehrt. Das sieht man so: Wir definieren zu einem Operator \( A \) den dazu hermitesch adjungierten Operator \( A^+ \) über die Gleichung \[ \langle A^+ \phi | \psi \rangle := \langle \phi | A \psi \rangle \] Wenn wir \(A\) als (unendlich-dimensionale) Matrix schreiben (siehe vorheriges Kapitel), so wäre \(A^+\) dann die transponierte und komplex konjugierte Matrix. A ist hermitesch, wenn \(A^+ = A\) ist, und \(A\) ist unitär, wenn \( A^+ A = 1 \) ist.
Wenn nun \( U := e^{i t A} \) unitär ist, so können wir die Gleichung \( U^+ U = 1 \) nach \(t\) in \(t=0\) ableiten und erhalten \( -i A^+ + i A = 0 \) und damit \( A^+ = A\), d.h. \(A \) ist hermitesch.
Umgekehrt: Wenn \( A \) hermitesch ist, so ist \( U^+ U = e^{-i t A^+} \, e^{i t A}\) \( = e^{-i t A} \, e^{i t A} = 1 \) und \(U\) ist unitär.
Für \(A\) können wir nun eine Linearkombination \( A = a^i T(A_i) \) (mit Summe über \(i\) und beliebigen reellen \(a^i\) ) einsetzen und \(t = 1\) wählen, so dass \( U = T_{g(a)} \) ist. \(A\) ist genau dann hermitesch, wenn die \(T(A_i)\) hermitesch sind. Damit folgt: Die Generator-Operatoren \(T(A_i)\) sind genau dann hermitesch, wenn der Gruppenoperator \(T_{g(a)}\) unitär ist.
Nun wissen wir aus dem vorherigen Kapitel, dass beobachtbare Größen (Observable) durch hermitesche Operatoren dargestellt werden. Die hermiteschen Darstellungsoperatoren \(T(A_i)\) der Generatoren \(A_i\) einer Symmetriegruppe sind also gute Kandidaten für beobachtbare Größen in der zugehörigen Quantentheorie.
Eine Analyse des Eigenwertspektrums der Operatoren \(T(A_i)\) ergibt dabei die möglichen Messwerte. Interessant ist dabei, dass die Kommutatoren (also die Struktur der Lie-Algebra und damit die lokale Struktur der Symmetriegruppe) dieses Eigenwertspektrum bereits festlegen, wie wir noch sehen werden. Heute geht man meist davon aus, dass alle Observablen in einer Quantentheorie zu Generatoren einer entsprechenden Symmetriegruppe gehören. Dabei können neben der Raum-Zeit-Symmetrie noch weitere Symmetrien auftreten, z.B. Eichsymmetrien. Die Symmetriegruppen bestimmen dann komplett die Struktur der zugehörigen Quantentheorie (Hilbertraum plus Observablen mit ihrem Eigenwertspektrum).
Der Begriff der Überlagerungsgruppe sieht vielleicht noch etwas abstrakt aus. Wir werden aber später anhand von Beispielen sehen, dass es eigentlich recht einfach ist. Beispielsweise ist \(SU(2)\) die Überlagerungsgruppe der Drehgruppe \(SO(3)\), wobei die beiden \(SU(2)\)-Elemente \(1\) und \(-1\) zum \(1\)-Element von \(SO(3)\) gehören. Ein Spinor (eines Spin-1/2-Teilchens) wird bei Drehungen mit der entsprechenden \(SU(2)\)-Matrix umgerechnet, und eine 360-Grad-Drehung führt zur SU(2)-Matrix \(-1\). Genau das haben wir am Beispiel der Drehungen um die z-Achse bereits gesehen. Details dazu im nächsten Kapitel.
Schauen wir uns noch einmal die Drehungen um die z-Achse an und wiederholen das Wichtigste: Zu einer Drehung \[ g = e^{i \varphi} \] gehört einfach das Gruppenelement \[ g' = e^{i \, \varphi/2} \] aus der Überlagerungsgruppe, und die Projektion \(\rho\) ist einfach definiert durch die Gleichung \[ \rho(g') := (g')^2 = g \] Die beiden Gruppelemente \(g'\) und \(-g'\) führen dabei zur selben Drehung \(g\). Der Kern von \(\rho\) ist also durch \(1\) und \(-1\) gegeben, d.h. die beiden Gruppenelemente \(1\) und \(-1\) aus der Überlagerungsgruppe \(G'\) gehören zur Drehung \( g = 1 \) (also Drehwinkel Null oder 360 Grad).
Das Beispiel zeigt sehr schön, wie die Drehungen um die z-Achse durch die Gruppe \(G'\) überlagert wird: Wenn wir den Drehwinkel \( \varphi \) von \(0\) auf \(4 \pi\) hochfahren, so startet \( g' = e^{i \, \varphi/2} \) aus der Überlagerungsgruppe bei \(1\), erreicht bei \( 2\pi \) die \( -1 \) und kommt erst bei \( 4 \pi \) wieder bei \(1\) an. Dabei durchläuft das zugehörige \( g = e^{i \varphi} \) aber 2 komplette Drehungen. In diesem Sinn liefert die Überlagerungsgruppe \(G'\) tatsächlich die gewünschten Doppeldrehungen, denn \(g'\) weiß, ob es sich noch in der ersten oder schon in der zweiten Drehung des zugehörigen \(g\) befindet. Die Projektion \( \rho \) vergisst diese Information gleichsam.
Wir hatten oben bereits die Überlagerungsgruppe \(G'\) als Linie auf einer Wendeltreppe (Riemannsche Fläche) dargestellt und senkrecht darunter die Gruppe \(G\) der Drehungen um die z-Achse als Kreis dargestellt. Die Abbildung \(rho\) entspricht dann der senkrechten Projektion von der Wendeltreppenlinie herunter auf den Kreis.
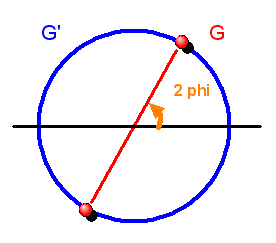
Man kann diesen Zusammenhang aber grafisch auch noch etwas anders darstellen.
Dazu zeichnen wir die Überlagerungsgruppe \(G'\) diesmal als Kreis, wobei der Kreiswinkel durch
\( 2 \varphi \) gegeben ist – man muss also mit \( \varphi \)
von \(0\) bis \(4 \pi\) laufen, um den ganzen Kreis
zu durchlaufen. Die Gruppe \(G\) kann man nun erhalten, indem man gegenüberliegende Punkte
des Kreises miteinander identifiziert. Ein gegenüberliegendes Punktepaar (also \(g'\) und \(-g'\))
entspricht also derselben Drehung \(g\) um die z-Achse.
Dreht man das Punktepaar um 180 Grad (\(\varphi\) läuft also von \(0\) bis \(2 \pi\)),
so erhält man wieder das ursprüngliche Punktepaar
zurück (die beiden Punkte werden ja nicht unterschieden).
Auch bei komplexeren Gruppen ist der Zusammenhang zwischen Überlagerungsgruppe \(G'\) und überlagerter Gruppe \(G\) ähnlich. Die Überlagerungsgruppe entspricht einem einfach zusammenhängenden Raum (z.B. einer Kugeloberfläche), und man identifiziert gewisse Punkte so miteinander, dass dies mit der Gruppenstruktur verträglich ist – so erhält man alle überlagerten Gruppen \(G\) mit diesem \(G'\) als Überlagerungsgruppe. Dieses Bild macht klar, dass die Gruppen lokal gleich aussehen, aber nicht global.
Die obige Beispiel-Gruppe \(G'\) liefert auch eine Strahldarstellung der Drehungen um die z-Achse auf den 2-komponentigen komplexen Vektoren. Wir definieren dazu mit Hilfe von \[ T_{g'} \, \begin{pmatrix} a \\ b \end{pmatrix} := \begin{pmatrix} g' \, a \\ g'^* \, b \end{pmatrix} \] zunächst eine Darstellung von \(G'\). Wie können wir \( T_{g'} \) nun mit der Strahldarstellung \( T_g \) von oben in Verbindung bringen? Ganz einfach: Für \( 0 \le \varphi \lt 2 \pi \) ist \( T_{g'} = T_g \), und für \( 2 \pi \le \varphi \lt 4 \pi \) ist \( T_{g'} = - T_g \).
Anmerkung: Falls Sie sich fragen, ob \(G'\) im obigen Beispiel einfach zusammenhängend ist: Wir haben \(G'\) einfach als Untergruppe einer größeren Gruppe herausgefischt. Diese größere Gruppe – die universelle Überlagerungsgruppe \(SU(2)\) der Drehgruppe \(SO(3)\) – ist einfach zusammenhängend, wie wir in einem späteren Kapitel noch sehen werden. In unserem Beispiel haben wir also in \(G = SO(3)\) die Drehungen um die z-Achse als einparametrige Untergruppe herausgenommen und aus der Überlagerungsgruppe \(G' = SU(2)\) dann die zugehörige einparametrige Untergruppe herausgefischt.
Es gibt auch Situationen, in denen nur die Drehungen um die z-Achse eine Symmetrie des Systems sind (z.B. bei einem äußeren Magnetfeld in z-Richtung). Dann ist tatsächlich \(SO(2)\) die Symmetriegruppe und nicht \(SO(3)\), und wir würden nach der universellen Überlagerungsgruppe von \(SO(2)\) fragen. Diese Überlagerungsgruppe von SO(2) ist \( \mathbb{R} \) mit der Addition als Gruppenverknüpfung. Das liegt einfach daran, dass \(SO(2)\) eine einparametrige Gruppe ist und dass \( g(\varphi) =: \rho(\varphi) \) direkt die Projektion von \( \mathbb{R} \) nach \(SO(2)\) liefert. Man muss also auf \( \mathbb{R} \) die Punkte im Abstand von \( 2 \pi \) miteinander identifizieren, um nach \(SO(2)\) zu gelangen.
Die irreduzible Darstellung von \( \mathbb{R} \) ist \[ T_{g(\varphi)} = e^{i s \varphi} \] mit einem beliebigen reellen \(s\). Man sagt deshalb auch, der Spin \(s\) ist in 2 Dimensionen nicht quantisiert. So etwas ist tatsächlich für die Beschreibung von quantenmechanischen Systemen in einem äußeren Magnetfeld interessant (siehe Anyonen sowie Klaus Fredenhage: Quantenmechanik II, S.52).
Nehmen wir an, wir haben eine Strahldarstellung der Überlagerungsgruppe \(G'\) auf dem Hilbertraum, d.h. \[ T_{h' g'} = e^{i \, \alpha(h',g')} \, T_{h'} , T_{g'} \] (noch können wir nicht sicher sein, dass die Phase unnötig ist, also nehmen wir sie lieber erst einmal mit). Schauen wir uns an, was geschieht, wenn zwei Gruppenelemente \(g'\) und \(h'\) zum selben \(g\) gehören – in diesem Fall wollen wir \(g''\) statt \(h'\) schreiben. Es soll also \[ \rho(g') = \rho(g'') = g \] sein. Da \(\rho\) mit der Gruppenstruktur verträglich ist, gilt: \[ \rho(g' \, g''^{-1}) = \] \[ = \rho(g') \, \rho(g''^{-1}) = \] \[ = \rho(g') \, [\rho(g'')]^{-1} = \] \[ = g \, g^{-1} = 1 \] d.h. \( g' \, g''^{-1} \) gehört zum Kern von \(\rho\). Nennen wir \[ g' \, g''^{-1} =: e' \] d.h. \( \rho(e') = 1 \). Freigestellt nach \(g'\) haben wir dann \[ g' = e' \, g'' \] Fassen wir zusammen: Wenn \( \rho(g') = \rho(g'') = g \) ist, dann gibt es ein Element \(e'\) aus dem Kern von \(\rho\) (also \( \rho(e') = 1 \) ) mit \[ g' = e' \, g'' \] In unserem Beispiel war \(e\) entweder \(1\) oder \(-1\). Aus \( g' = e' \, g'' \) und der Strahldarstellungseigenschaft folgt: \[ T_{g'} = T_{e' \, g''} = e^{i \, \alpha(e',g'')} \, T_{e'} T_{g''} \] Jetzt wird es ein wenig kniffelig. Man muss voraussetzen, dass man eine irreduzible Darstellung der Überlagerungsgruppe hat. Das bedeutet, dass man von jedem Vektor des Hilbertraums jeden anderen Vektor über einen Transformationsoperator erreichen kann. Es darf also keine Unter-Hilberträume geben, die sich nur in sich transformieren. Ggf. muss man eben einen solchen Unter-Hilbertraum als Darstellungsraum nehmen. Dann muss man noch zeigen, dass \( T_{e'} \) und \( T_{g''} \) vertauschen und das zweite Schursche Lemma anwenden. Und schließlich muss man noch verwenden, dass man nach dem Satz von Wigner die \( T_{g'} \) und damit T_{e'} unitär wählen kann. Als Ergebnis erhält man, dass \[ T_{e'} = e^{i \, \beta(e')} \] ist.
Wir können nun aus der Überlagerungsgruppe einen Teilraum herausgreifen, der sich eindeutig auf \(G\) abbilden lässt (beispielsweise die Drehwinkel \( 0 \le \varphi < 2 \pi \) ). Man kann sich vorstellen, dass es sich gleichsam um die erste Überlagerungsschicht handelt. Die anderen Überlagerungsschichten in \(G'\) lassen sich dann aus dieser ersten Schicht durch Multiplikation mit den verschiedenen \(e'\) aus dem Kern von \(\rho\) erzeugen.
Bezeichnen wir das zu \(g\) gehörende eindeutige Element aus der ersten Überlagerungsschicht als \(g'\). Für die Gruppenelemente \(g\) definieren wir die Darstellung einfach durch die Darstellung des entsprechenden eindeutigen \(g'\) (genau so haben wir es auch ganz oben bei den Drehungen um die z-Achse gemacht): \[ T_g := T_{g'} \] Für ein anderes Gruppenelement \(g''\), das auch zu \(g\) gehört, können wir nun \( T_{e'} = e^{i \, \beta(e')} \) mit einem passenden \(e'\) aus dem Kern von \(\rho\) verwenden: \[ T_g := T_{g'} = \] \[ = e^{i \, \alpha(e',g'')} \, T_{e'} T_{g''} = \] \[ = e^{i \, \alpha(e',g'')} \, e^{i \, \beta(e')} T_{g''} \] Freigestellt nach \( T_{g''} \) ergibt sich: \[ T_{g''} = e^{-i \, \alpha(e',g'')} \, e^{-i \, \beta(e')} \, T_g \] g.h. die Darstellungsoperatoren der ursprünglichen Gruppenelemente und der zugehörigen Überlagerungs-Gruppenelemente unterscheiden sich nur um eine Phase. Allerdings hängt diese Phase von \(e'\) und \(g''\) ab. Daher lässt sich die Strahldarstellung von \(G'\) nicht unmittelbar eins-zu-eins in eine Strahldarstellung von \(G\) umschreiben, bei der die Phase nur von \(g\) und \(h\) (statt von \(g'\) und \(h'\) bzw. \(g''\) und \(h''\)) abhängt. Es ist (zumindest mir) aber auch nicht klar, ob das notwendig ist. So hatten wir oben ja bereits angemerkt, dass wegen der Superauswahlregeln die Phase bei der Strahldarstellung von \(G\) auch von Zustandsklassen abhängen kann – deshalb wurde bei der Herleitung eben auch die Forderung nach einer irreduziblen Darstellungen erhoben, bei der man sich nämlich auf so eine Zustandsklasse beschränkt. Offenbar ist hier eine weitere sorgfältige Analyse notwendig, die beispielsweise auch bestimmte Superauswahlregeln zur Folge haben kann. Wesentlich ist, dass ein Darstellungsoperator die Phasen von Zustandsvektoren, die sich superponieren (also addieren) lassen, in gleicher Weise ändert. Zustandsvektoren, bei denen er das nicht tut, darf man nicht zu neuen Zustandsvektoren addieren, wenn der Darstellungsoperator eine Symmetrie sein soll. Bei Drehungen wird das zur Folge haben, dass man ganzzahlige und halbzahlige Spinzustände nicht superponieren kann, wenn man von \(SU(2)\) als Symmetriegruppe ausgeht.
Weitere Infos dazu findet man in Steven Weinbergs Buch The Quantum Theory of Fields, Vol. 1, insbesondere in Kapitel 2.7. Wir gehen im Folgenden einfach davon aus, dass eine Strahldarstellung der Überlagerungsgruppe \(G'\) auch eine Strahldarstellung der ursprünglichen Gruppe \(G\) impliziert. Feinheiten kann man sich dann am konkreten Beispiel ansehen, und das werden wir insbesondere bei der Drehgruppe in einem späteren Kapitel auch tun.
Die Überlagerungsgruppe ist einfach zusammenhängend. Daher können wir die Gruppenelemente \(g'\) immer über einen Weg mit dem Einselement verbinden. Der Satz von Wigner sagt dann, dass die Operatoren \( T_{g'} \) unitär gewählt werden können. Wir wissen aber noch nicht, ob wir auch eine unitäre Darstellung der Überlagerungsgruppe auf dem Hilbertraum erreichen können, d.h. ob wir in jeder Strahldarstellung die Phase weglassen können und \[ T_{h' \, g'} = T_{h'} \, T_{g'} \] schreiben dürfen. Das wäre natürlich eine deutliche Vereinfachung. Eine Analyse zeigt:
Es hängt von der Überlagerungsgruppe ab, ob man die Phase in jeder Strahldarstellung dieser Überlagerungsgruppe weglassen kann und eine unitäre Darstellung erreichen kann. Bei der Überlagerungsgruppe der Drehgruppe oder der Poincarégruppe geht das, bei der Überlagerungsgruppe der Galileigruppe dagegen nicht. Hier eine kurze Zusammenfassung (steht in Steven Weinbergs QFT-Buch ausführlich drin):
Man beginnt mit einer beliebigen Strahldarstellung der Überlagerungsgruppe \[ T_{h' \, g'} = e^{i \, \alpha(h',g')} \, T_{h'} T_{g'} \] und entwickelt die Operatoren sowie die Phase in eine Taylorreihe nach den Parametern der Gruppe – so kommen die Darstellungsoperatoren der Generatoren \( T(A_i) \) der Gruppe ins Spiel, also die Elemente der Lie-Algebra (siehe oben). Dabei entsteht eine lineare Strahldarstellung dieser Generatoren aus der Strahldarstellung der Gruppenelemente über die Gleichung \[ T(A_i) := -i \frac{\partial}{\partial a^i} T_{g(a)} \bigg|_{a = 0} \] Für den Kommutator der Strahldarstellungen der Generatoren erhält man die Gleichung \[ [T(A_i), T(A_j)] = i \, f^k_{\,ij} \, T(A_k) + i \, C_{ij} \, 1 \] (mit Summierung über doppelte Indices) mit den reellen Strukturkonstanten \( f^k_{\,ij} \) (siehe oben) und den sogenannten Zentralladungen der Strahl-Lie-Algebra \( C_{ij} \).
Über die Exponentialdarstellung sieht man mit Hilfe der Baker-Campbell-Hausdorff-Formel (siehe oben), dass es der Term \( i \, C_{ij} \, 1 \) ist, der zur Phase in der Strahldarstellung der Gruppe führt. Wegen diesem Zusatzterm spricht man bei den \(T(A_k)\) auch von einer Strahldarstellung (oder projektiven Darstellung) der Lie-Algebra.
In bestimmten Fällen kann man nun die Darstellungen der Generatoren \(T(A_i)\) so umdefinieren, dass dieser störende Term verschwindet, so dass man eine richtige Darstellung der Lie-Algebra erhält. In diesen Fällen kann man die Phase in jeder Strahldarstellung der Gruppe eliminieren und eine unitäre Darstellung der Überlagerungsgruppe erreichen. Dass man wirklich eine unitäre Darstellung erreichen kann, erfordert noch eine gewisse Sorgfalt, wobei auch wichtig ist, dass die Überlagerungsgruppe einfach zusammenhängend ist – siehe Steven Weinberg: The Quantum Theory of Fields, Vol. 1. Halten wir fest:
|
Satz von Wigner-Bargmann: Wir betrachten eine einfach zusammenhängende Lie-Gruppe \(G'\) (z.B. eine universelle Überlagerungsgruppe) und wir betrachten eine beliebige Strahldarstellung ihrer Lie-Algebra, d.h. es gilt \[ [T(A_i), T(A_j)] = i \, f^k_{\,ij} \, T(A_k) + i \, C_{ij} \, 1 \] Nun untersuchen wir, ob man die Operatoren \(T(A_i)\) so umdefinieren kann, dass die umdefinierten Operatoren \(T'(A_i)\) eine (richtige) Darstellung der Lie-Algebra bilden: \[ [T'(A_i), T'(A_j)] = i \, f^k_{\,ij} \, T'(A_k) \] so dass also keine Zusatzsummanden proportional zum Eins-Operator mehr auftreten (also keine Zentralladungen). Wenn das geht, dann kann man die Phase der Strahldarstellung in die Darstellungsoperatoren der Gruppe integrieren und damit jede Strahldarstellung in eine gleichwertige unitäre Darstellung der Gruppe \(G'\) auf dem Hilbertraum umwandeln, d.h. man kann lineare unitäre Operatoren finden, für die gilt: \[ T_{h' \, g'} = T_{h'} \, T_{g'} \] Bei einer Gruppe \(G\) mit Überlagerungsgruppe \(G'\) erzeugt die unitäre Darstellung der Überlagerungsgruppe \(G'\) auch eine Strahldarstellung der Gruppe \(G\) (ggf. mit möglichen Zusatzbedingungen für die Superposition von Zuständen, also Superauswahlregeln). |
Was aber, wenn man die Zentralladungen nicht wegdefinieren kann? Dann gibt es Strahldarstellungen der Gruppe \(G'\), die nicht äquivalent zu einer unitären Darstellung von \(G'\) sind. Man kann dann aber in \[ [T(A_i), T(A_j)] = i \, f^k_{\,ij} \, T(A_k) + i \, C_{ij} \, 1 \] die Terme \( i \, C_{ij} \, 1 \) einfach in die Darstellung der Lie-Algebra integrieren, indem wir neue Operatoren hinzunehmen, die \(C_{ij}\) als Eigenwerte auf dem Hilbertraum besitzen. Für jede Zentralladung \(C_{ij}\) entsteht so ein weiterer Operator \(T_{neu}\) in der Darstellung der Lie-Algebra, der mit allen anderen Darstellungsoperatoren der bisherigen Generatoren vertauscht.
Nun kann man die bisherige Lie-Algebra so um neue Generatoren \(A_{neu}\) erweitern, dass die neuen Operatoren Darstellungsoperatoren von neuen Generatoren sind: \(T_{neu} = T(A_{neu})\). Mit Hilfe dieser erweiterten Lie-Algebra können wir dann die zugehörige einfach zusammenhängende Gruppe über die Exponentialabbildung konstruieren. Diese Gruppe ist gleichsam eine einfache Erweiterung der ursprünglichen Gruppe um neue Gruppenelemente und wird als Zentrale Erweiterung der Gruppe bezeichnet.
Die Darstellung der Lie-Algebra dieser neuen Gruppe enthält nun keine Zentralladungen mehr (denn diese sind ja nun Darstellungen der neuen Generatoren), so dass wir den obigen Satz wieder anwenden können und eine unitäre Darstellung dieser Gruppe erreichen können. Im allgemeinsten Fall kann man also Strahldarstellungen einer Lie-Gruppe \(G\) konstruieren, indem man die zentrale Erweiterung der universellen Überlagerungsgruppe aufsucht und deren unitäre Darstellungen konstruiert.
Oder aber man bleibt bei der universellen Überlagerungsgruppe und lebt mit der meist recht einfachen Phase in der fast-unitären Strahldarstellung dieser Gruppe. So habe ich in John F. Dawson: Quantum Mechanics: Fundamental Principles and Applications in Kapitel 4.4 auf S.45 den Satz gefunden: There seems to be no particular advantage in using this extended scheme (gemeint ist die zentrale Erweiterung der Galileigruppe). Wir werden uns das am Beispiel der Galileigruppe in einem späteren Kapitel noch genauer ansehen.
Damit sind wir nun gerüstet, um uns mit den Strahldarstellungen der beiden wichtigsten Gruppen zu befassen: Der Galileigruppe und der Poincarégruppe. Als Vorbereitung schauen wir uns dazu aber zunächst wichtige Untergruppen dieser beiden Gruppen an: die Raum-Zeit-Translationen und die Drehungen. Im nächsten Schritt können wir dann die nichtrelativistischen Boosts hinzunehmen und so zur Galileigruppe vorstoßen, oder aber über die relativistischen Boosts zur Poincarégruppe gelangen. Bei den Drehungen wird dabei die Überlagerungsgruppe der Drehgruppe ins Spiel kommen, und bei den nichtrelativistischen Boosts die zentrale Erweiterung der Gruppe.
© Jörg Resag, www.joerg-resag.de
last modified on 29 July 2023