Kommen wir nun zu einem anderen Objekt, das man auf Mannigfaltigkeiten definieren kann, und das ebenfalls etwas mit Richtungen zu tun hat: den Co-Tangentialvektoren, die auch Differentialformen oder 1-Formen genannt werden.
Co-Tangentialvektoren sind so etwas wie Gradienten von skalaren Funktionen, die auf einer Mannigfaltigkeit definiert sind. Stellen wir uns wieder eine zweidimensionale Fläche im dreidimensionalen Raum vor, sowie eine skalare Funktion \(\phi\), die in diesem Raum (und somit auch auf der Fläche) definiert ist.
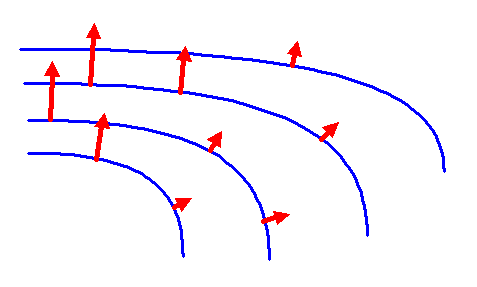
Der Gradient der Funktion \(\phi\) an einem Punkt \(p\) der Fläche ist dann in euklidischen Koordinaten gegeben durch den Vektor \[ \mathrm{grad} \, \phi = \begin{pmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{pmatrix} \] Dieser Vektor zeigt in die Richtung, in der \( \phi \) am stärksten ansteigt (siehe Bild unten).
Die Projektion dieses Vektors auf den Tangentialraum der Fläche wäre dann
ein Co-Tangentialvektor (alternativ kann man auch \(\phi\) so wählen, dass sie sich
nur tangential zur Fläche ändert).

Bleibt die Frage: Was unterscheidet einen Co-Tangentialvektor eigentlich von einem
Tangentialvektor? Anschaulich sind beide nach der obigen Konstruktion ja
Vektoren im dreidimensionalen Einbettungsraum, die tangential zur Fläche in \(p\) sind.
Die Antwort lautet: Es handelt sich um zwei Objekte mit verschiedenem mathematischen Ursprung:
Nur in euklidischen Koordinaten im Einbettungsraum sehen diese Objekte gleich aus.
Der Grund liegt darin, dass wir eine Metrik brauchen, um überhaupt von Längen und Winkeln auf der Mannigfaltigkeit reden zu können. Bei einer Einbettung im euklidischen Raum ist eine solche Metrik automatisch vorhanden. Diese Metrik verwenden wir in unserer Anschauung, um die Gradientenrichtung und die Richtung eines Tangentialvektors miteinander zu vergleichen. Ohne eine solche Metrik weiß man nicht, wie man eine Gradientenrichtung mit einer Tangentialvektorrichtung überhaupt in Beziehung setzen soll. Die Anschauung in den obigen Bildern, bei der die Tangentenrichtung senkrecht auf den Höhenlinien steht, beruht eben gerade auf der euklidischen Metrik. Auch die bekannte Formel für die Richtungsableitung im dreidimensionalen euklidischen Raum \[ \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} = (\mathrm{grad} \, \phi) \cdot \gamma'(0) \] setzt eine Metrik (ein Skalarprodukt \( \cdot \)) zwischen den dreidimensionalen Vektoren \( \mathrm{grad} \, \phi \) und dem Tangentialvektor \( \boldsymbol{\gamma}'(0)\) voraus. Erst dieses Skalarprodukt ermöglicht es uns, \( \mathrm{grad} \, \phi \) als einen Vektor analog zu \( \gamma'(0) \) anzusehen. Details dazu werden wir in einem späteren Kapitel noch genauer kennenlernen.
Wo der Unterschied zwischen Tangentialvektoren und Co-Tangentialvektoren liegt, wird deutlich, wenn wir uns wieder die Richtungsableitung der skalaren Funktion \(\phi\) in Richtung der Kurve \(\gamma\) in \(p = \gamma(0)\) ansehen, wobei wir die Koordinaten auf der Fläche mit \(x^{\mu}\) bezeichnen wollen (also nicht mit Koordinaten des Einbettungsraums verwechseln!). Wir gehen zunächst wieder von einer Einbettung aus, so dass wir direkt (vielleicht etwas lässig) schreiben dürfen: \[ \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} = \sum_{\mu} \, \frac{\partial \phi}{\partial x^{\mu}} \, \frac{d\gamma^{\mu}}{dt} \bigg|_{t = 0} \] Die präzise Schreibweise für die obige Formel (siehe vorheriges Kapitel) lautet übrigens: \[ \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} = \] \[ = \sum_{\mu} \, \frac{ \partial(\phi \circ f^{ -1})}{\partial x^{\mu}} \bigg|_{f(p)} \cdot \frac{d}{dt} (f \circ \gamma)^{\mu}(t) \bigg|_{t = 0} \] mit einer Karte (Koordinatensystem) \(f^\mu(p) = x^\mu |_p\) auf der Mannigfaltigkeit in einer Umgebung von \(p\), aber das ist doch oft etwas unhandlich. Wir schreiben daher die Koordinatenfunktion \(f\) nicht immer hin. Der Koordinatenindex \(\mu\) macht ja immer klar, dass sich der Ausdruck auf die Koordinatendarstellung bezieht.
Bei einem Koordinatenwechsel transformieren sich die Komponenten \[ u^\mu(p) := \frac{d\gamma^{\mu}}{dt} \bigg|_{t = 0} := \frac{d}{dt} (f \circ \gamma)^{\mu}(t) \bigg|_{t = 0} \] kontraviariant (hatten wir weiter im vorherigen Kapitel bereits definiert), d.h. es handelt sich dabei um die Komponenten eines Tangentialvektors.
Die Komponenten \[ \omega_\mu(p) := \frac{\partial \phi}{\partial x^{\mu}} := \frac{ \partial(\phi \circ f^{ -1})}{\partial x^{\mu}} \bigg|_{f(p)} \] dagegen müssen sich bei Koordinatenwechseln genau entgegengesetzt transformieren, d.h. kovariant (definieren wir etwas später noch genau), damit die Richtungsableitung insgesamt invariant bleibt. Wir schreiben den Koordinatenindex \(\mu\) hier entsprechend unten hin, um das entgegengesetzte Transformationsverhalten zu signalisieren.
Einen Co-Tangentialvektor könnten wir daher als abstraktes Objekt definieren, dessen Komponenten sich kovariant transformieren.
Würden wir im euklidischen Einbettungsraum krummlinige Koordinaten verwenden, so würde uns auch dort der Unterschied zwischen Tangentialvektoren und Co-Tangentialvektoren auffallen. Das merkt man spätestens, wenn man beispielsweise Geschwindigkeiten und Gradienten in Kugelkoordinaten verwenden muss. Jeder Physiker kennt das lästige Nachschlagen des Gradienten in Kugelkoordinaten, da er sich anders verhält als ein Geschwindigkeitsvektor. Auf einer gekrümmten Fläche bleibt einem aber nichts anderes übrig, als krummlinige Koordinaten zu verwenden. Daher ist hier der Unterschied zwischen Tangentenvektor und Co-Tangentenvektor wichtig!
Schauen wir uns nun an, wie das erwähnte abstrakte Objekt konkret aussehen kann, dessen Komponenten sich kovariant transformieren sollen. Dabei werden wir zunächst den Weg über konkrete Koordinaten gehen und Co-Tangentialvektoren als dual zu den Tangentialvektoren definieren, im Sinne des Dualraums, der aus der Linearen Algebra her bekannt ist. Dies ist der Weg, wie er in der theoretischen Physik gerne gewählt wird.
Weiter unten werden wir dann Co-Tangentialvektoren noch einmal koordinatenunabhängig einführen. Dabei lassen wir uns von der Idee leiten, dass Co-Tangentialvektoren etwas mit Gradienten zu tun haben. Die Verbindung zwischen beiden Wegen wird dabei ebenfalls klar werden.
Am Schluss wollen wir noch eine Definition erwähnen, wie sie in der abstrakten mathematischen Literatur gerne verwendet wird: die Definition über Äquivalenzklassen, ganz analog zu den Kurven-Äquivalenzklassen \( [\gamma]_{p}\) von oben, nur diesmal als Äquivalenzklassen von skalaren Funktionen \([\phi]_{p}\).
Aus der linearen Algebra kennt man zu jedem Vektorraum mit Basis \(e_{\mu}\) einen dazu dualen Co-Vektorräum mit Basis \(e^{\nu}\) und der Regel \[ e^{\nu} e_{\mu} = \delta^{\nu}_{\,\mu} \] Das Kroneckersymbol \( \delta^{\nu}_{\,\mu} \) ist gleich 1 für \(\mu = \nu\) und Null sonst.
Die Elemente des Co-Vektorraums sind dabei lineare Abbildungen (Linearformen), die jedem Vektor des Vektorraums eine reelle Zahl zuordnen. Insofern bedeutet \( e^{\nu} e_{\mu} \), dass die Basis-Linearform \(e^{\nu}\) auf den Basisvektor \(e_{\mu}\) angewendet wird. Vorsicht! Nicht mit dem Skalarprodukt für orthonormierte Basisvektoren verwechseln! Ein solches Skalarprodukt haben wir bisher nicht definiert, und es lässt sich allgemein auf Mannigfaltigkeiten so auch nicht definieren – der Metrik-Begriff liefert hier die geeignete Verallgemeinerung (siehe ein späteres Kapitel).
Die Regel \( e^{\nu} e_{\mu} = \delta^{\nu}_{\,\mu} \) erinnert stark an die Regel \[ \frac{\partial x^{\nu}}{\partial x^{\mu}} = \delta^{\nu}_{\,\mu} \] Tatsächlich ist diese Regel das geeignete Analogon auf Mannigfaltigkeiten, denn sie weist für die \(\mu\)- und \(\nu\)-Indizes das richtige Transformationsverhalten bei Koordinatenwechseln auf. Daher orientiert man sich in der Schreibweise im Folgenden auch an dieser Regel und definiert die Basisvektoren \[ dx^{\nu}|_{p} \] des Co-Tangentialraums als Linearformen auf den Basisvektoren \( \frac{\partial}{\partial x^{\mu}} \big|_p \) des Tangentialraums (haben wir im vorhergehenden Kapitel definiert) über die Regel \[ dx^{\nu}|_{p} \, \frac{\partial}{\partial x^{\mu}} \bigg|_p = \delta^{\nu}_{\,\mu} \] Die Schreibweise bedeutet, dass die Basis-Linearform \(dx^{\nu}|_{p}\) des Co-Tangentialraums auf den Basisvektor \( \frac{\partial}{\partial x^{\mu}} \big|_p \) des Tangentialraums angewendet wird (das \(p\) lassen wir in Zukunft auch oft weg).
Auf diese Weise umgehen wir das Problem, mit infinitesimalen Objekten hantieren zu müssen, und können stattdessen mit wohldefinierten mathematischen Begriffen arbeiten. Die dazugehörende Anschauung liegt aber in den infinitesimalen Längenelementen begründet – das merkt man spätestens dann, wenn man zu Integralen übergeht (siehe unten).
Übrigens eröffnet die sogenannte Nicht-Standard-Analysis durchaus die Möglichkeit, infinitesimale Objekte mathematisch sauber über Mengen zu definieren. Diese Objekte haben den Grenzwertprozess gleichsam bereits eingebaut (siehe Die Grenzen der Berechenbarkeit, Kapitel 3.1 Übernatürliche Zahlen ).
In vielen physikalisch orientierten Büchern ist man damit bereits weitgehend fertig:
|
Co-Tangentialraum als Dualraum zum Tangentialraum: Man definiert den Co-Tangentialraum \(T^{*}(p)\) als die Menge aller Linearformen auf dem Tangentialraum \(T(p)\), d.h. jedes Element \(\omega(p)\) des Co-Tangentialraums ist eine lineare Abbildung auf dem Tangentialraum, die jedem Tangentialvektor \(u(p)\) die reelle Zahl \( \omega(p) \, u(p) \) zuordnet. Weiter definiert man die Addition und Skalarmultiplikation im Co-Tangentialraum durch \[ (\omega(p) + \rho(p)) \, u(p) := \omega(p) \, u(p) + \rho(p) \, u(p) \] \[ (c \, \omega(p)) \, u(p) := c \, (\omega(p) \, u(p)) \] (mit reellen Zahlen \(c\) und Co-Tangentialvektoren (Linearformen) \(\omega\) und \(\rho\)) und macht so aus ihm einen Vektorraum, der dieselbe Dimension wie der Tangentialraum und wie die Mannigfaltigkeit (d.h. wie der Bildraum der Koordinatenfunktionen) hat. Jedes Element \(\omega\) des Co-Tangentialraums kann man nun nach einer Basis \(dx^{\nu}|_{p}\) entwickeln, d.h. \[ \omega(p) = \sum_{\nu} \, \omega_{\nu}(p) \, dx^{\nu}|_{p} \] wobei die Basis \(dx^{\nu}|_{p}\) durch die Eigenschaft \[ dx^{\nu}|_{p} \, \frac{\partial}{\partial x^{\mu}} \bigg|_p = \delta^{\nu}_{\,\mu} \] festgelegt ist. Die Basis wird also wie beim Tangentialraum auch durch eine Koordinatenfunktion \(f\) in einer Umgebung von \(p\) auf der Mannigfaltigkeit festgelegt. |
Diese Vorgehensweise leistet genau das Gewünschte, denn damit
ist
\[
\omega(p) \, u(p) =
\sum_{\mu} \, \omega_{\mu}(p) \, u^{\mu}(p)
\]
Damit der ganze Ausdruck koordinatenunabhängig ist, müssen sich
die koordinatenabhängigen Komponenten
\( \omega_{\mu}(p) \) und \( u^{\mu}(p) \)
bei Koordinatenwechseln genau entgegengesetzt zueinander transformieren (siehe genauer weiter unten).
Diesen Unterschied im Transformationsverhalten kennzeichnen wir durch
die Indexstellung oben bzw. unten.
Schauen wir uns nun noch einmal genauer an, was das Ganze mit Gradienten zu tun hat. Dazu starten wir wieder mit einer differenzierbaren skalaren Funktion \(\phi\), die in einer Umgebung von \(p\) auf der Mannigfaltigkeit definiert ist, sowie einer Kurve \(\gamma(t)\), die bei \(t=0\) durch \(p\) geht. Wir definieren nun die Abbildung \(d\phi(p)\) wie folgt:
|
\[ d\phi(p) \, u(p) := u(p) \, \phi = \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} \] |
Hintergrund: Oben hatten wir anhand von \[ \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} = \sum_{\mu} \, \frac{\partial \phi}{\partial x^{\mu}} \, \frac{d\gamma^{\mu}}{dt} \bigg|_{t = 0} \] gesehen, wie Tangentenvektor und Gradient zusammen eine Richtungsableitung ergeben. Im vorherigen Kapitel hatten wir die Richtungsableitung dazu verwendet, den Tangentenvektor \(u(p)\) als Abbildung auf \(\phi\) zu definieren. Wir machen es nun umgekehrt und verwenden die Richtungsableitung in \(p\), um das Gradienten-Analogon \(d\phi(p)\) als Abbildung auf \(u(p)\) zu definieren.
\(d\phi(p)\) ist also eine Abbildung, die einem Tangentialvektor \(u(p)\) eine reelle Zahl zuordnet (nämlich die Richtungsableitung von \(\phi\) im Punkt \(p\) in Richtung der durchlaufenden Kurve \(\gamma(t)\)). Man kann leicht zeigen, dass \(d\phi(p)\) eine Linearform ist, also ein Element des Co-Tangentialraums. Wir können analog zu oben daher auch \[ \omega(p) := d\phi(p) \] schreiben.
Machen wir uns den Unterschied zwischen den beiden Verwendungen der obigen Gleichung klar:
Die Rollen von \(\phi\) und \(\gamma\) sind also in beiden Fällen gleichsam vertauscht.
Vielleicht ist das folgende Bild noch ganz nützlich: In dem Ausdruck \( \phi(\gamma(t)) \) wird einer reellen Zahl \(t\) über die Kurve \(\gamma\) ein Punkt auf der Mannigfaltigkeit \(M\) zugeordnet, und diesem wird anschließend über die skalare Funktion \(\phi\) wieder eine reelle Zahl zugeordnet: \[ \mathbb{R} \overset{\gamma}{\longrightarrow} M \overset{\phi}{\longrightarrow} \mathbb{R} \] \[ \quad \quad \quad t \longrightarrow \gamma(t) \longrightarrow \phi(\gamma(t)) \] Betrachtet man nun die Veränderung \[ \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} \] so hängt diese von der Veränderung von \(\gamma\) in \(t = 0\) sowie von der Veränderung von \(\phi\) in \(\gamma(0) = p\) ab.
Die Veränderung (die Richtung bzw. Geschwindigkeit) der Kurve \(\gamma\) ergibt eine Abbildung \(u(p)\) (den Tangentialvektor), und die Veränderung (das Gefälle, also der Gradient) der skalaren Funktion \(\phi\) ergibt eine Abbildung \(d\phi\) (den Co-Tangentialvektor).
Die obigen Definitionen ermöglichen es uns nun, konkrete Ausdrücke für die Basisvektoren \( dx^{\nu}|_{p} \) zu ermitteln, so wie wir das auch bei den Basisvektoren \( \frac{\partial}{\partial x^{\mu}} \big|_{p} \) gemacht haben. Dazu brauchen wir einfach nur die entsprechende Rechnung aus dem vorherigen Kapitel noch einmal zu wiederholen: \[ d\phi(p) \, u(p) := u(p) \phi = \] \[ = \frac{d}{dt} \phi(\gamma(t)) \big|_{t = 0} = \] \[ = \frac{d}{dt} (\phi \circ f^{ -1} \circ f \circ \gamma) (t) \big|_{t = 0} = \] \[ = \sum_{\nu} \, \frac{ \partial(\phi \circ f^{ -1})}{\partial x^{\nu}} \bigg|_{f(p)} \cdot \frac{d}{dt} (f \circ \gamma)^{\nu}(t) \bigg|_{t = 0} \] (den Index haben wir hier in \(\nu\) umbenannt). Nun müssen wir nur noch die Terme geeignet neu interpretieren: Wir lassen den linken Term \( \frac{ \partial(\phi \circ f^{ -1})}{\partial x^{\nu}} \big|_{f(p)} \) als reelle Zahl einfach unverändert stehen und verwenden den zweiten Term, um allgemein die Linearform \( dx^{\nu}|_{p} \) zu definieren: \[ dx^{\nu}|_{p} \, u(p) := \frac{d}{dt} (f \circ \gamma)^{\nu}(t) \bigg|_{t = 0} = u^{\nu}(p) \] Diese Definition sorgt dann automatisch für die Gültigkeit der Regel \[ dx^{\nu}|_{p} \, \frac{\partial}{\partial x^{\mu}} \bigg|_p = \delta^{\nu}_{\,\mu} \] Insgesamt haben wir damit: \[ d\phi(p) = \sum_{\nu} \, \frac{ \partial(\phi \circ f^{ -1})}{\partial x^{\nu}} \bigg|_{f(p)} \, dx^{\nu}|_{p} \] was in der Physik gerne abgekürzt geschrieben wird als \[ d\phi = \sum_{\nu} \, \frac{\partial \phi}{\partial x^{\nu}} \, dx^{\nu} \] Es gilt ganz allgemein, dass wir für festes \(p\) immer eine geeignete skalare Funktion \(\phi\) finden können, so dass sich jeder Co-Tangentialvektor \(\omega(p)\) als \[ \omega(p) = d\phi(p) \] schreiben lässt. Wir müssen für \(\phi\) ja nur fordern, dass in \(p\) bei vorgegebenen Koordinaten gilt: \[ \omega_{\nu}(p) = \frac{ \partial(\phi \circ f^{ -1})}{\partial x^{\nu}} \bigg|_{f(p)} \] Doch Vorsicht! Wenn wir zu Co-Tangential-Vektorfeldern übergehen (ein Co-Tangential-Vektorfeld \(\omega\) ist einfach eine Abbildung, die jedem Punkt \(p\) einen Co-Tangentialvektor \(\omega(p)\) zuordnet), und analog \( \omega = d\phi \) schreiben wollen, so geht das nicht mehr für beliebige \(\omega\).
Analog lässt sich auch im dreidimensionalen euklidischen Raum nicht jedes (Co-)Vektorfeld als Gradient einer skalaren Funktion (eines Potentials) schreiben – das geht nur punktweise. Zur Erinnerung: Nur wenn die Rotation des Vektorfeldes gleich Null ist, kann man es als Gradient schreiben. Ein Analogon dazu lässt sich auch für Co-Tangential-Vektorfelder (Differentialformen) formulieren.
Die obige Formel für \(\omega_{\nu}(p)\) erlaubt es uns, das Transformationsverhalten bei Koordinatenwechseln noch einmal explizit nachzuweisen. Die \(f\)-Koordinaten bezeichnen wir analog zu oben mit \(x = (x^\mu)\) und die g-Koordinaten mit \(y = (y^\nu)\), d.h. \[ (f \circ g^{ -1})(y) = x \] Die Umrechnung ergibt: \[ \omega_{\mu}(p) = \frac{ \partial(\phi \circ f^{ -1})}{\partial x^{\nu}} \bigg|_{f(p)} = \] \[ = \frac{ \partial(\phi \circ g^{ -1} \circ g \circ f^{ -1})}{\partial x^{\nu}} \bigg|_{f(p)} = \] \[ = \sum_{\sigma} \, \frac{ \partial(\phi \circ g^{ -1})}{\partial y^{\sigma}} \bigg|_{g(p)} \, \frac{ \partial( g \circ f^{ -1})^{\sigma}}{\partial x^{\mu}} \bigg|_{f(p)} = \] \[ =: \sum_{\sigma} \, \rho_{\sigma}(p) \, \frac{ \partial(g \circ f^{ -1})^{\sigma}}{\partial x^{\mu}} \bigg|_{f(p)} \] Dabei sind die \(\rho_{\sigma}(p)\) die Komponenten von \(\omega\) in den neuen \(y\)-Koordinaten, und \[ \frac{ \partial(g \circ f^{ -1})^{\sigma}}{\partial x^{\mu}} \bigg|_{f(p)} \] ist die Jacobimatrix der Koordinatenumrechnungsfunktion \( g \circ f^{ -1} \). Vergleichen wir dies mit dem Transformationsverhalten der Tangentenvektor-Komponenten \[ u^{\mu}(p) =: \] \[ =: \sum_{\nu} \, \frac{\partial (f \circ g^{ -1})^{\mu}}{\partial y^{\nu}} \bigg|_{g(p)} \, v^{\nu}(p) \] (siehe das vorherige Kapitel), so sehen wir, dass das Transformationsverhalten genau entgegengesetzt ist. Damit ist sichergestellt, dass \[ \omega(p) \, u(p) = \] \[ = \sum_{\mu} \, \omega_{\mu}(p) \, u^{\mu}(p) = \] \[ = \sum_{\mu} \, \rho_{\mu}(p) \, v^{\mu}(p) \] koordinatenunabhängig ist. Die beiden Umrechnungs-Jacobi-Matrizen sind nämlich invers zueinander (beachte dabei: \(\mathrm{id}^{\mu}(g(p)) = y^{\mu}\)) : \[ \sum_{\mu} \, \frac{\partial (g \circ f^{ -1})^{\sigma}}{\partial x^{\mu}} \bigg|_{f(p)} \, \frac{\partial (f \circ g^{ -1})^{\mu}} {\partial y^{\nu}} \bigg|_{g(p)} = \] \[ = \frac{\partial (g \circ f^{ -1} \circ f \circ g^{ -1})^{\mu}}{\partial y^{\nu}} \bigg|_{g(p)} = \] \[ \frac{\partial (\mathrm{id})^{\mu}}{\partial y^{\nu}} \bigg|_{g(p)} = \] \[ = \frac{\partial y^{\mu}}{\partial y^{\nu}} = \delta^{\mu}_{\,\nu} \] Wem diese Schreibweise zu unhandlich ist, dem sei die etwas unsaubere, aber sehr intuitive Physikerschreibweise ans Herz gelegt: \[ \omega_{\mu}(p) = \sum_{\sigma} \, \rho_{\sigma}(p) \, \frac{\partial y^{\sigma}}{\partial x^{\mu}} \] was zusammen mit \[ u^{\mu}(p) = \sum_{\nu} \, \frac{\partial x^{\mu}}{\partial y^{\nu}} \, v^{\nu}(p) \] einfach ergibt: \[ \omega(p) \, u(p) = \sum_{\mu} \, \omega_{\mu}(p) \, u^{\mu}(p) = \] \[ = \sum_{\mu} \, \sum_{\sigma} \, \sum_{\nu} \, \rho_{\sigma}(p) \, \frac{\partial y^{\sigma}}{\partial x^{\mu}} \, \frac{\partial x^{\mu}}{\partial y^{\nu}} \, v^{\nu}(p) = \] \[ = \sum_{\sigma} \, \sum_{\nu} \, \rho_{\sigma}(p) \, \frac{\partial y^{\sigma}}{\partial y^{\nu}} \, v^{\nu}(p) = \] \[ = \sum_{\sigma} \, \sum_{\nu} \, \rho_{\sigma}(p) \, \delta^{\sigma}_{\,\nu} \, v^{\nu}(p) = \] \[ = \sum_{\nu} \, \rho_{\nu}(p) \, v^{\nu}(p) \]
Die obige Definition benötigt einen Tangentialraum, um den dazu dualen Co-Tangentialraum als Raum der Linearformen auf dem Tangentialraum zu definieren. Man kann den Co-Tangentialraum allerdings auch definieren, ohne auf den Tangentialraum zurückgreifen zu müssen. Diese Art der Definition ist sehr allgemein und lässt sich am einfachsten auf andere Bereiche der Mathematik (z.B. die algebraische Geometrie) übertragen. Man geht in diesem Fall sogar gerne von dieser allgemeinen Definition des Co-Tangentialraums aus und definiert dann den Tangentialraum als Raum der Linearformen auf dem Co-Tangentialraum (also genau umgekehrt).
Die Idee ist analog zur Definition von Tangentenvektoren als Äquivalenzklassen \( [\gamma]_{p} \) zueinander tangentialer Kurven im Punkt \(p\) (siehe vorheriges Kapitel). Diesmal allerdings verwenden wir Äquivalenzklassen \( [\phi]_{p} \) skalarer Funktionen mit gleicher Veränderung (Gradient) in \(p\). Bei \( [\gamma]_{p} \) hatte wir also Kurven mit gleicher Veränderung in \( t = 0 \), bei \( [\phi]_{p} \) dagegen haben wir skalare Funktionen mit gleicher Veränderung in \(p\).
Schauen wir uns diese allgemeine Definition einmal genauer an: Wir geben einen Punkt \(p\) der Mannigfaltigkeit vor, zu dem wir den Co-Tangentialraum definieren wollen, und betrachten die Menge (nennen wir sie \(I(p)\) ) aller skalaren differenzierbaren Funktionen \(\phi\), die jedem Punkt der Mannigfaltigkeit eine reelle Zahl zuordnen, und die im vorgegebenen Punkt \(p\) eine Nullstelle haben: \[ \phi(p) = 0 \] (dieser Punkt ist eigentlich relativ unwichtig – letztlich kommte es auf die Veränderung von \(\phi\) in \(p\) an, sodass wir den Wert einfach auf Null festlegen können).
Wir wollen die Menge \(I(p)\) dieser skalaren Funktionen nun in Teilmengen (Äquivalenzklassen) aufteilen. Dabei sollen zwei Funktionen \(\phi_{1}\) und \(\phi_{2}\) in derselben Äquivalenzklasse liegen, wenn sich ihre Differenz \( \phi_{1}(q) - \phi_{2}(q) \) in einem ggf. anderen Punkt \(q\) schreiben lässt als Produkt zweier Funktionen \(\phi_{3}(q)\) und \(\phi_{4}(q)\) aus \(I(p)\) (die jeweils also auch in \(q = p\) eine Nullstelle haben): \[ \phi_{1}(q) - \phi_{2}(q) = \phi_{3}(q) \, \phi_{4}(q) \] Schauen wir uns an, was das bedeutet. Dazu bilden wir die erste Ableitung. Diese kann man über Koordinatensysteme definieren – wir verzichten hier darauf und schreiben etwas unpräzise (der Strich bedeutet die Ableitung in irgendeine Richtung): \[ \phi_{1}'(q) - \phi_{2}'(q) = \] \[ = \phi_{3}'(q) \, \phi_{4}(q) + \phi_{3}(q) \, \phi_{4}'(q) \] Setzen wir hier \(q = p\) ein und verwenden \(\phi_{3}(p) = \phi_{3}(p) = 0\), so ergibt sich daraus \[ \phi_{1}'(q) - \phi_{2}'(q) = 0 \] Das bedeutet:
|
Wir betrachten zwei skalare Funktionen aus \(I(p)\) (d.h. mit Nullstelle in \(p\)) als gleichwertig (äquivalent), wenn sie sich im Punkt \(p\) nur um das Produkt zweier Funktionen aus \(I(p)\) unterscheiden. Das bedeutet, dass gleichwertige Funktionen aus \(I(p)\) dieselbe erste Ableitung besitzen. Aus den jeweis zueinander gleichwertigen Funktionen bilden wir entsprechende Äquivalenzklassen \[ [\phi]_{p} \] d.h. wie fassen die zueinander gleichwertigen Funktionen in Mengen zusammen. Die Äquivalenzklassen repräsentieren Funktionen mit derselben Veränderung in \(p\). |
In der mathematischen Literatur wird dies oft so ausgedrückt:
Die Teilmenge der Funktionen aus \(I(p)\), die sich als Produkt zweier anderer Funktionen aus \(I(p)\) schreiben lassen, bezeichnet man als \(I^{2}(p)\). Funktionen in \(I(p)\) haben in \(p\) also eine Nullstelle, während bei Funktionen aus \(I^{2}(p)\) auch die erste Ableitung (definiert über entsprechende Koordinaten) in \(p\) gleich Null ist.
Nun bildet man den Quotientenraum \[ I(p) / I^{2}(p) \] Die Elemente dieses Raums sind die oben definierten Äquivalenzklassen, also die Mengen zueinander gleichwertiger Funktionen. Der Begriff gleichwertig ist dabei über \(I^{2}(p)\) definiert: zwei Funktionen aus \(I(p)\) sind gleichwertig, wenn ihre Differenz eine Funktion in \(I^{2}(p)\) ist.
Der Co-Tangentialraum in \(p\) ist nun gerade definiert als dieser Quotientenraum \( I(p) / I^{2}(p) \). Anschaulich (und etwas lässig formuliert) bedeutet das: Der Co-Tangentialraum dagegen besteht aus allen möglichen ersten Ableitungen (Gradienten) skalarer Funktionen in \(p\).
Wie kann man nun die Definition des Co-Tangentenvektors über die Äquivalenzklasse \([\phi]_{p}\) in die Definition über die Linearform \(d\phi(p)\) von weiter oben übersetzen?
Wir haben es durch die Schreibweise \(d\phi(p)\) im Grunde bereits vorweggenommen, denn wir können eine Abbildung \(d\) definieren, die diese Übersetzung vornimmt: Jeder Funktion \(\phi\) aus \([\phi]_{p}\) ordnet \(d\) eindeutig diejenige Linearform \(d\phi(p)\) zu, die weiter oben über \[ d\phi(p) \, u(p) := u(p) \, \phi = \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} \] definiert ist.
Man kann für ein Co-Tangentenvektorfeld (Differentialform oder 1-Form) \[ \omega = \sum_{\nu} \, \omega_{\nu} \, dx^{\nu} \] das Integral über eine Kurve \(\gamma(t)\) auf der Mannigfaltigkeit \(M\) wie folgt definieren (dabei läuft der Kurvenparameter \(t\) von \(a\) nach \(b\), was wir als \(t \in T \) schreiben, \(\gamma(T)\) ist die Menge aller entsprechenden Kurvenpunkte in \(M\) und \( f \) liefert die Koordinaten in diesem Kurvenbereich): \[ \int_{\gamma(T)} \omega := \] \[ = \int_{a}^{b} \, \omega(\gamma(t)) \, u(\gamma(t)) \, dt = \] \[ = \int_{a}^{b} \, \sum_{\nu} \, \omega_{\nu}(\gamma(t)) \, \frac{d}{dt} (f \circ \gamma)^{\nu}(t) \, dt \] oder in Physiker-Kurzschreibweise \[ \int \omega = \int \, \sum_{\nu} \,\omega_{\nu} \, dx^{\nu} = \] \[ = \int \, \sum_{\nu} \, \omega_{\nu} \, \frac{dx^{\nu}}{dt} \, dt \] Wichtig ist dabei, dass dieses Integral koordinatenunabhängig ist, also nicht von \(f\) abhängt. Das wird durch das kovariante Transformationsverhalten der \(\omega_{\nu}\) garantiert. Die Basisvektoren \(dx^{\nu}\) dagegen transformieren sich bei Koordinatenwechsel genau wie \((f \circ \gamma)^{\nu}(t)\). Deshalb ist die obige Definition überhaupt erst möglich!
Weiterhin hängt das obige Integral nicht von der Parametrisierung der Kurve ab, d.h. sein Wert ändert sich bei (orientierungserhaltenden) Umparametrisierungen der Kurve nicht.
Beispiele für solche Kurvenintegrale sind aus der Physik wohlbekannt, z.B. das Wegintegral des Elektrischen Feldes \( \int \boldsymbol{E \, ds}\). Dabei kann man \( \boldsymbol{E \, ds} \) durchaus als Co-Tangentenvektor auffassen, was sich beispielsweise in Kugelkoordinaten sofort bemerkbar macht. Mehr dazu siehe in einem späteren Kapitel über Differentialformen.
Sowohl der Tangentialvektorraum \(T(p)\) als auch der Co-Tangentialvektorraum \(T^{*}(p)\) im Punkt \(p\) sind n-dimensionale reelle Vektorräume. Man kann also immer Abbildungen (Isomorphien) zwischen diesen beiden Räumen definieren und so gewisse Tangentialvektoren und Co-Tangentialvektoren einander zuordnen. Aber: Es gibt bisher keine solche Zuordnung, die sich von selbst anbieten würde und die ohne weitere Zutaten eine Sonderrolle genießen würde.
Ein Beispiel:
Man könnte auf die Idee kommen, jedem Tangentialvektor
\[
u(p) = \sum_{\mu} \, u^{\mu}(p) \frac{\partial}{\partial x^{\mu}} \bigg|_{p}
\]
einen Co-Tangentialvektor
\[
\omega(p) = \sum_{\mu} \, \omega_{\mu}(p) \, dx^{\mu}|_{p}
\]
mit identischen Komponenten zuzuordnen:
\[
\omega_{\mu}(p) := u^{\mu}(p)
\]
Ganz nach dem Motto: zwei Vektoren mit gleichen Komponenten sind gleich.
Aber sobald man das Koordinatensystem wechselt, sind diese Komponenten i.a. schon nicht
mehr gleich, denn kovariante und kontravariante Komponenten transformieren sich
entgegengesetzt.
Erst eine Metrik wird es uns später erlauben, bestimmte Zuordnungen zwischen den beiden Vektorräumen als bevorzugt zu kennzeichnen und so aus einem Tangentialvektor einen Co-Tangentialvektor machen zu können. Die euklidische Metrik ist dabei ein Spezialfall: Hier sind tatsächlich die Komponenten von Tangential- und Co-Tangentialvektoren in euklidischen (geradlinig-senkrechten) Koordinaten gleich! Deshalb unterscheidet man im euklidischen Raum auch meist nicht zwischen beiden Vektorsorten – ein Umstand, der bei der Verwendung krummliniger Koordinaten (Beispielsweise Kugelkoordinaten) schnell für Verwirrung sorgt, denn hier wird der Unterschied wichtig!
Wie wir oben gesehen haben, kann man jeden Co-Tangentialvektor \(\omega(p)\) lokal durch das Änderungsverhalten einer skalaren Funktion \(\phi\) beschreiben: \( \omega(p) = d\phi(p) \) mit. \[ \omega(p) \, u(p) = d\phi(p) \, u(p) := \] \[ = u(p) \, \phi = \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} \] Das Änderungsverhalten von \(\phi\) in einer kleinen Umgebung von \(p\) können wir durch Höhenlinien bzw. Höhenflächen anschaulich darstellen, also in einer n-dimensionalen Mannigfaltigkeit \(M\) durch (n-1)-dimensionale Flächen, auf denen \(\phi\) konstant ist – wir werden zur Vereinfachung auch die (n-1)-dimensionalen Höhenflächen als Höhenlinien bezeichnen. Diese Höhenlinien nahe bei \(p\) könnten also auch eine Veranschaulichung des Co-Tangentialvektors \( \omega(p) = d\phi(p) \) liefern.
Wenn das so ist, müssten wir aus den Höhenlinien von \(\phi\) nahe bei \(p\) auch den Wert von \( \omega(p) \, u(p) = d\phi(p) \, u(p) \) ableiten können. Und tatsächlich geht das ganz einfach:
Wenn wir in Richtung des Tangentialvektors \(u(p)\) (also in Richtung der entsprechenden Kurve \(\gamma\))
ein winzig kleines Stück vorangehen, so werden wir umso mehr Höhenlinien überschreiten,
je schneller sich \(\phi\) in dieser Richtung ändert.
Dabei zählen wir Höhenlinien positiv, wenn es bergauf geht, ansonsten negativ.
Der Wert von \( \omega(p) \, u(p) \) entspricht also in diesem Bild
der Zahl der Höhenlinien (mit Vorzeichen), die man in \(u(p)\)-Richtung überschreitet.
So ergibt sich anschaulich für \( \omega(p) \, u(p) \)
die Richtungsableitung von \(\phi\) im Punkt \(p\) in \(u(p)\)-Richtung.
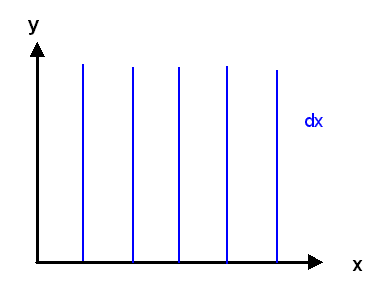
Siehe auch Dan Piponi:
On the Visualisation of Differential Forms.
Nun gilt diese Vorstellung zunächst nur lokal, also nur in einer kleinen (sogar infinitesimalen)
Umgebung von \(p\). Wir können uns aber vorstellen, dass wir die Mannigfaltigkeit näherungsweise
mit sehr vielen sehr kleinen Umgebungen gleichsam pflastern und in jeder dieser Umgebungen
den Co-Tangentialvektor \(\omega\) durch Höhenlinien einer Funktion \(\phi\) darstellen.
Dabei ist \(\phi\) jeweils nur in dieser winzigen Umgebung definiert, und es kann sein,
dass wir in jeder Umgebung eine andere Funktion \(\phi\) brauchen.
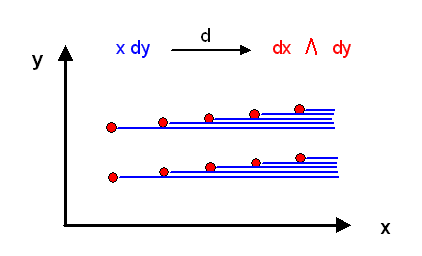
Schauen wir uns ein einfaches Beispiel an: Die Mannigfaltigkeit \(M\) ist die zweidimensionale reelle Ebene \( \mathbb{R}^{2} \) mit den beiden Koordinaten \(x\) und \(y\), und der Co-Tangentialvektor \(\omega\) ist gegeben durch \[ \omega = x \, dy \] Wir wählen nun einen beliebigen Punkt \( p = (a,b) \) aus und betrachten die Umgebung dieses Punktes. In dieser Umgebung definieren wir die skalare Funktion \(\phi\) als \[ \phi(x,y) = a \, y \] so dass \[ d\phi(x,y) = a \, dy \] ist. Damit haben wir erreicht, dass im Punkt \( p = (a,b) \) die gewünschte Beziehung \( \omega(a,b) = d\phi(a,b) \) gilt.
Schauen wir uns die Höhenlinien von \( \phi(x,y) = a \, y \) nahe bei \( p = (a,b) \) an: \(\phi\) steigt nur in \(y\)-Richtung an, und zwar mit der Steigung \(a\). Der Anstieg wird also in Umgebungen von Punkten weiter rechts (also mit größerem \(a\)) immer steiler, aber gleichzeitig erfolgt der Anstieg immer in \(y\)-Richtung. So etwas ist nur mit lokal definierten Funktionen \(\phi\) erreichbar, nicht aber mit einer einzigen Funktion \(\phi\).
Die Höhenlinien liegen also parallel zur x-Achse, und ihre Dichte ist proportional zur Steigung \(a\). Je weiter rechts der Punkt \( p = (a,b) \) liegt, umso dichter sind die Höhenlinien der dort lokal definierten Funktion \(\phi\).
Wenn wir uns nun die gesamte Ebene mit kleinen Umgebungen gepflastert vorstellen und überall die Höhenlinien der entsprechenden \(\phi\)-Funktion einzeichnen, so erhalten wir folgendes Bild:
Je weiter rechts eine Umgebung liegt, umso mehr waagrechte Höhenlinien enthält sie,
weil das lokal definierte \(\phi\) stärker in \(y\)-Richtung ansteigt.
An den Grenzen der Umgebungen kommen also von links nach rechts immer neue Höhenlinien dazu.
Wenn wir die Umgebungen unendlich klein werden lassen, so entspricht dies einer bestimmten
Entstehungsdichte von nach rechts fortlaufenden Höhenlinien.
Diese Entstehung von neuen Höhenlinien ist die Ursache dafür,
dass wir nicht die Höhenlinien einer einzigen
Funktion \(\phi\) in der ganzen Ebene verwenden können.
Siehe auch Dan Piponi:
On the Visualisation of Differential Forms.
Das Höhenlinien-Bild lässt sich auch gut auf Kurvenintegrale
\[
\int_{\gamma(T)} \omega =
\int_{a}^{b} \, \omega(\gamma(t)) \, u(\gamma(t)) \, dt
\]
von Co-Tangentialvektoren anwenden. Bei einem solchen Kurvenintegral werden einfach die
auf dem Weg durchstoßenen Höhenlinien (ggf. mit negativem Vorzeichen beim Abstieg)
aufsummiert.
Wir haben oben versucht, uns von der Einbettung einer Mannigfaltigkeit in einen höherdimensionalen reellen euklidischen Raum zu lösen und die Begriffe einbettungsfrei zu definieren. Dabei mussten wir in Kauf nehmen, dass Begriffe wie der Tangentenvektor nicht mehr direkt als Ableitung einer Kurve \( \gamma'(0) \) definiert werden können, sondern etwas umständlich als Äquivalenzklassen oder als Abbildungen (Richtungsableitungen) eingeführt werden müssen.
Bleibt die Frage, ob man nicht doch die Mannigfaltigkeiten hätte einbetten können und sich so die abstrakte Einführung von Begriffen hätte sparen können. Das ist tatsächlich der Fall, denn es gilt:
|
Einbettungssatz von Hassler Whitney (1944): Man kann jede (einfach-) differenzierbare Mannigfaltigkeit \(M\) der Dimension \(n\) differenzierbar im \(2n\)-dimensionalen euklidischen Raum \(\mathbb{R}^{2n}\) einbetten (ohne Selbstüberschneidungen). |
Differenzierbar einbetten heißt,
dass es eine differenzierbare injektive Abbildung von \(M\) nach \(\mathbb{R}^{2n}\)
gibt. Die Injektivität ist dabei gleichbedeutend mit dem Verbot von
Selbstüberschneidungen. Dabei kann es durchaus vorkommen,
dass weniger als \(2n\) Dimensionen gebraucht werden.
Es gibt aber viele Fälle, in denen eine Dimension mehr (also \(n+1\) Dimemsionen) nicht
ausreichen. Ein Beispiel dazu werden wir etwas weiter unten gleich kennenlernen.
Es lässt sich also jede differenzierbare Mannigfaltigkeit als glatter Unterraum des euklidischen Raums ansehen. Man hätte dies dazu verwenden können, um die abstrakte Einführung von Tangentialvektoren etc. zu vermeiden. Ein Tangentialvektor wäre dann einfach der Vektor \(\gamma'(0)\) im Einbettungsraum, und ein Co-Tangentialvektor wäre ein Gradient.
Man zahlt jedoch einen Preis: Viele differenzierbare Mannigfaltigkeiten besitzen keine in natürlicher Weise gegebene Einbettung, denn sie sind ohne eine solche Einbettung definiert. Es gibt dann oft mehrere Einbettungs-Möglichkeiten, die man teilweise erst aufwendig konstruieren muss. Zudem führt jede Einbettung zu zusätzlichen Strukturen auf der Mannigfaltigkeit, insbesondere zu einer Metrik (wie wir noch sehen werden). Diese neuen Strukturen haben aber mit der Struktur der ursprünglichen Mannigfaltigkeit wenig zu tun und stören eher, als dass sie nützen. Daher ist es sehr nützlich, auf eine Einbettung verzichten zu können und stattdessen mit der Mannigfaltigkeit so arbeiten zu können, wie sie definiert wurde. Dabei helfen die abstrakt definierten Begriffe wie Tangential- und Cotangentialvektoren enorm.
Ein Beispiel ist die sogenannte projektive Ebene, die ein gutes Modell für die Geometrie des perspektivischen Sehens ergibt. Die projektive Ebene entsteht aus \(\mathbb{R}^{3}\) (ohne den Nullvektor), indem man alle zueinander kollinearen Vektoren in Äquivalenzklassen zusammenfasst und die Menge dieser Klassen betrachtet. Kollinear bedeutet, dass die Vektoren parallel zueinander gerichtet (aber nicht unbedingt gleich lang) sind, wobei sie aber durchaus entgegengesetzt orientiert sein dürfen, d.h. \( \boldsymbol{x} \) uns \( -\boldsymbol{x} \) sind auch kollinear. Die projektive Ebene ist also der Raum der Richtungen im dreidimensionalen Raum oder auch der Raum der Geraden durch den Ursprung im dreidimensionalen Raum. Diese Geraden sind gleichsam die Sichtlinien vom Auge des Betrachters hinaus in die dreidimensionale Welt.
Die projektive Ebene ist eine zweidimensionale differenzierbare Mannigfaltigkeit. Man kann sie sich veranschaulichen, indem man die Geradendurchstoßpunkte an der Einheits-Kugeloberfläche als Punkte der Mannigfaltigkeit ansieht, wobei aber die beiden jeweils gegenüberliegenden Durchstoßpunkte nur einen Punkt der projektiven Ebene repräsentieren, da sie zur selben Geraden gehören. Die projektive Ebene entspricht also der zweidimensionalen Kugeloberfläche, wobei man jeweils die gegenüberliegenden Punkte miteinander identifizieren muss.
Man könnte statt der ganzen Kugeloberfläche nur die halbe Kugeloberfläche
nehmen, so dass jede Ursprungsgerade nur einen Durchstoßpunkt ergibt.
Erreicht ein solcher Durchstoßpunkt den Rand der Halbkugeloberfläche und verlässt sie
(verschwindet also am Rand),
so taucht der Punkt an der gegenüberliegenden Seite am Rand wieder auf, da die Gerade
nun dort ihren Durchstoßpunkt hat. Lässt man auf diese Weise z.B. ein Dreieck
über den Rand hinaus auf die gegenüberliegende Seite wandern, so stellt man fest, dass
das Dreieck nun spiegelsymmetrisch zu vorher ist.
Man sagt daher, die projektive Ebene ist eine nicht orientierbare Mannigfaltigkeit,
ähnlich wie das Möbiusband (das allerdings einen Rand besitzt).
Man kann die projektive Ebene auf verschiedene Weise
im vierdimensionalen Raum als zweidimensionale
Fläche einbetten. Leider kann man sich das nicht gut veranschaulichen.
Im dreidimensionalen Raum (wo unsere Anschauung funktioniert) kann man
ebenfalls Einbettungen finden, die allerdings nicht überschneidungsfrei (selbst-durchdringungsfrei) sind.
Man kann dazu beispielsweise vom Möbiusband ausgehen und versuchen, dessen Kante (ja, es gibt nur eine!)
mit der Kante einer Scheibe zu verkleben (was ohne Selbstdurchdringungen nicht geht – außerdem gibt
es für das Verkleben verschiedene Möglichkeiten!).
Beispiele für Einbettungen mit Selbstdurchdringungen im dreidimensionalen Raum
sind die Römer-Fläche
(auch Steiner-Fläche oder engl. roman surface genannt)
und die Boy'sche Fläche (engl. Boy's surface).
Jede dieser Einbettungen ergibt eine andere Möglichkeit, eine Metrik (also Längen und Winkel) auf der projektiven Ebene zu definieren. Da sich jedoch in der projektiven Ebene keine natürliche Möglichkeit für die Definition einer Metrik mit Längen und Winkeln anbietet, haben diese Einbettungs-Metriken keinen großen Nutzen (Anmerkung: es macht allerdings Sinn, einen Abstandsbegriff einzuführen und so einen metrischen Raum zu konstruieren!). Normalerweise ist es daher besser, die projektive Ebene ohne die möglichen Einbettungen darzustellen und zu untersuchen. Gut, dass man dann auf Tangentialvektoren und Co-Tangentialvektoren trotzdem nicht zu verzichten braucht.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 15 September 2023