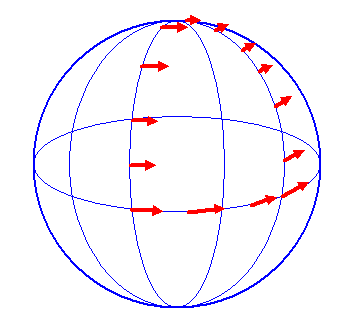
Ausgehend von einem gegebenen affinen Zusammenhang (kovariante Ableitung, Paralleltransport und Christoffelsymbole sind also definiert) wollen wir in diesem Kapitel den Begriff der Krümmung auf einer Mannigfaltigkeit zu definieren. Ausgangspunkt ist dabei die folgende anschauliche Beobachtung:
Das folgende Bild, das wir bereits aus Kapitel 6:
Kovariante Ableitung und Paralleltransport kennen,
veranschaulicht diesen Zusammenhang am Beispiel einer Kugeloberfläche:

Wichtig ist, dass wir auf diese Weise die Krümmung vollkommen unabhängig von
einer Einbettung definieren können. Würden wir auf der Erde auf diese Weise einen
Paralleltransport durchführen, so könnten wir die Krümmung der Erdoberfläche erkennen,
ohne in den Weltraum hinausfliegen zu müssen! Übrigens: wir gehen davon aus, dass
unsere Kurve keine Löcher in der Mannigfaltigkeit (wie z.B. in einem Donut – einem Torus)
umrundet, d.h. die Kurve soll topologisch trivial sein.
Konkret werden wir die Krümmung in einem Punkt \(p\) mit Hilfe einer infinitesimale geschlossene Kurve definieren, die in dem Punkt p startet und wieder endet. Beispielsweise kann man ein kleines Viereck nehmen, wobei wir hier nicht voraussetzen wollen, dass es sich um ein Parallelogramm handelt (mit einem Parallelogramm befassen wir uns weiter unten).
Ein solches Viereck mit einem Punkt \(p\) als Eckpunkt lässt sich über eine differenzierbare Abbildung \(g\) von \(\mathbb{R}^{2}\) auf die Mannigfaltigkeit \(M\) darstellen, d.h. \(g(t, t')\) ist für jedes Wertepaar ein Punkt auf der Mannigfaltigkeit.
Die vier Punkte des Vierecks sollen nun durch \[ p = g(0, 0) \] \[ q = g(\epsilon, 0) \] \[ r = g(\epsilon, \epsilon') \] \[ s = g(0, \epsilon') \] gegeben sein. Die vier Kurven, die die Seiten des Rechtecks darstellen, sind entsprechend gegeben durch \[ g(t, 0) \] \[ g(0, t') \] \[ g(t, \epsilon') \] \[ g(\epsilon, t') \] mit t zwischen \(0\) und \(\epsilon\) und \(t'\) zwischen \(0\) und \(\epsilon'\).
Dabei wollen wir nicht verlangen, dass diese Kurven geodätische Linien sein müssen – die Seiten des Vierecks müssen also nicht unbedingt gerade sein (Parallelität hatten wir ebenfalls nicht vorausgesetzt).
Ein infinitesimales Viereck erhalten wir dann im Grenzübergang unendlich kleiner Werte für \(\epsilon\) und \(\epsilon'\).
Wir wollen die beiden Richtungsvektoren in \(p\), die in Richtung der Viereck-Seiten \( g(t, 0) \) und \( g(0, t') \) zeigen, mit \(u(p)\) und \(v(p)\) bezeichnen, d.h. \[ u(p) \, \phi = \frac{d}{dt} \phi(g(t, 0)) \bigg|_{t = 0} \] \[ v(p) \, \phi = \frac{d}{dt'} \phi(g(0, t')) \bigg|_{t' = 0} \] mit einer skalaren Funktion \(\phi\) auf der Mannigfaltigkeit.
Man kann nun einen Tangentialvektor \(w(p)\) entlang der vier Seiten dieses Rechtecks im Kreis von \(p\) über \(q\) und \(r\) nach \(s\) und schließlich zurück nach \(p\) paralleltransportieren und diesen Vektor \(w'(p)\) nach seiner Rundreise mit dem ursprünglichen \(w(p)\) vergleichen. Die etwas mühsame Rechnung findet man beispielsweise in Matt Visser: Math 464: Notes on differential geometry. Wir wollen sie hier überspringen und nur das Ergebnis angeben. In zweiter Ordnung der Parameter \(\epsilon\) und \(\epsilon'\) ergibt sich für die Komponenten von \(w\) (bezogen auf Koordinaten \(x = (x^\mu) \) mit Koordinatenfunktion \(f\)): \[ (w'(p) - w(p))^{\mu} = \] \[ = \sum_{\nu\rho\sigma} \, R^{\mu}_{\,\nu\rho\sigma} \, w^{\nu}(p) \, u^{\rho}(p) \, v^{\sigma}(p) \, \epsilon \, \epsilon' + \, ... \] mit \[ R^{\mu}_{\,\nu\rho\sigma} = \frac{\partial \Gamma^{ \mu}_{\sigma\nu}}{\partial x^{\rho}} - \frac{\partial \Gamma^{ \mu}_{\rho\nu}}{\partial x^{\sigma}} + \] \[ + \sum_{\alpha} \, \left( \Gamma^{ \mu}_{\rho\alpha} \, \Gamma^{ \alpha}_{\sigma\nu} - \Gamma^{ \mu}_{\sigma\alpha} \, \Gamma^{ \alpha}_{\rho\nu} \right) \] Dabei stellen die drei Punkte ... wie im letzten Kapitel Terme höherer Ordnung in \(\epsilon\) und \(\epsilon'\) dar, die im Grenzfall sehr kleiner \(\epsilon\) und \(\epsilon'\) (also einer infinitesimalen Rundreise) keine Rolle mehr spielen.
Wir bezeichnen \( R^{\mu}_{\,\nu\rho\sigma} \) als die Komponenten des Riemann'schen Krümmungstensors. Dieser Tensor stellt die Krümmung einer Mannigfaltigkeit im Punkt \(p\) mathematisch dar.

Quelle:
Wikimedia Commons File:Georg Friedrich Bernhard Riemann.jpeg
Nun ist die obige Formel bisweilen etwas unübersichtlich. Man kann sie mit Hilfe von Differentialformen in eine übersichtlichere Form bringen. Dazu verwenden wir die in Kapitel 6: Kovariante Ableitung und Paralleltransport definierte Matrix \( \Theta \), deren Elemente die folgenden Co-Tangentialvektoren sind (das Argument \(p\) lassen wir zur Vereinfachung weg): \[ \Theta^{ \rho}_{\,\mu} := \sum_{\nu} \, \Gamma^{ \rho}_{\nu\mu} \, dx^{\nu} \] Man kann nun ein sogenanntes äußeres Produkt \( \wedge \) (auch Dachprodukt oder antisymmetrisches Tensorprodukt genannt) zwischen zwei Co-Tangentialvektoren wie folgt definieren:
|
äußeres Produkt von Co-Tangentialvektoren: \[ [ dx^{\mu} \wedge dx^{\nu} ] (u, v) := u^{\mu} \, v^{\nu} - u^{\nu} \, v^{\mu} \] (die Argumente \(p\) haben wir weggelassen). Das äußere Produkt \( dx^{\mu} \wedge dx^{\nu} \) ist also eine antisymmetrische bilineare Abbildung auf dem Raum der Tangentialvektoren, deren Ergebniswert eine reelle Zahl ist. Man bezeichnet \( dx^{\mu} \wedge dx^{\nu} \) (bzw. Linearkombinationen davon) auch als 2-Formen. Aus der Definition geht unmittelbar hervor, dass \[ dx^{\mu} \wedge dx^{\nu} = - dx^{\nu} \wedge dx^{\mu} \] ist. |
Wir wollen nun das äußere Produkt dazu verwenden, um die Matrix
\( \Theta \wedge \Theta \) zu definieren:
\[
(\Theta \wedge \Theta)^{\mu}_{\,\nu}
:=
\]
\[
:= \sum_{\alpha} \,
\Theta^{\mu}_{\,\alpha} \wedge \Theta^{\alpha}_{\,\nu}
=
\]
\[
=
\sum_{\alpha} \,
\left[ \sum_{\rho} \Gamma^{\mu}_{\rho\alpha} \, dx^{\rho} \right]
\wedge
\left[ \sum_{\sigma} \Gamma^{\alpha}_{\sigma\nu} \, dx^{\sigma} \right]
=
\]
\[
=
\sum_{\alpha\rho\sigma} \,
\Gamma^{ \mu}_{\rho\alpha} \,
\Gamma^{ \alpha}_{\sigma\nu} \,
dx^{\rho} \wedge dx^{\sigma}
\]
so dass
\[
(\Theta \wedge \Theta)^{\mu}_{\,\nu} (u, v)
=
\]
\[
=
\sum_{\alpha\rho\sigma} \,
\Gamma^{ \mu}_{\rho\alpha} \,
\Gamma^{ \alpha}_{\sigma\nu} \,
[ dx^{\rho} \wedge dx^{\sigma} ] (u, v)
=
\]
\[
=
\sum_{\alpha\rho\sigma} \, \left(
\Gamma^{ \mu}_{\rho\alpha} \,
\Gamma^{ \alpha}_{\sigma\nu}
-
\Gamma^{ \mu}_{\sigma\alpha} \,
\Gamma^{ \alpha}_{\rho\nu} \right)
u^{ \rho} v^{\sigma}
\]
ergibt. Das ist genau der Summenterm im Krümmungstensor!
Um auch die Ableitungsterme der Christoffelsymbole im Krümmungstensor umschreiben zu können, definieren wir die äußere Ableitung eines Co-Tangentialvektors wie folgt:
|
äußeres Ableitung von Co-Tangentialvektoren: Die äußere Ableitung eines Co-Tangentialvektors \[ \omega = \sum_{\mu} \, \omega_{\mu} \, dx^{\mu} \] (siehe Kapitel 5: Co-Tangentialräume und Differentialformen, wobei wir das Argument \(p\) zur Vereinfachung wieder weglassen) definieren wir als \[ d\omega := \sum_{\mu} d\omega_{\mu} \wedge dx^{\mu} \] Dabei ist \[ d\omega_{\mu} = \sum_{\nu} \, \frac{\partial \omega_{\mu}}{\partial x^{\nu}} \, dx^{\nu} \] (die genaue Definition und Schreibweise findet man in Kapitel 5: Co-Tangentialräume und Differentialformen bei der Definition von \(d\phi(p)\), wobei hier die skalare Funktion \(\omega_{\mu}\) an die Stelle von \(\phi\) tritt). Insgesamt haben wir also \[ d\omega = \sum_{\mu\nu} \, \frac{\partial \omega_{\mu}}{\partial x^{\nu}} \, dx^{\nu} \wedge dx^{\mu} \]
|
Dies können wir nun auf die Matrix \(\Theta\) anwenden:
\[
(d\Theta)^{\mu}_{\,\nu} :=
d(\Theta^{\mu}_{\, \nu}) =
\]
\[
=
\sum_{\rho} \, d\Gamma^{\mu}_{\rho\nu} \, dx^{ \rho}
=
\]
\[
=
\sum_{\rho\sigma} \,
\frac{\partial \Gamma^{\mu}_{\rho\nu}}{\partial x^{\sigma}}
\, dx^{\sigma} \wedge dx^{\rho}
\]
so dass
\[
(d\Theta)^{\mu}_{\,\nu} (u, v) =
\]
\[
=
\sum_{\rho\sigma} \,
\frac{\partial \Gamma^{\mu}_{\rho\nu}}{\partial x^{\sigma}}
\, [ dx^{\sigma} \wedge dx^{ \rho} ] (u, v)
=
\]
\[
=
\sum_{\rho\sigma} \,
\left( \frac{\partial \Gamma^{\mu}_{\sigma\nu}}{\partial dx^{\rho}}
-
\frac{\partial \Gamma^{\mu}_{\rho\nu}}{\partial x^{\sigma}} \right)
\, u^{\rho} \, v^{ \sigma}
\]
Das ist genau der Ableitungsterm im Krümmungstensor.
Es bietet sich daher an, die folgende Krümmungs-2-Form-Matrix \(R\)
wie folgt zu definieren:
|
Cartans Krümmungs-2-Form-Matrix \(R\): Wir definieren Cartans Krümmungs-2-Form-Matrix \(R\) durch \[ R := d\Theta + \Theta \wedge \Theta \] mit \[ \Theta^{ \rho}_{\,\mu} := \sum_{\nu} \, \Gamma^{ \rho}_{\nu\mu} \, dx^{\nu} \] so dass die Matrixelemente von \(R\) gegeben sind durch die 2-Formen \[ R^{\mu}_{\,\nu} = (d\Theta)^{\mu}_{\,\nu} + (\Theta \wedge \Theta)^{\mu}_{\,\nu} = \] \[ = \sum_{\rho\sigma} \, \bigg( \frac{\partial \Gamma^{\mu}_{\sigma\nu}}{\partial x^{\rho}} + \sum_{\alpha} \, \Gamma^{\mu}_{\rho\alpha} \, \Gamma^{\alpha}_{\sigma\nu} \bigg) \, dx^{\rho} \wedge dx^{\sigma} \] Dann ist die Veränderung eines Tangentialvektors \(w\) beim Kreis-Paralleltransport um das Viereck gegeben durch \[ w' - w = R(u, v) \, w \, \epsilon \, \epsilon' + \, ... \] d.h. \[ (w'(p) - w(p))^{\mu} = \] \[ = [R(u, v) w]^{\mu} \, \epsilon \, \epsilon' + \, ... = \] \[ = \sum_{\nu} \, R^{\mu}_{\,\nu} (u, v) \, w^{\nu}(p) \, \epsilon \, \epsilon' + \, ... = \] \[ = \sum_{\,\nu\rho\sigma} \, R^{\mu}_{\,\nu\rho\sigma} \, w^{\nu}(p) \, u^{\rho}(p) \, v^{\sigma}(p) \, \epsilon \, \epsilon' + \, ... \] mit \[ R^{\mu}_{\,\nu\rho\sigma} = \frac{\partial \Gamma^{ \mu}_{\sigma\nu}}{\partial x^{\rho}} - \frac{\partial \Gamma^{ \mu}_{\rho\nu}}{\partial x^{\sigma}} + \] \[ + \sum_{\alpha} \, \left( \Gamma^{ \mu}_{\rho\alpha} \, \Gamma^{ \alpha}_{\sigma\nu} - \Gamma^{ \mu}_{\sigma\alpha} \, \Gamma^{ \alpha}_{\rho\nu} \right) \] Wie man sieht, ist \( R^{\mu}_{\,\nu\rho\sigma} \) antisymmetrisch in \(\rho\) und \(\sigma\). Eine weitere Schreibweise ist \[ R = \frac{1}{2} \,\sum_{\rho\sigma} \, R_{\rho\sigma} \, dx^{ \rho} \wedge dx^{\sigma} \] In dieser Schreibweise ist für jede Kombination von \(\rho\) und \(\sigma\) der Koeffizient \( R_{\rho\sigma} \) eine Matrix mit Matrixelementen \( R^{\mu}_{\,\nu\rho\sigma} \). |
Die elegante
Darstellung
\[
R := d\Theta + \Theta \wedge \Theta
\]
geht auf den französischen Mathematiker
Élie Cartan
(1869 - 1951) zurück.
Die Darstellung besitzt ein enges Analogon in der Eichtheorie, in der \(\Theta\) durch die
Eichpotentialform \(A\) und die Krümmung \(R\) durch den Feldstärketensor \(F\) ersetzt wird
(siehe auch
Quantenfeldtheorie und Eichfelder, Kapitel 6: Eichtheorien ).
Für die Definition der Krümmungsmatrix \(R\) haben wir bestimmte Koordinaten \(x\) verwendet, d.h. die konkrete Form der Matrix \(R\) ist koordinatenabhängig. Weiter unten werden wir den Riemann'schen Krümmungstensor (den wir ebenfalls mit \(R\) bezeichnen werden, um nicht zu viele Bezeichnungen zu verwenden) noch koordinatenunabhängig einführen. Für den Moment merken wir uns:
Fragen wir uns nach dem Transformationsverhalten von \(R\) bei Koordinatenwechseln. In Kapitel 6: Kovariante Ableitung und Paralleltransport hatten wir gesehen: Geht man nun von Koordinaten \(x\) zu Koordinaten \(x'\) über mit der Jacobi-Matrix \[ J^{\lambda}_{\,\mu} := \frac{\partial x^{\lambda}}{\partial x'^{\mu}} \] (wir verwenden hier die etwas unsaubere, aber sehr praktische und intuitive Physiker-Schreibweise), so gilt die Matrixgleichung \[ \Theta' = J^{-1} \, \Theta \, J + J^{-1} \, dJ \] Dabei ist \(\Theta'\) die Matrix bezüglich der neuen Koordinaten \(x'\). Die äußere Ableitung \(dJ\) kennen wir bereits von der Definition von \(d\phi\) aus Kapitel 5 Co-Tangentialräume und Differentialformen – sie gilt hier für jedes Matrixelement von \(J\). Eine kleine Rechnung (die wir hier überspringen) zeigt: \[ R' = J^{-1} \, R \, J \] Das Transformationsverhalten von \(R\) ist also sehr einfach. Insbesondere folgt aus \( R = 0 \), dass auch \( R' = 0 \) ist. Bei \( \Theta \) ist das nicht so (das muss auch so sein, denn schließlich kann man bei flachen Mannigfaltigkeiten immer von karthesischen Koordinaten (d.h. \( \Theta = 0 \)) zu krummlinigen Koordinaten (d.h. \( \Theta' \ne 0 \)) übergehen).
Bei der obigen Diskussion haben wir die Details der Rechnung, die den Zusammenhang zwischen den Komponenten \( R^{\mu}_{\,\nu\rho\sigma} \) des Riemannschen Krümmungstensors und den Christoffelsymbolen herstellt, einfach übersprungen. Wir wissen nur: Wenn man einen Vektor \(w\) entlang eines infinitesimalen Vierecks im Kreis paralleltransportiert, so kann man den Unterschied des neuen Vektors \(w'\) zu \(w\) mit Hilfe der Paralleltransport-Differentialgleichung ausrechnen und erhält die oben angegebene Formel für \( R^{\mu}_{\,\nu\rho\sigma} \).
Später haben wir diese Formel eleganter als \[ R = d\Theta + \Theta \wedge \Theta \] geschrieben. Der Grund, warum wir \(R\) als Krümmung bezeichnet haben, liegt dabei in der folgenden Anschauung: \(w\) und \(w'\) sind nur dann verschieden, wenn eine Krümmung vorliegt. Also muss \(R\) ein Maß für die Krümmung sein.
Cartans Darstellung ermöglicht es uns nun, eine Motivation dafür finden, warum diese Formel für \(R\) tatsächlich etwas mit einer Krümmung zu tun haben soll. Genauer wollen wir folgendes zumindest plausibel machen:
Genauer:
Wenn \( R = 0 \) ist (und die Torsion ebenfalls Null ist), so kann man durch eine Koordinatentransformation von \(x\) nach \(x'\) erreichen, dass \(\Theta'\) (also die Christoffelsymbole) in den neuen Koordinaten gleich Null sind. Man sagt dann, der Zusammenhang \(\Theta\) ist affin-flach.
Die Basisvektoren \( \frac{\partial}{\partial x'^{ \mu}} \) verändern sich damit anschaulich nicht von Punkt zu Punkt (vgl. die Definition der Christoffelsymbole bei einer Einbettung), d.h. \(x'\) sind karthesische Koordinaten auf der Mannigfaltigkeit.
Anmerkung:
Bei allgemeinen affinen Zusammenhängen \(\Theta\) mit nicht-verschwindender Torsion
gibt es flache Zusammenhänge (d.h. \(R = 0\) ), die nicht affin-flach sind.
Beginnen wir also mit dem krümmungsfreien Fall \[ R = d\Theta + \Theta \wedge \Theta = 0 \] Eine Lösung für \( \Theta \) lautet \[ \Theta = G^{-1} \, dG \] mit einer invertierbaren reellen Matrix \(G\).
Erfüllt dieses \Theta die geforderte Gleichung? Überprüfen wir es: \[ d \Theta = \] \[ = d (G^{-1} \, dG) = \] \[ = dG^{-1} \wedge dG = \] \[ = (dG^{-1}) \, G \, G^{-1} \wedge dG = \] \[ = (dG^{-1}) \, G \wedge G^{-1} \, dG = \] \[ = - G^{-1} \, dG \wedge G^{-1} \, dG = \] \[ = - \Theta \wedge \Theta \] d.h. der Ansatz \( \Theta = G^{-1} \, dG \) erfüllt \( R = 0 \). Dabei haben wir verwendet, dass \( d d G = 0 \) ist wegen der Antisymmetrie des Dachproduktes und der Vertauschbarkeit der partiellen Ableitungen. Weiter haben wir verwendet, dass die Matrixelemente von \(G\) reelle Zahlen sind, so dass \(G\) mit \(\wedge\) vertauscht. Und schließlich folgt aus \( 0 = d (G^{-1} \, G) \)\( = (dG^{-1}) \, G + G^{-1} \, dG \) die Beziehung \( (dG^{-1}) \, G = - G^{-1} \, dG \), was wir am Schluss verwendet haben.
Umgekehrt stellt sich natürlich die Frage: Ist \( \Theta = G^{-1} \, dG \) auch die allgemeinste Lösung für \(R = 0\) ? An dieser Stelle bin ich mir etwas unsicher. Nach Matt Visser: Math 464: Notes on differential geometry, Kapitel 3.10.3 Theorem 12) gilt \( R = 0 \) genau dann, wenn es ein Koordinatensystem gibt mit \[ \Gamma^{\rho}_{\nu\mu} = \frac{\partial D^{\rho}_{\,\mu}}{\partial x^{\nu}} \] (bei Matt Visser sind die Christoffelsymbole übrigens gerade mit vertauschten Indices definiert). Dabei sind \( D^{ \rho}_{\,\mu} \) die Matrixelemente einer Diagonalmatrix \(D\) (nicht mit der kovarianten Ableitung verwechseln!). Mit \[ \Theta^{\rho}_{\,\mu} = \sum_{\nu} \, \Gamma^{\rho}_{\nu\mu} \, dx^{\nu} = \] \[ = \sum_{\nu} \frac{\partial D^{\rho}_{\,\mu}}{\partial x^{\nu}} \, dx^{\nu} = d D^{\rho}_{\,\mu} \] können wir dies einfach schreiben als \[ \Theta = dD \] (man sieht, wie praktisch Cartans Schreibweise ist!). Dabei ist auch \(\Theta\) eine Diagonalmatrix. Diese Form hat \(\Theta\) gilt allerdings nur in einem ganz bestimmten Koordinatensystem. Unter welchen Voraussetzungen man durch eine Koordinatentransformation auf die Form \( \Theta = G^{-1} \, dG \) kommt, habe ich – ehrlich gesagt – nicht ausprobiert.
Kann man nun für \( \Theta = G^{-1} \, dG \) neue Koordinaten \(x'\) finden, so dass \( \Theta' = 0 \) ist? Versuchen wir es: \[ 0 = \Theta' = \] \[ = J^{-1} \, \Theta \, J + J^{-1} \, dJ = \] \[ = J^{-1} \, G^{-1} \, (dG) \, J + J^{-1} \, dJ = \] \[ = (GJ)^{-1} \, [ d(GJ) - G \, dJ ] + J^{-1} \, dJ = \] \[ = (GJ)^{-1} \, d(GJ) - (GJ)^{-1} \, G \, dJ + J^{-1} \, dJ = \] \[ = (GJ)^{-1} \, d(GJ) - J^{-1} \, dJ + J^{-1} \, dJ = \] \[ = (GJ)^{-1} \, d(GJ) \] Wir können also die Koordinatentransformation so wählen, dass für die entsprechende Jacobimatrix \(J\) gilt: \( G J = 1 \) und somit \(d(GJ) = 0\), d.h. \(J\) ist gerade die zu \(G\) inverse Matrix.
In Matt Visser: Math 464: Notes on differential geometry findet man zur Beziehung von Krümmung und affinen Zusammenhang eine ganze Reihe von Aussagen, die wir hier ohne Beweis einfach auflisten wollen:
|
Krümmung und Integrabilität: Wenn überall auf der Mannigfaltigkeit \( R = 0 \) ist, so ist der affine Zusammenhang integrabel, d.h. in jedem kontrahierbaren Bereich der Mannigfaltigkeit ist der Paralleltransport wegunabhängig – und umgekehrt. Dabei ist ein Bereich der Mannigfaltigkeit kontrahierbar, wenn sich jede geschlossene Kurve (Schleife) stetig in dieser Region zu einem Punkt zusammenziehen lässt. Statt kontrahierbar wird auch oft der Begriff einfach zusammenhängend verwendet.
Anmerkungen:
|
Unsere geometrische Überlegung zu Beginn dieses Kapitels liefert
im Grunde bereits den Beweis der Aussage, dass \( R = 0 \) gleichwertig zu
einem integrablen affinen Zusammenhang ist, denn ein Paralleltransport
entlang einer geschlossenen Kurve misst ja gerade die Wegabhängigkeit
des Paralleltransportes. Der Schritt von infinitesimalen Kurven zu endlichen Kurven
ist dabei nicht schwierig, denn eine endliche geschlossene Kurve kann man schrittweise in immer
kleinere geschlossene Kurven zerlegen (so geht man beispielsweise auch in der dreidimensionalen
Analysis beim Zusammenhang zwischen der Rotation eines Vektorfeldes und Wegintegralen
über geschlossene Kurven vor – Stichwort Satz von Stokes).
Man kann die Aussage auch auf ganz andere Art beweisen, indem man den Integrationssatz von Frobenius über bestimmte Differentialgleichungen verwendet (siehe wieder Matt Visser: Math 464: Notes on differential geometry). Dabei drückt man die Wegunabhängigkeit des Paralleltransports direkt durch die Differenzialgleichung für ein Parallelfeld längs einer Kurve aus. Schauen wir uns das genauer an:
Die Differenzialgleichung für ein Parallelfeld längs einer Kurve lautet (siehe Kapitel 6: Kovariante Ableitung und Paralleltransport): \[ \frac{d}{dt'} u^{\rho}(\gamma(t')) \bigg|_{t' = t} \, + \] \[ + \sum_{\mu\nu} \, u^{\mu}(\gamma(t)) \, \Gamma^{ \rho}_{\nu\mu}(\gamma(t)) \, v^{\nu}(\gamma(t)) = 0 \] Dabei sind \( v^{\nu}(\gamma(t)) \) die vorgegebenen Koeffizienten des zur Kurve \(\gamma(t)\) gehörenden Tangentialvektors, und \[ u(\gamma(t)) = \sum_{\mu} \, u^{\mu}(\gamma(t)) \frac{\partial}{\partial x^{\mu}} \bigg|_{\gamma(t)} \] ist ein Parallelfeld längs der vorgegebenen Kurve \(\gamma\).
Wir können den ersten Term noch etwas umschreiben (siehe Kapitel 4: Tangentialräume und Vektorfelder): \[ \frac{d}{dt'} u^{\rho}(\gamma(t')) \bigg|_{t' = t} = v(\gamma(t)) \, u^{\rho} = \] \[ = \sum_{\nu} \, v^{\nu}(\gamma(t)) \, \frac{\partial}{\partial x^{\nu}} \bigg|_{\gamma(t)} u^{\rho} \] so dass wir die Differenzialgleichung schreiben können als: \[ \sum_{\nu} \, \bigg[ \frac{\partial}{\partial x^{\nu}} \bigg|_{\gamma(t)} u^{\rho} + \] \[ + \sum_{\mu} \, u^{\mu}(\gamma(t)) \, \Gamma^{ \rho}_{\nu\mu}(\gamma(t)) \bigg] \, v^{\nu}(\gamma(t)) = 0 \] Nun soll der Paralleltransport integrabel sein, d.h. die konkrete Form der Kurve darf keine Rolle mehr spielen. Die obige Gleichung muss für alle Kurven richtig sein, also auch für alle Kurven-Tangentialvektoren \(v(\gamma(t))\), und für jede Kurve dasselbe parallele Vektorfeld \(u\) ergeben.
Wir können daher die obige Gleichung als eine Matrixgleichung für den Spaltenvektor \(v\) auffassen, die für jedes \(v\) richtig sein muss, so dass wir \(v\) weglassen können und das folgende Gleichungssystem verlangen dürfen (die Argumente wie \(\gamma(t)\) lassen sir hier weg): \[ \frac{\partial u^{\rho}}{\partial x^{\nu}} + \sum_{\mu} \, u^{\mu} \, \Gamma^{ \rho}_{\nu\mu} = 0 \] wobei wir \(u^{\rho}\) direkt als eine Funktion der Koordinaten \(x\) verstehen wollen (so vermeiden wir das lästige Einfügen der Koordinatenfunktion \(f\)).
Dieses Differenzialgleichungssystem ist gleichwertig zu der Forderung, dass der Zusammenhang integrabel sein soll! Dabei sind die Differenzialgleichungen spezielle Exemplare aus der Klasse der Differenzialgleichungen vom Frobenius-Mayer-Typ. Nach dem Integrationssatz von Frobenius ist dieses Gleichungssystem genau dann lösbar, wenn die Integrabilitätsbedingung \[ \frac{\partial \Gamma^{\mu}_{\sigma\nu}}{\partial x^{\rho}} - \frac{\partial \Gamma^{\mu}_{\rho\nu}}{\partial x^{\sigma}} + \] \[ + \sum_{\alpha} \bigg( \Gamma^{ \mu}_{\rho\alpha} \, \Gamma^{ \alpha}_{\sigma\nu} - \Gamma^{ \mu}_{\sigma\alpha} \, \Gamma^{ \alpha}_{\rho\nu} \bigg) = 0 \] erfüllt ist. Dies sind aber gerade die Komponenten des Riemannschen Krümmungstensors, d.h. die Integrabilitätsbedingung lautet einfach \( R = 0 \).
Die obige Definition des Riemannschen Krümmungstensors bezieht sich auf vorgegebene Koordinaten. Das ändert sich auch durch Cartans kompakte Schreibweise nicht. Es ist jedoch (analog zur Torsion im vorhergehenden Kapitel) oft nützlich, eine koordinatenunabhängige Formulierung zu haben. Wir wollen daher versuchen, eine solche Formulierung zu finden.
Im Riemannschen Krümmungstensor treten Produkte sowie Ableitungen von Christoffelsymbolen auf. Solche Terme erhält man, wenn man zwei kovariante Ableitungen nacheinander ausführt, also beispielsweise Terme wie \( D_{u} D_{v} w \) betrachtet. Wegen der Antisymmetrie von \(R\) bezüglich \(u\) und \(v\) (bzw. den entsprechenden Indizes \(\rho\) und \(\sigma\) in unseren Formeln ganz oben) ist es sinnvoll, daraus den antisymmetrischen Ausdruck \[ D_{u} D_{v} w - D_{v} D_{u} w \] zu bilden. Schreibt man diesen Ausdruck explizit in Komponenten aus, so stellt man jedoch fest, dass man noch Terme übrig behält. Diese lassen sich zum Ausdruck \[ D_{[u, v]} \, w \] zusammenfassen, wobei \( [u, v] \) die Lieklammer aus dem letzten Kapitel (über Torsion) ist.
Wir wollen die etwas mühsame Rechnung hier überspringen und direkt das Endergebnis angeben:
|
Koordinatenfreie Darstellung des Riemannschen Krümmungstensors: \[ R(u,v) = D_{u} D_{v} - D_{v} D_{u} - D_{[u, v]} \] |
(Hinweis: in vielen Fällen ist \( [u, v] = 0 \),
beispeilsweise für \( u = \frac{\partial}{\partial x^{\mu}} \)
und \( v = \frac{\partial}{\partial x^{\nu}} \)).
Dabei ist \(R(u,v)\) hier nicht als Matrix zu lesen, sondern
als Tensor auf den Tangentialvektoren, d.h.
\[
R(u,v) \, w :=
\]
\[ = \sum_{\mu} \,
[R(u, v) \, w]^{\mu} \, \frac{\partial}{\partial x^{\mu}}
=
\]
\[
=
\sum_{\mu\nu} \, R^{\mu}_{\,\nu}(u, v) \, w^{\nu}(p)
\, \frac{\partial}{\partial x^{\mu}}
=
\]
\[
=
\sum_{\mu\nu\rho\sigma} \,
R^{\mu}_{\,\nu\rho\sigma} \,
w^{\nu}(p) \, u^{\rho}(p) \, v^{\sigma}(p)
\, \frac{\partial}{\partial x^{\mu}}
\]
Hierbei verwenden wir die Schreibweise \( R(u,v) \, w \) in doppeltem Sinn:
Auf der linken Seite des ersten Gleichheitszeichens
wirkt der Tensor \(R(u,v)\) auf den Tangentialvektor \(w\).
Auf der rechten Seite des ersten Gleichheitszeichens
ist \(R\) eine 2-Form im Sinne Cartans, die auf die
Tangentialvektoren \(u\) und \(v\) angewendet eine Matrix
mit Matrixelementen \( R^{\mu}_{\,\nu}(u, v) \) ergibt, die auf den
Spaltenvektor \(w\) angewendet wird (so wie weiter oben beschrieben).
Es ist interessant, den Ausdruck \[ R(u,v) = D_{u} D_{v} - D_{v} D_{u} - D_{[u, v]} \] für den Krümmungstensor mit dem Ausdruck für die Torsion aus dem letzten Kapitel zu vergleichen: \[ T(u, v) = D_{u} v - D_{v} u - [u, v] \] Zur Erinnerung: die Torsion \(T(u, v)\) ist ein Tangential-Vektorfeld. Die Torsion kann man daher als Vektorfeld auf skalare Funktionen anwenden, beispielsweise auf Koordinatenfunktionen (in diesem Fall liefert die Torsion die Lücke in infinitesimalen Parallelogrammen, siehe vorheriges Kapitel).
Um aus der Torsion den Krümmungstensor zu machen, muss man nun einfach aus jedem der Vektoren \(u\), \(v\) und \([u, v]\) die zugehörige kovariante Ableitung machen. Den Krümmungstensor kann man nun auf Tangentialvektorfelder anwenden und so bestimmen, wie stark sich ein Vektor \(w\) ändert, wenn er infinitesimal im Viereck (gegeben durch \(u\) und \(v\)) im Kreis paralleltransportiert wird. Auf diese Weise erhält man ein Maß für die Krümmung der Mannigfaltigkeit.
Sowohl die Torsion als auch der Krümmungstensor enthalten jeweils Terme, wie sie den Seiten eines infinitesimalen Parallelogramms mit geschlossener Lücke entsprechen (siehe letztes Kapitel): Man läuft ein kleines Stück in \(v\)-Richtung, dann ein kleines Stück in \(u\)-Richtung, springt über die Lücke (geht also ein kleines Stück in \( - [u, v] \) -Richtung) und geht dann in \(v\)-Richtung und \(u\)-Richtung wieder zum Ausgangspunkt zurück. Das kann man sich als Motivation für die genaue Form von Krümmungstensor und Torsion merken.
Interessanterweise enthalten weder die Torsion noch die Krümmung Ableitungen der Tangentialvektoren, obwohl im Prinzip die kovarianten Ableitungen solche Terme erzeugen könnten. Grund: Durch die antisymmetrische Struktur fallen diese Terme jeweils weg. Als Folge davon hängt die Torsion nur von Christoffelsymbolen (genauer: von deren antisymmetrischen Anteil) ab \[ T^{ \rho}_{\nu\mu} := \Gamma^{ \rho}_{\nu\mu} - \Gamma^{ \rho}_{\mu\nu} \] während die Krümmung zusätzlich noch erste Ableitungen der Christoffelsymbole enthält: \[ R^{\mu}_{\,\nu\rho\sigma} = \frac{\partial \Gamma^{ \mu}_{\sigma\nu}}{\partial x^{\rho}} - \frac{\partial \Gamma^{ \mu}_{\rho\nu}}{\partial x^{\sigma}} + \] \[ + \sum_{\alpha} \, \left( \Gamma^{ \mu}_{\rho\alpha} \, \Gamma^{ \alpha}_{\sigma\nu} - \Gamma^{ \mu}_{\sigma\alpha} \, \Gamma^{ \alpha}_{\rho\nu} \right) \] Terme mit Ableitungen von \(u\), \(v\) oder \(w\) gibt es bei \(R(u, v) \, w\) oder \(T(u, v)\) nicht. Dadurch wird die Linearität in \(u\), \(v\) und \(w\) sichergestellt.
Man kann die koordinatenfreie Darstellung des Krümmungstensors etwas umstellen und dadurch den foldenden Ausdruck für das Vertauschen kovarianter Ableitungen gewinnen: \[ D_{u} D_{v} - D_{v} D_{u} = R(u,v) + D_{[u, v]} \] Den Term \( D_{[u, v]} \) kann man wiederum mit Hilfe der Torsion ausdrücken, was wir hier aber weglassen wollen. Man bezeichnet die entsprechende Gleichung auch als Ricci-Identität.
Der Krümmungstensor ist wie die Torsion antisymmetrisch in \(u\) und \(v\). Man kann sich weiter fragen, ob der Ausdruck \( R(u, v) \, w \) weitere Symmetrien bzgl. \(w\) aufweist. Eine solche wichtige Symmetrie ist im torsionsfreien Fall die Folgende:
Ist die Torsion gleich Null, so gilt \[ \; R(u, v) w + \] \[ + R(v, w) u + \] \[ \; + R(w, u) v = 0 \] Bei nichtverschwindender Torsion steht dagegen auf der rechten Seite ein Term, der Ableitungen der Torsion enthält. Insofern gibt es durchaus gewisse Zusammenhänge zwischen Torsion und Krümmungstensor.
Außerdem gilt:
Es gilt (unabhängig von der Torsion) \[ \; D_{u} R(v, w) + \] \[ + D_{v} R(w, u) + \] \[ \; + D_{w} R(u, v) = 0 \] oder in Cartans Schreibweise \[ dR = R \wedge \Theta - \Theta \wedge R \] wie man aus \( R = d\Theta + \Theta \wedge \Theta \) ableiten kann (überspringen wir hier).
Eine kleine Übung zum Abschluss:
Wir wollen uns einmal den Krümmungstensor zu
den total antisymmetrischen Christoffelsymbolen aus
Kapitel 7:
Torsion ansehen.
Zur Erinnerung: Wir betrachten
\[
\Gamma^{ \rho}_{\nu\mu}
= \epsilon^{\rho}_{\,\nu\mu}
\]
Dabei ist \( \epsilon^{ \rho}_{\,\nu\mu} \)
gleich Null für zwei gleiche Indizes, antisymmetrisch bei Vertauschung zweier Indices
und es ist \( \epsilon^{1}_{\,2 3} =
\epsilon^{2}_{\,3 1} = \)\(\epsilon^{3}_{\, 1 2} = 1 \).
Eine kurze Rechnung ergibt:
\[
R^{\mu}_{\,\nu\rho\sigma} =
\delta_{\mu\sigma} \, \delta_{\rho\nu} -
\delta_{\mu\rho} \, \delta_{\sigma\nu}
\]
Überaschenderweise ist die Krümmung also nicht Null, obwohl die
geodätischen Linien Geraden sind. Im nächsten Kapitel werden wir
den Zusammenhang zwischen Metrik und affinem Zusammenhang untersuchen.
Vielleicht verstehen wir dann diesen überaschenden Sachverhalt besser.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 22 September 2023