Vieles spricht dafür, dass die Stringtheorie zusammen mit der Supersymmetrie wesentliche Ideen für eine allumfassende physikalische Theorie enthält und vermutlich ein wichtiger Schritt dahin ist. So kommt in der Stringtheorie die Gravitation gleichsam nebenbei heraus, und zwar in einer quantisierbaren Form. Die Stringtheorie ist also eine funktionierende Basis für eine Quanten-Gravitationstheorie. Außerdem ist die Stringtheorie so reich an Strukturen, dass auch die anderen Naturkräfte in ihr im Prinzip beschrieben werden können.
Es lohnt sich also, wenn wir uns zumindest grob mit der Stringtheorie beschäftigen und zu versuchen, einige der wesentlichen Ideen zu verstehen. Mehr zu den Grundideen finden Sie beispielsweise auch in den beiden populärwissenschaftlichen Bücher von Brian Greene: Das elegante Universum, 2002, ISBN 3442760267 und Der Stoff, aus dem der Kosmos ist - Raum, Zeit und die Beschaffenheit der Wirklichkeit, 2004, ISBN 388680738 sowie in der dazugehörenden TV-Dokumentation von Brian Greene The Elegant Universe (Video auf der Webseite verfügbar).
Wie schon im vorherigen Kapitel über Supersymmetrie ist es auch bei der Stringtheorie unmöglich, sie in einem Kapitel im Detail zu verstehen. Schließlich gibt es ganze Bücher zu dem Thema. Dennoch sollte es möglich sein, wenigstens die Grundideen grob zu erfassen. Das wollen wir hier versuchen. Mühsame Rechnungen oder überlange Formeln werde ich dabei weglassen oder sie nur grob schematisch darstellen, um ihre Struktur sichtbar zu machen. Fangen wir also an!
Im ersten Schritt wollen wir uns klassische relativistische Strings ansehen. Eine gute Darstellung dazu können Sie beispielsweise in Gerard 't Hooft: Introduction to String Theory, Kapitel 2 finden. An dieser Darstellung werde ich mich hier teilweise orientieren.
Klassische relativistische Strings sind unendlich dünne Fäden aus reiner Energie (bzw. Masse), die sich durch den Raum bewegen. Quanteneffekte spielen dabei noch keine Rolle – sie kommen später. Solche klassischen Strings gibt es in der Natur so zunächst nicht. Wenn wir aber später Quanteneffekte berücksichtigen, so können wir extrem winzige quantisiserte Strings als Elementarteilchen auffassen und so theoretisch eine Quantentheorie aller Natürkräfte aufbauen.
Zurück zu den klassischen Strings. Wir stellen uns vor, dass ein String nichts anderes ist als ein winziger Faden aus reiner Energie (bzw. Masse), die sich gleichmäßig entlang einer eindimensionalen Linie oder Kurve (dem Faden) im Raum verteilt. Die Frage "Woraus besteht ein String" ist damit so beantwortet: "Aus reiner Energie".
Die Energiedichte bzw. Massendichte entlang eines ruhenden String-Teilstücks soll überall am String gleich groß sein. Anders ausgedrückt: der String besitzt eine konstante Massendichte pro Länge. Dabei ist mit dieser Massendichte bzw. Energiedichte immer die Ruhemasse bzw. Ruheenergie pro Stringlänge im Ruhesystem des jeweiligen Stringstücks gemeint.
Wenn wir einen String verlängern, so müssen wir ihm dazu Energie zuführen, um das neue Stringstück mit derselben Massendichte zu versehen wie die alten Stringstücke. Der String verhält sich also nicht wie ein Gummi, sondern eher wie eine Flussröhre eines Magnetfeldes mit konstanter Feldstärke.
Klassisch kann man sich vorstellen, dass man zur Verlängerung eines Strings an einem seiner Enden ziehen muss. Wenn man dabei gegen eine konstante Zugkraft \(F\) des Strings ankämpfen muss, so braucht man zur Stringverlängerung um die Länge \(ds\) eine Energiemenge \[ dE = F \, ds \] (\(ds\) ist dabei die räumliche Bogenlänge des Stringstücks, alles im Ruhesystem angegeben).
Diese Energiemenge \(dE\) benötigen wir in unserem Bild, um die Masse des neuen Stringstücks der Länge \(ds\) aufzubauen. Die Massen- bzw. Energiedichte \[ \frac{dE}{ds} = F \] kann man also als Zugkraft oder Zugspannung (engl. string tension) des Strings auffassen. Sie wird meist mit \(T\) (statt \(F\)) bezeichnet: \[ \frac{dE}{ds} = F =: T \] Da unser String eine konstante Massendichte haben soll (egal wie lang er ist), hat er auch eine konstante Zugspannung, egal wie lang er ist – anders als ein Gummi, bei dem normalerweise die Zugkraft linear mit der Abweichung von einer Grundlänge anwächst.
Im Folgenden wollen wir wie üblich die Einheiten so wählen, dass die Lichtgeschwindigkeit aus den Formeln herausfällt. Massen werden also in Energieeinheiten gemessen, Längen in Lichtsekunden und Geschwindigkeiten in Bruchteilen der Lichtgeschwindigkeit.
Wir wollen uns den String vollkommen strukturlos vorstellen. Das bedeutet: Die einzige Möglichkeit, einem ruhenden String Energie zuzuführen, besteht darin, ihn zu verlängern oder aber ihn in Bewegung (z.B in räumliche Schwingungen) zu versetzen.
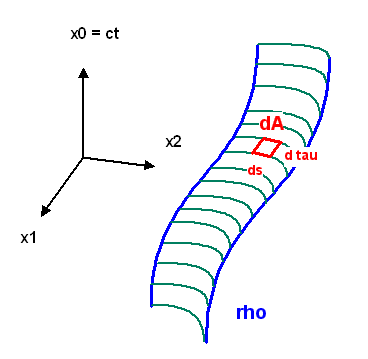
Versuchen wir, mit diesem Bild im Hintergrund ein einfaches relativistische Wirkungsfunktional aufzustellen, aus dem man die Bewegungsgleichungen als Euler-Lagrange-Gleichungen ermitteln kann (siehe Quantenfeldtheorie und Eichfelder, Kapitel 3 und folgende). Den String wollen wir durch die räumliche Bogenlänge \(s\) parametrisieren, d.h. der dreidimensionale Ortsvektor \( \boldsymbol{x}(s) \) ist ein Raumpunkt auf dem String und \(ds\) ist die räumliche Länge eines dort liegenden infinitesimalen Stringstücks in seinem Ruhesystem.
Die Freiheitsgrade des Strings sind nun an jeder Stelle \( \boldsymbol{x}(s) \) des Strings durch die beiden Raumrichtungen senkrecht zur Stringrichtung gegeben – Bewegungen in Stringrichtungen sind bedeutungslos, da der String strukturlos ist.
Um die Lagrangefunktion für die Wirkung aufzustellen, lassen wir uns von der relativistischen Lagrangefunktion eines freien Teilchens leiten. Aus Kapitel 5.2 wissen wir:
Ein kräftefreier Körper bewegt sich zwischen zwei vorgegebenen Raum-Zeit-Punkten auf derjenigen Kurve mit extremaler (genauer: maximaler) Eigenzeit (Trödelprinzip).
Das gilt sogar in Anwesenheit von Gravitation. Gleichbedeutend damit ist, dass die Raum-Zeit-Bahnkurve (Weltlinie) des Körpers eine Geodäte in der Raumzeit ist.
Als Wirkungsfunktional \(S\) für eine Raum-Zeit-Kurve \( \rho \) eines freien Teilchens können wir also die Eigenzeit \( \tau \) entlang der Kurve nehmen, also die Zeit, die auf einer Uhr verstreicht, die sich mit dem Teilchen entlang der Kurve durch Raum und Zeit bewegt.
Ein sich frei bewegendes Teilchen wird sich dann zwischen zwei vorgegebenen Raum-Zeit-Punkten auf derjenigen Kurve (Weltlinie) bewegen, bei der auf der mitgeführten Uhr die maximale Zeit verstreicht. Das Prinzip der extremalen Wirkung (hier der maximalen Eigenzeit) sorgt dann dafür, dass die Euler-Lagrange-Gleichungen genau die richtigen Bewegungsgleichungen ergeben.
Meist multipliziert man die Eigenzeit noch mit der Ruhemasse \(m\) des Objektes, um die physikalische Dimension einer Wirkung (Energie mal Zeit) zu erhalten, und mit einem Vorzeichen, so dass eine maximale Eigenzeit einer minimalen Wirkung entspricht. \[ S[\rho] := - m \int_{\rho} d\tau \] Nun ersetzen wir das Teilchen durch ein infinitesimales Stringstück der Länge \(ds\). Die Ruhemasse \(m\) dieses kleinen Stringstücks ist gegeben durch \( T \, ds \), wir wir von oben bereits wissen. Setzen wir dies für \(m\) ein und summieren (integrieren) alle Wirkungsbeiträge für die einzelnen Stringstücke zu einer Gesamtwirkung für den String auf, so erhalten wir: \[ S[\rho] := - \int_{\rho} T \, ds \, d\tau \] Dabei ist \(\rho\) hier die zweidimensionale Fläche in der Raumzeit, die der eindimensionale String im Lauf der Zeit durchläuft, und \(ds\) ist die Bogenlänge des kleinen Stringstücks im lokalen Ruhesystem. Die String Tension (Massendichte) \(T\) soll konstant sein, d.h. wir können sie aus dem Integral herausziehen.
Der Ausdruck \[ ds \, d\tau \] ist ein invariantes Flächenelement \(dA\) in der Raumzeit (\(T\) ist sowieso konstant). Sowohl die Eigenzeit \(d\tau\) als auch die Bogenlänge \(ds\) sind dabei Poincaré-invariante Größen – wir werden es gleich noch explizit sehen, wobei \(ds\) nur im Ruhesystem des Stringstücks die Bedeutung der Bogenlänge hat (so wie \(d\tau\) nur im Ruhesystem des Stringstücks die Bedeutung der verstreichenden Zeit hat).
Man könnte auch sagen: \(d\tau\) ist die auf einer mitbewegten Uhr angezeigte Zeit, und \(ds\) ist die auf einem mitbewegten Längenmaßstab angezeigte Bogenlänge.
Da nun \(ds\) und \(d\tau\) Poincaré-invariante Größen sind, so ist auch das Flächenelement \[ dA = ds \, d\tau \] Poincaré-invariant. Es ist hier nur in einer bestimmten Parametrisierung dargestellt, die durch die lokale Eigenzeit und die lokale Ruhe-Bogenlänge gegeben ist.

In Gekrümmte Räume, Kapitel 11
können Sie nachlesen, wie ein invariantes Flächenelement \(dA\) in einem (sogar ggf. gekrümmten)
Raum mit einer Metrik in einer beliebigen Parametrisierung aussieht:
\[
dA = \sqrt{ |\det{G}| } \, d\sigma_{1} \, d\sigma_{2}
\]
mit der Gramschen Matrix
\[
G_{ij} = g(u_{i}, u_{j} )
\]
Dabei bilden die beiden reellen Parameter \(\sigma_{1}\) und \(\sigma_{2}\) eine beliebige Parametrisierung
der Fläche, \(u_{1}\) und \(u_{2}\) sind die zugehörigen Tangentialvektoren und \(g\) ist die
Metrik dieser Tangentialvektoren, hier also die Minkowski-Metrik.
Die Gramsche Matrix \(G_{ij}\) liefert die auf der String-Weltfläche induzierte Metrik, und zwar in der Matrixdarstellung bezüglich der gewählten Flächenparametrisierung.
Anmerkung:
In Gekrümmte Räume, Kapitel 11
haben wir die Bezeichnung \(t_{i}\)
statt \(\sigma_{i}\) verwendet, aber das verwechselt man hier zu schnell mit Zeitkoordinaten.
Oft nennt man einen der beiden Parameter \(\tau\) und den anderen Parameter \(\sigma\), wobei die entsprechenden
Tangentialvektoren zeitartig bzw. raumartig gewählt werden, so dass man \(\tau\) als zeitlichen
und \(\sigma\) als räumlichen Parameter interpretieren kann. Dabei muss \(\tau\) nicht unbedingt die
lokale Eigenzeit sein.
Die Wirkung des klassischen relativistischen Strings lautet also:
| \[ S[\rho] := - T \, \int_{\rho} dA = \] \[ = - T \, \int_{\rho} \sqrt{ |\det{G}| } \, d\sigma_{1} \, d\sigma_{2} = \] \[ = - T \, \int_{\rho} \sqrt{ | G_{11} G_{22} - G_{12}^{2} | } \, d\sigma_{1} \, d\sigma_{2} = \] \[ =: \int_{\rho} \, \mathcal{L} \, d\sigma_{1} \, d\sigma_{2} \] |
mit der Langrangedichte \(\mathcal{L}\).
Man nennt diesen Ausdruck die Nambu-Goto-Wirkung. Sie ist unabhängig von der Parametrisierung der Fläche, die der String bei seiner Wanderung in der Raumzeit durchläuft. Er ist offensichtlich auch invariant bei Poincarétransformationen, denn diese ändern die Matrixelemente \( G_{ij} = g(u_{i}, u_{j}) \) nicht (wir haben hier sogar eine koordinatenunabhängige Schreibweise gewählt, in der diese Invarianz unmittelbar sichtbar ist).
Während bei einem Punktteilchen die Wirkung durch die Vierer-Länge (Eigenzeit) der Bahnkurve (Weltlinie) in der Raumzeit gegeben ist, ist sie für einen String durch die Fläche in der Raumzeit gegeben, die der String durchläuft. Gemeint ist natürlich nicht eine wirkliche Fläche, sondern eine Verallgemeinerung des Flächenbegriffs, bezogen auf die Minkowski-Metrik.
Können wir aus der obigen Formel unseren Start-Ausdruck \[ S[\rho] := - \int_{\rho} T \, ds \, d\tau \] zurückerhalten, bei dem \(\tau\) die Eigenzeit für ein Stringstück der Ruhe-Bogenlänge \(ds\) ist? Das geht, und zwar so:
Wenn \[ \sigma_{1} = \tau \] die Eigenzeit sein soll, so muss der entsprechende Tangentialvektor (also die Vierergeschwindigkeit) \(u_{1}\) auf Eins normiert sein (wir setzen ja die Lichtgeschwindigkeit auf Eins) – siehe Kapitel 3,7: \[ G_{11} = g(u_{1}, u_{1} ) = 1 \] Damit hätten wir das erste der vier Matrixelemente der Gramschen Matrix. Zur Erinnerung: die Minkowski-Metrik hatten wir so definiert, dass \[ g(x,x) = (x^{0})^{2} - \boldsymbol{x}^{2} \] ist.
Den zweiten Parameter \[ \sigma_{2} = s \] wollen wir so wählen, dass \[ G_{12} = g(u_{1}, u_{2} ) = 0 \] ist (natürlich ist wegen der Symmetrie der Metrik sowieso \( G_{12} = G_{21} \)). Im lokalen Ruhesystem des kleinen Stringstücks bedeutet das: Weil \(u_{1}\) dort nur eine zeitliche und keine räumliche Komponente hat (die räumliche Geschwindigkeit des Stringstücks ist im lokalen Ruhesystem ja Null), kann \(u_{2}\) dort nur eine räumliche Komponente haben, d.h. \(u_{2}\) ist ein räumlicher Tangentialvektor in Stringrichtung an dieser Stringstelle und \(u_{2}^0 = 0\).
Wir können nun die Parametrisierung wieder so wählen, dass \[ G_{22} = g(u_{2}, u_{2} ) = - 1 \] ist. Im lokalen Ruhesystem des Stringstücks bedeutet das, dass \[ (\boldsymbol{u}_{2})^{2} = 1 \] ist. Aus Kapitel 5.1.11 wissen wir, dass dieses \(s\) dann die räumliche Bogenlänge des Strings ist.
Mit der Eigenzeit \(\tau\) und der Bogenlänge \(s\) als Parameter ist die Determinante des Betrags der Gramschen Matrix gleich Eins (die vier Matrixelemente hatten wir ja gerade angegeben), und die Wirkung ist \( S[\rho] = - \int_{\rho} T \, ds \, d\tau \) wie oben angegeben.
Damit haben wir unser erstes Ziel schon erreicht:
Wir kennen das Wirkungsfunktional eines
klassischen relativistischen Strings – es war gar nicht so schwer.
Damit können wir nun loslegen und klassische Bewegungsgleichungen (Euler-Lagrange-Gleichungen) aufstellen. Das können wir analog zu Quantenfeldtheorie und Eichfelder, Kapitel 4 machen:
Die beiden Flächenparameter \( \sigma_{i} \) des Strings entsprechen dabei den 4 Raumzeitkoordinaten \( x = (x^{\mu}) \), die String-Weltfläche \( \rho(\sigma_{1}, \sigma_{2}) \) entspricht den Feldern \(\Phi_{k}(x)\) und die beiden Tangentialvektoren \( u_{i} = \frac{\partial \rho}{\partial \sigma_{i}} \) entsprechen den Feldableitungen \( \delta_{\mu} \Phi_{k} = \frac{\partial \Phi_{k}}{\partial x^{\mu}} \) (da wir eine Einbettung des Strings in der vierdimensionalen Raumzeit haben, können wir das problemlos so schreiben).
Damit können wir die Euler-Lagrange-Gleichungen durch Vergleich mit der entsprechenden Formel \[ \frac{d\mathcal{L}}{d\Phi_k} - \partial_\mu \frac{d\mathcal{L}}{d \, (\partial_\mu \Phi_k)} = 0 \] aus Quantenfeldtheorie und Eichfelder, Kapitel 4 direkt hinschreiben, wobei wir die Schreibweise \(\rho^{\mu}\) und \(u_{i}^{\mu}\) für die 4 Raumzeit-Koordinaten eines Punktes auf der String-Weltfläche bzw. die Raumzeit-Komponenten der Tangentialvektoren verwenden (dieser Index \(\mu\) entspricht dabei dem Feldindex \(k\) in \(\Phi_{k}\)). An dieser Stelle kommen also die Koordinaten der Raumzeit zum ersten Mal konkret ins Spiel! Bisher hatten wir alle Gleichungen koordinatenfrei formuliert.
| \[ \frac{d \mathcal{L}}{d \rho^{\mu}} - \frac{\partial}{\partial \sigma_{1}} \frac{d\mathcal{L}}{d u_{1}^{\mu}} - \frac{\partial}{\partial \sigma_{2}} \frac{d\mathcal{L}}{d u_{2}^{\mu}} = 0 \] |
Die Lagrangedichte \[ \mathcal{L}(\rho, u_{1}, u_{2}) = - T \, \sqrt{ |\det{G}| } = \] \[ = - T \, \sqrt{ | G_{11} \, G_{22} - G_{12}^{2} | } = \] \[ = - T \, \sqrt{ | ( u_{1}^{\mu} \, u_{1 \mu} ) \, (u_{2}^{\nu} \, u_{2 \nu} ) - ( u_{1}^{\mu} \, u_{2 \mu} )^{2} | } \] (mit Summation über \(\mu\) und \(\nu\)) ist dabei eine Funktion reeller Zahlen in die reellen Zahlen, d.h. man muss alle Ausdrücke für bestimmte Parameterwerte \(\sigma_{i}\) auswerten.
Anders die Wirkung: Sie ist ein Funktional von einem Funktionenraum in die reellen Zahlen.
Bei Strings entfällt sogar die Abhängigkeit von \(\rho\), so dass der erste Term in der Lagrangegleichung wegfällt. Ganz analog ist es in der klassischen Mechanik für ein freies Teilchen, das sich auf einer ggf. gekrümmten Fläche bewegt (Stichwort Zwangsbedingung).
Bei der Ableitung der Euler-Lagrange-Gleichungen muss man Randbedingungen für die Fläche vorgeben, so dass beim partiellen Integrieren (Integralsatz von Stokes, siehe Gekrümmte Räume, Kapitel 11) die Randterme für den Rand \(\delta\rho\) der String-Weltfläche wegfallen. Diese Bedingung können wir in Quantenfeldtheorie und Eichfelder, Kapitel 4 ablesen (siehe die dortige Herleitung der Euler-Lagrange-Gleichungen) und wieder auf den String übersetzen. Man muss diese Randbedingungen dann genauer analysieren und betrachtet dabei offene und geschlossene Strings. Wir wollen uns das hier nicht genauer ansehen.
Die Wurzel in der Lagrangedichte verkompliziert die Euler-Lagrange-Gleichungen erheblich. Es wäre daher schön, die Wurzel \[ \sqrt{ | G_{11} \, G_{22} - G_{12}^{2} | } \] loszuwerden.
Eine Möglichkeit dazu hatten wir oben schon genutzt, indem wir als Parameter die Eigenzeit und die Bogenlänge gewählt haben, sodass der zweite Term unter der Wurzel wegfällt und der erste Term 1 wird.
Eine andere Möglichkeit besteht darin, dafür zu sorgen, dass der erste Term gleich Null und der zweite Term gleich Eins wird. Um Verwirrung zu vermeiden, wollen wir die entsprechenden Parameter mit \[ \sigma_{+} , \, \sigma_{-} \] bezeichnen. Analog schreiben wir kurz beispielsweise \( G_{++} \) für \( g(u_{+} , u_{+} ) \). In dieser Parametrisierung soll also \[ G_{++} = G_{--} = 0 \] sein. Das bedeutet, dass die Tangentialvektoren (Vierervektoren) \(u_{+}\) und \(u_{-}\) lichtartig sind, so wie die Vierergeschwindigkeit masseloser Teilchen. Daher der Begriff Lichtkegelkoordinaten.
An \( G_{+ -} \) stellen wir keine Forderung.
Damit fällt die Wurzel in Lichtkegelkoordinaten weg und wir haben \[ S[\rho] = - T \, \int_{\rho} |G_{+ -}| \, d\sigma_{+} \, d\sigma_{-} \] Wenn man von zwei Parametern \( \sigma_{1} = \tau \) und \( \sigma_{2} = \sigma \) ausgeht, die \( G_{12} = G_{21} = 0 \) sowie \( G_{11} = - G_{22} \) erfüllen (beispielsweise Eigenzeit und Bogenlänge), dann kann man Lichtkegelkoordinaten auf die folgende Weise definieren: \[ \sigma_{+} := a \cdot (\sigma + \tau) \] \[ \sigma_{-} := a \cdot (\sigma - \tau) \] mit einer beliebigen reellen Zahl \(a\). Bei Eigenzeit und Bogenlänge wählt man oft \( a = 1/\sqrt{2} \).
In Lichtkegelkoordinaten kann man die Euler-Lagrange-Gleichungen (Bewegungsgleichungen) nun leicht aufstellen und lösen. Aus der Lagrangefunktion \[ \mathcal{L}(\rho, u_{+}, u_{-} ) = \] \[ = - T \, g(u_{+} , u_{-} ) = \] \[ - T \, g_{\mu\nu} \, u_{+}^{\mu} \, u_{-}^{\nu} \] (mit Summation über doppelte Indizes) ergibt sich bei konstanten Metrik \[ \frac{\partial}{\partial \sigma_{+}} \frac{d\mathcal{L}}{du_{+}^{\mu}} + \frac{\partial}{\partial \sigma_{-}} \frac{d\mathcal{L}}{du_{-}^{\mu}} = \] \[ = - T \, g_{\mu\nu} \left( \frac{\partial u_{-}^{\nu}}{\partial \sigma_{+}} + \frac{\partial u_{+}^{\nu}}{\partial \sigma_{-}} \right) = 0 \] Das können wir mit Hilfe der inversen metrischen Matrix vereinfachen zu \[ \frac{\partial u_{-}^{\mu}}{\partial \sigma_{+}} + \frac{\partial u_{+}^{\mu}}{\partial \sigma_{-}} = 0 \] Mit \( u_{+}^{\mu} = \frac{\partial \rho^{\mu}}{\partial \sigma_{+}} \) usw. folgt \[ \frac{\partial}{\partial \sigma_{+}} \frac{\partial}{\partial \sigma_{-}} \rho^{\mu} + \frac{\partial}{\partial \sigma_{-}} \frac{\partial}{\partial \sigma_{+}} \rho^{\mu} = 0 \] Wir gehen davon aus, dass die Ableitungen vertauschbar sind, so dass wir schließlich die einfache Bewegungsgleichung \[ \frac{\partial}{\partial \sigma_{+}} \frac{\partial}{\partial \sigma_{-}} \rho^{\mu} = 0 \] erhalten. Diese Gleichung ist durch den Ansatz \[ \rho(\sigma_{+},\sigma_{-}) = a \, (\sigma_{+}) + b \, (\sigma_{-}) \] mit zwei Funktionen \(a\) und \(b\) einfach lösbar. Ich überspringe das hier – man kann es z.B. in Gerard 't Hooft: Introduction to String Theory auf Seite 9 nachlesen.
Eine weitere Möglichkeit, die Wurzel in der Lagrangefunktion bzw. Wirkung teilweise loszuwerden, ist der Folgende:
In der Wirkung fügen wir die Identität \[ 1 = \frac{1}{2} \, \mathrm{Spur} (G^{- 1} \, G) \] im Integranden hinzu: \[ S[\rho] = - T \, \int_{\rho} \sqrt{ |\det{G}| } \, \frac{1}{2} \, \mathrm{Spur} (G^{- 1} \, G) \, d\sigma_{2} \, d\sigma_{1} \] Nun vergessen wir vorübergehend für die Terme \(\det{G}\) und \(G^{- 1}\), dass die Matrix \(G\) darin von den Tangentialvektoren abhängt, und behandeln sie als unabhängige dynamische Freiheitsgrade. Nur die ganz rechts stehende Matrix \(G\) ersetzen wir durch die entsprechenden Ausdrücke in den Tangentialvektoren. \[ S[\rho] = \] \[ = - T \, \int_{\rho} \sqrt{ |\det{G}| } \, \frac{1}{2} \, \sum_{ij} \, (G^{- 1})_{ij} \, g(u_{i},u_{j}) \, d\sigma_{2} \, d\sigma_{1} \] Man nennt diesen Ausdruck die Polyakov-Wirkung. Damit haben wir die Anzahl der Freiheitsgrade allerdings erhöht. Die Variation der Wirkung ergibt nun neue Euler-Lagrange-Gleichungen für die Freiheitsgrade, also auch für die Matrixelemente von \(G\). Dabei ergibt sich u.a. die Bewegungsgleichung \[ G_{ij} = C(\sigma_{1},\sigma_{2}) \, g(u_{i},u_{j}) \] Die reelle Funktion \( C(\sigma_{1},\sigma_{2}) \) wird konformer Faktor genannt. Setzen wir diese Gleichung in die Polyakov-Wirkung ein, so fällt \( C(\sigma_{1},\sigma_{2}) \) heraus, so dass wir die alte Nambu-Goto-Wirkung sowie die korrekten Euler-Lagrange-Gleichungen zurückerhalten.
Man kann nun die Parametrisierung der String-Weltfläche geschickt wählen, so dass die Matrix \(G\) sehr einfach wird. Eine gute Darstellung dazu findet man z.B. in Richard J. Szabo: BUSSTEPP Lectures on String Theory, hep-th/0207142, Seite 15.
Damit wollen wir es mit mathematischen Details genug sein lassen. Immerhin ist es beruhigend, dass wir in der Lage sind, das Wirkungsfunktional zu verstehen und die Euler-Lagrange-Gleichungen aufzuschreiben, zusammen mit den Randbedingungen. Nun beginnt die eigentliche Arbeit: die Analyse der Gleichungen und Randbedingungen sowie die Lösung der Bewegungsgleichungen. Dabei spielen auch Begriffe wie Energie-Impuls-Tensor, Schwerpunktsbewegung, Drehimpuls und Schwingungsmoden eine Rolle. Wir wollen uns die mühsamen Details hier ersparen. Immerhin können wir uns vorstellen, dass der String sich als Ganzes bewegen kann, dass er rotieren und schwingen kann und dass man all diese Aspekte in den Lösungen der Bewegungsgleichungen wiederfindet.
Wenn man die klassische Stringtheorie gut genug verstanden hat, kann man versuchen, sie zu quantisieren. Wie so etwas im Prinzip geht, kann man in Quantenfeldtheorie und Eichfelder, Kapitel 2, Kapitel 3, Kapitel 4 und Kapitel 5 nachlesen. Hier sind noch einmal die wesentlichen Ideen:
Im üblichen Ansatz sucht man einen passenden Hilbertraum, dessen Vektoren die möglichen Quantenzustände darstellen. Meist kann ein solcher Vektor als geeigntete Funktion auf der Raumzeit dargestellt werden. Die Wahrscheinlichkeitsamplituden sind dann durch ein passendes Skalarprodukt gegeben. Freie Teilchen entsprechen ebenen Wellen, wobei der Viererimpuls \(p\) des Teilchens über \[ p = \hbar k \] durch den Wellenvektor \(k\) gegeben ist.
Die dynamischen Variablen (Observablen) der klassischen Theorie werden nun durch hermitesche Operatoren auf dem Hilbertraum dargestellt. Die Werte, die diese Variablen annehmen können, entsprechen den Eigenwerten der Operatoren. Die Zeitentwicklung der Quantenzustände muss so gewählt werden, dass sich die quantenmechanischen Mittelwerte der Observablen wie wie die zugehörigen klassischen Größen verhalten (bis auf Terme proportional zu Potenzen des Planckschen Wirkungsquantums).
Eine etablierte Vorgehensweise besteht darin, die klassische Theorie in eine Hamiltonsche Formulierung mit antisymmetrischen Poissonklammern zu bringen. Die algebraische Struktur dieser Poissonklammern kann man dann in eine analoge algebraische Struktur von Kommutatoren der Operatoren in der Quantentheorie übersetzen. Das nennt man auch kanonische Quantisierung.
Eine Alternative ist die Pfadintegralquantisierung nach Feynman und Dirac. Sie basiert auf der Lagrange-Formulierung der klassischen Theorie. Dabei wird eine Wahrscheinlichkeitsamplitude zwischen einem Anfangs- und einem Endzustand über die Interferenzregel berechnet, d.h. es werden alle denkbaren Möglichkeiten aufintegriert, die von dem Anfangszustand zum Endzustand führen können. Jede Möglichkeit trägt dabei mit einer Amplitude bei, die proportional zu \[ e^{i S[\rho] / \hbar} \] ist. Dabei ist \(S\) die Wirkung der Funktion \(\rho\), die zu dieser Möglichkeit gehört. In unserem Fall ist \(\rho\) eine String-Weltfläche, die die Entwicklung eines Strings durch die Zeit darstellt. Diese String-Weltfläche muss keine Lösung der Bewegungsgleichung sein (diese Lösungen entsprechen ja dem Minimum von \(S\)). Auf diese Weise werden alle Quantenfluktuationen erfasst, die von der Lösung der Bewegungsgleichungen abweichen.
Die Quantisierung bei Strings hat viele Ähnlichkeiten mit der Quantisierung von Eichtheorien. Der Umeichung der Eichpotentiale entspricht hier die Umparametrisierung der String-Weltfläche. Daher wundert es nicht, dass man sich bei der Quantisierung der Stringtheorie mit denselben Problemen herumschlagen muss wie in der Eichtheorie (siehe Quantenfeldtheorie und Eichfelder, Kapitel 5).
Man kann z.B. die Parametrisierung vor oder nach der Quantisierung fixieren und muss dann ggf. die Unabhängigkeit der Quantentheorie von der gewählten Parametrisierung nachweisen. Berücksichtigt man Randbedingungen erst nach der Quantisierung, so ist der entstandene Hilbertraum zunächst zu groß und muss geeignet reduziert werden (d.h. die Randbedingungen werden dann dadurch berücksichtigt).
Analog muss man bei den Pfadintegralen aufpassen, dass man jede Stringweltfläche nur einmal im Pfadintegral berücksichtigt und nicht verschiedene Umparametrisierungen mit berücksichtigt. Die Methode dazu ist bekannt, siehe Quantenfeldtheorie und Eichfelder, Kapitel 5, Stichwort: Faddeev-Popov-Determinante. Dabei treten sogenannte Geistfelder auf, die die entsprechende Buchhaltung sicherstellen.
Wie sieht nun die Quantentheorie von Strings aus? Nun, Stringzustände haben zunächst einmal eine Schwerpunktsbewegung analog zu einem Atom in der üblichen Quantentheorie. Dies entspricht einer ebenen Welle. Hinzu kommen innere Schwingungen und Rotationen, die u.a. durch unendlich viele harmonische Oszillatoren dargestellt werden können (ähnlich wie bei einem Feld).
Insgesamt ist die Konstruktion des Hilbertraums nicht ohne Probleme. So treten bei der Quantisierung unphysikalische Zustände auf, z.B. Zustände mit negativer Norm. Eine genaue Analyse (No-Ghost-Theorem) zeigt, dass der Hilbertraum nur dann alle Anforderungen erfüllt, wenn die Raumzeit 26-dimensional ist (eine Zeitdimension, 25 Raumdimensionen).
Die unphysikalischen Zustände kann man vermeiden, wenn man die klassische Theorie in Lichtkegelkoordinaten formuliert und quantisiert. Allerdings muss man später überprüfen, ob die Quantentheorie noch Poincaré-kovariant ist, also verträglich ist mit der speziellen Relativitätstheorie. Auch hier zeigt sich: das ist wieder nur der Fall, wenn die Raumzeit 26-dimensional ist.
Sogar die Pfadintegralquantisierung erfüllt nur dann alle Anforderungen, wenn die Raumzeit 26-dimensional ist. Die Details lasse ich hier weg.
Es tritt noch ein ungewöhnliches Phänomen bei der Quantisierung auf: Es zeigt sich, dass der Hilbertraum einen Zustand mit negativem Massenquadrat enthält. Man kann sich überlegen, dass dies einem sogenannten Tachyon entspricht, also einem Teilchen, das sich mit Überlichtgeschwindigleit bewegt (Star Treck Fans atmen auf). So ein Teilchen ist aus verschiedenen Gründen physikalisch nicht akzeptabel. Normalerweise signalisiert es, dass das Vakuum der Quantentheorie instabil ist, also nicht der Zustand niedrigster Energie ist. Erst die Supersymmetrie ist in der Lage, dieses Tachyon aus der Theorie zu entfernen.
Um von den 26 Dimensionen auf die üblichen 4 Raumzeit-Dimensionen zu kommen, muss man 22 dieser Dimensionen eng aufwickeln, also kompaktifizieren, so dass sie in den heute experimentell zugänglichen Energiebereichen keine Rolle spielen. Dies kann man auf verschiedene Arten tun. Die einfachste Möglichkeit besteht darin, einen mehrdimensionalen Torus zu bilden (so wie man bei einer Dimension einen Kreis bildet). Den Radius des Torus in einer Dimension bezeichnet man oft als \(R\), d.h. nach einer Wanderung um \(2 \pi R\) entlang einer aufgewickelten Dimension landet man wieder am Ausgangspunkt.
Ein Beispiel: Kompaktifiziert man bei einer zweidimensionalen Fläche eine der beiden Dimensionen, so erhält man eine Zylinder-Oberfläche mit Radius \(R\):
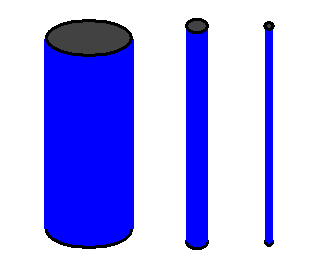
Das Aufrollen von Dimensionen hat zwei Folgen:
Man macht nun eine interessante Beobachtung: Wenn wir in der Stringtheorie geschlossener Strings (also Schlaufen) den Zylinderradius \(R\) durch den Zylinderradius \(1/R\) ersetzen (gemessen in Planck-Längen) sowie die Impulsquantenzahl durch die Windungszahl ersetzen und umgekehrt, so bleiben alle Eigenschaften des Spektrums der Quantenzustände unverändert. Das nennt man T-Dualität.
Es macht demnach keinen Sinn, den Zylinderradius kleiner als 1 (der Planck-Länge) zu wählen, weil man doch nur wieder eine Quantentheorie erhält, wie man sie zuvor schon bei größerem \(R\) hatte. In diesem Sinn machen Abstände unterhalb der Planck-Länge in der Stringtheorie keinen Sinn mehr.
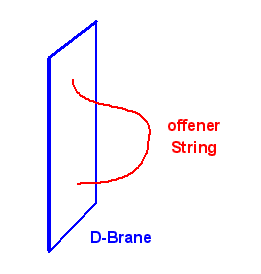
Bei offenen Strings wird man über die Randbedingungen dazu geführt, dass man neben den offenen Strings mit einer Raumdimension auch sogenannte D-Branes mit 24 Raumdimensionen braucht, die sich beide in 25 Raumdimensionen (plus eine Zeitdimension) bewegen. Der String endet gleichsam auf der D-Brane, so wie man im dreidimensionalen Raum die Enden eines Fadens an einer Fläche befestigen kann. Man hat herausgefunden, dass die Existenz eines Tachyons (siehe oben) etwas mit der Instabilität von D-Branes zu tun hat (siehe Washington Taylor, Barton Zwiebach: D-Branes, Tachyons, and String Field Theory, hep-th/0311017 ).
Man kann noch andere Dualitäten finden, und über ein Wechselspiel mit den Randbedingungen werden noch Branes mit anderen Dimensionen interessant. Es sieht so aus, als ob neben den Strings auch D-Branes zwangsläufig als Objekte in einer Stringtheorie auftreten (so kann man D-Branes als solitonartige – d.h. nicht auseinanderlaufende – Lösungen in der Stringtheorie ansehen). Die Details überspringen wir hier.
Die Supersymmetrie hatten wir uns bereits in Kapitel 6.1 angesehen. Sie tritt auf, wenn man in einer Theorie Bosonfelder und Fermionfelder geeignet miteinander mischen kann, so dass die Wirkung dabei unverändert bleibt. Dabei spielen auch Raumzeit-Ableitungen der Felder bei der Mischung eine Rolle – daher ist die Supersymmetrie mit den Raumzeitsymmetrien der Relativitätstheorie eng verwoben. Die Poincarégruppe wird zu einer Super-Poincarégruppe erweitert. Man kann eine Formulierung wählen, bei der die Raumzeitkoordinaten \(x^{\mu}\) um sogenannte Grassmann-Weyl-Spinoren erweitert werden, also um antikommutierende zweikomponentige Weyl-Spinoren. Auf dieser Super-Raumzeit ist nun die Super-Poincarégruppe definiert.
Warum Supersymmetrie? Nun, bereits in der normalen Quantenfeldtheorie hat die Supersymmetrie viele Aspekte, die sie zu einer attraktiven Symmetrie machen (siehe vorhergehendes Kapitel). Außerdem braucht man sie, um neben Bosonen auch Fermionen in der Stringtheorie beschreiben zu können. Zudem zeigt sich, dass sich viele Probleme der Stringtheorie mithilfe der Supersymmetrie lösen lassen – beispielsweise verschwindet das Tachyon.
Wie baut man nun Fermionen auf supersymmetrische Weise in die Stringtheorie ein, die bisher nur bosonische Strings enthält? In Gerard 't Hooft: Introduction to String Theory (S. 47) macht man das so:
Zu den bosonischen Raumzeitkoordinaten \[ \rho^{\mu}(\sigma_{1},\sigma_{2}) \] der String-Weltfläche kommen reelle fermionische Grassmann-Weyl-Spinoren \[ \psi^{\mu}(\sigma_{1},\sigma_{2}) \] hinzu, so wie man analog oben die Raumzeit um zusätzliche Grassmann-Dimensionen erweitert. Man hat jetzt so etwas wie eine String-Weltfläche in der supersymmetrisch erweiterten Raumzeit, die neben den Raumzeitkoordinaten noch Grassmannvariablen umfasst. Nicht über physikalische Interpretationen dieser Super-Raumzeit nachdenken – es handelt sich um einen formalen Trick, um alle bisherigen Formulierungen durch formale Analogien bequem auf antikommutierende (fermionische) Objekte übertragen zu können.
Wenn man will, kann man sich auch vorstellen, dass die \[ \psi^{\mu}(\sigma_{1},\sigma_{2}) \] gleichsam auf der zweidimensionalen String-Weltfläche leben. Man kann sich ja die Super-Raumzeit so vorstellen, dass die Grassmann-Variablen jeden Raumzeitpunkt gleichsam wie eine Wolke einhüllen. Die \( \psi^{\mu}(\sigma_{1},\sigma_{2}) \) sind dann die Grassmann-Wolke an jedem Punkt der String-Weltfläche. Aber wie gesagt – nicht zuviel interpretieren. Im Grunde suchen wir nur nach einer supersymmetrischen Erweiterung des String-Wirkungsfunktionals, das auch fermionische (also antikommutierende) Objekte umfasst.
Man baut nun die Fermionfelder (besser: Grassmannkoordinaten) ähnlich ein, wie man das im einfachsten supersymmetrischen Modell (Wess-Zumino-Modell, siehe Kapitel 6.1) tut. Die Koordinaten \( \rho^{\mu} \) der Stringfläche entsprechen dabei den skalaren Feldern des Wess-Zumino-Modells und die Stringparameter \(\sigma_{i}\) entsprechen den Raumzeitkoordinaten \(x^{\mu}\) des Wess-Zumino-Modells. Einen Term wie \[ g(u_{i},u_{i}) = \frac{\partial \rho_{\mu}}{\partial \sigma_{i}} \frac{\partial \rho^{\mu}}{\partial \sigma_{i}} \] (mit Summation über \(\mu\)) in der Wirkung ersetzt man dazu durch einen Term der Form (schematisch) \[ \frac{\partial \rho_{\mu}}{\partial \sigma_{i}} \frac{\partial \rho^{\mu}}{\partial \sigma_{i}} + \psi_{\mu} \, \gamma^{i} \, \frac{\partial \psi^{\mu}}{\partial \sigma_{i}} \] mit geeigneten Matrizen \( \gamma^{i} \) (analog zu den Diracmatrizen).
Solche Terme sind supersymmetrisch, d.h. man kann analog zum Wess-Zumino-Modell eine Transformation zwischen \(\rho_{\mu}\) und \(\psi_{\mu}\) definieren, die diese Terme nicht ändert. Schematisch: \[ \delta \rho^{\mu} \sim \theta \, \psi^{\mu} \] \[ \delta \psi^{\mu} \sim (W \, \rho^{\mu}) \, \theta^{*} \] mit einem geeignet definierten Weyl-Operator \[ W = \gamma^{i} \frac{\partial}{\partial \sigma_{i}} \] der im Wesentlichen eine Ableitung nach den \( \sigma_{i} \) beinhaltet (siehe Kapitel 6.1).
Natürlich muss man nun in eine detaillierte Analyse dieser Theorie einsteigen und sich auch mit der Quantisierung befassen. Man erkennt, dass das bosonische Tachyon verschwindet, d.h. der quantenmechanische Vakuumzustand ist stabil. Außerdem ändert sich die Dimension der Raumzeit, in der die Theorie konsistent ist: Statt 26 Raumzeit-Dimensionen braucht man nun 10 Raumzeit-Dimensionen (eine Zeitdimension und 9 Raumdimensionen).
© Jörg Resag, www.joerg-resag.de
last modified on 13 December 2023