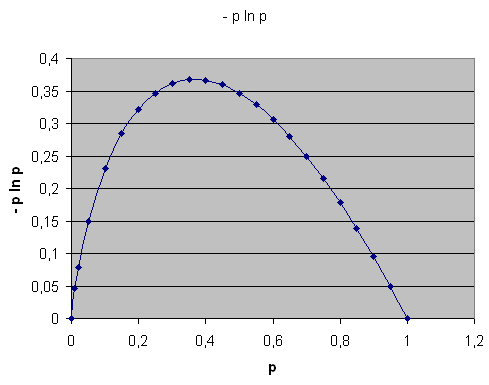
So hängen die Summanden \( - P_{n} \, \ln{ P_{n} } \) in \(S\) von der Wahrscheinlichkeit \( P_n = p \) ab.
Über die Entropie haben wir in Kapitel 1a und Kapitel 1b bereits vieles erfahren. Um den Begriff aber umfassend zu verstehen, muss man ihn sich noch aus einer anderen Perspektive heraus ansehen:
Entropie sagt etwas darüber aus, welche Informationen man über ein System hat, wenn man es durch ein statistisches Ensemble beschreibt, und wieviel Information man haben könnte, wenn man es durch einen Mikrozustand beschreiben könnte. Entropie ist ein Maß für das Informationsdefizit zwischen Makro- und Mikrozustand.
Bevor wir tiefer einsteigen, hier noch eine kurze Wiederholung der wesentlichen Ergebnisse aus Kapitel 1a und Kapitel 1b:
Die Entropie benötigt man zur statistische Beschreibung eines makroskopischen Systems durch Makrozustände, die man durch einige wenige Zustandsgrößen kennzeichnen kann. So kann man beispielsweise einen Behälter mit Wasserstoff im thermischen Gleichgewicht durch die drei Größen Energie \(E\), Volumen \(V\) und Teilchenzahl \(N\) beschreiben, kurz \[ (E, V, N) \]
Zu einem Makrozustand gehören unglaublich viele Mikrozustände, die verschiedene Möglichkeiten darstellen, den Makrozustand mikroskopisch zu realisieren. Quantenmechanisch sind diese Mikrozustände einfach die N-Teilchenzustände (Quanten-Wellenfunktionen) des makroskopischen Systems, die in dem Makrozustand erreichbar sind.
Die Wahrscheinlichkeit, mit der ein Mikrozustand \[ |n \rangle \] in einem bestimmten Makrozustand auftritt, haben wir \[ P_{n} \] genannt. Die Wahrscheinlichkeiten \(P_{n}\) für alle Mikrozustände bilden zusammen das statistische Ensemble (auch statistische Gesamtheit oder Verteilung genannt) für den Makrozustand.
Besonders einfach ist mikrokanonische Ensemble, das gleichsam den Prototyp bildet und aus dem sich die gesamte Thermodynamik ableiten lässt. Der Makrozustand ist dabei durch Energie \(E\), Volumen \(V\) und Teilchenzahl \(N\) gekennzeichnet, wobei man eine (makroskopisch kleine, aber mikroskopisch große) Energieunschärfe \[ \delta E \] zulässt, so dass genügend viele Mikrozustände erreichbar sind. Man spricht hier von einem makroskopisch abgeschlossenen System – das bedeutet, dass die Werte von \(E\) (mit Intervall \(\delta E\)), \(V\) und \(N\) fest vorgegeben sind und die erreichbaren Mikrozustände festlegen, dass es sonst keine weiteren Nebenbedingungen an das Ensemble gibt und dass die geringe Restwechselwirkung mit der Umgebung nur dadurch berücksichtigt wird, dass das System sehr schnell und willkürlich zwischen den erreichbaren Mikrozuständen herumspringt.
Alle erreichbaren Mikrozustände treten dabei mit derselben Wahrscheinlichkeit \[ P_{n} = \frac{1}{\Omega} \] auf, wobei \(\Omega\) die Zahl der erreichbaren Mikrozustände ist (die also im Energieintervall \(\delta E\) liegen). Ein typischer Wert bei \(N = 10^{20}\) Teilchen ist \[ \Omega = 10^{(10^{20})} \] Den natürlichen Logarithmus dieser Zahl, aus historischen Gründen versehen mit der Boltzmannkonstante \(k\) als Vorfaktor, nennt man die Entropie des Makrozustandes:
| Entropie im mikrokanonischen Ensemble (also bei gleichen Zustandswahrscheinlichkeiten \(P_{n} = 1/\Omega\) ): \[ S = k \, \ln{ \Omega} \] |
Damit ist die Entropie proportional zur Zahl der Dezimalstellen von \(\Omega\).
Diese Dezimalstellenzahl ist von der Größenordnung der Teilchenzahl \(N\) und nahezu unabhängig von der Größe des Energieintervalls \(\delta E\), solange \(\delta E\) sehr viel kleiner als \(E\) (→ makroskopisch klein) und sehr viel größer als der Energieabstand benachbarter Mikrozustände (→ mikroskopisch groß) ist.
Da derjenige Makrozustand bei weitem am wahrscheinlichsten ist, der die meisten Realisierungsmöglichkeiten \(\Omega\) aufweist, wird die Entropie im thermischen Gleichgewicht ein Maximum annehmen.
Wenn man \(E, V\) oder \(N\) nicht fest vorgibt, sondern Fluktuationen in einem oder mehreren dieser Werte zulässt und dabei nur den Mittelwert durch ein Wärmebad fixiert, so ergeben sich andere statistische Ensembles.
Beispielsweise kann man eine Temperatur \(T\) vorgeben und dadurch den Mittelwert von \(E\) fixieren. Der Makrozustand und das zugehörige statistische Ensemble (kanonisches Ensemble genannt) werden dann durch \(T, V, N\) beschrieben.
Bei makroskopischen Systemen ist die Schwankungsbreite um die fixierten Mittelwerte sehr klein, so dass die verschiedenen Beschreibungen makroskopisch gleichwertig sind – beispielsweise kann man die mittlere Fluktuation der Energie beim kanonischen Ensemble gleich dem Energieintervall \(\delta E\) des mikrokanonischen Ensembles setzen und damit dann die makroskopische Gleichwertigkeit der beiden Ensembles nachweisen.
Mikroskopisch (beispielsweise in Bezug auf kleine Teilsysteme oder gar einzelne Atome) unterscheiden sich die Beschreibungen jedoch. Das mikrokanonische Ensemble ist nur für makroskopische Systeme sinnvoll, während das kanonische Ensemble (und vergleichbare Ensembles) auch für mikroskopische Teile des Gesamtsystems anwendbar sind, denn man kann den Rest des Systems dann als Wärmebad für das kleine Teilsystem betrachten.
Im Gegensatz zum mikrokanonischen Ensemble sind dann aber die Wahrscheinlichkeiten \(P_{n}\) für die verschiedenen Mikrozustände \( |n \rangle \) nicht mehr gleich groß, so dass die obige – sehr anschauliche – Definition der Entropie nicht mehr anwendbar ist und erweitert werden muss.
Dazu schreibt man die obige Entropie-Definition vom mikrokanonischen Ensemble \( S = k \, \ln{ \Omega } \) zunächst etwas um, indem man \{ P_{n} = P = 1/\Omega =: P \] verwendet: \[ S = k \, \ln{ \Omega } = k \, \ln{ \left( \frac{1}{P} \right) } = - k \, \ln{ P } \] Das funktioniert gut, solange \( P_{n} = P \) unabhängig von \(n\) (also für alle erreichbaren Mikrozustände gleich) ist.
Ist das nicht mehr der Fall, so verallgemeinern wir diese Definition und verwenden statt dem konstanten \(P\) einfach die Wahrscheinlichkeit desjenigen Mikrozustandes, der genau bei den fixierten Mittelwerten liegt. Da bei makroskopischen Systemen die Schwankung um den Mittelwert sowieso sehr klein ist, scheint das eine vernünftige Wahl zu sein.
Wenn wir beispielsweise \(T\) vorgeben und damit den Mittelwert \(E\) fixieren, so schreiben wir \[ S = - k \, \ln{ P(E) } \] Dabei ist im zugehörigen kanonischen Ensemble \[ P(E) = \frac{1}{Z} \, e^{- \frac{E}{kT}} \] und \(E\) ist der fixierte Mittelwert der Energie.
Analog: Wenn wir zusätzlich noch das chemische Potential \(\mu\) vorgeben und damit den Mittelwert der Teilchenzahl \(N\) zusätzlich fixieren, so schreiben wir \[ S = - k \, \ln{ P(E,N) } \] Dabei ist im zugehörigen großkanonischen Ensemble \[ P(E,N) = \frac{1}{Z_{G}} \, e^{ \frac{\mu N - E} {kT}} \] und \(N\) ist der fixierte Mittelwert der Teilchenzahl. Wenn wir \(\mu = 0\) setzen, so kommen wir wieder zum kanonischen Ensemble zurück.
Rechnen wir am Beispiel des großkanonischen Ensembles die Entropie ein wenig um, wobei wir \[ 1 = \sum_{n} \, P_{n} \] \[ E = \sum_{n} \, P_{n} \, E_{n} \] \[ N = \sum_{n} \, P_{n} \, N_{n} \] \[ P_n = \frac{1}{Z_{G}} \, e^{ \frac{\mu N_n - E_n} {kT}} \] verwenden: \[ S = - k \, \ln{ P(E,N) } = \] \[ = - k \, \ln{ \left( \frac{1}{Z_{G}} \, e^{ \frac{\mu N - E} {kT}} \right) } = \] \[ = - k \, \left( \ln{ \left( \frac{1}{Z_{G}} \right) } + \mu \, \frac{N}{kT} - \frac{E}{kT} \right) = \] \[ = - k \, \sum_{n} \, P_{n} \, \left( \ln{ \left( \frac{1}{Z_{G}} \right) } + \mu \, \frac{N_{n}}{kT} - \frac{E_{n}}{kT} \right) = \] \[ = - k \, \sum_{n} \, P_{n} \, \ln { \left( \frac{1}{Z_{G}} \, e^{ \frac{\mu N_{n} - E_{n}} {kT}} \right) } = \] \[ = - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} } \] Die Rechnung lässt sich analog auch für andere fixierte Mittelwerte und zugehörige Ensembles durchführen. Für das kanonische Ensemble muss man nur \(\mu = 0\) in der Rechnung setzen und entsprechend alle Teilchenterme weglassen.
Unsere Idee, einfach statt einem konstanten \(P\) die Wahrscheinlichkeit des Mikrozustandes an den fixierten Mittelwerten zu verwenden, führt also generell zu folgender verallgemeinerter Entropiedefinition:
| Entropie (allgemeine Definition): \[ S = - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} } \] |
Nun ist es zwar schön, dass sich unsere anschaulich leicht zugängliche
Anfangsdefinition
\[ S = k \, \ln{ \Omega } \]
so zwanglos verallgemeinern lässt.
Es wäre aber schön, wenn wir auch die verallgemeinerte
Definition
\[
S = - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} }
\]
direkt anschaulich verstehen könnten.
Außerdem ist nicht mehr unmittelbar klar, warum diese verallgemeinerte Entropie im thermischen Gleichgewicht ein Maximum annehmen soll. Versuchen wir also, eine entsprechende Interpretation für die verallgemeinerte Entropie zu finden.
Anmerkung: Dieser Abschnitt orientiert sich u.a. an M.Stingl: Statistische Mechanik.
Um die obige verallgemeinerte Entropiedefinition zu verstehen, wollen wir uns folgende Idee ansehen:
Wir betrachten ein System A, das sich in einem schwachen Kontakt mit seiner Umgebung A' befindet. Diese Umgebung A' soll sehr groß sein – man kann auch von einem Wärmebad sprechen. Das System A selber muss nicht unbedingt groß sein, aber die Wechselwirkung mit der Umgebung A' muss groß genug sein, so dass sich das System nur sehr kurz in einem Mikrozustand halten kann (sie die Diskussion zur Kohärenzzeit am Ende des vorherigen Kapitels ).
Die unkontrollierte Wechselwirkung mit der großen Umgebung A' führt nun dazu, dass fast jede Information über System A, die wir anfänglich möglicherweise noch besitzen, sehr schnell immer weniger Wert ist. Sie diffundiert gleichsam in die Umgebung A' hinaus und geht verloren (siehe Kapitel 1b: Anhang 2 ).
Schon nach Sekundenbruchteilen können wir uns nur noch auf die Informationen verlassen, die wir aufgrund der experimentellen Anordnung ständig makroskopisch sicherstellen können. Nur diese sicheren Informationen wollen wir zur Beschreibung des Systems im Gleichgewicht verwenden – Stingl spricht vom Grundsatz geringster Voreingenommenheit. Unser statistisches Ensemble soll also keinerlei Zusatzinformation enthalten, die wir nicht wirklich besitzen und sicherstellen können.
Anmerkung:
Der Grundsatz geringster Voreingenommenheit lässt sich nicht allgemein beweisen.
Er stellt eine statistische Grundannahme dar, die plausibel ist, die durch die Erfahrung bestätigt wird
und die in vielen Modellen überprüft werden kann.
Man kann sich aber auch den Fall vorstellen, dass
das System verborgene Informationen besitzt, die wir vielleicht nicht kennen oder
die nur sehr langsam durch die Umgebung verwischt werden – man spricht von metastabilen Systemen.
In diesem Fall gilt es, diese Informationen aufzuspüren und in dem Ensemble zu berücksichtigen.
Wir suchen nun ein Maß für das Informationsdefizit des statistischen Ensembles von A. Nach dem Grundsatz geringster Voreingenommenheit muss dieses Maß im Lauf der Zeit immer mehr anwachsen, bis es im Gleichgewicht maximal wird – genau wie die Entropie.
Starten wir also mit einem statistischen Ensemble (also mit gewissen Wahrscheinlichkeiten \(P_{n}\) für die einzelnen Mikrozustände) von A und nehmen wir an, dass wir keine weitere Information über das System A haben.
Nun führen wir ein Gedankenexperiment durch:
Angenommen, wir könnten ermitteln, in welchem Mikrozustand
\[
|n \rangle
\]
sich unser System A momentan befindet.
Das ist natürlich in der Praxis nicht durchführbar, aber das soll uns hier nicht interessieren
– deshalb ist es ja auch ein Gedankenexperiment.
Wieviel wäre diese neu hinzugewonnene Information über den aktuellen Mikrozustand nun wert, wenn uns zuvor nur die Wahrscheinlichkeiten \(P_{n}\) bekannt waren?
Das wird von diesen Wahrscheinlichkeiten \(P_{n}\) abhängen, mit der die Mikrozustände im Mittel auftreten.
Ist \(P_{n} = 1\) für unseren gefundenen Mikrozustand \(|n \rangle\), d.h. tritt immer nur dieser Mikrozustand auf, dann liefert unsere Messung keine neue Information – das Ergebnis war sowieso klar.
Ist dagegen \(P_{n}\) fast Null und finden wir trotzdem diesen extrem selten auftretenden Zustand \(|n \rangle\), dann ist diese Information viel Wert.
Statt Wert der Information könnte man auch Grad unserer Überraschung oder Neuigkeitswert sagen. Den praktische Wert oder die Bedeutung der Information für den Empfänger betrachten wir hier nicht – insofern ist der obige Informationsbegriff etwas eingeschränkt zu verstehen. Man kann aber durchaus Querbezüge zu anderen Informationsbegriffen herstellen, beispielsweise zur Komplexität – mehr dazu weiter unten.
Bezeichnen wir mit \[ I(P_{n}) \] den Neuigkeitswert der Information (Grad der Überraschung), den mit Wahrscheinlichkeit \(P_{n}\) auftretenden Mikrozustand \( |n \rangle \) tatsächlich zu finden.
Nach unserer Überlegung muss \[ I(1) = 0 \] sein, denn ein sicheres Ergebnis birgt keine Überraschung und keine neue Information.
Je kleiner \(P_{n}\) wird, umso größer ist unsere Überraschung, den Zustand zu finden, und umso größer muss \( I(P_{n}) \) werden.
Nun kommt ein wichtiger Schritt:
Wir möchten \(I\) gerne so konstruieren, dass sich bei mehreren statistisch unabhängigen Messungen die zugehörigen Informationswerte addieren. \(I\) soll in diesem Sinne ein additives Informationsmaß sein.
Stellen wir uns dazu vor, wir schauen zweimal nach und messen einmal den Mikrozustand \( |n \rangle \) und ein anderes mal den Mikrozustand \( |m \rangle \). Dabei sollen sich diese beiden Messungen nicht gegenseitig beeinflussen – unser System soll also kein Gedächtnis haben, das sich die Messung merkt, ganz analog zu einem Würfel. Die Wahrscheinlichkeit für unser kombiniertes Messergebnis ist also gleich dem Produkt \[ P_{n} \cdot P_{m} \] Wir möchten nun, dass der Informationswert für dieses Kombi-Messergebnis gleich der Summe der einzelnen Informationswerte ist: \[ I(P_{n} \cdot P_{m}) = I(P_{n}) + I(P_{m}) \] Damit stellen wir sicher, dass mit jeder neuen Messung der Wert der gesammelten Information über alle Messungen anwächst.
Vorsicht: Diese Information wird nicht im System gespeichert, sondern sie steht alleine in unserem Messprotokoll. Es ist also keine Information über unser System (die steckt alleine in den Wahrscheinlichkeiten \(P_{n}\)), sondern eine Information über unsere Messungen. Hier wird kein System präpariert, denn die Messinformation wird ja sehr schnell durch den Einfluss der Umgebung im System wieder ausradiert.
Die obige Eigenschaft von \(I\) macht auch Sinn, wenn wir die beiden Messungen an zwei verschiedenen statistisch unabhängigen Systemen vornehmen. Der Informationswert der beiden Messungen ist dann gleich dem Informationswert der ersten Messung plus dem Informationswert der zweiten Messungen, was intuitiv sehr sinnvoll erscheint.
Wenn wir die einzelnen Messergebnisse in einer Zeichenkette hintereinander schreiben, so addieren sich die Informationen der einzelnen Zeichen (Messungen), d.h. die Gesamtinformation wächst linear mit der Länge der Zeichenkette – auch das erscheint plausibel.
Mit den obigen Forderungen ist die Funktion \(I\) bis auf einen positiven Normierungsfaktor \(C\) bereits eindeutig festgelegt:
| \[ I(P_{n}) = - C \, \ln{ P_{n} } \] |
Man kann sich auch auf andere Weise klar machen, warum dies ein sinnvolles Maß für
den Neuigkeitswert der Messinformation ist:
Zunächst kennen wir nur die Wahrscheinlichkeit \(P_{n}\), mit dem unser Mikrozustand \( |n \rangle\) bei vielen Messungen im Mittel auftritt. Wir wissen also, dass es im Mittel etwa \(1/P_{n}\) Messungen dauert, bis er das nächste Mal gemessen wird.
Um genau sagen zu können, wann der nächste Treffer auftritt, müssen wir genau angeben, wieviele Versuche es bis dahin dauert. Diese Versuchsanzahl (nennen wir sie \(x\)) ist von der Größenordnung \(1/P_{n}\), d.h. wir brauchen ungefähr \[ \log_{2} { \frac{1}{P_{n}} } = - \log_{2} {P_{n}} \] Bit an Information, um die genaue Versuchsanzahl \(x\) als Binärstring aufzuschreiben und damit unsere statistische Information (Wahrscheinlichkeit \(P_{n}\)) durch eine exakte Information (neuer Treffer nach \(x\) weiteren Versuchen) zu ersetzen. Statt dem Zweierlogarithmus \( \log_{2} \) (Binärlogarithmus) können wir auch den natürlichen Logarithmus mit einem passenden Vorfaktor verwenden, was unser obiges Informationsmaß ergibt.
Recht interessant ist noch die folgende Überlegung, die \( I(P_{n}) \)
mit der algorithmischen Komplexität verknüpft
(hatte ich bei Marriage, Prof. Groth:
Computing Entropy: Understanding Maxwell's Demon, 1998 gefunden;
scheint im Internet nicht mehr verfügbar zu sein).:
Man kann nämlich analog zur Berechnung von Chaitins Zahl \( \Omega \) (die heißt rein zufällig genauso wie unsere Zustandsanzahl oben, siehe auch Die Grenzen der Berechenbarkeit, Kapitel 3.4) die Wahrscheinlichkeit dafür ausrechnen, dass ein immer länger werdender bitweise gewürfelter Binärstring \(p\) irgendwann ein Programm auf einem gegebenen Computer \(U\) darstellt, welches einen bestimmten vorgegebenen String \(s_{n}\) ausgibt und dann anhält (bei Chaitins \(\Omega\) fordert man dagegen nur, dass das Programm überhaupt anhält).
Eine weitere Verlängerung des Programmstrings \(p\) erübrigt sich dann, denn Programme müssen Präfix-frei sein, d.h. jede Verlängerung eines Programmstrings ist selbst kein Programmstring.
Man stößt also beim Verlängern eines Bitstrings mit immer neuen gewürfelten Bits nur maximal einmal auf einen Programmstring, und dieser ist dann einer der \(2^{|p|}\) Bitstrings mit \(|p|\) Bits.
Die Berechnung dieser Wahrscheinlichkeit folgt insgesamt derselben Argumentation wie bei der Berechnung von \(\Omega\) in Die Grenzen der Berechenbarkeit, Kapitel 3.4 mit dem Ergebnis: \[ P(s_{n}) = \sum_{p}' \, \left( \frac{1}{2} \right)^{|p|} = \] \[ = \left( \frac{1}{2} \right)^{|p_{1}|} + \left( \frac{1}{2} \right)^{|p_{2}|} + \, ... \] wobei der Strich an der Summe sagt, dass die Summe über alle Programme \(p\) läuft, die auf der Maschine \(U\) anhalten und den String \(s_{n}\) ausgeben. Dabei ist \(|p|\) die Programmlänge in Bits und \(p_1, p_2, \, ...\) sind die einzelnen entsprechenden Programme (die man ja durchnummerieren kann, was den Index bestimmt).
Picken wir uns den größten Summanden rechts heraus, also den Summanden mit dem kleinsten \(|p_{i}|\) (also das kürzeste Programm \(p_{i}\)). Dann ist \[ P(s_{n}) \ge \left( \frac{1}{2} \right)^{|p_{i}|} \] denn wir haben ja alle anderen Programme rechts weggelassen.
Der Zweier-Logarithmus liefert dann \[ \log_{2} {P(s_{n})} \ge - |p_{i}| \] und somit \[ |p_{i}| \ge - \log_{2} {P(s_{n})} = \] \[ =: - A \, \ln{ P(s_{n})} \] mit \[ \frac{1}{A} = \ln{2} \] Da \(p_{i}\) das kürzeste Programm ist, das \(s_{n}\) ausgibt, ist \( |p_{i}| \) nach Definition die algorithmische Komplexität des Ausgabestrings \(s_{n}\) (siehe Die Grenzen der Berechenbarkeit, Kapitel 3.3). Die obige Gleichung bedeutet also:
| Je kleiner die Wahrscheinlichkeit dafür ist, dass ein gewürfeltes Programm auf einem vorgegebenem Computer einen bestimmten String ausgibt, umso größer ist die Komplexität dieses Strings, d.h. umso weniger gut lässt er sich komprimieren und umso länger ist das kürzeste Programm, das ihn ausgeben kann. |
Anders ausgedrückt:
Komplexe Ausgabestrings brauchen Ausgabeprogramme mit einer großen
Mindestlänge, und die werden entsprechend selten gewürfelt.
Den Zusammenhang zu einem bestimmten statistischen Ensemble kann man nun so herstellen:
Wir stellen uns das statistische Ensemble als einen Computer vor, der bei jeder Messung des Mikrozustandes einen Programm-Binärstring würfelt und als Programm laufen lässt, so dass dieses dann als Messergebnis einen String \(s_{n}\) ausgibt und anhält.
Dieser Ausgabestring \(s_{n}\) repräsentiert dann den gemessenen Mikrozustand \( |n \rangle \) – er könnte beispielsweise die extrem vielen Messwerte enthalten, die man braucht, um diesen Mikrozustand haargenau zu identifizieren.
Die Wahrscheinlichkeit \(P(s_{n})\) für die Ausgabe dieses Strings entspricht also der Wahrscheinlichkeit \(P_{n}\), den Mikrozustand \( |n \rangle \) zu finden.
Nun hängt die Wahrscheinlichkeit \( P(s_{n}) \) für die Ausgabe des Strings \(s_{n}\) bei Zufallsprogrammen natürlich von dem gewählten Computer ab, denn verschiedene Computer interpretieren einen Programm-Binärstring unterschiedlich. Andere Computer führen daher zu anderen Wahrscheinlichkeiten für den Ausgabestring \(s_{n}\).
Wir müssen daher einen Computer wählen, der die Wahrscheinlichkeiten \(P(s_{n})\) gleichsam eingebaut hat und in diesem Sinn das statistische Ensemble und seine \(P_{n}\) repräsentiert.
Die Information über das statistische Ensemble steckt also in dem passend gewählten Computer selbst drin.
Daher braucht man auch einen Computer zur Erzeugung des Strings \(s_{n}\) und kann diesen String nicht einfach direkt würfeln, denn so könnte man die vorgegebenen Wahrscheinlichkeiten \(P(s_{n})\) für die Ausgabe dieses Strings nicht garantieren.
Stattdessen würfelt man die Programme und der gewählte Computer interpretiert diese Programme gerade so, dass dabei die Strings \(s_{n}\) mit denjenigen Wahrscheinlichkeiten \(P(s_{n}) = P_{n}\) ausgegeben werden, die das statistische Ensemble vorgibt. Man spricht daher auch von der bedingten Komplexität des Strings \(s_{n}\), denn sie setzt einen passend gewählten Computer voraus.
Die obige Gleichung besagt damit:
| Die bedingte Komplexität des Strings \(s_{n}\), der den Mikrozustand \( |n \rangle \) beschreibt, ist mindestens so groß wie \[ K \cdot I(P_{n}) \] mit einer positiven Konstanten \(K\) und \[ I(P_{n}) = - C \, \ln{ P_{n} } \] Der Neuigkeitswert \( I(P_{n}) \) liefert also in diesem Sinn einen Mindestwert für die bedingte Komplexität des gemessenen Mikrozustandes \( |n \rangle \). |
Man sieht, wie man zwischen den beiden Informationsmaßen Neuigkeitswert
und Komplexität (Nicht-Komprimierbarkeit) interessante Querbezüge herstellen kann.
Soviel erst einmal dazu.
Wir haben also ein Maß für den Neuigkeitswert der Information gefunden,
bei einer (gedachten) Messung einen bestimmten
Mikrozustand vorfinden.
Dieses Maß ermöglicht es uns nun, ein Maß für das Informationsdefizit aufzustellen, das wir vor unserer Messung haben und das in unserer statistischen Gesamtheit insgesamt steckt, also in allen \(P_{n}\) zusammen: Wir bilden einfach den Mittelwert des Informations-Neuigkeitswertes (Überraschungsgrades) bei einer genauen Enthüllung des aktuellen Mikrozustandes:
| \[ S := \sum_{n} \, P_{n} \, I(P_{n}) = \] \[ = - C \, \sum_{n} \, P_{n} \, \ln{ P_{n} } \] |
Das macht Sinn: Wenn wir ein hohes
Informationsdefizit haben, so hat jede Messung des Mikrozustandes im Mittel einen hohen Informations-Neuwert,
und die Information, dass man gerade diesen oder jenen Mikrozustand angetroffen hat, ist im Durchschnitt
kaum vorhersehbar, also sehr überraschend.
Natürlich setzen wir noch
\[
C = k
\]
so dass sich gerade unsere allgemeine Entropie von oben ergibt.
Schauen wir uns dieses Maß des Informationsdefizits genauer an. Hat es wirklich die gewünschten Eigenschaften?
Betrachten wir dazu zunächst einen einzelnen Summanden \[ - P_{n} \, \ln{ P_{n} } \] als Funktion der Wahrscheinlichkeit \(P_{n}\):

So hängen die Summanden
\(
- P_{n} \, \ln{ P_{n} }
\)
in \(S\) von der Wahrscheinlichkeit \( P_n = p \) ab.
Sowohl bei \( P_{n} = 0 \) als auch bei \( P_{n} = 1 \)
ist der entsprechende Summand Null. Dazwischen ist die Kurve positiv und konkav,
bildet also eine Rechtskurve. Daraus ergeben sich wichtige Eigenschaften von \(S\):
Wenn beispielsweise schon vorher feststeht, in welchem Mikrozustand sich unser System befindet, so haben wir die maximal mögliche Information überhaupt, denn wir kennen einen vollständigen Satz Quantenzahlen des Systems, beispielsweise die Impulse und Spins aller Teilchen. In diesem Fall ist nur ein einziges \(P_{n} = 1\) und alle anderen \(P_{n}\) sind gleich Null. Also sind sämtliche Summanden gleich Null und somit ist auch \( S = 0 \). So sollte es sein, denn wir haben keinerlei Informationsdefizit!
Wenn dagegen im anderen Extremfall alle erreichbaren Mikrozustände gleich wahrscheinlich sind, also \[ P_{n} = P = \frac{1}{\Omega} \] gilt, dann enthalten die \(P_{n}\) keine nützliche Information über die Mikrozustände mehr und unser Informationsdefizit sollte maximal sein. Genau diesen Fall hatten wir oben beim mikrokanonischen Ensemble.
Tatsächlich werden wir weiter unten mit Hilfe der Lagrange-Multiplikator-Methode zeigen, dass \[ S = - k \, \sum_{n} \, \frac{1}{\Omega} \, \ln{ \frac{1}{\Omega} } = \] \[ = k \, \ln{ \Omega } \] der maximal mögliche Wert von \(S\) unter der einzigen Nebenbedingung \[ \sum_{n} \, P_{n} = 1 \] ist (siehe auch beispielsweise M.Stingl: Statistische Mechanik, Kapitel 2.1).
Man kann dieses Ergebnis sogar anschaulich verstehen: Starten wir dazu bei gleich großen \[ P_{n} = \frac{1}{\Omega} \] und picken uns zwei beliebige der identischen Summanden \( - P_{n} \, \ln{ P_{n} } \) heraus (beispielsweise den Ersten und den Zweiten, also \(n=1\) und \(n=2\)).
Nun vergrößern wir das eine \(P_{n}\) ein wenig und verringern das andere \(P_{n}\) um denselben Betrag (die Summe aller \(P_{n}\) muss ja konstant bei Eins bleiben). Der eine Summand wird dadurch größer, der andere kleiner, aber die Schrumpfung des einen Summanden ist immer größer als das Wachstum des anderen Summanden, denn die Kurve \( - P_{n} \, \ln{ P_{n} } \) ist konkav, wie das Bild oben zeigt:
Geht man in dem Bild oben an einer beliebigen Stelle ein festes kleines Stück nach links bzw. rechts, so ist der Abfall bei dem einen Schritt immer größer als Zugewinn bei dem entgegengesetzten Schritt, d.h. die Summe der beiden Summanden schrumpft. Es geht bei einem Schritt mit fester Länge immer weiter nach unten als nach oben.
Man kann sich daher vorstellen, dass die Summe insgesamt den größten Wert annimmt, wenn man die Gesamtwahrscheinlichkeit Eins möglichst gleichmäßig auf alle Einzelwahrscheinlichkeiten \(P_{n}\) aufteilt, d.h. \(S\) wird maximal, wenn alle \(P_{n}\) gleich sind (ihre Summe muss sowieso Eins sein). Weiter unten werden wir das noch explizit nachweisen.
Bei gleichen Wahrscheinlichkeiten für die Mikrozustände zeigt die Formel \[ S = k \,\ln{ \Omega } \] noch eine weiter wichtige Eigenschaft: Das Informationsdefizit steigt, wenn die Zahl der erreichbaren Zustände \(\Omega\) zunimmt, denn dann wird die Auswahl an Mikrozuständen immer größer und unsere Unwissenheit immer gravierender. Wäre dagegen nur ein Zustand erreichbar, also \( \Omega = 1 \), so hätten wir wieder Gewissheit und unser Informationsdefizit wäre Null.
Es kommt noch eine weitere entscheidende Eigenschaft von \(S\) hinzu, die Additivitätseigenschaft. Sie erzwingt den Logarithmus-Term in den Summanden (die bisherigen Eigenschaften hätten auch durch andere konkave Summanden erfüllt werden können).
Genauere Details dazu findet man beispielsweise in M.Stingl: Statistische Mechanik, Kapitel 2.1. Wir wollen hier nur kurz nachrechnen, dass die Entropie \(S_{g}\) für ein System Ag, das aus zwei statistisch unabhängigen Systemen A und A' zusammengesetzt wird, gleich der Summe \(S + S'\) der beiden Einzelentropien dieser Systeme ist:
Die Mikrozustände des Gesamtsystems lassen sich zunächst als Produktzustände \[ |n n' \rangle \] der Mikrozustände von A und A' schreiben. Die Wahrscheinlichkeit \(P_{nn'}\) für diesen Mikrozustand ist dann gleich dem Produkt der Wahrscheinlichkeiten für den Zustand \( |n \rangle \) in A und \( |n' \rangle \) in A', also \[ P_{nn'} = P_{n} \cdot P_{n'} \] denn wir hatten vorausgesetzt, dass die beiden Systeme A und A' statistisch unabhängig sind. Für die Entropie gilt dann: \[ S_{g} = \] \[ = - k \, \sum_{n n'} \, P_{nn'} \, \ln{ P_{nn'} } = \] \[ = - k \, \sum_{n n'} \, P_{n} \, P_{n'} \,\ln{ (P_{n} \, P_{n'}) } = \] \[ = - k \, \sum_{n n'} \, P_{n} \, P_{n'} \, ( \ln{ P_{n} } + \ln{ P_{n'} } ) = \] \[ = - k \, \sum_{n'} \, P_{n'} \cdot \sum_{n} \, P_{n} \, \ln{ P_{n} } + \] \[ - k \, \sum_{n} \, P_{n} \cdot \sum_{n'} \, P_{n'} \, \ln{ P_{n'} } = \] \[ = - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} } - k \, \sum_{n'} \, P_{n'} \, \ln{ P_{n'} } = \] \[ = S + S' \] Hinter der Additivität der Entropie steckt also letztlich die Tatsache, dass wir sie als Mittelwert der additiven Größe \[ I(P_{n}) = - k \, \ln{ P_{n} } \] definiert haben. Die Mittelwertbildung zerstört diese Additivität nicht!
Fassen wir zusammen:
|
Entropie als Maß für ein Informationsdefizit: Wenn ein Mikrozustand \( |n \rangle \) mit der Wahrscheinlichkeit \(P_{n}\) in einem statistischen Ensemble auftritt, so ist \[ I(P_{n}) = - C \, \ln{ P_{n} } \] ein additives Maß für den Neuigkeitswert (Überraschungsgrad) der Information, wenn man bei einer (gedachten) Messung tatsächlich diesen Mikrozustand vorfindet. Der statistische Mittelwert \[ S = \sum_{n} \, P_{n} \, I(P_{n}) = \] \[ = - C \, \sum_{n} \, P_{n} \, \ln{ P_{n} } \] dieses Neuigkeitswertes einer Messung ist dann ein Maß für unser Informationsdefizit, das wir aufgrund der angegebenen Wahrscheinlichkeiten \(P_{n}\) zuvor über das System haben: Je größer dieses Informationsdefizit vor einer (gedachten) Messung des momentanen Mikrozustandes ist, umso größer ist im Mittel der gewonnene Informationswert bei dieser Messung. Setzen wir \(C = k\), so ist \(S\) die Entropie eines statistischen Ensembles. Je größer die Entropie ist, umso weniger Information ist in den Wahrscheinlichkeiten \(P_{n}\) des Ensembles enthalten. |
Diese Sichtweise der Entropie stammt im Wesentlichen von
Claude Elwood Shannon (1916 - 2001)
und entstand etwa um das Jahr 1948 herum im Rahmen seiner Entwicklung der Informationstheorie.
Dabei hatte sich Shannon allerdings nicht mit Mikrozuständen eines makroskopischen Systems beschäftigt, sondern mit der Übertragung von Information durch eine Zeichenkette. Die möglichen Zeichen (z.B. A, B, C, ... ) entsprechen dabei unseren Mikrozuständen, die Zeichenkette entspricht vielen nacheinander durchgeführten Messungen des aktuellen Mikrozustandes (also dem Messprotokoll), \(P_{n}\) ist die Wahrscheinlichkeit für das Auftreten des n-ten Zeichens (z.B. B) in langen Zeichenketten und \(I(P_{n})\) ist der Neuigkeitswert für den Empfänger, wenn dieser das n-te Zeichen in der Zeichenkette vorfindet (wobei ihm die Wahrscheinlichkeit für das Auftreten dieses Zeichens bekannt sein muss).
Den Neuigkeitswert der gesamten Zeichenkette bestimmt man nun, indem man einfach den mittleren Neuigkeitswert der Zeichen in der Zeichenkette bestimmt. Die Reihenfolge der Zeichen in der Zeichenkette wird dabei nicht berücksichtigt, d.h. es geht alleine um den mittleren Überraschungsgrad einzelner Zeichen – insofern haben wir es wieder mit einem eingeschränkten Informationsbegriff zu tun.
Entsprechend spielte bei unseren obigen Überlegungen auch die Reihenfolge der Experimente keine Rolle, denn wir gehen davon aus, dass das System aufgrund der unkontrollierten Wechselwirkung mit seiner Umgebung sowieso kein gutes Gedächtnis hat: Die einzelnen Messungen hinterlassen keine Spuren im System, da solche Spuren durch die unkontrollierte Wechselwirkung mit der Umgebung schnell verwischt werden. Genauso ist es auch bei Shannon: Die Quelle (der Sender) der Zeichenkette wird als gedächtnislos angenommen (siehe beispielsweise Wikipedia: Entropie (Informationstheorie) ).
Machen wir uns einen wichtigen Punkt noch einmal klar: Die Entropie ist kein Maß für eine vorhandene Information, sondern für eine Information, die man im Mittel durch eine Messung des Mikrozustandes oder durch ein neu eintreffendes Zeichen noch hinzugewinnen kann – man spricht auch von einem Maß für eine potentielle Information.
In diesem Sinne ist Entropie ein Maß für eine beseitigbare Ungewissheit (also ein Informationsdefizit), die wir vor den Messungen bzw. dem Eintreffen der Zeichen haben. Sie misst die Informationsmenge, die notwendig ist, um durch Messungen oder Angabe von Zeichen die Ungewissheit zu beseitigen.
Besonders deutlich wird dies bei gleichen Wahrscheinlichkeiten \(P_{n} = 1/\Omega\), denn dann ist die Entropie proportional zur Stellenanzahl der Zahl der Mikrozustände. Schreibt man \(\Omega\) im Binärsystem auf und verwendet den Zweierlogarithmus, so ist die Entropie proportional zur Bitanzahl von \(\Omega\). Genau so viele Bits an Information braucht man in diesem Fall maximaler Unwissenheit, um festzulegen, in welchem Mikrozustand sich das System befindet und damit die Ungewissheit über den Mikrozustand zu beseitigen.
In Peter Hägele: Was hat Entropie mit Information zu tun? habe ich folgende schöne Formulierung gefunden, die wohl von C.F.v.Weizsäcker stammt:
|
Entropie gibt also das Informationsdefizit an, das man eingeht, wenn man das System nur durch
seinen Makrozustand beschreibt, anstatt die vollständige Information des Mikrozustandes anzugeben.
Bei makroskopischen Systemen prägt sich allerdings der Informationsgewinn einer Mikrozustands-Messung
nicht im System ein, anders als bei isolierten mikroskopischen Systemen, bei denen sich ein Quantenzustand
präparieren lässt. Die gemessene Information verschwindet unkontrolliert in der Umgebung
des Systems (Stichwort Dekohärenz)
und bereits sehr kurz nach der Messung wissen wir über das makroskopische System wieder so wenig wie
zuvor. Daher bleibt uns gar nichts anderes übrig, als auf die Angabe eines Mikrozustandes zu
verzichten und uns mit der Beschreibung durch einen Makrozustand zufrieden zu geben.
Die Entropie sagt uns dabei, wie groß unser Informationsdefizit ist.
Vorsichtig muss man bei der Vorstellung sein, Entropie sei ein Maß für eine vorhandene Information. Hier muss man genauer sagen: Entropie ist ein Maß für die in einem Mikrozustand im Prinzip vorhandene Information, die uns bei einer viel informationsärmeren Beschreibung durch einen Makrozustand (ein statistisches Ensemble) aber fehlt.
Das Anwachsen der Entropie mit der Zeit bedeutet, dass unsere Beschreibung des Systems durch einen sich wandelnden Makrozustand mit extrem großer Wahrscheinlichkeit immer informationsärmer wird. Information geht durch die Wechselwirkung mit der Umgebung verloren, bis nur noch sehr wenige Informationen sicher sind, beispielsweise die mittlere Energie. Hat man zu Beginn möglicherweise noch eine räumliche Energieverteilung, so hat man im Gleichgewicht nur noch eine überall gleiche mittlere Energiedichte pro Teilchen.
Es gibt noch eine anderen interessanten Zugang zur Entropie als Maß für ein Informationsdefizit, der eng mit unseren obigen Überlegungen zusammenhängt.
Dazu schauen wir uns eine extrem lange Reihe von wiederholten Messungen des Mikrozustandes bei unserem statistischen Ensemble an. Diese Messreihe enthält sehr viele detaillierte Informationen. So sagt sie beispielsweise, dass in Messung Nummer 74357845168265233197... der Mikrozustand Nummer 64534527373278128192390...... gemessen wurde.
Mit sehr großer Wahrscheinlichkeit haben wir es außerdem mit einer typischen Messreihe zu tun, d.h. aus den Häufigkeiten der Messwerte können wir mit hoher Genauigkeit die Wahrscheinlichkeiten \(P_{n}\) für das Auftreten des n-ten Mikrozustandes im statistischen Ensemble ablesen. Nur solche typischen Messreihen wollen wir hier betrachten, d.h. die extrem seltenen untypischen Messreihen ignorieren wir einfach.
Die Frage ist nun: Wieviel Information verlieren wir, wenn uns die Reihenfolge der Messwerte in einer typischen Messreihe überhaupt nicht mehr interessiert? Wir werfen also alle Informationen über die Reihenfolge der Messwerte weg und behalten nur die Information darüber, wie häufig sie auftreten, d.h. wir behalten nur noch die Information über die Wahrscheinlichkeiten \(P_{n}\). Das ist genau der Übergang zu unserem statistischen Ensemble.
Es geht also darum, abzuzählen, wieviele Sortierungsmöglichkeiten der Messergebnisse bei einer typischen Messreihe möglich sind, ohne dass man ihre Häufigkeit ändert.
Bei \(m\) Messungen sind das \[ m! = m \cdot (m - 1) \cdot (m - 2) \cdot \, ... \cdot 1 \] Sortierungsmöglichkeiten. Dabei hat man allerdings auch das Umsortieren identischer Messergebnisse mitgezählt, was man noch korrigieren muss. Tritt beispielsweise der Mikrozustand \(n\) bei \(m_{n}\) Messungen auf, so hat man es mit \( m_{n}! \) Sortierungsmöglichkeiten zu tun, die nur identische Messergebnisse austauschen und die daher nicht unterschieden werden können. Insgesamt gibt es also \[ \frac{m!}{m_{1}! \, m_{2}! \, ... \, m_{\Omega}! } \] verschiedene Sortierungsmöglichkeiten der Messergebnisse, wobei \(\Omega\) die Gesamtzahl der erreichbaren Mikrozustände ist.
Wir wollen den Grenzfall extrem vieler Messungen betrachten, d.h. \(m\) und alle \(m_{n}\) sollen sehr große Zahlen sein – die Zahl der Messungen muss also weit größer als die Zahl der Mikrozustände sein.
Für große Zahlen (etwa ab 1000) kann man den Logarithmus der Fakultät gut durch die Stirlingformel abschätzen: \[ \ln{(m!)} = m \, \ln{m} - m \] Für den Logarithmus der Anzahl Sortierungsmöglichkeiten der Messergebnisse haben wir dann bei sehr vielen Messungen und einer typischen Messreihe (wobei wir \[ \sum_{n} \, m_{n} = m \] \[ \frac{m_{n}}{m} = P_{n} \] verwenden; \(m\) war ja die Gesamtzahl der Messungen und \(m_n\) war die Zahl der Messungen, bei denen der Mikrozustand \(n\) gemessen wurde): \[ \ln{ \left( \frac{m!} {m_{1}! \, m_{2}! \, ... \, m_{\Omega}! } \right) } = \] \[ = \ln {(m!)} - \sum_{n} \, \ln{ (m_{n}!) } = \] \[ = m \, \ln{m} - m - \sum_{n} \, (m_{n} \, \ln{m_{n}} - m_{n}) = \] \[ = m \, \ln{m} - \sum_{n} \, m_{n} \, \ln{ m_{n} } = \] \[ = \sum_{n} \, m_{n} \, (\ln {m} - \ln{ m_{n} } ) = \] \[ = m \, \sum_{n} \, \frac{m_{n}}{m} \, \ln { \frac{m}{m_{n}} } = \] \[ = - m \, \sum_{n} \, P_{n} \, \ln{ P_{n} } = \] \[ = m \, \frac{S}{k} \] Dabei haben wir unsere Entropiedefinition \[ S = - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} } \] verwendet. Halten wir also fest:
|
Entropie als Maß für die Unkenntnis der genauen Reihenfolge
von Messergebnissen in einer typischen Messreihe: Wir betrachten ein statistisches Ensemble mit Wahrscheinlichkeiten \(P_{n}\) für die Mikrozustände. Nun bestimmen wir \(m\)-mal den Mikrozustand, wobei \(m\) eine sehr große Zahl ist (weit größer als die Zahl der Mikrozustände). Mit sehr großer Wahrscheinlichkeit haben wir dann eine typische Messreihe vor uns, d.h. die Häufigkeiten für die Messwerte entsprechen den gegebenen Wahrscheinlichkeiten. Für eine solche typische Messreihe gilt: Die Anzahl Messreihen, die dieselben typischen Häufigkeiten für die Mikrozustände aufweisen (wobei die Reihenfolge, in der einzelnen Mikrozustände in den Messungen auftreten, egal ist), ist von der Größenordnung \[ e^{m \, \frac{S}{k}} \] mit der Entropie \[ S = - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} } \] Der Ausdruck ist von der Größenordnung bedeutet dabei, dass der Logarithmus der betrachteten Messreihenanzahl bei sehr langen Messreihen in sehr guter Näherung durch \(m \, S/k \) gegeben ist. Wir können also die Stellenzahl der Messreihenanzahl sehr genau aus der Entropie berechnen, nicht aber den genauen Wert der Zahl selbst. Mit sehr guter Genauigkeit gilt aber die folgende Aussage für lange typische Messreihen: Mit jeder neuen Messung wächst die Zahl der typischen Messreihen mit vorgegebenen typischen Häufigkeiten im Mittel um den Faktor \( e^{S/k} \) an.
|
Etwas ungünstig ist dabei noch die Voraussetzung, dass man die Häufigkeiten fest vorgeben muss, also
nur Messreihen mit exakt denselben typischen Häufigkeiten betrachtet.
Was ist mit anderen typischen Messreihen, die ähnliche Häufigkeiten für die Messwerte aufweisen und für die ebenfalls in guter Näherung \( m_{n}/m = P_{n} \) gilt?
Nimmt man alle diese Messreihen mit solchen typischen Häufigkeiten für die Messwerte hinzu, so vergrößert sich die Anzahl der Messreihen zunächst natürlich beträchtlich. Aber: Die Stellenzahl dieser Anzahl (also der Logarithmus) verändert sich dabei nur wenig.
Das liegt daran, dass die Stellenzahl sehr groß ist, so dass einige Stellen mehr oder weniger nicht auffallen. Es ist ganz ähnlich zu unserer Diskussion des Energieintervalls \(\delta E\) beim mikrokanonischen Ensemble im Kapitel 1a:
Auch dort verändert sich die Zustandsanzahl \(\Omega\) natürlich proportional zu \(\delta E\), aber der Logarithmus und damit die Entropie merkt davon fast nichts, solange \(\delta E\) sich nur in einem bestimmten Rahmen ändert.
In unserem Fall wird die Rolle von \(E\) nun von den Häufigkeiten \(m_{n}\) übernommen. Diese sollen typisch bleiben, müssen also für große \(m\) ungefähr durch \( m_{n}/m = P_{n} \) gegeben sein.
Aus der Statistik wissen wir, dass Abweichungen der Häufigkeiten meist nicht größer als deren Wurzel sind. Statt einer Messreihe mit festem \( m_{n} \) könnten wir also \( \sqrt{m_{n}} \)-viele Messreihen mit typischem \( m_{n} \) betrachten.
Wenn wir also die typischen Häufigkeiten \(m_{n}\) nicht fest vorgeben wollen, sondern alle typischen Häufigkeiten zulassen wollen, so müssen wir unsere oben berechnete Anzahl mit dem Faktor \[ \sqrt{m_{1} \, m_{2} \, ... \, m_{\Omega}} \] multiplizieren. Für den Logarithmus ergibt das den Zusatzterm \[ \frac{1}{2} \, \sum_{n} \ln{ m_{n} } \] der gegenüber Termen wie \[ m \, \ln{m} \] oder \[ m_{n} \, \ln{ m_{n} } \] vollkommen vernachlässigbar ist (\(m\) und die \(m_{n}\) sind ja sehr große Zahlen, denn wir betrachten entsprechend lange Messreihen).
Wir können also in den Formulierungen oben einfach von der Anzahl typischer Messreihen sprechen, wobei typische Messreihen dadurch definiert sind, dass die relativen Häufigkeiten recht genau durch die Wahrscheinlichkeiten des statistischen Ensembles gegeben sind. Statistisch ist fast jede beim gegebenen Ensemble gemessene Messreihe eine solche typische Messreihe.
In diesem Sinn kann man \(S\) als Maß für das Informationsdefizit des statistischen Ensembles ansehen: Je größer \(S\) ist, umso weniger weiß man im Voraus über die Details einer auftretenden typischen Messreihe, denn umso mehr typische Messreihen gibt es mit jeder neuen Messung, und umso mehr neue Information gewinnt man also im Mittel bei einer neuen Messung. Diese Aussage gibt der Entropie als Maß für das Informationsdefizit eine ganz konkrete statistische Bedeutung. Schauen wir uns zur Verdeutlichung die beiden Extremfälle an:
Im Extremfall des mikrokanonischen Ensembles ist \( P_{n} = 1/\Omega \) und damit \( e^{S/k} = \Omega \), d.h. mit jeder Messung nimmt die Zahl der typischen Messreihen um den Faktor \(\Omega\) zu. Das ist die maximal mögliche Zunahme, denn hier ist fast jede im Prinzip mögliche Messreihe zugleich eine typische Messreihe: In der Menge aller prinzipiell möglichen Messreihen treten bei den allermeisten dieser Messreihen alle Mikrozustände mit annähernd gleicher Häufigkeit auf, sobald die Messreihe lang genug wird. Wenn aber praktisch alle Messreihen auch typisch sind, dann enthält das statistische Ensemble nur eine minimale Information, denn man kann keine deutlich kleinere Untergruppe der Messreihen als typisch kennzeichnen.
Im anderen Extremfall, bei dem sich das System in einem festen Mikrozustand befindet, ist \( S = 0 \) und \( e^{S/k} = 1 \). Die Zahl der typischen Messreihen wächst also nicht bei weiteren Messungen, denn es gibt nur eine einzige typische Messreihe: Diejenige, bei der das System ständig im selben Mikrozustand vorgefunden wird.
Anmerkung:
Die obigen Formeln kann man auch gut dazu verwenden, um die Entropie eines mikrokanonischen Ensembles direkt durch die mittleren Besetzungszahlen der Einteilchenniveaus auszudrücken. Das ergibt beispielsweise einen alternativen Zugang zu den idealen Quantengasen aus Kapitel 1b. Dazu muss man in den obigen Formeln nur die folgenden Ersetzungen machen:
Übrigens kann man hier bei \(\Omega\) auch von den typischerweise erreichbaren Mikrozuständen sprechen, analog zu den typischerweise auftretenden Messreihen. Das sind demnach die Mikrozustände, bei denen die Besetzungszahlen gut den vorgegebenen Wahrscheinlichkeiten entsprechen. Für die Entropie des mikrokanonischen Ensembles aus \(N\) Teilchen ergibt die obige Rechnung dann: \[ S = k \, \ln{ \Omega } = \] \[ = - k \, N \, \sum_{\boldsymbol{p},\sigma} \, \frac{n(\boldsymbol{p},\sigma)}{N} \, \ln { \frac{n(\boldsymbol{p},\sigma)}{N} } = \] \[ = - k \, N \, \sum_{\boldsymbol{p},\sigma} \, P(\boldsymbol{p},\sigma) \, \ln{ P(\boldsymbol{p},\sigma) } = \] \[ =: N \, S_{Teilchen} \] Dabei ist \[ S_{Teilchen} := - k \, \sum_{\boldsymbol{p},\sigma} \, P(\boldsymbol{p},\sigma) \, \ln{ P(\boldsymbol{p},\sigma) } \] die Entropie für ein einzelnes Teilchen, das sich mit der Wahrscheinlichkeit \( P(\boldsymbol{p},\sigma) \) im Einteilchenzustand \( |\boldsymbol{p},\sigma \rangle \) befindet.
Wir sehen:
Wenn wir die Additivität der Entropie für statistisch unabhängige Teilsysteme
(Teilchen) sicherstellen wollen, so ergibt sich automatisch wieder Shannons Entropieformel (diesmal
für die Teilsysteme, also die einzelnen Teilchen). Die Gesamtentropie \( S = k \ln{ \Omega } \)
des mikrokanonischen Gesamtensembles
wird dann maximal, wenn Shannons Entropie für die einzelnen Teilchen maximal wird.
Die Wahrscheinlichkeiten werden dabei meist durch irgendwelche Nebenbedingungen vorgegeben,
beispielsweise durch einen vorgegebenen Energiemittelwert – wir kommen gleich darauf zurück.
Übrigens:
Die obige Formel
\[
S =
N \, S_{Teilchen}
\]
passt recht gut zu unserer Formel
\[
S = k \, \ln{ \Omega(E) } =
\]
\[
= N \, k \, \ln{ \varphi(\epsilon) }
\]
aus Kapitel 1a ("Der Logarithmus der Zustandszahl"), mit der
wir \( \ln{ \Omega(E) } \) grob abgeschätzt haben.
Dabei war \( \varphi(\epsilon)\) die Zahl der Einteilchenzustände bis zur
Einteilchenenergie \( \epsilon = E/N \), d.h.
\[
k \, \ln{ \varphi(\epsilon) }
\]
können wir grob als
Einteilchen-Entropie ansehen. Unsere damalige Abschätzung wird damit recht gut bestätigt.
Anmerkung: Dieser Abschnitt orientiert sich u.a. an M.Stingl: Statistische Mechanik, Kapitel 3.
Wir haben nun alle Mittel in der Hand, um unter sehr allgemeinen Voraussetzungen die entsprechenden statistischen Ensembles für ein System im thermischen Gleichgewicht zu bestimmen. Dabei lassen wir uns vom Grundsatz geringster Voreingenommenheit leiten: Im thermischen Gleichgewicht soll das statistische Ensemble nur die Informationen beinhalten, die wir über das System haben oder die wir vorgeben und die gegen Einflüsse von außen stabil sind. Alle anderen Informationen werden im thermischen Gleichgewicht durch die Wechselwirkung mit der Umgebung verwischt.
Unser statistisches Ensemble soll also so informationsarm wie nur möglich sein. Mittlerweile wissen wir, dass demnach die Entropie so groß wie nur möglich sein muss, denn die Entropie misst gerade dieses Informationsdefizit. Wir suchen also das Maximum für die Entropie, um den thermodynamischen Gleichgewichtszustand zu finden, wobei bestimmte Nebenbedingungen sicherstellen, dass vorhandene stabile Informationen verfügbar bleiben.
Natürlich müssen die vorhandenen Informationen dabei sicherstellen, dass die Entropiesumme \[ S = - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} } \] auch konvergiert und ein passendes Maximum einnimmt. Es macht also keinen Sinn, eine unendliche Energiequelle zur Verfügung zu stellen und das Maximum der Entropie für beliebig große Energie zu suchen.
Schauen wir uns den typischen Fall eines makroskopisch isolierten Systems an, bei dem sich \(N\) identische Teilchen in einem Volumen \(V\) befinden und die Gesamtenergie auf ein makroskopisch kleines Intervall zwischen \(E\) und \(E + \delta E\) eingeschränkt ist. Das sind unsere kompletten vorhandenen Informationen.
In diesem Fall legen \(N\) und \(V\) die Mikrozustände fest und das Energieintervall sorgt dafür, dass nur endlich viele Zustände erreichbar sind. Die Entropiesumme hat dann nur endlich viele Summanden, konvergiert also immer.
Gesucht sind nun für das thermische Gleichgewicht diejenigen Werte für \(P_{n}\), für die die Entropie maximal wird. Dabei muss die Nebenbedingung eingehalten werden, dass die Summe aller Wahrscheinlichkeiten \(P_{n}\) über die erreichbaren Zustände gleich Eins ist. Diese Summe können wir auch als Mittelwert des Eins-Operators auffassen. Das Ergebnis wird das mikrokanonische Ensemble sein, aber das werden wir unten noch nachrechnen.
Wir haben in Kapitel 1b weitere Situationen kennengelernt: Hier werden \(E, V, N\) nicht mehr alle scharf vorgegeben wie bei einem streng isolierten System, sondern man lässt Fluktuationen in einer oder mehrerer dieser Größen zu und fixiert nur den entsprechenden Mittelwert durch Kontakt mit einem Wärmebad. Makroskopisch ergeben sich so dieselben Eigenschaften wie bei fest vorgegebenen Werten, da die Fluktuationen im Mittel sehr klein sind, aber das statistische Ensemble, das diese Situation beschreibt, ist ein anderes.
Wir wollen uns hier diese Situationen ganz allgemein anschauen: Die fest vorgegebenen Informationen legen dabei zunächst die erreichbaren Mikrozustände fest. Hinzu kommen ein oder mehrere vorgegebene Mittelwerte – im einfachsten Fall der Mittelwert des Einsoperators, um die Summe aller Wahrscheinlichkeiten \(P_{n}\) auf Eins zu setzen. Das statistische Ensemble mit dem größten Informationsdefizit ist nun dasjenige, bei dem die Entropie maximal wird, wobei die vorgegebenen Mittelwerte als Nebenbedingungen wirken.
Die Mittelwerte sollen zeitlich konstant sein, denn wir wollen mit ihnen ja vorliegende stabile Informationen über einen Gleichgewichtszustand beschreiben. Diese Mittelwerte gehören also zu quantenmechanischen Observablen \( \hat{A}_{i} \), die mit dem Hamiltonoperator des Systems vertauschen. Die Mikrozustände können wir dann zugleich als Eigenvektoren des Hamiltonoperators und dieser Mittelwert-Observablen wählen. Der statistische Charakter dieser Observablen entsteht dann alleine durch die Wahrscheinlichkeiten \(P_{n}\) des Ensembles und nicht durch die quantenmechanische Unschärferelation.
Insgesamt ergibt sich damit die folgende Maximierungsaufgabe mit Nebenbedingungen:
|
Bestimmung des statistischen Ensembles im Gleichgewicht: Wähle bei gegebenen Mikrozuständen \( |n \rangle \) deren Wahrscheinlichkeiten \(P_{n}\) im statistischen Ensemble so, dass die Entropie \[ S = - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} } \] maximal wird, wobei die folgenden \(I+1\) Nebenbedingungen gelten: \[ a_{i} = \langle \hat{A}_{i} \rangle = \sum_{n} \, P_{n} \, (a_{i})_{n} \] (mit \(i\) von \(0\) bis \(I\)). Dabei sind \[ a_{i} = \langle \hat{A}_{i} \rangle \] die \(I+1\) Mittelwerte, die vorgegeben sind (beispielsweise durch ein äußeres Wärmebad) und \[ (a_{i})_{n} \] ist der Eigenwert (Messwert) der Observablen \( \hat{A}_{i} \) bei dem n-ten Mikrozustand. Die immer notwendige Normierungsbedingung für die Wahrscheinlichkeiten berücksichtigen wir durch die nullte Nebenbedingung, indem wir \( \hat{A}_0 = \hat{1} \) setzen (d.h. für alle \(n\) ist \( (a_{0})_{n} = 1 \)) und \( a_{0} = 1 \) fordern. Die nullte (\(i=0\)) Nebenbedingung lautet also \[ 1 = \langle \hat{1} \rangle = \sum_{n} \, P_{n} \] |
Man kann die Nebenbedingungen über die bekannte Methode
der Lagrange-Multiplikatoren berücksichtigen,
indem man statt der Funktion \(S\) die neue Funktion
\[
S - \sum_{i} \, \lambda_{i} \, \langle \hat{A}_{i} \rangle
\]
in den Variablen \(P_{i}\) maximiert und anschließend die neu eingeführten reellen Parameter
(Lagrange-Multiplikatoren) \( \lambda_{i} \) so anpasst,
dass die Nebenbedingungen erfüllt sind. Warum das funktioniert, wird sehr schön
in Wikipedia: Lagrange-Multiplikator
erklärt. Hier ist meine Version davon:
Im \(\Omega\)-dimensionalen Variablenraum der \( P_{n} \) können wir verallgemeinerte Höhenlinien von \( S \) und den einzelnen \( \langle \hat{A}_{i} \rangle \) einzeichnen.
Diese verallgemeinerten Höhenlinien haben eine Dimension weniger als der Variablenraum der \(P_{n}\), sind also keine eigentlichen Linien, sondern \((\Omega - 1)\)-dimensionale Unterräume des Variablenraums, in denen jeweils \(S\) oder ein \( \langle \hat{A}_{i} \rangle \) konstant ist.
Es gibt demnach in jedem Punkt einer Höhenlinie genau eine Richtung im Variablenraum, die senkrecht auf dieser Höhenlinie steht. Man spricht auch von dem Normalenvektor der Höhenlinie. Dieser Normalenvektor ist gleich dem Gradienten der Funktion, die auf der Höhenlinie konstant ist.
Um eine Nebenbedingung einzuhalten, müssen wir im \(P_n\)-Variablenraum nun auf ihrer Höhenlinie entlangwandern, nämlich auf der mit dem vorgegebenen Wert für die Nebenbedingungsfunktion \[ a_{i} = \langle \hat{A}_{i} \rangle = \sum_{n} \, P_{n} \, (a_{i})_{n} \] Da wir alle \(I+1\) Nebenbedingungen zugleich einhalten wollen, wandern wir entsprechend auf der gemeinsamen Schnittlinie aller \(I+1\) Höhenlinien entlang, denn nur dort gelten alle Nebenbedingungen zugleich.
Diese Schnittlinie hat bei \(I+1\) Nebenbedingungen auch \(I+1\) weniger Dimensionen als der \(P_{n}\)-Variablenraum, in dem sie liegt. Die Richtungen senkrecht zu dieser Schnittline lassen sich als Linearkombination der \(I+1\) Gradientenvektoren (Normalenvektoren) zu den \( \langle \hat{A}_{i} \rangle \)-Nebenbedingungsfunktionen schreiben.
Bei dem Entlangwandern entlang der Schnittlinie aller Nebenbedingungen überschreiten wir nun normalerweise Höhenlinien von \(S\), d.h. \(S\) schrumpft oder wächst auf unserer Wanderung durch das \(S\)-Gebirge im \(P_n\)-Variablenraum.
Ein Maximum (oder Minimum oder Sattelpunkt) von \(S\) auf der Nebenbedingungs-Schnittline erreichen wir dann, wenn der \(S\)-Gradientenvektor genau senkrecht zu unserer Schnittline zeigt. Unser Weg verläuft an dieser Stelle auf einem Abhang von \(S\), ohne dass wir im \(S\)-Gebirge auf- oder absteigen. Nach oben oder unten (also in Richtung des Gradienten von \(S\)) geht es nur senkrecht zu unserer Schnittlinie, und diese Richtungen können wir ja als Linearkombination der \(I+1\) Gradientenvektoren (Normalenvektoren) unserer \( \langle \hat{A}_{i} \rangle \)-Nebenbedingungsfunktionen schreiben: \[ \frac{\partial S}{\partial P_{n}} = \sum_{i} \, \lambda_{i} \, \frac{\partial \langle\hat{A}_{i} \rangle}{\partial P_{n}} \]
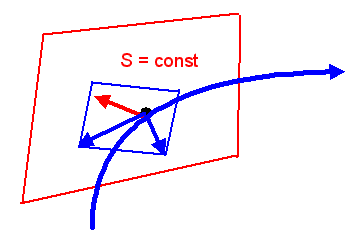
In diesem Beispiel für die Maximierung mit Nebenbedingungen ist der
Variablenraum der \( P_{n} \) dreidimensional und es gelten
zwei Nebenbedingungen. Die blaue eindimensionale Kurve repräsentiert diejenigen \( P_{n} \),
die diese beiden Nebenbedingungen zugleich erfüllen.
Die Entropie \(S\) nimmt nach hinten links zu.
Im schwarzen Punkt streift die blaue Nebenbedingungslinie eine
Höhenfläche mit konstantem \(S\) (rot eingezeichnet), d.h. hier liegt
der Punkt, wo die blaue Linie das dort maximal mögliche \(S\) besitzt.
Der Gradient von \(S\) (also die Richtung mit der
stärksten Entropiezunahme, dargestellt durch den roten Pfeil) steht an diesem Punkt
senkrecht auf der blauen Linie.
Da nun die blaue Linie die Schnittlinie zweier Nebenbedingungs-Flächen mit jeweils konstantem
\( \langle \hat{A}_{1} \rangle \)
bzw. \( \langle \hat{A}_{2} \rangle \) ist
(nicht eingezeichnet), wird die Ebene senkrecht zu der blauen
Linie (blau eingezeichnete Fläche) von den Normalenvektoren
(blaue Pfeile) dieser beiden Nebenbedingungs-Flächen in diesem Punkt aufgespannt.
In dieser Ebene muss der Gradient von \(S\)
(roter Pfeil) liegen, denn auch dieser steht senkrecht zur blauen Linie.
Die beiden blauen Normalenvektoren sind nun zugleich die
Gradienten von \( \langle \hat{A}_{1} \rangle \)
und \( \langle \hat{A}_{2} \rangle \).
Der Gradient von \(S\) im Berührungspunkt ist also eine Linearkombination dieser beiden
Gradienten.
Diese Gleichung gilt für alle Werte von \(n\), also für alle Komponenten des Gradientenvektors,
und wir erhalten sie, indem wir das Maximum
der obigen Funktion
\[
S - \sum_{i} \, \lambda_{i} \,\langle \hat{A}_{i} \rangle
\]
suchen,
also deren Gradient gleich Null setzen:
\[
\frac{\partial}{\partial P_{n}} \,
\left(
S - \sum_{i} \, \lambda_{i}
\langle \hat{A}_{i} \rangle \right)
= 0
\]
Das ergibt wegen der Linearität der Ableitung genau unsere Gleichung
\[
\frac{\partial S}{\partial P_{n}} = \sum_{i} \, \lambda_{i} \,
\frac{\partial \langle\hat{A}_{i} \rangle}{\partial P_{n}}
\]
von oben.
Die Lösungswerte \(P_{n}\) dieser Gleichung hängen von den Lagrange-Multiplikatoren \( \lambda_{i} \) ab. Die genauen \( \lambda_{i} \)-Werte sind dann durch die Nebenbedingungen \[ a_{i} = \langle \hat{A}_{i} \rangle \] mit den vorgegebenen \(a_i\)-Werten festgelegt (denn die \(P_n\) in der Nebenbedingungsfunktion \(\langle \hat{A}_{i} \rangle\) hängen ja von den \( \lambda_{i} \) ab).
Setzen wir die genaue Form der Funktionen \(S\) und \( \langle\hat{A}_{i} \rangle \) ein und werten wir die obige Gleichung aus: \[ \frac{\partial}{\partial P_{n}} \, \bigg( - k \, \sum_{n'} \, P_{n'} \, \ln{ P_{n'} } + \] \[ - \sum_{i} \, \lambda_{i} \, \sum_{n'} \, P_{n'} (a_{i})_{n'} \bigg) = 0 \] \[ \Longleftrightarrow \] \[ k \, \ln{ P_{n} } + k \, P_{n} \, \frac{1}{P_{n}} + \sum_{i} \, \lambda_{i} \, (a_{i})_{n} = 0 \] \[ \Longleftrightarrow \] \[ \ln{ P_{n} } = - \left( 1 + \sum_{i} \, \frac{\lambda_{i}}{k} \, (a_{i})_{n} \right) \] \[ \Longleftrightarrow \] \[ P_{n} = e^{ - \left( 1 + \sum_{i} \, \frac{\lambda_{i}}{k} \, (a_{i})_{n} \right) } \] Es macht Sinn, die Nullte Nebenbedingung explizit auszuwerten, denn sie gilt universell. Wir nehmen also den Summanden für \( i = 0 \) aus der Summe \( \sum_i \) heraus und schreiben ihn aus, wobei wir \( (a_{0})_{n} = 1 \) verwenden: \[ P_{n} = e^{ - \left( 1 + \frac{\lambda_{0}}{k} + \sum_{i=1}^{I} \, \frac{\lambda_{i}}{k} \, (a_{i})_{n} \right) } \] Um an die übliche Schreibweise anzuknüpfen, setzen wir \[ e^{- \left( 1 + \frac{\lambda_{0}}{k} \right) } =: \frac{1}{Z} \] und nennen \(Z\) die generalisierte Zustandssumme. Sie ist durch die Nullte Nebenbedingung bestimmt, also durch die Normierungsbedingung, dass die Summe aller \(P_{n}\) gleich Eins sein muss. Damit haben wir:
|
Das allgemein-kanonische Ensemble: Bei vorgegebenen konstanten Mittelwerten maximiert das folgende allgemein-kanonische Ensemble die Entropie: \[ P_{n} = \frac{1}{Z} \, e^{ - \sum_{i=1}^{I} \, \frac{\lambda_{i}}{k} \, (a_{i})_{n} } \] Dabei ist die generalisierte Zustandssumme \(Z\) als Wahrscheinlichkeits-Normierungsfaktor so zu wählen, dass \( \sum_{n} P_{n} = 1 \) gilt: \[ Z = \sum_{n} \, e^{ - \sum_{i=1}^{I} \, \frac{\lambda_{i}}{k} \, (a_{i})_{n} } \] Die \( \lambda_{i} \) sind so zu wählen, dass die \(I\) Nebenbedingungen (vorgegebenen Mittelwerte) erfüllt sind: \[ a_{i} = \langle \hat{A}_{i} \rangle = \sum_{n} \, P_{n} \, (a_{i})_{n} \] für \(i = 1\) bis \(I\).
|
Natürlich müssten wir noch nachweisen, dass die Entropie
für dieses Ensemble tatsächlich maximal wird (und nicht minimal).
Wir wollen das hier überspringen.
Rechnen wir aber zumindest noch die Entropie aus:
\[
S =
\]
\[
= - k \, \sum_{n} \, P_{n} \, \ln{ P_{n} } =
\]
\[
= - k \, \sum_{n} \, P_{n}
\, \left( \ln{ \left( \frac{1}{Z} \right) } -
\sum_{i=1}^{I} \, \frac{\lambda_{i}}{k}
\, (a_{i})_{n} \right)
=
\]
\[
= k \, \ln{ Z }
+
\sum_{i=1}^{I} \, \lambda_{i}
\, \sum_{n} \, P_{n}
\, (a_{i})_{n}
=
\]
\[
= k \ln{ Z }
+ \sum_{i=1}^{I} \, \lambda_{i} \,
\langle \hat{A}_{i} \rangle
\]
Vergleichen wir dies mit der zu maximierenden Funktion
\[
S - \sum_{i} \, \lambda_{i} \,
\langle \hat{A}_{i} \rangle
\]
von oben, so sehen wir, dass diese zu maximierende Funktion gleich
\[
k \ln{ Z }
\]
ist (zumindest wenn wir die nullte Bedingung schon einbauen,
also \(Z\) bereits die obige Form hat).
Außerdem sehen wir, dass sich die \( \lambda_{i} \) als partielle Ableitungen der Entropie nach den vorgegebenen Mittelwerten schreiben lassen (eigentlich müsste man hier etwas sorgfältiger sein, aber sei's drum ...): \[ \frac{\partial S}{\partial \langle\hat{A}_{i} \rangle} = \lambda_{i} \] Man kann das Thema noch sehr viel weiter in der allgemeinen Form verfolgen, was hier aber zu weit führen würde (mehr dazu siehe M.Stingl: Statistische Mechanik, Kapitel 3 ). Interessant wäre auch beispielsweise, wie sich das Volumen in diese Beschreibung einfügt – ist doch das Volumen ein äußerer Parameter im Hamiltonoperator (genauer: eine Randbedingung an die Wellenfunktionen) und keine quantenmechanische Observable. Aber auch das würde hier zu weit führen. Schauen wir uns nur noch die drei Spezialfälle an, die zum mikrokanonischen, kanonischen und großkanonischen Ensemble führen:
mikrokanonisches Ensemble:
Hier gibt es neben der Wahrscheinlichkeitsnormierung keinen weiteren vorgegebenen Mittelwert, d.h. \[ I = 0 \] \[ \lambda_{i} = 0 \] Man gibt den Hilbertraum der erreichbaren Mikrozustände komplett vor, indem man \(E\) (mit Intervall \(\delta E\)), \(V\) und \(N\) festlegt. Dieser Hilbertraum umfasst dann nur endlich viele Zustände. Setzen wir \( \lambda_{i} = 0 \) in den Formeln oben ein, so erhalten wir die bekannten Formeln
| \[ P_{n} = \frac{1}{Z} \, e^{ - \sum_{i=1}^{I} \, \frac{\lambda_{i}}{k} \, (a_{i})_{n} } = \] \[ = \frac{1}{Z} =: \frac{1}{\Omega} \] |
Dabei ist
\[
Z = \sum_{n} \, e^{
-
\sum_{i=1}^{I} \, \frac{\lambda_{i}}{k}
\, (a_{i})_{n} } =
\]
\[
= \sum_{n} \, 1 =: \Omega
\]
die Anzahl der erreichbaren Mikrozustände.
kanonisches Ensemble:
Nun wird \(E\) nicht mehr mit kleinem Intervall vorgegeben, sondern der Mittelwert von \(E\) wird durch Kontakt mit einem Wärmebad fixiert. Hier ist also \[ I = 1 \] \[ \hat{A}_{1} = \hat{H} \] \[ (a_{1})_{n} = E_{n} \] mit dem Hamiltonoperator \(\hat{H}\). Wir setzen außerdem \[ \lambda_{1} =: \frac{1}{T} \] Das ergibt
| \[ P_{n} = \frac{1}{Z} \, e^{ - \sum_{i=1}^{I} \, \frac{\lambda_{i}}{k} \, (a_{i})_{n} } = \] \[ = \frac{1}{Z} \, e^{ - \frac{E_{n}}{kT} } \] |
Der Lagrange-Parameter \(1/T\) bestimmt dabei den Energie-Mittelwert.
Natürlich ist \(T\) unsere Temperatur, wie ein Vergleich mit den Formeln
aus Kapitel 1a und Kapitel 1b zeigt.
großkanonisches Ensemble:
Zusätzlich zu \(E\) wird nun auch die Teilchenanzahl \(N\) nicht mehr fest vorgegeben, sondern nur noch ihr Mittelwert durch ein Wärme-Teilchen-Reservoir fixiert. Hier ist also \[ I = 2 \] und zusätzlich zum kanonischen Ensemble noch \[ (a_{2})_{n} = N_{n} \] Wir setzen \[ \lambda_{2} =: - \frac{\mu}{T} \] sowie \[ Z =: Z_{G} \] und erhalten
| \[ P_{n} = \frac{1}{Z} \, e^{ - \sum_{i=1}^{I} \, \frac{\lambda_{i}}{k} \, (a_{i})_{n} } = \] \[ = \frac{1}{Z_{G}} \, e^{ - \frac{E_{n}}{kT} + \frac{\mu N_{n}}{kT} } \] |
Hier bezeichnet man \(Z_{G}\) auch als großkanonische Zustandssumme.
Der zweite Lagrange-Parameter \(\mu\) (das chemische Potential)
legt dabei den Mittelwert der Teilchenzahl fest.
Das soll an Beispielen genügen. Es ist interessant, die obige Herleitung dieser Ensembles mit der
entsprechenden klassischen Herleitung aus Kapitel 1b zu vergleichen:
Dort hatten wir unser System und das Wärmebad noch zu einem großen Gesamtsystem zusammenfassen müssen, das dann durch ein mikrokanonische Ensemble beschrieben wurde. Das hatte den Vorteil, dass wir mit einer sehr anschaulichen Definition für die Entropie des Gesamtsystems starten konnten, nämlich mit \[ S = k \, \ln{ \Omega } \] Man versteht anschaulich hier schnell, dass \(S\) im Gleichgewicht der beiden Teilsysteme maximal wird, denn der Makrozustand mit den meisten Mikrozuständen wird im Mittel gewinnen. Allerdings benötigt man die Idee eines makroskopisch abgeschlossenen Systems, denn nur so lässt sich diese anschauliche Entropiedefinition verwenden. Die Idee von Fluktuationen muss man dann ein wenig künstlich über ein Energieintervall \( \delta E \) einbauen, damit man auch genügend Mikrozustände erwischt.
Die Vorgehensweise im aktuellen Kapitel benötigt dagegen die Idee eines makroskopisch abgeschlossenen Systems nicht, sondern kann direkt Systeme beschreiben, bei denen realistische Fluktuationen erlaubt sind. Der Preis dafür besteht darin, dass die anschauliche Entropiedefinition \[ S = k \, \ln{ \Omega } \] nicht mehr ausreicht, sondern verallgemeinert werden muss.
Dazu sind einige Zusatzüberlegungen nötig, die man bei der klassischen Vorgehensweise nicht braucht. So muss man die Entropie \(S\) als ein Maß für das Informationsdefizit des Makrozustandes begreifen und dann nach dem Grundsatz minimaler Voreingenommenheit ein Maximum dieses Defizits im Gleichgewicht postulieren. Außerdem muss man sich über die physikalische Natur der Lagrange-Parameter erst noch klar werden. Es ist zwar unmittelbar klar, dass die Lagrange-Parameter die Mittelwerte der fluktuierenden Größen festlegen, aber wie das durch Kontakt mit einem Wärmebad geschieht, muss man sich noch überlegen.
Beide Vorgehensweisen haben also ihre Vor- und Nachteile. Für den Anfang eignet sich vermutlich die anschaulichere Vorgehensweise aus Kapitel 1a und Kapitel 1b besser.
Wenn man dann später die Hintergründe genauer verstehen will, dann rundet die abstraktere und allgemeinere Vorgehensweise im aktuellen Kapitel das Bild erst richtig ab. Aus streng theoretischer Sicht ist sie vermutlich sogar zu bevorzugen, und Stingl geht ja auch konsequent so vor. Es besteht aber die Gefahr, dass man jemanden, der sich erst einarbeiten will, überfordert, wenn man ihm nur die abstraktere Vorgehensweise zeigt.
Mit diesem Kapitel und Kapitel 1a sowie Kapitel 1b haben wir uns ein recht umfassendes Bild von der Entropie machen können. Im einfachsten Fall war Entropie dabei proportional zur Stellenzahl der Anzahl Mikrozustände, die ein Makrozustand umfasst. Statt Mikro- und Makrozustand könnte man auch Mikro- und Makro-Beschreibung sagen. Ein Mikrozustand umfasst dabei sehr detaillierte Informationen über das System, ein Makrozustand dagegen zumeist nur wenige grobe Informationen. Diese Idee konnten wir im aktuellen Kapitel konkretisieren und Entropie allgemein als ein additives Maß für unsere Unwissenheit über den Mikrozustand des Systems verstehen, wenn wir nur den Makrozustand haben.
Eigentlich hatte ich gedacht, dass es uns mit unserem detaillierten Wissen über Entropie und Information nun möglich sein sollte, Maxwells Dämon und ähnliche Dämonen zu verstehen.
Ein solcher Dämon ist in der Lage, den Mikrozustand eines Systems zu messen und dieses System dann so zu manipulieren, dass seine Entropie sinkt bzw. dass man aus Wärme Arbeit gewinnen kann (Perpetuum Mobile).
So kann der Dämon beispielsweise an einem kleinen Loch in der Trennwand zweier Gasbehälter sitzen und dieses Loch gezielt öffnen und schließen, so dass er nur schnelle Gasteilchen nach rechts und nur langsame Gasteilchen nach links durchlässt. Dadurch erzeugt er ein Temperaturgefälle zwischen den beiden Gasbehältern und eine entsprechende Entropieabnahme im Gesamtsystem der beiden Behälter, im Widerspruch zum zweiten Hauptsatz der Thermodynamik.
Wie kann das sein? Wie kann der Dämon den zweiten Hauptsatz der Thermodynamik aushebeln?
Leider musste ich feststellen, dass eine wirklich befriedigende Antwort auf dieses Problem nicht einfach zu haben ist. Seitdem James Clerk Maxwell im Jahr 1871 das Problem aufgeworfen hatte, dachte man immer wieder, man hätte eine solche Antwort gefunden, und immer wieder stellten sich Lücken in der Argumentation heraus.
Zunächst einmal ist klar, dass man den Dämon als Teil des Systems beschreiben muss. Falls man es mit einem einfachen mechanischen Dämon zu tun hat (beispielsweise mit Feynmans Ratsche), so besteht die Lösung oft darin, dass die Mikro-Mechanik auch statistische Wärmebewegungen ausführt und deshalb ihren Zweck gar nicht erfüllt, die Entropie also nicht verringert.
Schwieriger ist es bei intelligenten Dämonen, die Mikro-Messungen durchführen und dann entsprechend reagieren.
Hier dachte man erst, dass es die Messung sei, die eine Entropieerhöhung bewirkt und damit den zweiten Hauptsatz rettet (Leó Szilárd 1929).
Es zeigte sich jedoch, dass man im Prinzip auch Messungen machen kann, die die Entropie nicht erhöhen, da sie Information nur kopieren (Charles Bennet 1982).
Die Lösung scheint wohl darin zu liegen, dass man den Dämon als Computer verstehen muss, der Informationen verarbeitet und speichert. Führt er dabei irreversible Rechenschritte durch (insbesondere das Zurücksetzen des Speichers), so hat dies Einfluss auf die Entropie des Gesamtsystems, zu dem er mit dazu gehört (Rolf Landauer 1961, Charles Bennett 1982). Dabei muss man allerdings über physikalische Implementierungen des Dämon-Computers nachdenken und so logische mit physikalischer Irreversibilität verbinden. Eine detaillierte Analyse dazu findet man beispielsweise in Short et al.: The Connection between Logical and Thermodynamical Irreversibility, July 2005.
Man kann das Thema auch mit Hilfe von Methoden der algorithmischen Informationstheorie angehen (siehe Die Grenzen der Berechenbarkeit, Kapitel 3.3). Genaueres dazu findet man beispielsweise in Tobias Marriage, Prof. Groth: Computing Entropy: Understanding Maxwell's Demon, 1998 (habe ich im Internet nicht mehr gefunden). Auf Seite 12 findet man dort den interessanten Satz:
Geht man also in die Details, so taucht sogar Gödels Unvollständigkeitssatz auf (incompleteness of the demon's formal system) und verhindert, dass der Dämon allmächtig ist und mit jedem statistischen Ensemble optimal-effizient klarkommt.
Insgesamt entsteht der Eindruck, dass man zwar bereits große Fortschritte erzielt hat, um Maxwells Dämon zu verstehen, dass das Thema aber auch heute noch intensiv diskutiert wird und selbst mehr als 150 Jahre Jahre nach seiner Formulierung durch Maxwell noch immer Gegenstand der Forschung ist. Es würde jedoch zu weit führen, das hier genauer auszuführen.
Im nächsten Kapitel wollen wir uns mit einem sehr interessanten Thema befassen, das im Niemandsland zwischen Quantenmechanik, allgemeiner Relativitästtheorie (Gravitation) und statistischer Physik liegt: die Entropie schwarzer Löcher. Das ist schon deshalb interessant, weil man für die Entropie schwarzer Löcher eigentlich eine Quantentheorie der Gravitation benötigt, um die Mikrozustände des schwarzen Loches angeben zu können. Eine solche Theorie gibt es bis heute aber nicht! Trotzdem lässt sich die Entropie schwarzer Löcher berechnen – ein Meilenstein auf der Suche nach einer Quantentheorie der Gravitation!
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 30 November 2023