Das Halteproblem und die Unvollständigkeit mathematischer Axiome
Algorithmen und Mathematik
Was bedeutet das Representation Theorem?
Gödels erster Unvollständigkeitssatz
Ein weiterer Beweis für die Unvollständigkeit
Und noch ein Beweis für die Unvollständigkeit
Es gibt auch vollständige Axiomensysteme
Wir habe im letzten Unterkapitel gelernt, was wir unter einer berechenbaren Funktion \( f(n) \) verstehen wollen: eine Zuordnung, die natürliche Zahlen auf natürliche Zahlen abbildet, mit zugehöriger Rechenvorschrift. Dabei haben wir mit Hilfe der Turingmaschine eine präzise Definition des Begriffs Rechenvorschrift oder Algorithmus erhalten. Diese Definition hat es uns ermöglicht, einige interessante und teilweise überaschenden Ergebnisse zu gewinnen:
Das zentrale Instrument der Beweisführung war dabei das Cantorsche Diagonalverfahren, mit dem sich Funktionen konstruieren ließen, die in einer vorgegebenen unendlichen Liste nicht enthalten sind.
Doch was bedeutet dies alles für den Versuch, eine solide Grundlage für die gesamte Mathematik aufzubauen und alle mathematischen Wahrheiten auf eine Liste von Grundwahrheiten (Axiome) zurückzuführen?
Man kann diese Frage mit sehr verschiedener Detailtiefe angehen. In der einfachsten Stufe könnte man beispielsweise die folgende Antwort geben (siehe z.B. G. J .Chaitin: Randomness in Arithmetic and the Decline and Fall of Reductionism in Pure Mathematics):
Turings Halteproblem ist unlösbar, d.h. es gibt keinen allgemeinen Algorithmus, mit dem man für jedes beliebig vorgegebene Turingprogramm und für jeden beliebig vorgegebenen Eingabewert \( n \) entscheiden kann, ob das Turingprogramm für dieses \( n \) anhält oder nicht. Dabei interpretieren wir jedes beliebige Turingprogramm als ein Programm zur Berechnung eines Funktionswertes \( f(n) \) bei auf dem Band vorgegebenem Eingabewert \(n\). Wir erinnern uns: wenn das Turingprogramm nicht in der sogenannten Standardkonfiguration anhält, haben wir einfach \( f(n) \) als nicht definiert angesehen. Daher war es nicht notwendig, bestimmte Turingprogramme aus der Liste aller Turingprogramme auszusortieren. Man kann die obige Aussage also leicht folgendermaßen verallgemeinern:
Nun kann man die Frage, ob ein vorgegebener Algorithmus (realisiert als Turingprogramm) anhält oder nicht, als ein mathematisches Problem ansehen, denn ein Algorithmus ist vollständig durch ein festes Regelwerk festgelegt und sollte deshalb einer mathematischen Analyse zugänglich sein. Tatsächlich ist es möglich, Turings Halteproblem in die formale Sprache der Peano-Axiome (also in die sogenannte Peano-Arithmetik) zu übersetzen. Hilberts Vision war ein vollständiges, widerspruchsfreies formales mathematisches System, aus dessen Axiomen sich alle mathematischen Wahrheiten ableiten lassen. Wenn diese Vision umsetzbar ist, muss sich Turings Halteproblem durch eine mathematische Analyse des jeweiligen Programms zumindest im Prinzip immer klären lassen, denn entweder ist die Aussage das Turingprogramm hält an wahr, oder ihr Gegenteil ist wahr. Doch genau das geht nicht, wie wir im letzten Unterkapitel gesehen haben: die Frage lässt sich zwar im Einzelfall mitunter klären, jedoch nicht generell für beliebige Programme. Es gibt kein allgemeines Entscheidungsverfahren, das alle mathematischen Probleme löst. Und das bedeutet, dass es ein alle mathematische Wahrheiten umfassendes formales System nicht geben kann. Hilberts Vision erweist sich als nicht umsetzbar! Es gibt kein vollständiges und zugleich widerspruchsfreies formales System für alle mathematischen Fragestellungen.
Es ist erstaunlich, mit welchen einfachen Mitteln sich dieses tiefgreifende Ergebnis beweisen lässt. Alles, was wir benötigen, ist Cantors Diagonalverfahren, angewendet auf die Liste aller berechenbarer Funktionen. Es war Turings Idee, Gödels Ergebnis auf diese fundamentale und zugleich tiefgreifende Weise abzuleiten.
Nun ist die obige Argumentation natürlich recht allgemein. Das dort angesprochene alle mathematische Wahrheiten umfassende formale System wird nicht explizit dargestellt, und es bleibt unklar, wie ein solches System überhaupt aussehen soll. Und wie soll die mathematische Analyse von Turings Halteproblem in einem solchen System überhaupt aussehen?
Versuchen wir daher, ein konkretes formales System zu untersuchen: das formale System für die Arithmetik natürlicher Zahlen inclusive deren Addition und Multiplikation, so wie wir es in Kapitel 2.1 kennengelernt haben. Die Axiome dieses Systems sind die Peano-Axiome und die vier Axiome für die Addition und Multiplikation. Hinzu kommen die Axiome der Logik, die wir nicht explizit dargestellt haben. Wir wollen dieses formale System im Folgenden als Peano-Arithmetik bezeichnen (auch der Begriff Arithmetik erster Ordnung (first order arithmetic) ist gebräuchlich).
Es gibt nun einen ganz zentralen Zusammenhang zwischen diesem formalen System und den berechenbaren Funktionen im Sinne Turings:
Was genau bedeutet dieser Satz? Betrachten wir eine berechenbare Funktion \( f \) , die natürliche Zahlen auf natürliche Zahlen abbildet. Dann sagen wir: diese Funktion \( f \) ist darstellbar im formalen System der Peano Arithmetik, wenn es in diesem formalen System eine wohlgeformte Aussage \( A(n,p) \) mit zwei freien Variablen gibt, die folgende Eigenschaften besitzt:
\( \forall n : \, \forall p : \, \forall q : \, \left( \, A(n,p) \land A(n,q) \, \right) \implies \left( \, p = q \, \right) \)
Die erste Eigenschaft besagt (zusammen mit der zweiten Eigenschaft), dass wenn \( f(n) = p \) ist und gleichzeitig \( f(n) = q \), dann müssen \( p \) und \( q \) gleich sein. Jedem Eingabewert \( n \) wird also durch die Aussage \( A(n,p) \) ein eindeutiger Ausgabewert \( p \) zugeordnet, d.h. es liegt ein funktionaler Zusammenhang vor.
Die zweite und die dritte Eigenschaft besagen, dass ein berechenbarer funktionaler Zusammenhang \( f(n) = p \) durch eine beweisbare Aussage ausgedrückt werden kann. Besteht dieser Zusammenhang nicht, so wird dies durch die gegenteilige Aussage ausgedrückt, die dann beweisbar ist.
Das Representation Theorem ist nicht auf Funktionen einer natürlichen Variable beschränkt. Es lässt sich leicht auf Funktionen mit mehreren Variablen verallgemeinern.
Der Beweis des Representation Theorems ist nicht ganz einfach. Geht man von der Definition der Berechenbarkeit über Turingprogramme aus, so besteht der Beweis darin, einen Algorithmus anzugeben, der Turingprogramme zur Berechnung von Funktionen in Ausdrücke der Peano-Arithmetik umwandelt, die diese Funktionen darstellen. Man konstruiert also einen wohlgeformten Ausdruck der Peano-Arithmetik, der die Rechenvorschrift enthält. Wie das geht, findet man beispielsweise in Karlis Podnieks Hyper-textbook What is Mathematics: Gödel's Theorem and Around . Dort ist auch in Kapitel 3.3 das Representation Theorem beschrieben.
Letztlich bedeutet es, dass sich jede Rechenvorschrift für natürliche Zahlen im formalen System der Peano Arithmetik ausdrücken lässt. Alles, was sich durch Berechnung in den natürlichen Zahlen erreichen lässt, lässt sich in der Peano Arithmetik ausdrücken und beweisen. Statt darstellbar müsste man deshalb vielleicht besser durch einen Beweis einfangbar (capturable in proof) sagen. Aufgrund des Representation Theorems sagt man, dass die Peano Arithmetik ein hinreichend starkes formales System ist.
Betrachten wir als Beispiel die Beschreibung von Eigenschaften natürlicher Zahlen. Beispielsweise sind einige Zahlen Primzahlen, andere nicht. Eine Eigenschaft natürlicher Zahlen wird dadurch definiert, dass man zu jeder natürlichen Zahl angibt, ob sie die Eigenschaft besitzt oder nicht. Die Eigenschaft wird also z.B. durch eine überall definierte Funktion \( f \) beschrieben, wobei man folgendes festlegen kann:
Offenbar gibt es bei dieser Definition mehrere Funktionen, die dieselbe Eigenschaft definieren. Man kann jede dieser Funktion \(f\) leicht so modifizieren, dass \( f(n) = 0 \) ist, wenn \( n \) die Eigenschaft nicht besitzt. Dann würde die Eigenschaft durch eine eindeutige, überall definierte Funktion beschrieben. Dieses Detail ist allerdings nicht weiter wichtig.
Beschränken wir uns auf die berechenbaren Eigenschaften, d.h. die zugehörige (überall definierte) Funktion \(f\) ist berechenbar. Das Representation Theorem sagt dann, dass sich jede berechenbare Eigenschaft durch eine Aussage \( A(n,1) \) der Peano-Arithmetik darstellen lässt. Wenn die natürliche Zahl \( n \) die Eigenschaft besitzt (d.h. \( f(n) = 1 \)), so kann man \(A(n,1)\) aus den Axiomen ableiten. Andernfalls lässt sich \( \neg A(n,1) \) ableiten. Da die Aussage \(A(n,1)\) nur noch eine freie Variable besitzt, wollen wir sie mit \( A(n) \) bezeichnen.
Ein Beispiel für eine berechenbare Eigenschaft ist die Primzahl-Eigenschaft. Eine Zahl \( n \) ist eine Primzahl, wenn sie nur durch Eins oder durch sich selbst teilbar ist. Ein Programm, dass eine Zahl \( n \) daraufhin überprüft, müsste einfach nur diese Zahl der Reihe nach durch alle Zahlen \( m \) von 2 bis \(n - 1 \) teilen und überprüfen, ob die Division ohne Rest aufgeht. Ein solches Programm würde für jedes \( n \) nach endlich vielen Schritten ermitteln, ob \( n \) eine Primzahl ist oder nicht. Anschließend könnte man dieses Programm in einen wohlgeformten Ausdruck der Peano-Arithmetik umwandeln. Das Ergebnis wäre ein ziemlich komplizierter Ausdruck, der den kompletten Algorithmus enthält.
Es gibt jedoch i.A. mehrere gleichwertige (d.h. ineinander umformbare) Möglichkeiten, eine Eigenschaft durch einen wohlgeformten Ausdruck zu charakterisieren, genauso wie es viele gleichwertige Algorithmen zur Überprüfung der Primzahleigenschaft gibt. Eine einfache Möglichkeit ist die folgende: \begin{equation} \neg \left\{ \, \exists m: \, \exists n: \, [ p = m \cdot n ] \, \land \, [ \, \neg (m = 0^*) \land \neg ( m = p) \, ] \, \right\} \end{equation} Diese Aussage können wir als wohlgeformte Zeichenkette \(A(p)\) abkürzen. In lesbares Deutsch übersetzt bedeutet sie: Eine Primzahl \( p \) kann nicht als Produkt zweier natürlicher Zahlen \( m \) und \( n \) geschrieben werden (also nicht als \( p = m \cdot n \) ), wobei \( m \) ungleich 1 (geschrieben als \( 0^*\), also als Nachfolger von Null) und ungleich \( p \) ist.
Die entscheidende Frage lautet nun: Ist die Peano-Arithmetik ein widerspruchsfreies und vollständiges formales System? Erinnern wir uns: Widerspruchsfrei bedeutet, dass man nicht gleichzeitig eine Aussage \(A\) und die dazu verneinte Aussage \(\neg A\) beweisen (in endlich vielen Schritten ableiten) kann. Vollständig bedeutet, dass für jede wohlgeformte Aussage \(A\) entweder diese Aussage \(A\) oder die gegenteilige Aussage \(\neg A\) bewiesen werden kann. Wenn die Peano-Arithmetik widerspruchsfrei und vollständig ist, so ließe sich jede in dieser Sprache ausdückbare Wahrheit beweisen. Wir hätten ein universelles mathematisches System im Sinne Hilberts für die natürlichen Zahlen gefunden. Da die Peano-Arithmetik aufgrund des Representation Theorems zumindest alle berechenbaren Wahrheiten umfasst, liegt die Vermutung nahe, dass dies alle Wahrheiten sind. Doch wir werden sehen ... .
In Kapitel 2.2 haben wir gesehen, dass jedes zugleich vollständige und widerspruchsfreie formale System ein Entscheidungsverfahren besitzt. Es gibt also einen Algorithmus, der für jeden vorgegebenen wohlgeformten Ausdruck eine Entscheidung darüber erlaubt, ob dieser Ausdruck aus den Axiomen ableitbar ist oder nicht.
Wenn wir nun zeigen könnten, dass es kein Entscheidungsverfahren in der Peano-Arithmetik gibt, so hätten wir damit gleichzeitig auch bewiesen, dass sie nicht zugleich vollständig und widerspruchsfrei ist. Ein formales System könnte sogar unvollständig sein und trotzdem ein Entscheidungsverfahren besitzen. Daher wollen wir gleich versuchen, zu überprüfen, ob die Peano-Arithmetik ein Entscheidungsverfahren besitzt, denn dies ist die schärfere Aussage.
Nehmen wir also an, die Peano-Arithmetik besitzt ein Entscheidungsverfahren. Dann könnte man für jede wohlgeformte Aussage \(A\) entscheiden, ob sie beweisbar (d.h. aus den Axiomen ableitbar) ist oder nicht. Dasselbe gilt für die gegenteilige Aussage \(\neg A\).
Nun wissen wir aus Kapitel 2.2, dass wir eine (unendlich lange) Liste aller wohlgeformten Aussagen (Zeichenketten) der Peano-Arithmetik aufstellen können. Jede (richtige oder falsche) Aussage über natürliche Zahlen, die sich in der formalen Sprache der Peano-Arithmetik ausdrücken lässt, ist in dieser Liste zu finden. Dabei ist nicht gefordert, dass die Aussagen aus den Axiomen ableitbar sind. Sie müssen nur den Syntaxregeln genügen. Wenn eine wohlgeformte Aussage \(A\) in der Liste vorkommt, so kommt auch die Aussage \(\neg A\) in der Liste vor, denn sie ist ebenfalls wohlgeformt.
Man kann nun aus dieser Liste alle Aussagen entfernen, die nicht genau eine freie Variable haben, denn anhand der Syntaxregeln kann man für jede Aussage mechanisch in endlich vielen Schritten entscheiden, ob sie genau eine freie Variable besitzt oder nicht. Das Ergebnis ist eine vollständige Liste aller wohlgeformten Aussagen mit einer freien Variablen.
Wir wollen die einzelnen Aussagen in dieser Liste mit \( A_m(n) \) bezeichnen. Dabei ist \( m \) die Zeilennummer, in der die Aussage in der Liste steht. Wenn wir nun der Reihe nach alle natürlichen Zahlen für \( n \) einsetzen, können wir die folgende Tabelle aufstellen:
Nun verwenden wir unsere Annahme, dass es ein Entscheidungsverfahren gibt, d.h. für jeden Eintrag \( A_m(n) \) in dieser Tabelle können wir in endlich vielen Schritten mechanisch entscheiden, ob er aus den Axiomen ableitbar (beweisbar) ist oder nicht. Damit können wir die Liste aller Aussagen in eine (nicht unbedingt vollständige) Liste überall definierter berechenbarer Funktionen übersetzen. Zu jeder Aussage \( A_m(n) \) definieren wir eine Funktion \( f_m(n) \), indem wir festlegen:
Diese Funktion ist überall definiert, und sie ist berechenbar, denn das Entscheidungsverfahren garantiert, dass wir in endlich vielen Schritten wissen, ob \( A_m(n) \) beweisbar ist oder nicht.
Damit können wir auch die Tabelle der \( A_m(n) \) in eine Tabelle der \( f_m(n) \) übersetzen:
Diese Tabelle besteht nur aus Nullen und Einsen: wenn \( A_m(n) \) beweisbar ist, steht an dieser Stelle eine Eins, im anderen Fall eine Null. Die Tabelle könnte also beispielsweise so aussehen:
Wir hatten diese Tabelle aus der vollständigen Tabelle aller wohlgeformten Aussagen mit einer freien Variablen erhalten. Daher ist die Frage naheliegend, ob auch die obige Tabelle vollständig ist: Sind alle berechenbaren, überall definierten Funktionen mit Funktionswerten Null oder Eins darin enthalten?
In Kapitel 2.3 hatten wir bereits eine ähnliche Frage untersucht. Dabei hatten wir folgendes Ergebnis erhalten: Es gibt keine per Algorithmus erzeugbare vollständige (unendlich lange) Liste aller berechenbaren, überall definierten Funktionen einer natürlichen Variablen. Den Beweis hatten wir mit Cantors Diagonalverfahren geführt.
Der einzige Unterschied ist, dass wir nun nur Funktionen mit Wertebereich Null und Eins betrachten. Das spielt jedoch für den Beweis keine Rolle, denn wir können Cantors Diagonalverfahren auch hier anwenden, um eine neue Funktion zu konstruieren, die nicht in der obigen Liste enthalten ist. Wir definieren also eine Funktion \( f_d \), so dass \( f_d(n) = 1 \), wenn \( f_n(n) = 0 \) ist und umgekehrt. Anhand der Liste
(Diagonalelemente hier fett dargestellt) würden wir also die Funktion \( f_d \) so definieren:
Diese neue Funktion ist berechenbar, überall definiert, und sie ist nicht in der Liste enthalten, die wir aus der Aussagenliste konstruiert haben.
Nun können wir den Kreis schließen und von den Funktionen zurück zu den Aussagen gehen. Dies ermöglicht uns das Representation Theorem. Es garantiert uns, dass jede berechenbare Funktion \( f_m(n) \) durch eine Aussage \( A_m(n,p) \) dargestellt werden kann. In unserem Fall ist \( p = 1 \) und wir schreiben statt \( A_m(n,1) \) einfacher \( A_m(n) \). Es gibt also zu jeder überall definierten Funktion \( f_m(n) \) mit Wertebereich Null und Eins eine wohlgeformte Aussage \( A_m(n) \), so dass gilt:
Das Representation Theorem gilt nicht nur für die Funktionen aus unserer Liste, sondern auch für die neue Funktion \( f_d(n) \). Also muss es auch für diese Funktion eine wohlgeformte Aussage (nennen wir sie \( A_d(n) \) ) geben, die die obigen Bedingungen erfüllt. Und diese wohlgeformte Aussage muss in unserer Liste aller wohlgeformter Aussagen enthalten sein.
Wenn aber \( A_d(n) \) in der Liste enthalten ist, so muss daraus bereits zuvor die Funktion \( f'_d(n) \) in unserer Funktionenliste entstanden sein, als wir zu jeder Aussage eine Funktion konstruiert hatten (der Strich soll diese Funktion von \( f_d(n) \) unterscheiden, die wir durch Cantors Diagonalverfahren gewonnen haben).
Sind \( f'_d(n) \) und \( f_d(n) \) dieselben Funktionen? Sammeln wir, was wir über diese beiden Funktionen wissen:
Betrachten wir den Fall \( f_d(n) = 1 \). Dann ist \( A_d(n) \) beweisbar und dann ist \( f'_d(n) = 1 \).
Umgekehrt: Wenn \( f_d(n) = 0 \) ist, dann ist \( \neg A_d(n) \) beweisbar. Wenn wir annehmen, dass die Peano-Arithmetik widerspruchsfrei ist, so ist dann \( A_d(n) \) nicht beweisbar, und es folgt \( f'_d(n) = 0 \).
Die Funktionen \( f_d \) und \( f'_d \) sind damit identisch. Sie können aber nicht identisch sein, denn \( f'_d \) ist in der Liste enthalten, die wir zu der Liste aller wohlgeformter Ausdrücke erzeugt haben, \( f_d \) wurde dagegen gerade so konstruiert, dass es nicht in der Liste ist. Wir haben einen Widerspruch erhalten
Unsere Annahme, dass es ein Entscheidungsverfahren gibt, muss also falsch gewesen sein, denn diese Annahme führt zu einem Widerspruch. Halten wir unser Ergebnis fest:
Und damit folgt:
Denn wäre sie widerspruchsfrei und vollständig, so hätte sie ein Entscheidungsverfahren.
Gödel hatte seinen ersten Unvollständigkeitssatz auf andere Weise bewiesen. Er konstruierte explizit eine wohlgeformte Aussage, die nicht beweisbar sein kann, wenn die Peano-Arithmetik widerspruchsfrei ist. Wir werden uns im nächsten Unterkapitel ansehen, wie das geht. Gödels erster Unvollständigkeitssatz lässt jedoch die Frage offen, ob es ein Entscheidungsverfahren gibt. Dies konnten wir durch Verwendung des Representation Theorems und mit Cantors Diagonalverfahren eindeutig klären. Bereits Turing hatte diesen Zusammenhang 1936 in seiner berühmten Arbeit On Computable Numbers With an Application to the Entscheidungsproblem hergeleitet.
Fassen wir noch einmal die wesentlichen Schritte des Beweises zusamen:
Wir starten mit der Liste aller wohlgeformten Aussagen mit einer freien Variablen der Peano-Arithmetik
(eine solche Liste gibt es). Wenn es ein Entscheidungsverfahren
in der Peano-Arithmetik gibt, können wir zu jeder Aussage \( A_m(n) \)
in der Liste angeben, ob sie für die natürliche Zahl \( n \)
aus den Axiomen ableitbar ist oder nicht. Damit lässt sich
zu jeder Aussage aus der Liste eine überall definierte berechenbare Funktion
konstruieren, die gleich Eins ist, wenn die Aussage ableitbar ist, und die gleich Null ist,
wenn die Aussage nicht ableitbar ist. Die so konstruierte Liste von Funktionen ist
unvollständig, denn mit Cantors Diagonalverfahren lässt sich eine neue berechenbare,
überall definierte Funktion
konstruieren, die nicht in der Liste enthalten ist. Das Representation Theorem
(d.h. die beweisbare Tatsache, dass die Peano Arithmetik ein hinreichend starkes
formales System ist) garantiert nun, dass diese neue Funktion sich durch eine
wohlgeformte Aussage darstellen lässt, die beweisbar ist, wenn der Funktionswert
gleich Eins ist, und deren verneinte Form beweisbar ist, wenn der Funktionswert
gleich Null ist. Diese Aussage muss bereits in der Liste aller wohlgeformten Aussagen
enthalten sein, denn diese Liste ist vollständig. Daher hätte die neue Funktion
bereits im ersten Schritt mit Hilfe des Entscheidungsverfahrens erzeugt werden müssen
und in der so erzeugten Funktionenliste auftauchen müssen, was aber nicht sein kann,
denn sie ist so konstruiert, dass sie nicht in der Funktionsliste vorhanden sein kann.
Damit haben wir einen Widerspruch erzeugt, d.h. es kann kein Entscheidungsverfahren geben.
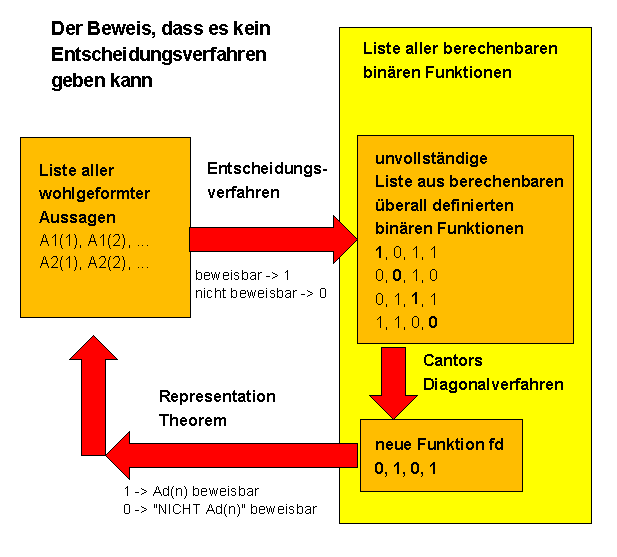
Das folgende Bild stellt diesen Zusammenhang nochmals graphisch dar:

Man kann diesen einducksvollen Beweis, der mit elementaren Mitteln ein sehr tiefgründiges Ergebnis beweist, noch etwas anders darstellen (siehe auch Peter Smith: An Introduction to Gödel's Theorems).
Statt explizit über berechenbare Funktionen mit Funktionswerten Null und Eins zu sprechen, kann man auch davon sprechen, dass eine natürliche Zahl \( n \) eine Eigenschaft \( M \) besitzt (was wir wieder durch \( f_m(n) = 1 \) kennzeichnen) oder sie nicht besitzt (d.h. \( f_m(n) = 0 \) ), denn eine berechenbare Eigenschaft von natürlichen Zahlen ist dann festgelegt, wenn man zu jeder natürlichen Zahl berechnen kann, ob sie die Eigenschaft aufweist oder nicht. Der Beweis liest sich dann so:
Wir wissen (Kapitel 2.2): Es gibt eine vollständige Liste \( A_1(n), A_2(n), ... \) aller wohlgeformten Aussagen der Peano-Arithmetik (mit einer freien Variablen \( n \) ). Wir definieren eine Eigenschaft D auf die folgende Weise:
(Dies entspricht der Definition der Funktion \( f_d \) durch Cantors Diagonalverfahren).
Nun nehmen wir an, es gibt ein Entscheidungsverfahren. Dann ist \(D\) eine berechenbare Eigenschaft, denn man kann in endlich vielen Schritten entscheiden, ob \( \neg A_n(n) \) beweisbar ist. Da die Peano Arithmetik ein hinreichend starkes formales System ist (Representation Theorem), kann sie die berechenbare Eigenschaft \(D\) darstellen. Es muss daher eine wohlgeformte Aussage (nennen wir sie \( A_d(n) \) in der obigen Liste aller wohlgeformten Aussagen geben, so dass für alle natürlichen Zahlen \( n \) gilt:
Dies gilt auch für den Spezialfall \( n = d \):
Aber die Definition der Eigenschaft \(D\) besagt für den Fall \( n = d \):
so dass wir einen Widerspruch hergeleitet haben (wenn die wohlgeformte Aussage \( \neg A_d(d) \) beweisbar ist, besitzt \(d\) die Eigenschaft \(D\), aber dann ist \( A_d(d) \) beweisbar). Wenn also die Peano-Arithmetik hinreichend stark und widerspruchsfrei ist, so kann es kein Entscheidungsverfahren geben.
Es gibt noch weitere Möglichkeiten, den Beweis zu führen. Eine ganz interessante Möglichkeit ist die folgende:
Statt in dem obigen Bild auf der linken Seite mit der vollständigen Liste aller wohlgeformten Aussagen mit einer freien Variablen der Peano-Arithmetik zu beginnen, kann man auch auf der rechten Seite mit der vollständigen Liste aller berechenbaren binären Funktionen beginnen. Das Representation Theorem garantiert nun, dass zu jeder Funktion \( f_m(n) \) aus der Liste eine wohlgeformte Aussage \( A_m(n) \) existiert, so dass gilt:
Nehmen wir nun an, es gibt ein Entscheidungsverfahren. Dann können wir wieder wie im Bild zu jeder dieser Aussagen \( A_m(n) \) eine neue überall definierte Funktion \( g_m(n) \) definieren:
Wir haben damit eine Liste überall definierter binärer berechenbarer Funktionen erzeugt. Aber ist diese Liste vollständig? Diese Frage können wir mit Hilfe einer Argumentation klären, die wir oben bereits verwendet haben:
Wenn \( f_m(n) = 1 \) ist,
dann ist \( A_m(n) \) beweisbar
und dann ist \( g_m(n) = 1 \) .
Umgekehrt:
Wenn \( f_m(n) = 0 \) ist,
dann ist \( \neg A_m(n) \) beweisbar, und
wenn wir voraussetzen, dass die Peano-Arithmetik widerspruchsfrei ist,
so ist dann \( A_m(n) \) nicht beweisbar,
und es folgt \( g_m(n) = 0 \) .
Die überall definierte Funktion \( g_m \) hat also überall da Einsen und Nullen, wo die zugehörige (überall oder partiell definierte) Funktion \( f_m \) sie hat. An den Stellen \(n\), wo \( f_m(n) \) nicht definiert ist, wird dagegen keine Aussage über den Funktionswert \( g_m(n) \) gemacht; er ist dort entweder Eins oder Null, je nachdem, ob die Aussage \( A_m(n) \) beweisbar ist oder nicht.
Wenn nun \( f_m \) überall definiert ist, so ist \( g_m \) dieselbe Funktion, denn sie hat überall dieselben Funktionswerte wie \( f_m \). Jede überall definierte Funktion aus der vollständigen Liste aller berechenbaren binären Funktionen \( f_m \) taucht also in der neuen Liste der überall definierten berechenbaren Funktionen \( g_m \) wieder auf. Damit enthält diese neue Liste alle berechenbaren überall definierten binären Funktionen, d.h. sie ist vollständig. Aber: wir wissen bereits, dass es eine solche Liste nicht geben kann, denn mit Cantors Diagonalverfahren lässt sich immer eine neue Funktion erzeugen, die nicht in der Liste enthalten ist. Damit muss unsere Annahme, dass es ein Entscheidungsverfahren gibt, falsch sein (wenn die Peano-Arithmetik widerspruchsfrei ist).
Dieser Beweis zeigt sehr schön die enge Verwandtschaft zwischen Entscheidungsverfahren und Turings Halteproblem: Nehmen wir an, Turings Halteproblem wäre lösbar. Dann können wir wie oben die vollständige Liste aller binären berechenbaren Funktionen dazu verwenden, um eine vollständige Liste aller binären berechenbaren überall definierten Funktionen aufzustellen. Wir definiernen einfach die Funktionen \( g_m \) in der neuen Liste durch
Da es diese vollständige Liste aller binären berechenbaren überall definierten Funktionen nicht geben kann, muss Turings Halteproblem unlösbar sein. Die Entscheidung, ob \( f_m(n) \) definiert ist (Turings Halteproblem), entspricht dabei der Entscheidung, ob \( A_m(n) \) beweisbar ist (Entscheidungsverfahren).
Die obigen Sätze und Beweise gelten für jedes formale System der natürlichen Zahlen, in dem das Representation Theorem gilt. Das formale System muss also stark genug sein, jede berechenbare Funktion natürlicher Zahlen darzustellen, d.h. den Rechenalgorithmus durch beweisbare wohlgeformte Zeichenketten auszudrücken. Es ist interessant, dass die Peano-Arithmetik diesen Anforderungen bereits genügt, denn sie enthält neben den Peano-Axiomen nur noch vier Axiome zur Festlegung der Addition und der Multiplikation.
Kann man dieses formale System vielleicht noch weiter ausdünnen? Es ist tatsächlich möglich, das Induktionsaxiom wegzulassen, ohne das Representation Theorem zu verlieren. Die daraus entstehende Arithmetik trägt den Namen Robinson Arithmetik. Eine kurze Begründung: Das Induktionsaxiom dient hauptsächlich dazu, Aussagen für alle natürlichen Zahlen zu beweisen. Für das Representation Theorem genügt es jedoch, viele Beweise für einzelne Zahlen zu führen.
Behalten wir nun das Induktionsaxiom und versuchen statt dessen, die beiden Axiome zur Festlegung der Multiplikation wegzulassen. Man könnte ja auf die Idee kommen, dass man dabei nichts verliert, denn schließlich kann man den Ausdruck \( 3 \cdot 4 \) als Kurzschreibweise für den Ausdruck \( 4 + 4 + 4 \) auffassen. Das entsprechende formale System mit Addition, aber ohne Multiplikation wird als Presburger Arithmetik bezeichnet.
Es zeigt sich jedoch, dass die Presburger Arithmetik nicht in der Lage ist, alle berechenbaren Funktionen darzustellen. Sie ist zu schwach dafür. Das Representation Theorem ist in ihr nicht gültig, und daher ist auch Gödels Unvollständigkeitssatz nicht zwingend.
Tatsächlich gelang es im Jahr 1929 dem Mathematiker Mojzesz Presburger, zu beweisen, dass die Presburger Arithmetik vollständig und widerspruchsfrei ist. Hilberts Vision ist also für hinreichend schwache formale Systeme durchaus umsetzbar. Jede Aussage in dieser Arithmetik lässt sich in endlich vielen Schritten entweder beweisen oder widerlegen.
Praktischen Nutzen hätte diese allgemeine Beweisbarkeit jedoch nicht. Im Jahr 1974 gelang es Michael J.Fischer und Michael O.Rabin, folgendes zu beweisen:
Der Rechenaufwand für den universellen Beweisalgorithmus steigt also mindestens doppelt exponentiell mit der Länge des zu untersuchenden Ausdrucks. Ein Beispiel: für \(C = 1 \) und \( n = 10 \) ist \( 2^{2^{C \cdot n} } = 2^{1024} \), das ist eine Eins mit etwa 300 Nullen ( \(10^{300}\) ), also weit mehr Rechenschritte als es Atome im beobachtbaren Universum gibt.
© Jörg Resag, www.joerg-resag.de
last modified on 25 February 2023