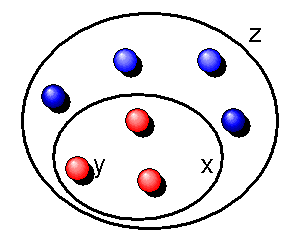
In diesem Kapitel wollen wir uns das Axiomensystem ansehen, das man als das heute bekannteste allgemein akzeptierte grundlegende Axiomensystem der Mathematik ansehen kann: die Zermelo-Fränkel-Axiome der Mengenlehre. Dieses Axiomensystem geht auf Arbeiten von Ernst Zermelo aus dem Jahr 1908 zurück und wurde später durch Adolf Fränkel, Thoralf Skolem und von Neumann bis zum Jahr 1925 weiter verfeinert. Man kann praktisch die gesamte bekannte Mathematik (bis auf gewisse Ausnahmen, die es nach dem Gödelschen Unvollständigkeitssatz immer gibt) auf diese Axiome zurückführen. Seit 1925 hat man kein neues einfaches Axiom gefunden, das dem Axiomensystem hinzugefügt werden müsste, um seine Aussagekraft entscheidend zu verbessern. Und man hat bisher auch noch keinen Widerspruch entdeckt, weshalb man annimmt, dass das System widerspruchsfrei ist (dies kann man natürlich nach Gödels zweitem Satz innerhalb des Systems nicht beweisen).
Zwei Zermelo-Fränkel-Axiome haben wir bereits im letzten Kapitel kennengelernt. Wir wollen diese Axiome und ihre Bedeutung hier noch einmal kurz wiederholen:
Dieses Axiom sagt: Wenn alle Elemente, die in der Menge \(x\) sind, auch in der Menge \(y\) sind und umgekehrt, dann sind die beiden Mengen \(x\) und \(y\) gleich. Doppelte Elemente spielen keine Rolle.
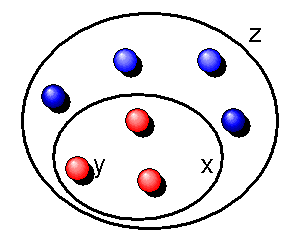
Das Axiom (oder genauer: Axiomenschema) erlaubt es, alle Elemente \(y\) einer vorgegebenen Menge z, die eine bestimmte Eigenschaft \(F(y)\) haben (in der Grafik sind sie zur Veranschaulichung beispielsweise rot), zu einer neuen Menge \(x\) zusammenzufassen (auszusondern). Die Menge \(x\) ist daher immer eine Untermenge zu der bereits bestehenden Menge \(z\).
Das Aussonderungsaxiom erlaubt es wie zuvor das Komprehensions-Axiomenschema ebenfalls, die leere Menge \( \varnothing \) zu konstruieren. Dazu setzt man für \(F(y)\) eine Aussage über \(y\) ein, die kein \(y\) erfüllen kann, z.B. die Aussage \( \neg (y=y) \): \[ \forall z : \exists x: \forall y : \, [ (y \in x) \Leftrightarrow ( (y \in z) \land \neg (y=y) ) ] \] Da \( \neg (y=y) \) für kein \(y\) gelten kann, kann man diesen Ausdruck umwandeln in \[ \forall z : \exists x: \forall y : \, [ \neg (y \in x) ] \] Wenn es auch nur eine einzige Menge \(z\) gibt, so kann man den Teil \( \forall z : \) weglassen, denn der Rest enthält keine Menge \(z\) mehr. Übrig bleibt: \[ \exists x: \forall y : \, [ \neg (y \in x) ] \] d.h. \(x\) ist die leere Menge \( \varnothing \), da sie kein einziges \(y\) enthält.
Wir wollen die Existenz wenigstens einer Menge \(z\) separat als Axiom fordern:
Alternativ kann man auch die Existenz der leeren Menge als Axiom fordern. Häufig ersetzt man dann auch das Aussonderungsaxiom komplett durch das Ersetzungsaxiom (siehe unten; dann muss man allerdings die Existenz der leeren Menge separat als Axiom fordern). Wir gehen weiter unten noch darauf ein. Wie so oft, gibt es hier verschiedene gleichwertige Formulierungen.
Im Gegensatz zu dem uneingeschränkten Komprehensions-Axiomenschema \[ \exists x: \forall y : \, [ (y \in x) \Leftrightarrow F(y) ] \] aus dem vorherigen Kapitel, das zu Widersprüchen führt, erlaubt es das Aussonderungsaxiom nicht mehr, zu jeder Eigenschaft \(F(y)\) eine neue Menge zu erzeugen. Man kann damit nur noch Untermengen zu bereits bestehenden Mengen bilden. Daher benötigt man nun weitere Axiome, die die Bildung neuer Mengen erlauben. Ein Teil dieser Axiome sind bestimmte Einschränkungen des uneingeschränkten Komprehensions-Axioms mit speziellen Eigenschaften \(F(y)\), die die Elemente der neuen Menge erfüllen müssen. Diese Axiome wollen wir uns nun der Reihe nach ansehen.
Eine erste Möglichkeit, aus gegebenen Mengen neue Mengen zu konstruieren, besteht darin, die gegebenen Mengen als Elemente einer neuen Menge zu verwenden. Dies erlaubt das folgende Axiom:
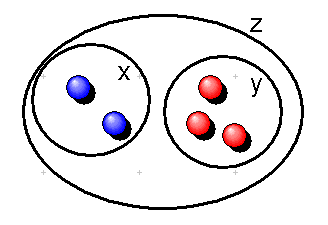
Man schreibt die entsprechende Menge \(z\) auch als \( z = \{ x, y \} \). Diese Menge wird auch oft als ungeordnetes Paar bezeichnet, da \(x\) und \(y\) keine besondere Reihenfolge in der Menge haben. Man weiß nur: \(x\) ist in \(z\), und \(y\) ist in \(z\). Ein geordnetes Paar \( (x, y) \), bei dem \(x\) vor \(y\) kommt, kann man als Menge \( \{ \{ x \}, \{ x, y \} \} \) konstruieren. Wir gehen weiter unten genauer darauf ein.
Interessant ist der Fall \(x = y\). Das Paarbildungsaxiom bewirkt dann, dass es zu jeder Menge \(x\) eine Menge \( \{ x, x \} \) gibt. Da doppelte Elemente nach dem Extensionalitäts-Axiom keine Rolle spielen, wollen wir diese Menge als \( \{ x \} \) schreiben.
Ein Beispiel: Wir setzen in einem ersten Schritt für \(x\) und \(y\) die leere Menge \( \varnothing \) ein, deren Existenz wir ja oben bewiesen haben. Die mit dem Paarbildungsaxiom neu konstruierte Menge \(z\) enthält dann die leere Menge als Element, d.h. \( z = \{ \varnothing \} \). Nun können wir erneut das Paarbildungsaxiom anwenden, wobei wir \(x = \varnothing \) und die neue Menge als \( y = \{ \varnothing \} \) verwenden, und damit die Menge \( z = \{ \varnothing, \{ \varnothing \} \} \) konstruieren. Im nächsten Schritt können wir dann z.B. die Mengen \( \{ \varnothing \} \) und \( \{ \varnothing, \{ \varnothing \} \} \) zur Menge \( \{ \{ \varnothing \} , \{ \varnothing, \{ \varnothing \} \} \} \) zusammenfassen und so fort. Allerdings entstehen auf diese Weise immer nur Mengen mit zwei Elementen. Um die Konstruktion größerer Mengen zu ermöglichen, benötigen wir ein weiteres Axiom: das Vereinigungsaxiom.
Das Vereinigungsaxiom erlaubt es, die Elemente mehrerer Mengen zu einer neuen Menge zusammenzufassen:
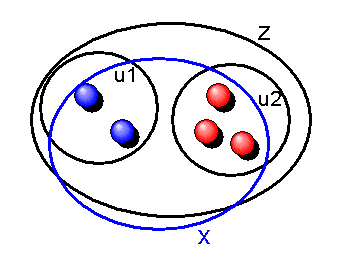
Für alle vorgegebenen Mengen (Mengensysteme) \(z\) kann man also die Elemente \(y\) der darin enthaltenen Mengen u zu einer neuen Menge \(x\) zusammenfassen. Anders ausgedrückt: Zu jedem Mengensystem \(z\) gibt es eine Menge \(x\), die alle die Elemente \(y\) enthält, die in mindestens einer Menge \(u\) des gegebenen Systems \(z\) enthalten sind. Die Menge \(x\) entsteht also dadurch, dass man in dem vorgegebenen Mengensystem \(z\) die Zwischenebene der Mengen \(u\) weglässt und deren Elemente \(y\) gleich als Elemente einer Menge \(x\) auffasst. Man sagt auch, \(x\) ist die Vereinigungsmenge aller in \(z\) enthaltenen Mengen (oder kurz: die Vereinigungsmenge des Mengensystems \(z\) ).
Das Vereinigungsaxiom ist letztlich eine spezielle Version des uneingeschränkten Komprehensions-Axiomenschemas aus dem letzten Kapitel, das zum Russelschen Widerspruch geführt hatte. Erinnern wir uns: Das (uneingeschränkte) Komprehensions-Axiomenschema lautet: \[ \exists x: \forall y : \, [ (y \in x) \Leftrightarrow F(y) ] \] Hier setzen wir für die Eigenschafts-Aussage \(F(y)\) die spezielle Aussage \( \exists u: (y \in u) \land (u \in z) \) ein (d.h. \(y\) ist Element einer Menge \(u\), die selbst Element von \(z\) ist; \(F(y)\) darf ja weitere Variablen neben \(y\) enthalten, nur nicht die Variable \(x\) ), so ergibt sich \[ \exists x : \forall y : \, [ (y \in x) \Leftrightarrow [ \exists u: (y \in u) \land (u \in z)] ] \] Da \(F(y)\) noch die freie Variable \(z\) enthält, stellen wir noch ein \( \forall z : \) voran, um die Variable zu binden, und erhalten so das Vereinigungsaxiom.
Mit dem Vereinigungsaxiom sind wir (zusammen mit dem Paarbildungsaxiom) nun in der Lage, beliebig große endliche Mengen zu konstruieren. Beispielsweise können wir mit dem Paarbildungsaxiom die Zwei-Elemente-Menge \( \{ \, \{\varnothing,\{\varnothing\}\} , \, \{\varnothing,\{\varnothing,\{\varnothing\}\}\} \, \} \) konstruieren. Diese Menge verwenden wir nun als Mengensystem \(z\) im Vereinigungsaxiom und können so die Menge \( x = \{ \varnothing, \{\varnothing\}, \{\varnothing,\{\varnothing\}\} \} \) konstruieren, die sämtliche Elemente der beiden in \(z\) enthaltenen Mengen enthält. Diese neue Menge \(x\) enthält bereits drei Elemente.
Die bisherigen Axiome ermöglichen nur die Konstruktion endlicher Mengen. Da wir auch unendliche Mengen erlauben wollen, benötigen wir ein entsprechendes Axiom:
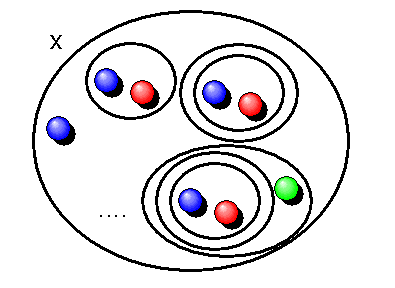
Was bedeutet dieses etwas unübersichtliche Axiom? Es fordert die Existenz einer Menge \(x\), die folgende Eigenschaften hat:
Wenn also z.B. die leere Menge \( \varnothing \) Element von \(x\) ist, dann enthält \(x\) auch eine Menge der Form \( \{ \varnothing, ... \} \) , wobei \( ... \) für irgendwelche weiteren (oder auch gar keine) Elemente steht. Dieses neue Element \( \{ \varnothing, ... \} \) führt dann ebenfalls dazu, dass \(x\) auch eine Menge der Form \( \{ \{ \varnothing, ... \}, ... \} \) enthalten muss und so fort. Auf diese Weise kann man die Menge \(x\) mit unendlich vielen Elementen bevölkern. Wir haben im letzten Kapitel gesehen, dass man diese Idee für die Konstruktion der Menge der natürlichen Zahlen in der Sprache der Mengenlehre braucht.
Das Unendlichkeitsaxiom kann man so interpretieren, dass es die Existenz aktual unendlicher Objekte fordert. Es sagt, dass eine unendlich große Menge existiert, und es sagt auch, warum die Menge unendlich groß ist. Der Begriff der aktualen Unendlichkeit steht im Gegensatz zum Begriff der potentiellen Unendlichkeit, bei dem man nur sagen würde, dass man beliebig große Mengen konstruieren kann.
Ein Beispiel für potentielle Unendlichkeit liefert die Peano-Arithmetik, wie sie durch die Peano-Axiome definiert wird (siehe Kapitel 2.1). Die natürlichen Zahlen werden dabei als Objekte dargestellt, die über die Nachfolger-Beziehung Schritt für Schritt auseinander hervorgehen. Man kann also beliebig weit zählen, aber es gibt keine Möglichkeit, ein Objekt zu definieren, das alle natürlichen Zahlen umfasst (also aktual unendlich ist). Das einzige, was man in der Peano-Arithmetik tun kann, wenn man über alle natürlichen Zahlen gleichzeitig sprechen will, besteht darin, Ausdrücke der Form \( \forall x : \, ... \) zu verwenden. Dabei können sich über die Hintertür aber Objekte hineinschleichen, die wir gar nicht unbedingt haben wollten: die übernatürlichen Zahlen (siehe Kapitel 3.1), die sich nicht als mehrfache Nachfolger der Null schreiben lassen. Wir gehen am Ende dieses Kapitels noch einmal darauf ein.
Das folgende Axiom stammt von Fränkel aus dem Jahr 1922. Es wurde hinzugefügt, um Abbildungen im System der Mengenlehre beschreiben zu können:
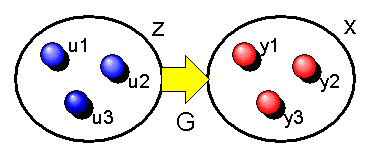
Dabei ist \(G(u)\) eine sogenannte Abbildung mit einer freien Variablen \(u\). Streng genommen ist \( y = G(u) \) eine Kurzschreibweise für eine wohlgeformte Aussage \( A(u,y) \) mit zwei Variablen, für die die Aussage \[ \forall u : \forall y : \forall z : \, [A(u,y) \land A(u,z)] \Rightarrow [y = z] \] gilt (diese Formulierung kennen wir bereits vom Representation Theorem in Kapitel 2.4). Es dürfen auch noch weitere freie Variablen in \( G(u) \) auftreten (nur \(y\) nicht). Das Ersetzungsaxiom ist wieder ein Axiomenschema, denn zu jeder Abbildung \(G(u)\) gibt es ein entsprechendes Axiom.
Was bedeutet nun dieses kompliziert aussehende Axiom?
Das Axiom sagt, dass es eine Zielmenge \(x\) gibt, die genau die Abbilder aller Elemente einer beliebig vorgegebenen Menge \(z\) enthält. Jedes Element \(y\) von \(x\) besitzt ein Urbild \(u\) aus \(z\), so dass \( y = G(u) \) ist. Und umgekehrt gibt es zu jedem Element \(u\) aus \(z\) ein Abbild \( y = G(u) \) in x. Also sagt das Axiom: Das Abbild einer beliebigen Menge unter einer Abbildung \(G\) ist wieder eine Menge.
Man kann es auch noch etwas anders ausdrücken. Dazu stellt man sich vor, dass die Abbildung \(G\) die einzelnen Elemente \(u\) der Menge \(z\) durch neue Elemente \(G(u)\) ersetzt (daher der Name Ersetzungsaxiom). Das Axiom sagt nun, dass dadurch eine neue Menge \(x\) entsteht.
Das Ersetzungsaxiom entsteht wie das Vereinigungsaxiom aus dem uneingeschränkten Komprehensions-Axiom, indem wir eine spezielle Bedingung \(F(y)\) wählen, die die Elemente der neuen Menge \(x\) erfüllen müssen. Hier noch einmal das uneingeschränkte Komprehensions-Axiomenschema: \[ \exists x: \forall y : \, [ (y \in x) \Leftrightarrow F(y) ] \] Für \( F(y) \) wählen wir die spezielle Aussage \( \exists u: \, (u \in z) \land (y = G(u)) \) (d.h. \(y\) ist das Abbild \(G(u)\) eines Elementes \(u\) aus \(z\)) und stellen \( \forall z : \) voran.
Das Ersetzungsaxiom hat Ähnlichkeit mit dem Aussonderungsaxiom, das wir oben bereits kennengelernt haben. Zur Erinnerung: das Aussonderungsaxiom lautet \[ \forall z : \exists x: \forall y : \, [ (y \in x) \Leftrightarrow ( (y \in z) \land F(y) ) ] \] und zum Vergleich noch einmal das Ersetzungsaxiom: \begin{align} \forall z : \, \exists x: \forall y : \, [ \, (y \in x) \Leftrightarrow \\ (\exists u: (u \in z) \land (y = G(u)) \, ) \, ] \end{align} Der einzige Unterschied liegt darin, dass das Ausssonderungsaxiom hinter \( \Leftrightarrow \) statt \( (\exists u: (u \in z) \land (y = G(u))) \) den String \( ((y \in z) \land F(y)) \) enthält. Dabei ist \(F(y)\) eine Aussage, die \(x\) nicht enthält.
Wie eng ist der Zusammenhang zwischen diesen beiden Axiomen? Versuchen wir einmal, eine beliebige Eigenschaft \(F\) durch die Festlegung einer dazu passenden Abbildung \(G\) gleichsam zu modellieren. Dies gelingt so:
Die Abbildung \(G\) erzeugt damit aus jedem Element \(u\) ein neues Element \( y = G(u) \), das auf jeden Fall die Aussage \(F(y)\) erfüllt, für das also die Aussage \(F(y)\) aus den Axiomen ableitbar (beweisbar) ist.
Ein Abbild \(G(u)\) zu sein bedeutet für dieses spezielle \(G\) dasselbe wie die Bedingung \(F\) zu erfüllen (wobei wir hier auf eine detaillierte Begründung verzichten wollen). Jede Bedingung \(F\) lässt sich also durch eine geeignete Abbildung \(G\) modellieren. Insofern ist die Menge \(x\), deren Existenz aufgrund des Ersetzungsaxioms über eine entsprechend gewählte Abbildung \(G\) gesichert ist, genau gleich der Menge \(x\), die durch das Aussonderungsaxiom über eine Eigenschaft \(F\) gebildet wird.
Das einzige Problem könnte dann entstehen, wenn es kein Element \(e\) in der Menge \(z\) gibt, so dass \(F(e)\) ableitbar ist. Das Aussonderungsaxiom liefert dann für \(x\) die leere Menge \( \varnothing \). Das Ersetzungsaxiom kann dagegen die Existenz der leeren Menge nicht beweisen, d.h. deren Existenz muss als Axiom separat gefordert werden.
Fast jede Instanz des Aussonderungsaxioms (gegeben durch ein \(F\)) kann also aus einer geeigneten Instanz des Ersetzungsaxioms hergeleitet werden, indem man die Abbildung \(G\) geeignet wählt, so dass sie \(F\) modelliert. Die einzige Instanz des Aussonderungsaxioms, bei der das nicht geht, liegt vor, wenn die Eigenschaft \(F\) für kein Element von \(z\) ableitbar ist. In diesem Fall ist \(x\) gleich der leeren Menge.
Man lässt deshalb häufig das Aussonderungsaxiom ganz weg und wählt nur das Ersetzungsaxiom sowie das Axiom von der Existenz der leeren Menge als Grundaxiome, da sich aus diesen beiden das Aussonderungsaxiom ergibt. Wir haben das Aussonderungsaxiom dennoch als Axiom separat hinzugenommen, da es sehr nützlich zum Vergleich mit dem uneingeschränkten Komprehensions-Axiom ist. Erst so versteht man, wie Cantors Mengenlehre modifiziert wurde, um Russels Widerspruch zu verhindern.
Das Aussonderungsaxiom hat es uns ermöglicht, über eine Eigenschaft \(F(y)\) alle die Elemente \(y\) einer Menge \(z\) zu einer neuen Menge \(x\) zusammenzufassen, die \(F(y)\) erfüllen. Damit war es möglich, Teilmengen (Untermengen) einer vorhandenen Menge zu konstruieren.
Für die Mathematik benötigt man jedoch noch eine weitergehende Möglichkeit: man benötigt die Menge aller Teilmengen zu einer vorgegebenen Menge. Diese Menge bezeichnet man auch als Potenzmenge.
Ein Beispiel:
Schauen wir uns die Menge \( \{1,2,3\} \) an. Die Potenzmenge dieser Menge lautet
\[
\left\{ \, \varnothing, \{1\}, \{2\}, \{3\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\} \, \right\}
\]
In der Potenzmenge sind alle Mengen enthalten, die sich aus den Elementen \(1, 2\) und \(3\) der vorgegebenen
Menge bilden lassen. Dabei legen wir fest, dass auch die leere Menge \( \varnothing \) dazugehört,
ebenso wie die komplette Menge.
Bildet man die Potenzmenge einer Menge aus \(n\) Elementen, so enthält diese Potenzmenge allgemein \(2^n\) Elemente, denn so viele verschiedene Mengen lassen sich aus \(n\) Elementen bilden (Begründung folgt gleich). Das erklärt dann auch die Bezeichnung Potenzmenge, denn aus \(n\) wird \(2^n\). Im obigen Fall enthält die Potenzmenge der 3-Elemente-Menge also \(2^3 = 8\) Elemente (Mengen).
Warum das so ist, kann man relativ einfach einsehen, wenn man sich von einer Menge mit \(n\) Elementen zu einer Menge mit \(n+1\) Elementen vortastet. Dazu bezeichnen wir die Anzahl der Teilmengen einer \(n\)-Element-Menge mit \(N_n\) und fragen uns, wieviele Teilmengen hinzukommen, wenn wir ein Element (nennen wir es \(e\) ) zur \(n\)-Element-Menge hinzufügen. Alle Teilmengen, die \(e\) nicht enthalten, können wir bereits aus der \(n\)-Element-Menge bilden. Bei Hinzunahme von \(e\) können wir zu jeder dieser Teilmengen eine weitere Teilmenge bilden, die zusätzlich \(e\) enthält, und erhalten damit alle Teilmengen der um \(e\) vergrößerten Menge. Das Hinzufügen eines Elementes verdoppelt also die Zahl der Teilmengen, die gebildet werden können, d.h. es gilt \( N_{n+1} = 2 N_n \). Nun müssen wir nur noch den Startpunkt finden: Wieviele Teilmengen lassen sich bei einer Menge mit nur einem Element bilden (wir schreiben diese Menge als \( \{a\} \) )? Es sind zwei Teilmengen, nämlich die leere Menge \( \varnothing \) und die Menge \( \{a\} \) selbst. Also ist \( N_1 = 2 \), und damit ist \( N_n = 2^n \) .
Bei unendlichen Mengen ist die Sache komplizierter. So ist die Potenzmenge einer abzählbaren Menge nicht abzählbar und in diesem Sinn mächtiger als die Ausgangsmenge.
Warum man Potenzmengen benötigt, wird klar, wenn man die Menge aller reellen Zahlen beschreiben möchte. Eine reelle Zahl können wir generell als Binärstring schreiben, also z.B. als \[ 0,10101100110000101110 ... \] d.h. diese Zahl ist gleich \(1/2 + 1/8 + 1/32 + 1/64 + ... \) . Wie können wir diese Zahl durch eine Menge darstellen, wenn wir voraussetzen, dass wir die natürlichen Zahlen bereits konstruiert haben? Eine Möglichkeit besteht darin, einfach die Stellen anzugeben, an denen hinter dem Komma eine 1 steht: \[ \{ 1, 3, 5, 6, 9, 10, 15, 17, 18, 19, ... \} \] (wir wollen uns hier auf positive reelle Zahlen unterhalb von Eins beschränken).
Wie wir sehen, entspricht in diesem Sinn jede reelle Zahl einer endlichen oder unendlichen Menge natürlicher Zahlen, durch die sie eindeutig dargestellt werden kann. Umgekehrt führt jede Menge natürlicher Zahlen auf diese Weise zu einer reellen Zahl.
Wenn wir nun von der Menge aller reellen Zahlen sprechen wollen, so benötigen wir die Menge aller Mengen, die sich aus natürlichen Zahlen bilden lassen. Anders ausgedrückt: Wir brauchen die Menge aller Teilmengen der natürlichen Zahlen, also die Potenzmenge der natürlichen Zahlen.
Die Existenz einer Potenzmenge lässt sich aus den bisherigen Axiomen nicht ableiten. Daher benötigen wir das folgende Axiom:
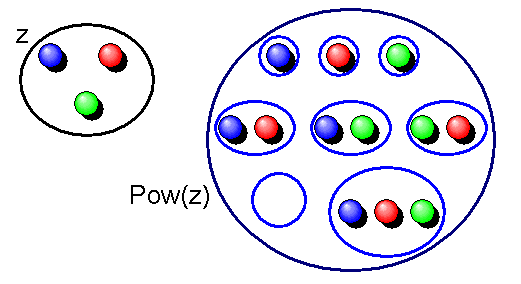
Dabei ist \(z\) die vorgegebene Menge und \(x\) die Potenzmenge, deren Existenz im Axiom mit \( \exists x \) gefordert wird. Die Potenzmenge \(x\) besteht dabei aus gewissen Mengen \(y\), wie man an \( (y \in x) \) erkennt. Diese Mengen \(y\) sind genau dann Elemente der Potenzmenge \(x\), wenn sie Teilmengen von \(z\) sind (was der Ausdruck rechts von \( \Leftrightarrow \) bedeutet), wobei auch die leere Menge \( \varnothing \) für \(y\) erlaubt ist, ebenso wie die Menge \(z\) selbst.
Das Axiom sagt also, dass es zu jeder Menge \(z\) eine Potenzmenge \(x\) gibt, die alle Teilmengen von \(z\) enthält. Mit anderen Worten:
Man schreibt auch \( x = \mathcal{P}(z) \).
Das Potenzmengenaxiom ist wie das Vereinigungsaxiom und das Ersetzungsaxiom wieder eine spezielle Version des uneingeschränkten Komprehensions-Axiomenschemas \[ \exists x: \forall y : \, [ (y \in x) \Leftrightarrow F(y) ] \] Setzen wir hier für \(F(y)\) die spezielle Aussage \( \forall u : \, (u \in y) \Rightarrow (u \in z) \) ein (d.h. \(y\) ist eine Teilmenge von \(z\) )und stellen \( \forall z \) voran, so erhalten wir das Potenzmengenaxiom.
Das Potenzmengenaxiom ist ein sehr starkes Axiom mit weitreichenden Folgen. Es erlaubt die Konstruktion verschieden mächtiger unendlich großer Mengen: Cantor hat gezeigt, dass es für keine Menge \(z\) eine eins-zu-eins-Zuordnung von \(z\) nach \( \mathcal{P}(z) \) gibt, ohne dass Elemente von \( \mathcal{P}(z) \) übrig bleiben, d.h. Potenzmengen sind in diesem Sinn mächtiger als ihre Ausgangsmengen (auch bei unendlich großen Ausgangsmengen). Das gilt auch für Potenzmengen von Potenzmengen – das Spiel lässt sich unendlich weit fortsetzen. Letztlich folgt daraus auch die Überabzählbarkeit der reellen Zahlen.
Die bisherigen Axiome schließen Mengen, die sich selbst enthalten (z.B. eine Menge \(x\) mit \( x \in x \) ), nicht aus. Ebenfalls denkbar sind zyklische Ketten von \( \in \) -Beziehungen: \( x \in y \) und zugleich \( y \in x \) . Solche Mengen passen nicht zu der angestrebten Interpretation des \( \in \) -Symbols, das wir ja als "ist Element von" oder als "ist enthalten in" interpretieren wollen. Aus diesem Gund führte von Neumann im Jahr 1925 das folgende Axiom ein:
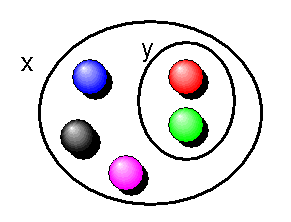
Wieder einmal sieht dieses Axiom zunächst sehr komplex aus, da es mit den wenigen zur Verfügung stehenden Mitteln der formalen Sprache der Mengenlehre und der Logik ausgedrückt werden muss. Wir wollen es daher in eine verständlichere Sprache übersetzen.
Der Anfang \( \forall x \) sagt, dass das Axiom für jede beliebige Menge gelten soll. Alle Mengen müssen regulär sein, so wie es das Axiom festlegt.
Die erste Klammer \( [\exists u: u \in x] \) vor dem ersten Pfeil ( \( \Rightarrow \) ) bedeutet: "Wenn \(x\) nicht die leere Menge ist (d.h. wenn es (mindestens) ein Element \(u\) enthält), ... ".
Hinter dem ersten Pfeil ( \( \Rightarrow \) ) folgt dann der "dann-Teil". Dieser sagt, dass die Menge \(x\) dann ein Element \(y\) enthalten muss (ist ja klar, wenn sie nicht leer ist), und dass für dieses Element \(y\) etwas gilt, nämlich \( (\, \forall z : \, (z \in y) \Rightarrow (\neg (z \in x)) \, ) \). Das bedeutet, dass kein Element \(z\) in diesem \(y\) zugleich Element der nächsthöheren Menge \(x\) sein darf (die Schnittmenge von \(y\) und \(x\) ist also leer). Die Elemente von mindestens einem Element \(y\) in der Menge \(x\) dürfen also nicht selbst Elemente von \(x\) sein.
Das Axiom sagt also:
Um das Axiom richtig zu verstehen, schauen wir uns eine seiner Auswirkungen an:
Nehmen wir an, es gäbe eine Menge \(x\), die sich selbst enthält (also \(x \in x\) ). Das Paarbildungsaxiom sagt nun, dass es zu \(x\) eine Menge \( \{ x \} \) gibt, die die Menge \(x\) als Element enthält. Das Regularitätsaxiom fordert nun in diesem \( \{ x \} \) die Existenz mindestens eines besonderen Elementes \(y\), das in diesem speziellen Fall gleich \(x\) sein muss (denn andere Elemente enthält \( \{ x \} \) nicht). Kein Element von diesem besonderen \(y\) (also hier von \(x\) ) darf nach dem Regularitätsaxiom in \( \{ x \} \) vorkommen. Nun enthält aber \(x\) sich selbst als Element, d.h. \(x\) enthält wegen \(x \in x\) ein Element (nämlich \(x\) ), das in \( \{ x \} \) vorkommt. Das Regularitätsaxiom führt also bei Mengen, die sich selbst enthalten, zu einem Widerspruch und verhindert damit die Existenz solcher Mengen.
Analog lassen sich auch Mengen \(x\) und \(y\) ausschließen, die sich gegenseitig als Element enthalten: \( x \in y \) und zugleich \( y \in x \) ist nicht erlaubt.
Letztlich bewirkt das Regularitätsaxiom, dass es Mengen unterschiedlicher Stufe gibt. Eine Menge \(x\), die eine Menge \(y\) enthält, besitzt eine höhere Stufe als \(y\). Nichtleere Mengen höhere Stufe besitzen immer eine Menge niederer Stufe als Element, so dass diese Menge niederer Stufe komplett (d.h. in jedem Element) anders ist als die Menge höherer Stufe.
Kommen wir nun zum letzten Axiom: dem Auswahlaxiom. Cantor selbst hat dieses Axiom nie explizit formuliert, sondern eher intuitiv seine Richtigkeit vorausgesetzt.
In seiner strengen Version in der formalen Sprache der Mengenlehre ist dieses Axiom ziemlich kompliziert, so dass wir das Axiom hier nur mit Worten wiedergeben wollen:
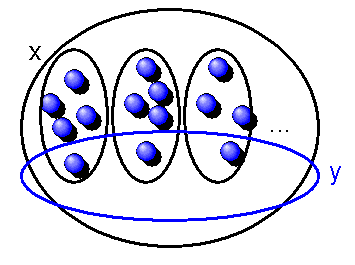
Die Menge \(y\) fischt also aus den in \(x\) enthaltenen Mengen jeweils genau ein Element heraus. Das Axiom sagt also, dass man aus jeder Menge einer beliebig vorgegebenen Ansammlung von Mengen jeweils ein Element aus jeder Menge herausnehmen kann. Dabei sagt das Axiom nur, dass es geht (d.h. die Menge \(y\) existiert), aber es sagt nicht, wie es geht. Das Axiom ist also nicht konstruktiv. Man kann es nicht zur Konstruktion der auswählenden Menge \(y\) verwenden, d.h. diese Menge bleibt gleichsam dunkel. Dasselbe gilt dann für alle Schlussfolgerungen, die man aus diesem Axiom zieht. Diese Schlussfolgerungen werden oft nur sagen, dass etwas geht, aber nicht unbedingt, wie. Daher ist das Auswahlaxiom nicht unumstritten, obwohl es intuitiv mit unserer Vorstellung von Mengen übereinstimmt.
Das Auswahlaxiom wird nur deshalb benötigt, weil wir unendliche Mengen zugelassen haben. Für endliche Mengen wird es nicht benötigt. Damit überträgt das Auswahlaxiom unsere intuitive Vorstellung, dass man aus Mengen einzelne Elemente herausnehmen kann, von den endlichen Mengen auf die unendlichen Mengen (bei denen unsere Vorstellungskraft allerdings ihre Grenzen hat). In der Mathematik wird das Auswahlaxiom oft intuitiv verwendet, ohne dass man sich dessen bewusst ist. So wird es beispielsweise benötigt, um zu beweisen, dass jeder Vektorraum eine Basis hat.
Wir sind in Kapitel 3.2 bereits auf die Probleme eingegangen, die entstehen, wenn man nach der Wahrheit des Auswahlaxioms fragt. Ein Beispiel: Nehmen wir für \(x\) die Menge aller nichtleeren Teilmengen der reellen Zahlen. Das Axiom behauptet nun, dass man aus jeder dieser Teilmengen ein Element auswählen kann. Aber wie soll das gehen? Kann man z.B. die kleinste reelle Zahl in jeder dieser Teilmengen nehmen? Leider gibt es Mengen, die keine kleinste Zahl enthalten, z.B. die Menge aller positiven reellen Zahlen (ohne Null). Auch andere Methoden haben ihre Probleme. Man findet keine offensichtliche Methode, mit der man aus jeder Teilmenge der reellen Zahlen eine davon auswählen kann.
Ob man das Auswahlaxiom intuitiv akzeptiert oder nicht, hängt damit zusammen, was man unter der Existenz eines Objektes versteht. Was bedeutet es, wenn wir das formale "es gibt", also \( \exists \) , verwenden? Akzeptiert man das Auswahlaxiom, so geht man davon aus, dass ein Objekt existiert, wenn die Annahme seiner Existenz zu keinem Widerspruch führt. Existenz bedeutet also hier Verträglichkeit. Man bezeichnet diese Interpretation auch als schwachen Existenzbegriff. Im Vergleich dazu fordert der starke Existenzbegriff, dass ein Objekt nur dann existiert, wenn es sich auch konstruieren lässt. Existenz bedeutet dann Konstruierbarkeit.
Dass das Auswahlaxiom verträglich mit den anderen Axiomen der Mengenlehre ist, bewies Kurt Gödel im Jahr 1938. Er zeigte: wenn es Widersprüche in der Mengenlehre gibt, so gibt es diese auch dann, wenn man das Auswahlaxiom weglässt.
Es ist möglich, andere Axiome als das Auswahlaxiom in der Mengenlehre zu verwenden. Insofern hat das Auswahlaxiom eine gewisse Ähnlichkeit mit dem Parallelenaxiom der Geometrie (siehe Kapitel 2.1). Ein Beispiel dafür ist das Axiom der abhängigen Auswahlen, das 1942 von Paul Bernays formuliert wurde. Es sagt, dass man eine abzählbare Zahl von Elementen aus jeder Menge eines vorgegebenen Mengensystems auswählen kann, wobei jede Auswahl von der vorhergehenden Auswahl abhängt. Ein anderes Beispiel ist das Axiom der Determiniertheit. Solche Axiome sind beispielsweise in der mathematischen Spieltheorie nützlich.
Damit haben wir die komplette formale Sprache der Zermelo-Fränkel-Mengenlehre zusammen. Sie besteht aus den Syntaxregeln der Logik erster Ordnung inklusive der Zeichen \( \forall , \exists , \Rightarrow , \Leftrightarrow , \neg \) , aus Variablen wie \(x\), \(y\) etc. sowie aus den beiden Prädikaten \( \in , = \) . Hinzu kommen als Start-Zeichenketten die oben dargestellten Zermelo-Fränkel-Axiome.
Man kann zwar nicht beweisen, dass dieses formale System widerspruchsfrei ist (zumindest kann man dies nicht innerhalb des Systems beweisen), aber man hat seit einem dreiviertel Jahrhundert keine Widersprüche finden können. Außerdem hat sich das Axiomensystem als sehr stabil und tragfähig erwiesen. Seit 1925 wurde kein weiteres Axiom gefunden, das die Konstruktion weiterer Mengen ermöglichen würde. Zumindest hinsichtlich der Konstruktion von Mengen (also hinsichtlich nützlicher Versionen des Komprehensions-Axioms mit entsprechenden Eigenschaften \(F(y)\) ) scheint das System also recht vollständig zu sein. Was die reine Existenz von Mengen betrifft, so sind hingegen weitere Axiome durchaus denkbar (wir werden im nächsten Kapitel noch darauf zurückkommen). Das bedeutet, dass die Annahme der Existenz weiterer Mengen nicht zu einem Widerspruch führt, wobei wir aus der Existenzannahme keine Konstruktionsvorschrift ableiten können.
Die formale Sprache der Zermelo-Fränkel-Mengenlehre ermöglicht es nun, praktisch die gesamte Standard-Mathematik darzustellen (zumindest aber das, was in der Mathematik explizit konstruierbar ist). Ein Teil von Hilberts Vision lässt sich also tatsächlich durchführen: "Übersetze die gesamte Mathematik in ein formales System". Dabei besitzt diese formale Sprache nur einen sehr geringen Wortschatz. Sie ist wie die Maschinensprache eines Computerprozessors. Jeder denkbare Algorithmus lässt sich in diese Maschinensprache übersetzen, genauso, wie sich jedes mathematische Konstrukt in der Sprache der Mengenlehre ausdrücken lässt.
Leider sehen die entsprechenden Ausdrücke zumeist sehr lang und unübersichtlich aus (ganz analog zu Programmen in Maschinensprache). Die obigen Axiome vermitteln bereits einen ersten Eindruck davon. Kaum ein Mathematiker arbeitet daher direkt in der formalen Sprache der Mengenlehre. Stattdessen verwendet man höhere Sprachformen, genauso wie man auch höhere Programmiersprachen verwendet.
Wir wollen uns daher zumindest ansatzweise ansehen, wie man auf der Grundlage der Mengenlehre in der Mathematik eine solche höhere Sprache aufbauen kann. Diese höhere Sprache soll alle in der Mathematik gebräuchlichen Begriffe wie Zahlen, Abbildungen, Relationen etc. enthalten.
Betrachten wir als erstes Beispiel die leere Menge \( \varnothing \) . Leider enthält unsere formale Sprache der Mengenlehre keine Konstanten. Wir können aber bestimmte Zeichenketten der formalen Sprache durch einen entsprechenden zusammenfassenden Platzhalter ersetzen, wobei wir diese Ersetzung jederzeit wieder rückgängig machen können.
Wie würde das bei dem Zeichen \( \varnothing \) für die leere Menge konkret funktionieren? Angenommen, wir würden eine Aussage \( F(\varnothing) \) über die leere Menge hinschreiben. Was soll sie bedeuten, wenn doch das Zeichen \( \varnothing \) in der strengen formalen Sprache der Zermelo-Fränkel-Mengenlehre nicht existiert? Nun, wir sagen einfach, dass \( F(\varnothing) \) ein Platzhalter ist, den wir jederzeit durch die folgende Zeichenkette ersetzen können: \[ \forall x: \, [ \, ( \forall y : \, \neg (y \in x) ) \Rightarrow F(x) \, ] \] Darin taucht die formale Aussage \(F\) erneut auf, aber diesmal für die Menge \(x\). Die Aussage sagt, dass für jedes \(x\), das die leere Menge ist (weil es keine Elemente \(y\) enthält), die Aussage \(F(x)\) gilt. Die Aussage \(F(x)\) gilt also für die leere Menge, was wir abgekürzt als \( F(\varnothing) \) schreiben wollen.
Überall, wo wir in Zukunft einen Ausdruck \(F(\varnothing)\) schreiben, können wir ihn jederzeit durch die obige Zeichenkette ersetzen und ihn so in die formale Sprache der Mengenlehre zurückübersetzen. So ist der Ausdruck \( \exists \varnothing \) (also "es gibt die leere Menge") einfach nur ein Platzhalter für den formalen Ausdruck \[ \forall x: \, [ \, ( \forall y : \, \neg (y \in x) ) \Rightarrow \exists x \, ] \] den man umwandeln kann in den Ausdruck \[ \exists x: [\forall y : \, \neg (y \in x)] \]
Analog kann man auch für weitere Mengen Abkürzungen einführen, beispielsweise die bekannte Schreibweise \( \{ a, b \} \) für die Menge, die die Elemente \(a\) und \(b\) enthält. Und auch für Mengenoperationen wie die Vereinigung von Mengen kann man Abkürzungen einführen, die sich jederzeit zurückübersetzen lassen. Die Details wollen wir hier überspringen und statt dessen direkt zu der in der Mathematik üblichen Mengenschreibweise übergehen.
Die Elemente in Mengen sind ungeordnet. So sind die Elemente \(x\) und \(y\) in der Menge \( \{x, y\} \) ungeordnet: \( \{x, y\} \) bedeutet dasselbe wie \( \{y, x\} \). Es kommt ja beim Symbol \( \in \) nur darauf an, ob etwas Element einer Menge ist oder nicht.
Man benötigt in der Mathematik aber auch geordnete Paare wie \( (x, y) \), bei denen \( (x, y) \) nicht dasselbe wie \( (y, x) \) ist. Statt dessen sollen zwei geordnete Paare \( (a, b) \) und \( (c, d) \) genau dann gleich sein, wenn \(a = c\) und \(b = d\) ist. Dies erreichen wir, wenn wir \( (x, y) \) als Abkürzung für die Menge \( \{ \{x\}, \{x,y\} \} \) ansehen:
Mit Hilfe des geordneten Paares kann man nun auch den Begriff des karthesischen Produktes \( A \times B \) zweier Mengen \(A\) und \(B\) definieren, also die Menge der entsprechenden geordneten Paare der Elemente beider Mengen (wobei auch \(A = B\) erlaubt ist):
Dieses karthesische Produkt kann man nun wiederum verwenden, um Relationen zwischen zwei Mengen \(A\) und \(B\) zu definieren:
Um eine Relation \(R\) festzulegen, muss man also eine Teilmenge von \( A \times B \) festlegen. Oft verwenden wir für die Elemente der Menge \(R\) die Schreibweise \( R(a,b) \) als Abkürzung für \( (a, b) \in R \) . Wir werden später noch Beispiele für Relationen kennenlernen. So werden wir gleich noch eine Relation sehen, die \( a \le b \) bedeutet.
Falls es bei einer Relation für jedes \(x\) aus einer Menge \(X\) genau ein \(y\) aus einer Menge \(Y\) gibt, so dass \(R(x,y)\) gilt (d.h. \( (x,y) \in R \) ), dann bezeichnet man eine solche Relation auch als Funktion. Statt \(R(x,y)\) schreibt man dann auch \(y=f(x)\). So definiert die Relation \( R = \{ (1,2) , (2,4) , (3,6), ... \} \) beispielsweise eine Funktion, die natürliche Zahlen verdoppelt (wobei wir den Begriff der natürlichen Zahl erst noch auf Basis der Mengenlehre definieren müssen – kommt gleich).
Mithilfe spezieller Relationen können wir den Begriff von Ordnungen auf Mengen definieren. Die Kleiner-Gleich-Beziehung zwischen Zahlen ist eine solche Ordnung, ebenso wie die alphabetische Anordnung bei Zeichenketten.:
Diese Definition sieht relativ abstrakt aus, aber wenn man sich für \(R(x,y)\) Aussagen wie \(x ≤ y\) oder "\(x\) steht an der Stelle oder links von \(y\) " denkt, so versteht man den Sinn dieser Definition (z.B. folgt wegen Punkt 3 (Transitivität) aus \(x \le y\) und \(y \le z\), dass auch \(x \le z\) sein muss).
Wenn bei einer Ordnung \(R\) zusätzlich auch noch für alle \(x\) und \(y\) aus \(X\) entweder \(R(x,y)\) oder \(R(y,x)\) gilt (d.h. man kann zwei beliebige Elemente hinsichtlich ihrer Ordnung vergleichen), so nennt man die Ordnung linear oder total. Andernfalls handelt es sich um eine partielle Ordnung (auch Halbordnung genannt).
Um diese Begriffe besser zu verstehen, wollen wir uns einige Beispiele ansehen (wobei wir den Begriff der Zahl erst später genau definieren werden):
Es gibt noch eine wichtige spezielle Ordnung auf einer Menge: die Wohlordnung.
So ist die übliche kleiner-gleich-Beziehung eine Wohlordnung auf den natürlichen Zahlen, nicht aber auf den reellen Zahlen. Beispielsweise haben die positiven reellen Zahlen ohne Null kein kleinstes Element – man kann zwar beliebig nahe an die Null herangehen, aber es gibt immer eine noch kleinere positive reelle Zahl.
Wohlordnungsprinzip:
Man kann mit Hilfe der Zermelo-Fränkel-Axiome inklusive Auswahlaxiom zeigen, dass
jede Menge eine Wohlordnung besitzt. Man nennt dies auch das Wohlordnungsprinzip.
Man kann sogar das Auswahlaxiom durch das Wohlordnungsprinzip ersetzen. Die entsprechenden
Axiomensysteme sind gleichwertig! Dies kann man auch anschaulich verstehen, denn wenn es nach dem
Wohlordnungsprinzip ein kleinstes Element in jeder Teilmenge einer Menge gibt, so
kann man ja gerade dieses auswählen.
Allerdings hat das Wohlordnungsprinzip dieselben Probleme wie das Auswahlaxiom: es behauptet lediglich die Existenz einer Wohlordnung für jede Menge, sagt aber nicht, wie diese konstruiert werden kann. Die Annahme einer Wohlordnung auf jeder Menge ist also mit den anderen Axiomen verträglich (existiert also im Sinn des schwachen Existenzbegriffs), kann aber nicht immer konstruiert werden. Beispielsweise ist keine Wohlordnung auf den reellen Zahlen bekannt (die übliche kleiner-gleich-Beziehung ist keine Wohlordnung auf den reellen Zahlen, wie wir oben bereits gesehen haben).
Transfinite Induktion:
Das Wohlordnungsprinzip macht jede beliebige Menge einer speziellen Beweistechnik zugänglich,
die transfinite Induktion genannt wird.
Wenn man zeigen will, dass eine Aussage \(P\) für alle Elemente einer Menge gilt,
dann beweist man \(P\) zunächst für das kleinste (oder besser: erste) Element,
und zeigt dann, dass für \(a \le b\) (d.h. \(R(a,b)\) gilt) aus \(P(a)\) auch \(P(b)\) folgt.
Wie bei einer umfallenden Dominokette (ggf. mit Verzweigungen) überträgt sich dann
die Aussage \(P\)
ausgehend vom ersten Element auf alle Elemente der Menge.
Der nächste Schritt besteht nun darin, die natürlichen Zahlen in der Sprache der Mengenlehre zu konstruieren. Als Basis dafür haben wir lediglich die leere Menge als einziges Urelement zur Verfügung sowie die übrigen Axiome der Mengenlehre. Mit diesen Werkzeugen müssen wir nun also versuchen, neue Mengen zu konstruieren, die sich wie natürliche Zahlen verhalten. Als Leitfaden dafür, was natürliche Zahlen sein sollen, verwenden wir dabei die Peano-Axiome aus Kapitel 2.1 .
Beginnen wir mit der leeren Menge \( \varnothing \). Um Anschluss an die gewohnten Zahlensymbole zu bekommen, wollen wir diese Menge mit dem Zahlzeichen \(0\) (Null) bezeichnen: \[ 0 := \varnothing \] Das passt auch dazu, dass die leere Menge selbst null Elemente enthält.
Um von Null ausgehend zu den weiteren Zahlen zu gelangen, benötigen
wir eine Nachfolger-Funktion, die zu jeder vorgegebenen natürlichen Zahl (repräsentiert
durch die entsprechende Menge) eine eindeutige Nachfolger-Menge
angibt. Versuchen wir es mit der folgenden Definition:
\[
n^* = n \cup \{n\}
\]
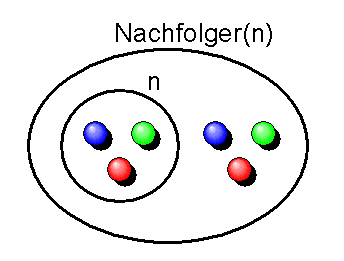
Dabei ist \(n^*\) der Nachfolger von \(n\), und \( n \cup \{n\} \) ist die Menge, die alle Elemente von \(n\) und als zusätzliches Element die Menge \(n\) selbst enthält. Damit enthält \(n^*\) genau ein Element mehr als \(n\), nämlich die Menge \(n\) selbst als neues Element.
Diese Konstruktion dieser Vereinigungsmenge ist aufgrund der Zermelo-Fränkel-Axiome möglich, denn das Paarbildungsaxiom erlaubt die Konstruktion von \(\{n\}\) und anschließend von \( \{n, \{n\} \} \), und das Vereinigungsaxiom ermöglicht anschließend die Bildung der Vereinigungsmenge der beiden Teilmengen \(n\) und \(\{n\}\).
Wenn wir nun \(1 := 0^*\) setzen, \(2 := 1^*\) usw., so ergibt sich
die folgende Darstellung der natürlichen Zahlen:
\begin{align}
0 &:= \varnothing \\
1 &:= \{ \varnothing \} = \{ 0 \} \\
2 &:= \{ \varnothing , \{ \varnothing \} \} = \{ 0, 1 \} \\
3 &:= \{ \varnothing , \{ \varnothing \}, \{ \varnothing , \{ \varnothing \} \} \} = \{ 0, 1, 2 \} \\
& ...
\end{align}
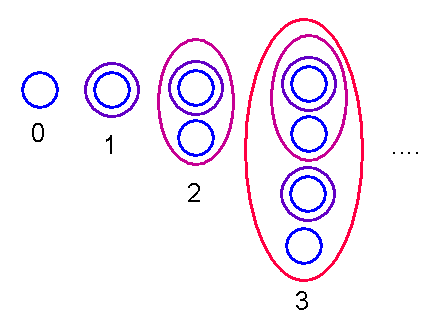
Man kann nun mit Hilfe des Unendlichkeitsaxioms und der anderen Axiome zeigen, dass sich die Menge all dieser Mengen konstruieren lässt (der Beweis ist allerdings nicht ganz einfach). Nennen wir diese Menge \( \mathbb{N} \), d.h. \begin{align} \mathbb{N} &= \{ 0, 1, 2, 3, ... \} = \\ &= \{ \varnothing , \{ \varnothing \} , \{ \varnothing , \{ \varnothing \} \} , ... \} \end{align} oder präziser: \begin{align} & \mathbb{N} := \{ \, n \, ; \; \forall w : \, [ \, ( \varnothing \in w ) \, \land \\ \forall y &: \, ( y \in w \Rightarrow y \cup \{y\} \in w) \Rightarrow n \in w \, ] \, \} \end{align} Diese komplizierte Definition sagt: Man betrachte als Quelle der Elemente \(n\) alle Mengen \(w\), die die leere Menge \( \varnothing \) enthalten und die ansonsten so gebaut sind, dass sie zu jedem Element \(y\) auch \( y \cup \{y\} \) enthalten. Ein Beispiel dafür ist die Menge \[ w = \{ \varnothing, \{\varnothing\}, \{\varnothing,\{\varnothing\}\}, ..., \{\varnothing,\{\varnothing,\{\varnothing\}\}\}, ... \} \] Das Element \( \{\varnothing,\{\varnothing,\{\varnothing\}\}\} = \{0, 2\} \) stört allerdings noch, denn es soll nicht in der Menge \( \mathbb{N} \) enthalten sein. Daher wird noch die Schnittmenge aller Mengen \(w\) gebildet, d.h. es werden nur diejenigen Elemente nach \( \mathbb{N} \) übernommen, die in allen Mengen \(w\) vorkommen. Dabei fliegen alle Elemente heraus, die nicht aufbauend auf der leeren Menge \( \varnothing \) gebildet werden können.
Ob die Elemente von \( \mathbb{N} \) sich tatsächlich wie natürliche Zahlen verhalten, müssen wir nun noch nachweisen. Dazu wollen wir uns noch einmal die Peano-Axiome aus Kapitel 2.1 ansehen, so wie wir sie in der formalen Sprache der Peano-Arithmetik formuliert haben:
Wir wollen diese Axiome auf die folgende Weise in die Sprache der Mengenlehre übersetzen: \begin{align} & 0 \in \mathbb{N} \\ & \forall n: \, (n \in \mathbb{N} ) \Rightarrow ( n^* \in \mathbb{N} ) \\ & \forall n: \, (n \in \mathbb{N} ) \Rightarrow \neg( n^* = 0 ) \\ & \forall n, m: \,[ \, (m, n \in \mathbb{N} ) \, \land \, ( m^* = n^* ) \, ] \Rightarrow [m = n] \\ & \forall A: \, [ \, (0 \in A) \, \land \, \forall n : \, [(n \in \mathbb{N}) \Rightarrow \\ & \quad \quad \quad ( (n \in A) \Rightarrow ( n^* \in A)) \, ]] \Rightarrow [ \mathbb{N} \subseteq A ] \end{align} Wie wir sehen, erfassen die neuen mengentheoretischen Aussagen den beabsichtigten Sinn der Peano-Axiome. Neu ist dabei die Aussage \( 0 \in \mathbb{N} \) – dieses Axiom gab es in der formalen Sprache der Peano-Arithmetik gar nicht, denn die Aussage " \( 0 \) (also Null) ist eine natürliche Zahl" lässt sich in dieser Sprache gar nicht ausdrücken. In der Peano-Arithmetik entspricht die Aussage \( 0 \in \mathbb{N} \) einfach der Tatsache, dass \(0\) eine Konstante im Wortschatz dieses formalen Systems ist.
Weiter beobachten wir, dass der Ausdruck \( \forall n : \) aus der Peano-Arithmetik ergänzt wird durch den Ausdruck \( (n \in \mathbb{N} ) \Rightarrow \). Diese Einschränkung des Variablenbereichs auf die Elemente der Menge \( \mathbb{N} \) ist auch notwendig, denn die Aussage gilt nicht für alle Mengen \(n\), sondern nur für die Mengen, die natürliche Zahlen darstellen sollen. In der Sprache der Mengenlehre stehen die Variablen ja für alle möglichen Mengen und nicht nur für natürliche Zahlen wie in der Peano-Arithmetik beabsichtigt.
Nun sind die obigen Aussagen in der Mengenlehre natürlich keine Axiome mehr, sondern sie müssen aus den Zermelo-Fränkel-Axiomen und der obigen Konstruktion der Menge \( \mathbb{N} \), der Menge \(0\) und der Nachfolger-Funktion abgeleitet werden. Wir wollen diesen Beweis hier überspringen und nur mitteilen, dass er geführt werden kann. Und weil das so ist, sind wir berechtigt, die obige Mengenkonstruktion als ein Modell für die natürlichen Zahlen in der Sprache der Mengenlehre anzusehen. Dieses Modell wird auch als von Neumannsches Modell bezeichnet.
Um den mengentheoretischen Aufbau der natürlichen Zahlen abzuschließen, müssen wir zusätzlich noch die Addition und die Multiplikation auf die Sprache der Mengenlehre zurückführen. Dazu definiert man über den Relationsbegriff Addition und Multiplikation als Funktionen von der Menge \( \mathbb{N} \times \mathbb{N} \) nach \( \mathbb{N} \), wobei die vier aus Kapitel 2.1 bekannten Aussagen gelten:
Wir wollen hier darauf verzichten, genauer ins Detail zu gehen.
Man kann die so definierte Addition dazu benutzen, um eine Ordnung auf der Menge \( \mathbb{N} \) zu definieren. Dazu definieren wir die folgende Relation \( R_\le \) : \begin{align} & R_\le := \{ \, (m, n) \in \mathbb{N} \times \mathbb{N} \, ; \\ & \quad \exists k: (k \in \mathbb{N}) \land (m + k = n) \, \} \end{align} Wir schreiben auch kurz \(m \le n\), wenn es ein \(k\) aus \( \mathbb{N} \) gibt mit \(m + k = n\) . \( \mathbb{N} \) umfasst dabei auch die Null.
Man kann nun zeigen, dass es sich bei \( R_\le \) um eine lineare (also totale) Ordnung handelt, d.h. es gilt für alle \(m, n\) aus \( \mathbb{N} \) immer \(m \le n\) oder \(n \le m\). Es handelt sich sogar um eine Wohlordnung, d.h. jede Teilmenge von \( \mathbb{N} \) hat ein kleinstes Element bezüglich der \( \le \) -Relation.
Die in die Sprache der Mengenlehre übersetzten Peano-Axiome sehen so aus, als ob sie genau dasselbe bedeuten wie die ursprünglichen Peano-Axiome. Dennoch sehen sie im Detail anders aus, denn sie sind keine Axiome der Peano-Arithmetik mehr, sondern wohlgeformte Aussagen der Zermelo-Fränkel-Mengenlehre. Man kann sich daher die Frage stellen, ob die Peano-Aussagen der Mengenlehre tatsächlich genau dasselbe bedeuten wir die Axiome der Peano-Arithmetik.
Um diese Frage zu beantworten, wollen wir uns überlegen, ob man die Menge \( \mathbb{N} \) auch anders als oben definieren kann, wobei die fünf Peano-Aussagen auch für diese andere Menge (nennen wir sie \( \mathbb{N}' \)) gelten sollen. Dies ist tatsächlich leicht möglich. So hätten wir beispielsweise mit \( 0' := \{ \varnothing \} \), beginnen können. Dann wäre \begin{align} 1' &= (0')^* = 0' \cup \{0'\} = \\ &= \{ \varnothing , \{ \varnothing \}\} = \{ \varnothing, 0' \} \\ 2' &= (1')^* = 1' \cup \{1'\} = \\ &= \{ \varnothing , \{ \varnothing \}, \{ \varnothing , \{ \varnothing \}\} \} = \{ \varnothing, 0', 1' \} \\ & ... \end{align}
Im Vergleich zu unserer vorherigen Definition (dem von Neumannschen Modell) hat sich alles um eine Zahl verschoben: die neue Menge \(0'\) sieht aus wie die alte Menge \(1\) usw.. Auch die so definierte Menge \(N'\) erfüllt die Peano-Aussagen.
Die neue Menge \( 0' := \{ \varnothing \} \) kann man aus der alten Menge \( 0 = \varnothing \) einfach durch die Nachfolger-Abbildung \( 0' = 0 \cup \{ 0 \} = 0^* \) erhalten. Allgemein ist hier \( n' = n^* \), d.h. man kann die gesamte neue Mengendarstellung der natürlichen Zahlen aus der alten Mengendarstellung über die Nachfolger-Abbildung \( ()^* \) erhalten.
Die Frage ist nun, ob man generell jede beliebige Mengendarstellung \(n'\) (nicht unbedingt nur die obige) der natürlichen Zahlen aus dem von Neumannschen Modell durch eine bijektive (d.h. umkehrbar eindeutige) Abbildung (nennen wir sie \(I\)) erhalten kann, so dass \(0' = I(0)\) und \( (n')^* = (I(n))^* = I(n^*) \) ist. Dabei muss die Nachfolger-Abbildung bei der gestrichenen Mengendarstellung nicht unbedingt dieselbe sein wie bei der ursprünglichen ungestrichenen Mengendarstellung. Sie muss nur wieder so gebaut sein, dass die neue Mengendarstellung zusammen mit der neuen Nachfolger-Abbildung die fünf Peano-Aussagen erfüllt. Wenn das alles gegeben ist, so sagt man, die beiden Mengendarstellungen der natürlichen Zahlen sind zueinander isomorph, also gleichwertig und eins-zu-eins ineinander umwandelbar.
Es zeigt sich, dass tatsächlich alle Mengendarstellungen der natürlichen Zahlen in diesem Sinn gleichwertig sind:
Es ist also letztlich egal, durch welche Mengen und durch welche Nachfolger-Funktion wir die natürlichen Zahlen darstellen und die Gültigkeit der fünf Peano-Aussagen sicherstellen. Alle diese Darstellungen (auch Modelle genannt) weisen dieselben strukturellen Eigenschaften auf und lassen sich eins-zu-eins ineinander übersetzen. In der Sprache der Mengenlehre lassen sich die natürlichen Zahlen in diesem Sinn also klar erfassen. Es können nicht unvermutet in irgendeiner Darstellung übernatürliche Zahlen auftreten.
Dies ist anders, wenn wir versuchen, die natürlichen Zahlen im formalen System der Peano-Arithmetik (also ohne den Mengenbegriff) zu erfassen (siehe Kapitel 2.1). Gödels Satz zeigt, dass die Peano-Axiome in diesem System die natürlichen Zahlen nicht unbedingt so festlegen, wie wir dies intuitiv erwarten. In Kapitel 3.1 haben wir gesehen, dass auch Objekte mit den Peano-Axiomen verträglich sind, die wir als übernatürliche Zahlen bezeichnet haben. Im Rahmen der Mengenlehre lässt sich ein explizites Modell für diese übernatürlichen Zahlen angeben (siehe Kapitel 3.1). Solche Modelle sind aber ausgeschlossen, sobald wir die oben angegebene Formulierung der fünf Peano-Aussagen im Rahmen der Mengenlehre verwenden.
Wir sehen also, dass unsere neue Formulierung der fünf Peano-Aussagen im Rahmen der Mengenlehre über die reine Peano-Arithmetik hinausgeht. Die neue Mengen-Formulierung ist nicht gleichwertig zur alten Peano-Arithmetik-Formulierung, sondern sie ist präziser und spiegelt unsere intuitive Vorstellung von natürlichen Zahlen genauer wieder. Dies ist ein Grund dafür, warum man heute die Mengenlehre gegenüber der Peano-Arithmetik als Grundlage der Mathematik bevorzugt. Innerhalb der Mengenlehre lässt sich präziser über natürliche Zahlen sprechen, auch wenn die Mengenlehre zunächst so aussieht, als hätte sie mit natürlichen Zahlen gar nichts zu tun.
Woran liegt es, dass die Mengenlehre übernatürliche Zahlen in der Menge \( \mathbb{N} \) nicht zulässt? Der wichtigste Grund liegt darin, dass die Induktionsaussage \begin{align} & \forall A: \, [ \, (0 \in A) \, \land \, \forall n : \, [(n \in \mathbb{N}) \Rightarrow \\ & \quad \quad \quad ( (n \in A) \Rightarrow ( n^* \in A)) \, ]] \Rightarrow [ \mathbb{N} \subseteq A ] \end{align} für alle Mengen \(A\) gilt und damit alle Eigenschaften erfasst, die die natürlichen Zahlen aufweisen können (was durch ihre Mitgliedschaft in den jeweiligen \(A\)-Mengen angezeigt wird, die diese Eigenschaften repräsentieren). Das können überabzählbar viele Eigenschaften sein! Das Induktionsaxiom der Peano-Arithmetik ohne Mengenlehre erfasst dagegen nur abzählbar viele Aussagen, denn so etwas wie \( \forall A \) ist da nicht erlaubt (denn \(A\) ist dort keine Variable, sondern einer von abzählbar vielen Ausdrücken). Die Bedeutung dieses Unterschieds werden wir uns in Kapitel 4.4 genauer ansehen.
Aufbauend auf den natürlichen Zahlen kann man innerhalb der Mengenlehre nun schrittweise auch Mengendarstellungen für ganze Zahlen, rationale Zahlen und reelle Zahlen finden. Letztlich gelingt es so, die gesamte Standard-Mathematik auf die Zermelo-Fränkel-Axiome der Mengenlehre zurückzuführen.
Da die Zermelo-Fränkel-Mengenlehre die natürlichen Zahlen umfasst (genauer: da sie das Representation-Theorem erfüllt, also jede berechenbare Funktion natürlicher Zahlen darstellen kann, siehe Kapitel 2.4), kann sie nach Gödels Satz nicht zugleich vollständig und widerspruchsfrei sein. Ob sie widerspruchsfrei ist, lässt sich innerhalb der Mengenlehre nicht beweisen.
Nehmen wir an, die Mengenlehre ist widerspruchsfrei (zumindest wurde seit mehr als 75 Jahren noch kein Widerspruch entdeckt). Dann muss die Mengenlehre irgendwo Löcher haben, d.h. es muss Aussagen innerhalb der Mengenlehre geben, die sich aufgrund der Axiome weder beweisen noch wiederlegen lassen.
Nun ist die Mengenlehre andererseits so erfolgreich, dass sie praktisch die gesamte Standardmathematik umfasst. Dort wird man also vermutlich nicht so leicht auf solche Unvollständigkeits-Löcher stoßen. Man könnte daher vermuten, dass diese Löcher eher etwas mit der Existenz oder Nichtexistenz gewisser Mengen zu tun haben, die nicht direkt mit den konstruierbaren mathematischen Objekten in Zusammenhang stehen. Ob es gelingt, Beispiele für solche Löcher zu finden, und was das für die Mathematik bedeutet, wollen wir uns im nächsten Kapitel genauer ansehen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 27 April 2023