Hilberts erstes Problem
Die Kontinuumshypothese ist in ZFC nicht entscheidbar
Konstruierbare Mengen
Determinierte Mengen
Das Axiom der Determiniertheit
Welche Mengenaxiome sind die Besten?
Deskriptive Mengenlehre
Im letzten Kapitel haben wir die Mengenlehre als formales System kennengelernt, so wie sie durch die Zermelo-Fränkel-Axiome (ZFC) festgelegt wird. Wir haben gesehen, dass die Mengenlehre ein Fundament für die gesamte klassische Mathematik bildet. In der Sprache der Mengenlehre lassen sich alle üblichen mathematischen Begriffe wie Zahlen, Relationen, Funktionen usw. konstruieren, d.h. diese Sprache bildet so etwas wie die Maschinensprache der Mathematik, auf die sich alle höheren mathematischen Sprachen zurückführen lassen.
Dennoch wissen wir, dass nach Gödels Satz auch dieses formale System nicht zugleich vollständig und widerspruchsfrei sein kann. Setzen wir Widerspruchsfreiheit voraus, so muss es Aussagen geben, die sich zwar in der formalen Sprache ausdrücken lassen, die sich aber nicht aus den Axiomen ableiten oder widerlegen lassen. Eine solche Aussage wollen wir in diesem Kapitel kennenlernen.
Cantor erfand die Mengenlehre, als er sich mit bestimmten Teilmengen der reellen Zahlen (Punktmengen) beschäftigte – wir sind in Kapitel 4.1 bereits darauf eingegangen und wollen hier kurz die wesentlichen Punkte wiederholen.
Bei seinen Untersuchungen stieß Cantor auf die Frage: "Sind alle unendlichen Mengen von gleicher Mächtigkeit, oder gibt es verschiedene Mächtigkeiten unter den unendlichen Mengen?" Dabei sind zwei Mengen gleich mächtig, wenn sich jedes Element der einen Menge eindeutig einem Element der anderen Menge zuordnen lässt, ohne dass in einer der beiden Mengen Elemente übrig bleiben.
Cantor fand heraus, dass in diesem Sinn die Menge der natürlichen Zahlen und die Menge der Brüche (rationale Zahlen) gleich mächtig sind, denn die Brüche lassen sich in einer geordneten unendlich langen Liste komplett erfassen und durchnummerieren. Die reellen Zahlen sind dagegen mächtiger als die natürlichen Zahlen, denn man kann die reellen Zahlen nicht vollständig durchnummerieren – sie sind überabzählbar. Der Beweis kann mit Hilfe von Cantors Diagonalmethode geführt werden (siehe Kapitel 4.1).
Es ist nun naheliegend, die folgende Frage zu stellen: "Gibt es eine Menge, die in ihrer Mächtigkeit zwischen den natürlichen Zahlen und den reellen Zahlen (die man auch als Kontinuum bezeichnet) liegt?" Gibt es also eine Menge, die sich nicht komplett durchnummerieren lässt, die sich aber auch nicht eins-zu-eins den reellen Zahlen zuordnen lässt, ohne dass reelle Zahlen übrig bleiben?
Da es Cantor nicht gelang, eine solche Menge zu konstruieren, formulierte er im Jahr 1878 seine berühmte Kontinuumshypothese:
Allerdings gelang es Cantor nicht, diese Hypothese zu beweisen, und auch andere Mathematiker hatten nicht mehr Erfolg.
David Hilbert hielt das Problem der Kontinuumshypothese für so bedeutend, dass er es in seinem berühmten Vortrag auf dem internationalen Mathematiker-Kongress zu Paris im Jahr 1900 an erster Stelle nannte:
Überblicken wir die Prinzipien der Analysis und der Geometrie. Die anregendsten und bedeutendsten Ereignisse des letzten Jahrhunderts sind auf diesem Gebiete, wie mir scheint, die arithmetische Erfassung des Begriffs des Kontinuums in den Arbeiten von Cauchy, Bolzano, Cantor und die Entdeckung der Nicht- Euklidischen Geometrie durch Gauss, Bolyai, Lobatschefskiy. Ich lenke daher zunächst Ihre Aufmerksamkeit auf einige diesen Gebieten angehörenden Probleme.
1. Cantors Problem von der Mächtigkeit des Kontinuums Zwei Systeme, d.h. zwei Mengen von gewöhnlichen reellen Zahlen (oder Punkten) heißen nach Cantor äquivalent oder von gleicher Mächtigkeit, wenn sie zu einander in eine derartige Beziehung gebracht werden können, dass einer jeden Zahl der einen Menge eine und nur eine bestimmte Zahl der anderen Menge entspricht. Die Untersuchungen von Cantor über solche Punktmengen machen einen Satz sehr wahrscheinlich, dessen Beweis jedoch trotz eifrigster Bemühungen bisher noch Niemanden gelungen ist; dieser Satz lautet:
Jedes System von unendlich vielen reellen Zahlen d. h. jede unendliche Zahlen- (oder Punkt)menge ist entweder der Menge der ganzen natürlichen Zahlen 1, 2, 3, ... oder der Menge sämmtlicher reellen Zahlen und mithin dem Kontinuum, d.h. etwa den Punkten einer Strecke äquivalent; im Sinne der Äquivalenz gibt es hiernach nur zwei Zahlenmengen, die abzählbare Menge und das Kontinuum.
Aus diesem Satz würde zugleich folgen, dass das Kontinuum die nächste Mächtigkeit über die Mächtigkeit der abzählbaren Mengen hinaus bildet; der Beweis dieses Satzes würde mithin eine neue Brücke schlagen zwischen der abzählbaren Menge und dem Kontinuum.
Es sei noch eine andere sehr merkwürdige Behauptung Cantors erwähnt, die mit dem genannten Satze in engstem Zusammenhange steht und die vielleicht den Schlüssel zum Beweise dieses Satzes liefert. Irgend ein System von reellen Zahlen heißt geordnet, wenn von irgend zwei Zahlen des Systems festgesetzt ist, welches die frühere und welches die spätere sein soll, und dabei diese Festsetzung eine derartige ist, dass, wenn eine Zahl \(a\) früher als die Zahl \(b\) und \(b\) früher als \(c\) ist, so auch stets \(a\) früher als \(c\) erscheint. Die natürliche Anordnung der Zahlen eines Systems heiße diejenige, bei der die kleinere als die frühere, die größere als die spätere festgesetzt wird. Es gibt aber, wie leicht zu sehen ist, noch unendlich viele andere Arten, wie man die Zahlen eines Systems ordnen kann.
Wenn wir eine bestimmte Ordnung der Zahlen ins Auge fassen und aus denselben irgend ein besonderes System dieser Zahlen, ein sogenanntes Teilsystem oder eine Teilmenge, herausgreifen, so erscheint diese Teilmenge ebenfalls geordnet. Cantor betrachtet nun eine besondere Art von geordneten Mengen, die er als wohlgeordnete Mengen bezeichnet und die dadurch charakterisiert sind, dass nicht nur in der Menge selbst, sondern auch in jeder Teilmenge eine früheste Zahl existiert. Das System der ganzen Zahlen 1, 2, 3, ... in dieser seiner natürlichen Ordnung ist offenbar eine wohlgeordnete Menge. Dagegen ist das System aller reellen Zahlen, d. h. das Kontinuum in seiner natürlichen Ordnung offenbar nicht wohlgeordnet. Denn, wenn wir als Teilmenge die Punkte einer endlichen Strecke mit Ausnahme des Anfangspunktes der Strecke ins Auge fassen, so besitzt diese Teilmenge jedenfalls kein frühestes Element. Es erhebt sich nun die Frage, ob sich die Gesamtheit aller Zahlen nicht in anderer Weise so ordnen lässt, dass jede Teilmenge ein frühestes Element, hat, d.h. ob das Kontinuum auch als wohlgeordnete Menge aufgefasst werden kann, was Cantor bejahen zu müssen glaubt. Es erscheint mir höchst wünschenswert, einen direkten Beweis dieser merkwürdigen Behauptung von Cantor zu gewinnen, etwa durch wirkliche Angabe einer solchen Ordnung der Zahlen, bei welcher in jedem Teilsystem eine früheste Zahl aufgewiesen werden kann.
Hilbert spricht in seinem Vortrag zwei Probleme zugleich an: den Beweis der Kontinuumshypothese und den Beweis, dass nach Cantor jede Menge wohlgeordnet werden kann, also jede Teilmenge ein erstes (oder frühestes) Element besitzt. Aus Kapitel 4.2 wissen wir, dass die Aussage, jede Menge könne wohlgeordnet werden, gleichwertig ist zum Auswahlaxiom. Akzeptiert man das Auswahlaxiom in den Zermelo-Fränkel-Axiomen, so kann man den Satz von der Wohlordnung jeder Menge beweisen und umgekehrt. Allerdings sind weder das Auswahlaxiom noch der Wohlordnungssatz konstruktiv. Beide behaupten nur, dass etwas geht bzw. existiert, sagen aber nicht, wie man vorgehen kann. So konnte bis heute keine Wohlordnung auf den reellen Zahlen konstruiert werden. Wir sprachen daher in Kapitel 4.2 vom schwachen Existenzbegriff: Das Zeichen \( \exists \) bedeutet nicht unbedingt "man kann konstruieren", sondern behauptet nur abstrakt, dass etwas existiert und dass diese Existenz nicht zu einem Widerspruch führt. Hilberts Hoffnung, einen direkten Beweis dieser merkwürdigen Behauptung von Cantor zu gewinnen, etwa durch wirkliche Angabe einer solchen Ordnung der Zahlen, bei welcher in jedem Teilsystem eine früheste Zahl aufgewiesen werden kann, konnte bis heute also nicht durchgeführt werden.
Wie sieht es nun mit der Kontinuumshypothese aus? Kann auch sie, so wie der Wohlordnungssatz, aus den Zermelo-Fränkel-Axiomen bewiesen (oder wiederlegt) werden?
Gödel zeigte im Jahr 1940, dass sich die Kontinuumshypothese aufgrund der Zermelo-Fränkel-Axiome (ZFC) nicht widerlegen lässt, und Paul Cohen zeigte im Jahr 1963 schließlich, dass diese Axiome auch nicht stark genug sind, um die Gültigkeit der Kontinuumshypothese zu beweisen. Wir haben hier also ein wunderbares Beispiel für die Auswirkungen von Gödels Satz vor uns: die Kontinuumshypothese ist in der Zermelo-Fränkel-Mengenlehre (ZFC) unentscheidbar. Es ist also keineswegs so, dass nur sehr exotische Aussagen unentscheidbar sind. Sogar Hilberts erstes Problem ist unentscheidbar!
Auf den ersten Blick erscheint es merkwürdig, dass eine so einfache Aussage über Mengen unentscheidbar sein soll. Eigentlich erwartet man, dass die Kontinuumshypothese entweder wahr oder falsch sein sollte. Die Ursache für die Unentscheidbarkeit liegt darin, dass alles, was wir über Mengen wissen, aus den Zermelo-Fränkel-Axiomen hervorgehen muss. Und in diesen Axiomen steht einfach nicht genug Information über Mengen drin, um die Hypothese zu entscheiden.
Man kann nun die Zermelo-Fränkel-Axiome auf zwei Arten erweitern: Man kann die Kontinuumshypothese als neues Axiom mit hinzunehmen, oder man kann ihr Gegenteil als Axiom hinzunehmen. In beiden Fällen erhält man ein Axiomensystem, in dem der Begriff der Menge auf verschiedene Weise weiter präzisiert wird. Doch welche dieser beiden Möglichkeiten würden wir anschaulich als die "richtige" akzeptieren, also als diejenige, die unserem intuitiven Mengenbegriff am ehesten entspricht?
Es ist schwierig, intuitiv zu sagen, ob die Kontinuumshypothese wahr oder falsch sein soll. Der Mengenbegriff ist eben wegen der Möglichkeit unendlicher Mengen nicht mehr hinreichend anschaulich für uns, um über Wahrheit oder Falschheit gleichsam aus dem Bauch heraus zu entscheiden. Unser menschlicher Verstand ist also keineswegs dem formalen System immer überlegen, wenn es um solche Fragen im Umfeld von Gödels Unvollständigkeitssatz geht. Zudem hat die Kontinuumshypothese keinerlei Einfluss auf die Konstruktion und die Eigenschaften der natürlichen Zahlen in der Mengenlehre.
Hilbert und Cantor waren der Meinung, dass die Kontinuumshypothese "wahrscheinlich richtig" ist. Andere Mathematiker neigen zur entgegengesetzten Meinung. Soll man nun also die Kontinuumshypothese oder ihr Gegenteil als Axiom hinzunehmen?
Die meisten Mathematiker würden keines von beidem tun, denn die Kontinuumshypothese (oder ihr Gegenteil) wäre ein ziemlich schwaches Axiom mit wenig interessanten Konsequenzen. Stattdessen versucht man lieber, andere Axiome mit reicheren Konsequenzen zu finden, diese den Zermelo-Fränkel-Axiomen hinzuzufügen und dann zu untersuchen, ob sich die Kontinuumshypothese beweisen oder widerlegen lässt.
Eine Möglichkeit für ein zusätzliches starkes Axiom ist die folgende:
Cantor hatte viele Jahre hindurch versucht, eine Teilmenge der reellen Zahlen zu konstruieren, die mächtiger als die natürlichen Zahlen, aber nicht so mächtig wie die Menge aller reellen Zahlen ist. Es gelang ihm nicht. Man könnte daher versuchen, den Begriff der konstruierbaren Menge zu definieren und dann zu zeigen, dass die Kontinuumshypothese für konstruierbare Mengen richtig ist (d.h. es gibt keine konstruierbare Menge, die in ihrer Mächtigkeit zwischen den natürlichen und den reellen Zahlen liegt).
Gödel war es, der den Begriff der konstruierbaren Mengen präzise formulierte. Dazu legte er acht Mengenoperationen fest, mit denen sich Mengen (ausgehend von der leeren Menge) konstruieren lassen, u.a. die Paarmengenbildung, die Differenzbildung, die Produktmenge, der Wertebereich und andere mehr. Alle Mengen, die sich durch diese Operationen bilden lassen, nennen wir konstruierbare Mengen.
Wie Gödel bewies, kann man den Zermelo-Fränkel-Axiomen die Konstruierbarkeit aller Mengen als weiteres Axiom hinzufügen, ohne dass neue Widersprüche dadurch entstehen:
Dieses Axiom müsste man natürlich in der formalen Sprache der Mengenlehre ausdrücken, was einen sehr langen Ausdruck zur Folge hat. Das ist ein Grund, weshalb manche Mathematiker dieses Axiom nicht mögen.
Man kann sich die Frage stellen, ob Gödel in seinen acht Mengenoperationen wirklich alles Wesentliche bedacht hat, was man zum Konstruieren von Mengen benötigt. Es zeigt sich, dass das tatsächlich so ist, denn man kann beweisen, dass die Gesamtheit aller Gödel-konstruierbaren Mengen die kleinste Gesamtheit bildet, für die alle Zermelo-Fränkel-Axiome gelten. Die Gödel-Operationen bilden also den absolut notwendigen Werkzeugkasten (gleichsam die Grundausstattung) zur Konstruktion von Mengen im Sinne der Zermelo-Fränkel-Mengenaxiome, ohne den man nicht auskommen kann.
Was für Folgen hat es nun, wenn man das Konstruierbarkeitsaxiom zu den Zermelo-Fränkel-Axiomen hinzunimmt? Es zeigt sich, dass dann sowohl das Auswahlaxiom als auch die Kontinuumshypothese bewiesen werden können! Wir sehen also, dass das Konstruierbarkeitsaxiom ein Axiom mit reichen Konsequenzen ist. Es macht das Auswahlaxiom als Axiom überflüssig, denn das Auswahlaxiom entspricht nun einem beweisbaren Satz.
Wenn man nur konstruierbare Mengen im Sinne Gödels zulässt, dann kann man aus jeder konstruierbaren Menge ein Element auswählen, und es gibt keine konstruierbare Menge, die in ihrer Mächtigkeit zwischen den natürlichen Zahlen und den reellen Zahlen liegt. Kein Wunder also, dass Cantor eine solche Menge nicht konstruieren konnte!
Schauen wir uns eine andere Möglichkeit für ein neues Axiom an. Dazu betrachten wir die Zermelo-Fränkel-Axiome ohne das Auswahlaxiom. An die Stelle des Auswahlaxioms setzen wir das Axiom der Determiniertheit, so wie wir oben das Konstruierbarkeitsaxiom an Stelle des Auswahlaxioms verwendet haben (wobei das Auswahlaxiom dadurch zu einer beweisbaren Aussage wurde).
Um das Axiom verstehen zu können, müssen wir zunächst den Begriff der Determiniertheit für Mengen definieren (siehe z.B. Jean-Paul Delahaye: Unendliche Spiele und große Mengen, Spektrum der Wissenschaft 12 / 1998, Seite 46). Dazu geben wir uns irgendeine Menge \(x\) mit reellen Zahlen darin vor. Die rellen Zahlen dieser Menge wollen wir uns als Binärstrings dargestellt vorstellen, z.B. \( 0,1101 ... \) (d.h. \( \frac{1}{2} + \frac{1}{4} + \frac{1}{16} + ... \) ). Nun geben wir zwei Spielern (nennen wir sie \(A\) und \(B\)) die Aufgabe, abwechselnd Nullen oder Einsen zu nennen, wobei unendlich lang gespielt wird. Diese Nullen und Einsen schreiben wir der Reihe nach auf und bilden so einen unendlich langen Binärstring. Dabei darf auch insgesamt einmal ein Komma statt einer Eins oder Null genannt werden. Im Lauf des Spiels entsteht so die Binärdarstellung einer reellen Zahl.
Spieler \(A\) hat nun die Aufgabe, seine Nullen oder Einsen möglichst so zu nennen, dass die entstehende Zahl ein Element der vorgegebenen Menge \(x\) ist. Spieler \(B\) dagegen versucht, seine Nullen und Einsen so zu wählen, dass die Zahl kein Element von \(x\) ist.
Schauen wir uns als erstes Beispiel die Menge \(x = \{ 0, 1, \frac{1}{2} , \frac{1}{4} , \frac{1}{8} , ... \} \) an. In der Binärdarstellung lautet diese Menge \(x = \{ 0 \, ; 1 \, ; 0,1 \, ; 0,01 \, ; 0,001 \, ; ... \} \), d.h. jede Zahl dieser Menge besitzt in der Binärdarstellung höchstens eine Eins an irgendeiner Stelle (und danach nur noch Nullen, die wir aber nicht mehr explizit hinschreiben). Bei dieser Menge hat Spieler \(A\) keine Chance, denn Spieler \(B\) muss einfach nur immer abwechselnd eine Null und eine Eins nennen. Es entsteht eine Zahl der Form \( *1*0*1*0*1*0 ... \) mit einem Komma irgendwo. Dabei steht \(*\) immer für irgendeine von Spieler \(A\) gewählte Zahl (also Null oder Eins). Auf diese Weise erreicht Spieler \(B\), dass mehr als eine Eins im Binärstring vorkommt, so dass die entstehende Zahl nicht in \(x\) enthalten sein kann. Für diese Menge \(x\) gibt es also eine Gewinnstrategie für Spieler B, die garantiert immer funktioniert, egal was Spieler \(A\) macht. Das Spiel ist sogar bereits nach wenigen Zügen entschieden (sobald nämlich die zweite Eins auftaucht).
Als zweites Beispiel betrachten wir die Menge aller reellen Zahlen zwischen \( \frac{1}{8} \) und \( \frac{7}{8} \) (inklusive dieser beiden Grenzen). In Binärdarstellung sind diese Grenzen gleich \(0,001\) und \(0,111\) . Um die Diskussion zu vereinfachen, wollen wir als Startstring "\( 0, \)" (also eine Null vor dem Komma und dann das Komma) vorgeben, wonach Spieler \(A\) am Zug ist. Spieler \(A\) kann nun immer so gewinnen: Als erstes nennt er eine Eins, als zweites eine Null (alles danach ist egal). Die entstehenden Zahlen sind dann von der Form \( 0,1*0 * ... \) . Diese Zahlen sind auf jeden Fall größer als \( \frac{1}{2} \) (wegen der Eins hinter dem Komma) und damit größer als \( \frac{1}{8} \). Andererseits sind diese Zahlen auch kleiner als \( 0,111 \widehat{=} \frac{7}{8} \) (wegen der Null an der dritten Stelle). In diesem Fall besitzt also Spieler \(A\) eine Gewinnstrategie und kann erzwingen, dass die im Wechselspiel entstehende Zahl immer in der Menge enthalten ist.
Als letztes Beispiel wollen wir eine beliebige abzählbare Teilmenge der reellen Zahlen betrachten, z.B. die rationalen Zahlen. Es gibt also eine (unendliche) Liste, in der wir alle diese Zahlen in ihrer Binärdarstellung aufführen können. Spieler \(B\) macht nun folgendes: Wenn er zum ersten mal am Zug ist (d.h. es geht um die zweite Binärstelle), schaut er sich die zweite Binärstelle der ersten Zahl in der Liste an und wählt seine Antwort genau entgegengesetzt zu dieser Stelle. Damit erreicht er, dass die im Spiel entstehende Zahl nicht gleich der ersten Zahl sein kann. Ist er zum zweiten mal am Zug (es geht also um die vierte Binärstelle), wählt er seine Antwort entgegengesetzt zur vierten Binärstelle der zweiten Zahl aus der Liste und so fort. Das Spiel geht nun unendlich lange so weiter, und Spieler \(B\) sorgt damit dafür, dass keine Zahl aus der Liste entstehen kann: nicht die erste, nicht die zweite usw.. Spieler \(B\) besitzt also eine Gewinnstrategie, die analog zu Cantors Diagonalverfahren funktioniert.
Man sagt nun folgendes:
Eine Teilmenge \(x\) reeller Zahlen ist also determiniert, wenn entweder Spieler \(A\) immer dafür sorgen kann, dass der im Spiel entstehende Binärstring eine Zahl aus der Menge ergibt, oder wenn Spieler \(B\) das immer verhindern kann.
Gerne kann man sich Spieler \(A\) als ein Computerprogramm vorstellen, und Spieler \(B\) als einen (beliebig bösartigen) Anwender. Der Binärstring stellt dann eine unendliche Kette von abwechselnden Anwenderaktionen und Computerreaktionen dar, also eine unendliche Interaktionskette zwischen Computerprogramm und Anwender. Stürzt das Programm ab, hat der Anwender gewonnen, andernfalls der Computer. Wünschenswert ist also eine Gewinnstrategie für den Computer, d.h. ein absolut narrensicheres Computerprogramm, das nie abstürzt.
Wir haben oben gesehen, dass jede abzählbare Menge (die also gleich-mächtig wie die natürlichen Zahlen ist) determiniert ist. Auch für einige überabzählbare Teilmengen der reellen Zahlen haben wir die Determiniertheit oben gesehen. Es stellt sich daher die Frage, wie weit man innerhalb der Zermelo-Fränkel-Mengenlehre (mit Auswahlaxiom) gehen kann.
Im Jahr 1953 gelang es David Gale und Frank M. Steward, zu beweisen, dass
jede offene Teilmenge der reellen Zahlen
determiniert ist (eine Menge reller Zahlen ist offen, wenn die Menge
keinen Rand hat und jeder Punkt der Menge ein innerer Punkt ist;
z.B. ist die Menge aller reellen Zahlen zwischen 0 und 1 (ohne 0 und 1 selbst)
offen). Dieses Ergebnis konnte im Jahr 1975 durch
Donald Martin auf alle Borelschen Mengen erweitert werden.
Zu den Borelschen Mengen gehören neben den offenen und abgeschlossenen
Mengen auch komplizierte fraktale Mengen
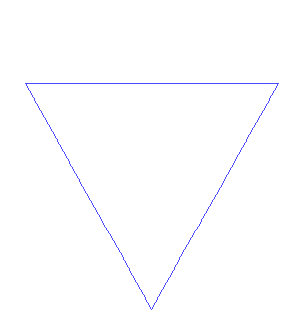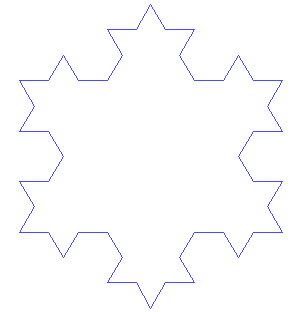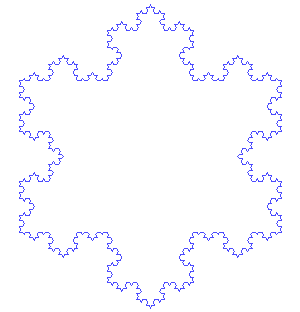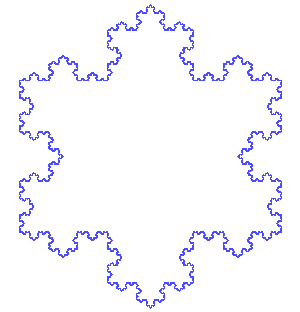
wie die Kochsche Schneeflockenkurve, die weder offen noch abgeschlossen
sein müssen. Borelschen Mengen lässt sich immer ein Volumen (allgemeiner: ein Maß) zuordnen.
Die Kontinuumshypothese ist für alle Borelschen Mengen beweisbar.

Der nächste Schritt wäre, die Determiniertheit für alle projektiven Mengen zu beweisen (dazu gehören Mengen, die noch komplexer sein können als Borelsche Mengen). Dies gelang nicht, und es konnte schließlich gezeigt werden, dass ein solcher Beweis einen Widerspruch zum Auswahlaxiom erzeugen würde. Das Auswahlaxiom hat die Existenz gewisser nicht-determinierter Mengen zur Folge.
Nun könnte man aber auf die Idee kommen, das Auswahlaxiom zu streichen und es durch folgendes Axiom zu ersetzen:
Da dieses Axiom dem Auswahlaxiom (und damit auch dem Konstruierbarkeitsaxiom) widerspricht, muss man das Auswahlaxiom in dieser Variante der Mengenlehre weglassen. Ob allerdings das Axiom der Determiniertheit konsistent zu den Zermelo-Fränkel-Axiomen ist, wurde meines Wissens noch nicht endgültig geklärt. Es gibt allerdings viele Gründe, die für diese Konsistenz sprechen.
Man könnte nun annehmen, dass man ohne das nun fehlende Auswahlaxiom nicht mehr alle notwendigen mathematischen Objekte konstruieren kann. Aber es gibt eine schwächere Version des Auswahlaxioms, die sich mit Hilfe des Axioms der Determiniertheit beweisen lässt: Man kann zwar nicht mehr aus allen Mengen eines beliebigen Mengensystems pro Menge je ein Element auswählen, aber man kann immer noch aus jeder abzählbaren (also durchnummerierbaren) Sammlung von nicht-leeren Teilmengen der reellen Zahlen je eine reelle Zahl auswählen (countable axiom of choice).
Die Zermelo-Fränkel-Mengenlehre mit dem Axiom der Determiniertheit hat noch eine andere schöne Eigenschaft: jede Teilmenge der reellen Zahlen ist Lebesgue-messbar, d.h. man kann jeder Teilmenge eine Länge (bzw. in mehr Dimensionen eine Fläche, Volumen etc.) zuordnen. Das Auswahlaxiom hingegen ermöglicht auch die Konstruktion nicht-messbarer Teilmengen der reellen Zahlen, was zu merkwürdigen Konsequenzen führt. So kann man beim sogenannten Kugelparadoxon mit Hilfe des Auswahlaxioms beweisen, dass man eine massive Kugel so in endlich viele Teile zerlegen kann, dass man aus diesen Teilen allein durch Drehen und Verschieben der Teile zwei neue massive Kugeln zusammensetzen kann, die jeweils genau so groß sind wie die Ausgangskugel (Banach-Tarski-Paradox, siehe z.B. Spektrum der Wissenschaft, April 1990, Seite 12). Die Teile, in die man die Kugel zerlegt, sind dabei nicht-messbare Mengen, d.h. man kann sich das Zerlegen der Kugel nicht als ein physisches Zersägen vorstellen, sondern die Kugel wird in endlich viele vollkommen wirre Punktemengen zerlegt. Diese Mengen werden nicht explizit angegeben, sondern es wird nur bewiesen, dass es solche Mengen gibt (hier kommt wieder der nicht-konstruktive Charakter des Auswahlaxioms zum Ausdruck).
Das Axiom der Determiniertheit ermöglicht es, die Kontinuumshypothese zu beweisen. Es gibt also in dieser Version der Mengenlehre (wie schon zuvor beim Konstruierbarkeitsaxiom) keine Menge, die in ihrer Mächtigkeit zwischen den natürlichen Zahlen und dem Kontinuum (den reellen Zahlen) liegt. Insofern ist das Axiom der Determiniertheit (wie schon zuvor das Konstruierbarkeitsaxiom) mächtiger (oder vielleicht sollte man genauer sagen: einschränkender) als das Auswahlaxiom.
Es lässt sich mit dem Axiom der Determiniertheit sogar beweisen, dass die reellen Zahlen nicht wohlgeordnet werden können, weil jede wohlgeordnete Teilmenge der reellen Zahlen entweder endlich oder abzählbar sein muss. Nicht jede Menge mit reellen Zahlen muss also ein kleinstes (oder besser erstes oder frühestes) Element im Sinne einer Ordnungsrelation haben. Dies entspricht unserer Anschauung über die reellen Zahlen. Das Auswahlaxiom und damit auch das Konstruierbarkeitsaxiom führen hier zu einem anderen Ergebnis, denn in diesen Varianten der Mengenlehre lässt sich jede Menge wohlordnen.
Welche ist nun die beste Variante der Mengenlehre? Zur Auswahl stehen u.a. die Zermelo-Fränkel-Axiome inclusive Auswahlaxiom (dann ist die Kontinuumshypothese nicht entscheidbar, und jede Menge kann wohlgeordnet werden), die Ersetzung des Auswahlaxioms durch das Konstruierbarkeitsaxiom (dann ist das Auswahlaxiom beweisbar, die Kontinuumshypothese ist beweisbar und jede Menge kann wohlgeordnet werden) oder die Ersetzung des Auswahlaxioms durch das Axiom der Determiniertheit (dann gilt statt dem Auswahlaxiom das abzählbare Auswahlaxiom (countable axiom of choice), die Kontinuumshypothese ist beweisbar und nicht jede Menge kann wohlgeordnet werden). Jede dieser Varianten präzisiert den Mengenbegriff auf verschiedene Weise mit der Folge, dass die so beschriebenen Mengen unterschiedliche Eigenschaften aufweisen. Welche Version man bevorzugt, hängt letztlich davon ab, was man mit dem entsprechenden formalen System anfangen will. Für Untersuchungen im Rahmen der Spieltheorie eignet sich beispielsweise besonders das Axiom der Determiniertheit. In anderen Zusammenhängen mag eine andere Variante nützlicher sein. Eine objektive Wahrheit, welches denn nun die richtigen Axiome für die Mengenlehre und damit für die Mathematik sind, gibt es nicht!
Man könnte nun den Verdacht haben, dass sich auch die übrigen Zermelo-Fränkel-Axiome gegen andere Axiome austauschen lassen könnten, so dass man auf diese Weise weitere Varianten der Mengenlehre erzeugen kann. Vielleicht kann man sogar neue Versionen des uneingeschränkten Komprehensions-Axiomenschemas \[ \exists x: \forall y : \, [ (y \in x) \Leftrightarrow F(y) ] \] (mit neuen Möglichkeiten für die Aussage \(F(y)\) ) finden, die man als neue Axiome hinzufügen kann, so dass sich weitere Mengen konstruieren lassen?
Es gibt eine interessante alternative Möglichkeit aus dem Jahr 1956, die Mengenlehre über Axiome zu definieren: Ackermanns Mengenlehre (siehe Karlis Podnieks: What is Mathematics: Gödel's Theorem and Around, Kap. 2.4: Around the Continuum Problem). Es konnte gezeigt werden, dass Ackermanns Mengenlehre und die Zermelo-Fränkel-Mengenlehre ohne Auswahlaxiom gleichwertig bezüglich ihrer Aussagen über Mengen sind. Dies zeigt, dass die Zermelo-Fränkel-Axiome nicht einfach zufällig gewählt wurden, sondern dass sie den harten Kern der Mengenlehre bilden. Genau diese Axiome scheint man zu brauchen, wenn man alle für die Mathematik notwendigen Mengen konstruieren möchte. Neue Versionen des Komprehensions-Axioms, die die Konstruktion neuer Mengen ermöglichen, sind daher nicht zu erwarten. Weitere Axiome werden sich wohl nicht mit der Konstruktion von neuen Mengen befassen, sondern Eigenschaften von Mengen spezifizieren oder allgemeine, nicht-konstruktive \( \exists \) -Aussagen machen. Der konstruktive Teil der Mathematik (also z.B. der Aufbau der verschiedenen Zahlen) wird von solchen Axiomen kaum berührt werden. Man kann daher sagen, dass sich zumindest ein Teil von Hilberts Vision erfüllen lässt: der konstruktive Teil der Mathematik lässt sich in einem formalen System erfassen. Die Zermelo-Fränkel-Axiome der Mengenlehre sind ein guter Kandidat für ein solches formales System.
Ein interessanter Weg, der heute häufig beschritten wird, ist die deskriptive Mengenlehre (siehe z.B. Podnieks: Appendix 4: Descriptive Set Theory). Anstatt verschiedene Alternativen zum Auswahlaxiom auszuprobieren, behält man das Auswahlaxiom (und natürlich die übrigen Zermelo-Fränkel-Axiome) bei. Das Auswahlaxiom ermöglicht die Existenz weit komplizierterer Mengen als z.B. das Konstruierbarkeitsaxiom (das nur konstruierbare Mengen erlaubt) oder als das Axiom der Determiniertheit (das nur determinierte Mengen zulässt). Deshalb kann auch die Kontinuumshypothese nicht bewiesen werden, denn das Auswahlaxiom ist so allgemein, dass sich die Existenz sehr komplizierter Mengen mit einer Mächtigkeit zwischen den natürlichen und den reellen Zahlen nicht ausschließen (allerdings aber auch nicht beweisen) lässt. Man verwirft die Möglichkeit solcher Mengen nun nicht einfach durch ein passendes Axiom, sondern man versucht, sich schrittweise von einfachen zu komplexeren Mengen vorzuarbeiten und dabei herauszufinden, für welche Mengen sich die Kontinuumshypothese oder die Determiniertheit (oder die Konstruierbarkeit) noch beweisen lässt.
Hier sind einige Fragen, die man auf diese Weise untersuchen kann:
Diese Vorgehensweise haben wir oben bei den determinierten Mengen bereits kennengelernt. Wir haben uns schrittweise von einfachen zu komplexen Mengen vorangetastet und dabei
darauf untersucht, ob die jeweiligen Mengen noch determiniert sind.
Wir sehen, dass die Mengenlehre ein sehr reichhaltiges Forschungsgebiet ist, das ganz unterschiedliche Wege und Vorgehensweisen ermöglicht. Die Komplexität der Mengen, die sich konstruieren lassen, kann enorm werden (man spricht teilweise von mathematischen Monstern), und die Wahl des Auswahlaxioms bzw. seiner Alternativen bestimmt letztlich, welche Komplexität man zulassen will. Ein formales System, das als Fundament für die gesamte Mathematik in Frage kommen will, muss sicher eine solche Reichhaltigkeit aufweisen, so wie auch Turings Maschine in der Lage ist, alles Berechenbare zu berechnen (Church-These, siehe Kapitel 2.3). Vielleicht findet man eines Tages auch eine Church-These für die Mathematik, in der die Mengenlehre oder ein noch reichhaltigeres System die Rolle von Turings Maschine übernimmt? Beim Begriff der Berechenbarkeit hatte man zeigen können, dass viele verschiedene Definitionen dieses Begriffs zur Definition durch die Turingmaschine gleichwertig sind. Analog könnten verschiedene formale Systeme (z.B. verschiedene Versionen der Mengenlehre), die als Fundament der Mathematik in Frage kommen, zueinander gleichwertige Axiome aufweisen (Ackermanns Mengenlehre ist ein solches Beispiel, wie wir oben gesehen haben). Dies wäre sicher eine interessante Variante von Hilberts Vision!
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 12 March 2023