
Vorbemerkung
Der Wortschatz formaler Systeme
Logische Symbole und wohlgeformte Ausdrücke
Axiome der Logik
Logik erster und zweiter Ordnung
Modelle und Interpretationen formaler Systeme
Interpretation und Wahrheit
Manche Aussagen sind immer wahr
Gödels Vollständigkeitssatz der klassischen Logik
Der Modellexistenzsatz
Skolems Paradoxon
Modelle der Peano-Arithmetik
Sich an den Haaren aus dem Sumpf ziehen
Wie kann man etwas definieren?
Anmerkung: Dieses Kapitel orientiert sich u.a. an den Texten von Karlis Podnieks (siehe Literaturangaben am Ende dieses Kapitels)
Bei der Betrachtung formaler System wie der Peano-Arithmetik oder der Zermelo-Fränkel-Mengenlehre sind wir in den bisherigen Kapiteln nicht auf die genaue Form der Logik und damit nicht auf die genaue Form der formalen Sprache eingegangen, in der diese Systeme formuliert werden. Wir haben zwar die Axiome dieser Systeme kennengelernt, haben aber die grammatikalischen Regeln der zugehörigen formalen Sprache in Kapitel 2.1 nur kurz gestreift. Dies wollen wir in diesem Kapitel nachholen.
In Kapitel 2.1 haben wir weiterhin gesehen, dass man erst nach einer Interpretation der formalen Begriffe davon reden kann, dass eine Aussage wahr oder falsch ist. Was wir genau unter einer Interpretation verstehen, wollen wir uns ebenfalls in diesem Kapitel ansehen. Dabei werden wir den Begriff des Modells kennenlernen, den wir an mehreren Stellen bereits ohne genaue Erklärung verwendet haben.
Im Lauf der Diskussion verschiedener Modelle werden wir auf ein sehr interessantes und paradox anmutendes Ergebnis stoßen, das den Namen Skolems Paradoxon trägt. Dieses Paradoxon wirft viele Fragen über die unabhängige Existenz einer mathematischen Welt (z.B. die reellen Zahlen) auf – ähnlich wie die Quantentheorie die unabhängige Existenz einer absoluten physikalischen Wirklichkeit in Frage stellt. Als Physiker hat mich dieses Paradoxon daher besonders interessiert.
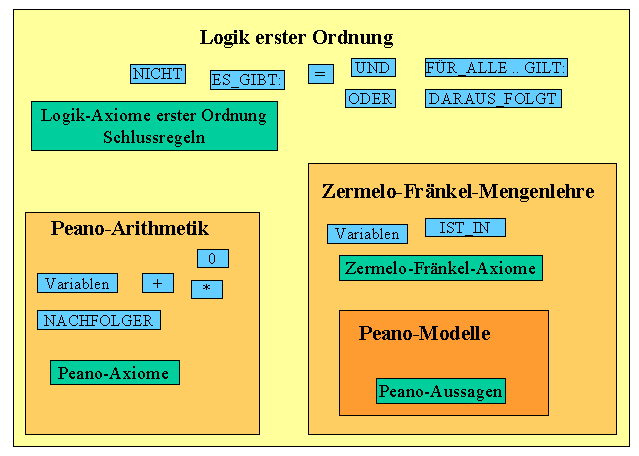
Beginnen wir damit, uns den grammatikalischen Aufbau einer formalen Sprache, so wie sie für die Peano-Arithmetik oder die Mengenlehre benötigt wird, genauer anzusehen. Dabei werden wir uns auf Logik erster Ordnung beschränken, da dies dem heute üblichen Standard entspricht. Auf Logik zweiter Ordnung gehen wir später nur kurz ein.
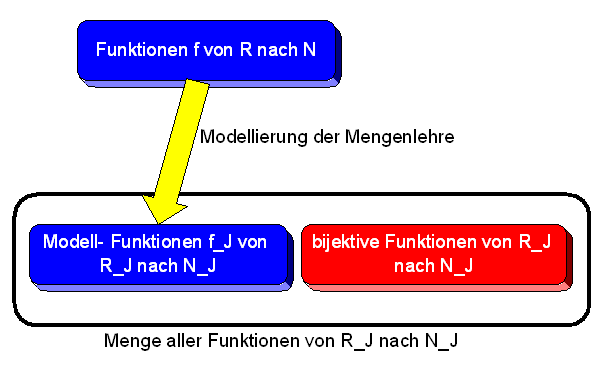
Ein formales System dient dazu, Aussagen über gewisse Objekte zu machen, z.B. Aussagen über Zahlen oder Mengen (wir wollen uns in einem formalen System dabei auf eine Objektsorte beschränken). Die Vorstellung dabei ist, dass diese Objekte aus einer bestimmten Welt, einem Wertebereich oder einer Domäne entstammen. So sollen die Objekte der Peano-Arithmetik natürliche Zahlen sein, die Objekte der Mengenlehre dagegen Mengen. Das formale System soll nun gerade so aufgebaut werden, dass die formalen Objekte sich genauso verhalten, wie wir das von natürlichen Zahlen oder von Mengen erwarten. Wie weit dies gelingt, werden wir noch sehen (wir wissen ja bereits, dass Gödels Satz hier zu Überraschungen führen kann, siehe Kapitel 3.1).
Um beliebige Objekte in Aussagen darzustellen, benötigen wir Variablen (also Platzhalter für beliebige Objekte), die wir mit Buchstaben wie \(x, y, ... \) (bzw. mit abzählbar vielen Buchstabenkombinationen) bezeichnen. Wichtig ist dabei, dass diese Variablen nur für Objekte stehen, nicht aber z.B. für Eigenschaften von Objekten. Genau dies ist das Kennzeichen von Sprachen erster Ordnung (bzw. Logik erster Ordnung).
Manchmal ist es notwendig, einigen Objekten einen besonderen Namen zu geben. Dies tun wir, indem wir bestimmte feststehende Bezeichnungen (Konstanten) in der Sprache erlauben. So gibt es in der Peano-Arithmetik ein Objekt namens \( 0 \), das die natürliche Zahl Null darstellen soll. In der Mengenlehre benötigen wir dagegen überhaupt keine Konstanten (die leere Menge braucht nicht extra benannt zu werden, siehe Kapitel 4.2). Generell darf es abzählbar viele Konstanten geben.
In der Peano-Arithmetik brauchen wir noch Funktionsbezeichner, nämlich \(+\) (Addition) und \( \cdot \) (Multiplikation) sowie die Nachfolger-Funktion \( ()^* \). Die Mengenlehre kommt ohne Funktionsbezeichner aus. Generell darf es nur endlich viele Funktionsbezeichner geben.
Als letzte Zutat benötigen wir sogenannte Prädikatsbezeichner, die bestimmte Eigenschaften oder Relationen (Beziehungen) zwischen den Objekten unserer Domäne darstellen sollen. Fast jedes formale System besitzt einen Prädikatsbezeichner für Gleichheit, also \( = \) . Die Mengenlehre besitzt zusätzlich den Bezeichner \( \in \) für ist Element von. Generell darf es nur endlich viele Prädikatsbezeichner geben.
Damit haben wir den Wortschatz der formalen Sprache festgelegt. Aus diesen Worten können wir nun zunächst sogenannte Terme zusammensetzen, die bestimmte Objekte und Funktionen darstellen. Die einfachsten Terme sind Variablen und Konstanten. Aber auch Strings, die daraus über Funktionen zusammengesetzt werden (z.B. \( x \cdot y \) oder \( x + y \) oder \( x^* \) ), sind Terme. Allgemein gilt: Wenn \(f\) ein Funktionsbezeichner mit \(k\) Argumenten ist, und die Argumente \( t_1 \) bis \( t_k \) sind Terme (z.B. Variablen oder Konstanten), dann ist auch \( f(t_1, ... , t_k)\) ein Term. Andere Terme gibt es nicht. Da die Mengenlehre keine Funktionsbezeichner hat, gibt es dort außer Variablen und Konstanten keine anderen Terme.
Mit Hilfe von Prädikatsbezeichnern lassen sich aus Termen sogenannte elementare Ausdrücke (auch elementare oder atomare Formeln bzw. Aussagen genannt) aufbauen. Wenn \(p\) ein Prädikatsbezeichner mit mit \(k\) Argumenten ist, und die Argumente \( t_1 \) bis \( t_k \) sind Terme, dann ist \( p(t_1, ..., t_k) \) ein elementarer Ausdruck. Andere elementaren Ausdrücke gibt es nicht. In der Peano-Arithmetik sind \( x + 0 = x \) oder \( x \cdot y = y \cdot x \) und in der Mengenlehre sind \( y \in x \) sowie \( x = y \) Beispiele für elementare Ausdrücke.
Um zusammengesetzte Ausdrücke bilden und nach den Regeln der Logik manipulieren zu können, müssen wir den Wortschatz um einige Zeichenketten erweitern. Es ist üblich, die folgenden logischen Verbinder und Quantifizierer einzuführen (wobei es unterschiedliche Schreibweisen gibt; \(B, C\) usw. bezeichnen dabei im Folgenden irgendwelche elementaren Ausdrücke; \(x, y\) usw. bezeichnen Variablen):
|
Die Äquivalenzrelation \( \Leftrightarrow \) kann als Abkürzung definiert werden: \( B \Leftrightarrow C \) steht für \( (B \Rightarrow C) \land (C \Rightarrow B) \). Das exklusive oder (also entweder-oder) entspricht dem Ausdruck \( \neg (B \Leftrightarrow C) \).
Mit Hilfe der logischen Zeichenketten können wir nun allgemein wohlgeformte Ausdrücke definieren: Zu den wohlgeformten Ausdrücken gehören zunächst die oben definierten elementaren Ausdrücke. Ferner lassen sich aus zwei gegebenen wohlgeformten Ausdrücken \(B\) und \(C\) die wohlgeformten Ausdrücke \( B \Rightarrow C \) und \(B \land C\) und auch \(B \lor C\) sowie \(\neg B\) bilden. Nimmt man eine Variable \(x\) hinzu, dann sind auch \( \forall x: \, B \) und \( \exists x: \, B \) wohlgeformte Ausdrücke. Andere wohlgeformte Ausdrücke gibt es nicht.
Um den logischen Symbolen eine Bedeutung zu geben, benötigt man eine Reihe logischer Axiome (d.h. Startzeichenketten) und Ableitungsregeln (siehe z.B. Karlis Podnieks: Introduction to Mathematical Logic,). \(B, C\) und \(D\) stehen im Folgenden für beliebige wohlgeformte Ausdrücke.
|
Zusätzlich zu den logischen Axiomen, die ja als Start-Zeichenketten verwendet werden können, benötigt man noch Regeln, die aus gewissen vorgegebenen Zeichenketten neue Zeichenketten erzeugen können. Solche Regeln nennt man auch syntaktische Umformungsregeln oder Schlussregeln (engl. rules of inference). Sie stellen das logische Schlussfolgern im formalen System dar. In den folgenden Umformungsregeln sind \(B, C\) und \(F\) irgendwelche wohlgeformten Ausdrücke, und \(G\) ist ein wohlgeformter Ausdruck, der nicht die freie Variable \(x\) enthält. Mit \(F(x)\) deuten wir an, dass \(F\) eine freie Variable \(x\) enthält:
|
Damit haben wir alle Axiome und Regeln der klassischen Logik (auch Prädikatenkalkül mit Gleichheit genannt) beisammen.
Nicht alle Axiome der Logik sind unstrittig. So kann man beispielsweise über das Axiom \[ \neg B \Rightarrow (B \Rightarrow C) \] von oben durchaus diskutieren. Dieses Axiom sagt, dass wenn sowohl \(B\) als auch das Gegenteil \( \neg B \) gelten, jede beliebige Aussage \(C\) folgt. Aus einem Widerspruch folgt demnach Beliebiges. Man braucht dieses Axiom beispielsweise für den Beweis der Regel \( \neg\neg B \Rightarrow B \) von der doppelten Verneinung.
Ein anderes Problem-Axiom ist das Axiom des ausgeschlossenen Dritten \[ B \lor \neg B \] Dieses Axiom sagt, dass für jede Aussage \(B\) immer entweder \(B\) oder ihr Gegenteil \( \neg B \) gilt. Man braucht dieses Axiom z.B. für Widerspruchsbeweise. Nach Gödel gibt es aber in hinreichend mächtigen formalen Systemen unentscheidbare Aussagen, d.h. weder \(B\) noch \( \neg B \) sind beweisbar. Lässt man \( B \lor \neg B \) als Axiom weg, so erhält man die sogenannte konstruktive Logik. Lässt man zusätzlich noch das obige Problemaxiom \( \neg B \Rightarrow (B \Rightarrow C) \) weg, so spricht man von der minimalen Logik.
Die konstruktive Logik unterscheidet sich von der klassischen Logik hauptsächlich durch die Interpretation der Oder-Verknüpfung \( \lor \) und durch die Interpretation von Existenzaussagen. Um eine Aussage \( B \lor C \) in der klassischen Logik zu beweisen, genügt es beispielsweise, aus der Aussage \( \neg (B \lor C) \) einen Widerspruch herzuleiten. Dann weiß man allerdings noch immer nicht, ob nun \(B\) oder ob \(C\) beweisbar ist. In der konstruktiven Logik dagegen muss man entweder \(B\) oder \(C\) beweisen, um \( B \lor C \) beweisen zu können.
Analog muss man in der konstruktiven Logik für den Beweis der Existenzaussage \( \exists x : B(x) \) ein bestimmtes \(x\) angeben, für das \(B(x)\) gilt (d.h. \(x\) existiert im Sinn des starken Existenzbegriffs: man kann es angeben!). In der klassischen Logik dagegen kann man zum Beweis von \( \exists x : B(x) \) einfach aus \( \forall x : \neg B(x) \) einen Widerspruch ableiten. Das bedeutet aber nicht, dass man \(x\) angeben kann. Es ist lediglich gezeigt, dass die Annahme, ein passendes \(x\) existiere nicht, zu einem Widerspruch führt, d.h. \(x\) existiert hier im Sinn des schwachen Existenzbegriffs.
Im Folgenden legen wir die Regeln der klassischen Logik zugrunde. Jedes formale System, das auf diesen Regeln aufbaut, wird als System erster Ordnung bezeichnet. Dabei kommen zu den logischen Axiomen noch spezielle weitere Axiome hinzu, die die Beziehungen und Eigenschaften der betrachteten Objekte genauer festlegen. In der Peano-Arithmetik sollen die Peano-Axiome so die Eigenschaften der natürlichen Zahlen festlegen (siehe Kapitel 2.1), und in der Mengenlehre sollen die Zermelo-Fränkel-Axiome festlegen, was wir unter Mengen verstehen (siehe Kapitel 4.2).
Systeme erster Ordnung sind dadurch gekennzeichnet, dass die Quantoren \( \exists \) und \( \forall \) nur auf Variablen wirken können, also auf die Objekte, die durch das formale System beschrieben werden sollen. Sie wirken nicht auf Aussagen über die Objekte (z.B. \( \forall A(x) : ... \) ). Dies kann man gut am Induktionsaxiom der Peano-Arithmetik erkennen: \begin{align} [ A(0) \, & \land \,(\forall n : (A(n) \Rightarrow A(n^*) )] \\ & \Rightarrow \, [ \forall n : (A(n) ] \end{align} Wir haben hier ein Axiomenschema vor uns, das zu jeder wohlgeformten Aussage \(A(n)\) mit einer freien Variablen \(n\) ein Axiom liefert. Da sich diese Aussagen \(A(n)\) mechanisch auflisten lassen (sie sind also rekursiv abzählbar), lassen sich auch die entsprechenden Induktionsaxiome mechanisch auflisten.
Das ändert sich, wenn wir das Induktionsaxiom in einer Sprache zweiter Ordnung formulieren: \begin{align} \forall A : [[ A(0) \, & \land \,(\forall n : (A(n) \Rightarrow A(n^*) )] \\ & \Rightarrow \, [ \forall n : (A(n) ] ] \end{align} Dieses Axiom soll für alle Eigenschaften \(A\) gelten, die man gewissen natürlichen Zahlen zuschreiben kann. Das Problem ist aber, dass man nicht so recht weiß, was alle Eigenschaften bedeuten soll. Man benötigt letztlich ein allgemeineres formales System erster Ordnung als Metatheorie (z.B. die Mengenlehre), um dies festzulegen. Tut man dies, so kann man z.B. wie folgt argumentieren:
Jede Eigenschaft \(A\), die man bestimmten natürlichen Zahlen zuschreiben kann, ist dadurch festgelegt dass man für jede natürliche Zahl \(n\) angeben kann, ob \(n\) die Eigenschaft besitzt oder nicht. Man kann daher jede Eigenschaft \(A\) eindeutig dadurch festlegen, dass man alle natürlichen Zahlen \(n\), die die Eigenschaft \(A\) besitzen, in einer Menge \( M_A = \{ n \in \mathbb{N} ; \, A(n) \} \) versammelt ( \( \mathbb{N} \) war die Menge der natürlichen Zahlen im Standardmodell). Jede Teilmenge der natürlichen Zahlen definiert damit eine Eigenschaft \(A\) und umgekehrt. Dabei darf die Teilmenge \( M_A \) auch gleich \( \mathbb{N} \) sein, denn schließlich gibt es Eigenschaften, die alle natürlichen Zahlen aufweisen. Nun sind die (unendlich großen) Teilmengen der natürlichen Zahlen aber überabzählbar, denn man kann mit Cantors Diagonalelement zu jeder Liste von Teilmengen eine neue Teilmenge konstruieren, die nicht in der Liste enthalten ist. Somit umfasst das Induktionsaxiom in der Sprache zweiter Ordnung überabzählbar viele Eigenschaften, das Induktions-Axiomenschema erster Ordnung dagegen nur abzählbar viele Eigenschaften (nämlich diejenigen, die sich durch Aussagen der Peano-Arithmetik ausdrücken lassen). Welche Konsequenzen das hat, wollen wir uns weiter unten noch genauer ansehen.
Theorien, die in einer Sprache zweiter Ordnung formuliert sind, sodass man über alle Eigenschaften sprechen kann, benötigen zur Konkretisierung im Allgemeinen eine umfassendere Theorie erster Ordnung, in die sie gleichsam eingebettet sind. Man spricht auch von der Interpretation oder von einem Modell der Theorie. Heute vertritt man weitgehend die Meinung, dass alle wirklich funktionierenden grundlegenden mathematischen Theorien in einer Sprache erster Ordnung formuliert werden müssen (oder zumindest ein Modell in einer Metatheorie erster Ordnung haben). Daher wollen wir Sprachen höherer Ordnung hier zunächst ignorieren und erst weiter unten noch einmal darauf zurückkommen.
In einer formalen Theorie erster Ordnung spielen die Begriffe wahr und falsch zunächst keine Rolle. Man kann die Theorie mit einem großen Computerprogramm vergleichen, das Zeichenketten manipuliert und ausgehend von den Start-Zeichenketten (den Axiomen) in der Lage ist, eine vollständige (unendlich lange) Liste aller daraus ableitbaren wohlgeformten Ausdrücke beliebig weit zu erzeugen (siehe Kapitel 2.2).
Um von einer wahren oder falschen Aussage sprechen zu können, muss man den formalen Zeichen der Theorie eine Interpretation geben. Man benötigt ein Modell der formalen Zeichen. Ein solches Modell kann Begriffe der Anschauung verwenden, z.B. Geraden in einer Ebene oder Großkreise auf einer Kugel für die geometrischen Axiome Euklids (siehe Kapitel 2.1). Häufig verwendet man für ein Modell auch intuitiv klare mathematische Konzepte, bei denen man anschaulich beurteilen kann, was wahr und was falsch ist.
Wenn man jedoch auf schwierige Fragen bei der Interpretation eines formalen Systems stößt, bleibt einem in letzter Konsequenz nichts anderes übrig, als sich bei der Interpretation auf die Begriffe eines anderen möglichst umfassenden formalen mathematischen Systems zu stützen. Ein solches System ist die Mengenlehre mit den Zermelo-Fränkel-Axiomen, zusammen mit der klassichen Logik erster Ordnung. Die Zermelo-Fränkel-Mengenlehre soll also als Metatheorie für andere mathematische Theorien (z.B. die Peano-Arithmetik) dienen.
Wir wollen daher eine Interpretation (ein Modell) (abgekürzt J) eines formalen Systems (nennen wir es L) präzise so festlegen:
Definition eines Modells \(J\) zu einem formalen System \(L\):
|
Zum besseren Verständnis dieser Idee schauen wir uns noch einmal die Interpretation der Peano-Arithmetik aus Kapitel 4.2 an: Die Domäne \( D_J \) , die den Wertebereich der Variablen im Modell darstellt, ist gleich der Menge \( \mathbb{N} \), also \( D_J = \mathbb{N} = \{ i_J(0), i_J^*(0), ... \}\) . Die Konstante \(0\) wird im Modell durch die leere Menge \( \varnothing \) dargestellt, also \( i_J(0) = \varnothing \) , und die Nachfolger-Funktion \( ()^* \) wird im Mengen-Modellraum durch die Mengenfunktion \( n \cup \{n\} \) dargestellt. Wir hatten dieses Modell in Kapitel 4.2 als von Neumannsches Modell oder auch als Standardmodell bezeichnet.
Interessant ist die Interpretation von Prädikatsbezeichnern: ihnen wird eine Teilmenge von \( D_J \times ... \times D_J \) zugeordnet (das karthesische Produkt \( A \times B \) zweier Mengen hatten wir in Kapitel 4.2 definiert).
Nehmen wir ein Prädikat \(p(x)\) mit einer freien Variablen \(x\), das die Aussage \(x\) ist eine Primzahl darstellt. Dann wird \(p\) durch die Menge aller Primzahl-Mengen aus \mathbb{N} dargestellt, also \( i_J(p) = \{ 1, 2, 3, 5, 7, ... \} \) . Analog ist es bei Prädikaten mit zwei Argumenten, die eine Beziehung zwischen zwei natürlichen Zahlen ausdrücken (z.B. \(x\) ist kleiner als \(y\) oder \(x\) ist das Doppelte von \(y\)). Solche Prädikate entsprechen (zweiwertigen) Relationen zwischen Elementen der Menge \( \mathbb{N} \), und solche Relationen waren gerade definiert als Teilmengen von \( \mathbb{N} \times \mathbb{N} \) (siehe Kapitel 4.2). Wir sehen also, dass die Interpretation eines Prädikats durch entsprechende Teilmengen sich in der Mengenlehre ganz natürlich ergibt.
Wie können wir nun mit Hilfe einer Interpretation herausfinden, ob eine Aussage wahr oder falsch bezüglich dieser Interpretation ist?
Beginnen wir mit den Termen. Zur Erinnerung: Terme sind sind Variablen und Konstanten oder Kombinationen daraus, gebildet über Funktionsbezeichner. In der Peano-Arithmetik sind z.B. \(x \cdot y\) , \( x + y \) sowie \( x^* \) Terme. In der Mengenlehre sind nur Variablen und Konstanten Terme, da es dort keine Funktionsbezeichner gibt.
Die Interpretation eines Terms gewinnen wir dadurch, dass wir alle darin vorkommenden Konstanten, Variablen und Funktionen durch ihre Interpretationen ersetzen, also durch Elemente der Domäne \( D_J \) und durch Funktionen von \( D_J \times ... \times D_J \) nach \( D_J \). Die Interpretation eines Terms ist damit selbst ein Element der Domäne oder eine Funktion über der Domäne.
Nun macht es keinen Sinn, von wahren oder falschen Termen zu sprechen, denn ein Term wie \(x \cdot y\) ist weder wahr noch falsch, sondern er stellt eine Funktion dar, die aus zwei Objekten \(x\) und \(y\) ein neues Objekt \(x \cdot y\) macht. Daher müssen wir noch einen Schritt weiter gehen und aus Termen mit Hilfe von Prädikatsbezeichnern elementare Ausdrücke wie z.B. \( x \cdot y = 0 \) bilden.
Wann ist ein solcher elementarer Ausdruck wahr oder falsch? Wenn Variablen wie bei \( x \cdot y = 0 \) vorhanden sind, hängt der Wahrheitswert dieses Ausdrucks natürlich davon ab, welche konkreten Elemente der Domäne \( D_J \) wir für die Variablen einsetzen. Für jede mögliche Kombination der einzelnen Variablen wird es also einen eigenen Wahrheitswert des Ausdrucks geben. Dazu müssen wir die Interpretationen der Variablenwerte (also die konkreten Elemente von \( D_J \) ) in die beteiligten Terme einsetzen, den Wert der Terme berechnen (das Ergebnis sind wieder bestimmte Elemente von \( D_J \) ) und am Schluss nachsehen, ob diese berechneten Terme das Prädikat erfüllen, ob also die Term-Ergebnisse (hintereinander als geordnetes Paar oder Tupel geschrieben) in der Teilmenge von \( D_J \times ... \times D_J \) liegen, die die Interpretation des Prädikats darstellt. Wenn das so ist, dann ist der elementare Ausdruck für diese Variablenwerte in der vorliegenden Interpretation wahr, andernfalls ist er falsch.
Ein einfaches Beispiel: Betrachten wir den elementaren Ausdruck \( x = y \). Die beiden Terme in diesem Ausdruck lauten einfach \(x\) und \(y\) (d.h. sie sind reine Variablen). Wir wollen nun wissen, ob dieser Ausdruck für \(x = 0\) und \( y = 0^* = 1 \) wahr oder falsch ist bezogen auf die Standardinterpretation (also bezogen auf das von-Neumannsche Modell der natürlichen Zahlen mit \( D_J = \mathbb{N} = \{ \varnothing, \{ \varnothing \} , \{ \varnothing , \{ \varnothing \} \} , ... \} \) , siehe Kapitel 4.2). Dazu setzen wir für \(x\) den Wert \( i_J(0) = \varnothing \) und für \(y\) den Wert \( i_J^*(0) = \{ \varnothing \} \) ein. Das Gleichheitsprädikat ist gegeben durch die Teilmenge \( \{ (x,y) \in \mathbb{N} \times \mathbb{N} ; \, x = y \} \) , also durch \( \{ ( \varnothing , \varnothing ) , \, ( \{ \varnothing \} , \{ \varnothing \} ), \, ... \} \) . Wie wir sehen, gehört \( ( \varnothing, \{ \varnothing \} ) \) nicht dazu, d.h. der Ausdruck \( x = y \) ist in dieser Interpretation für diese Variablenwerte falsch. Das war Ihnen und mir natürlich sofort klar, dass \( 0 = 1 \) falsch sein muss.
Nun können wir mit Hilfe der logischen Symbole wie \( \land, \neg \) usw. aus den elementaren Ausdrücken größere zusammengesetzte Ausdrücke aufbauen und nach deren Wahrheitswert (bezogen auf die Interpretation \(J\) ) fragen. Um den Wahrheitswert dieser Ausdrücke zu definieren, legen wir folgendes fest (dabei sind \(B\) und \(C\) ebenfalls Ausdrücke, z.B. elementare Ausdrücke):
Und hier sind die versprochenen Wahrheitstabellen (dabei steht 0 für falsch und 1 für wahr):
| \( \, B \, \) | \( \, \neg B \, \) |
| 0 | 1 |
| 1 | 0 |
| \( \, B \, \) | \( \, C \, \) | \( \, B \land C \, \) | \( \, B \lor C \, \) | \( \, B \Rightarrow C \, \) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Die meisten Einträge entsprechen unmittelbar unserem anschaulichen Verständnis der Begriffe \( \land \) (also und) , \( \lor \) (also das inklusive oder) und \( \neg \) (also nicht bzw. Gegenteil).
Lediglich bei den Tabelleneinträgen zu \( \Rightarrow \) (also impliziert oder daraus folgt) muss man etwas überlegen. Nur im Fall, dass \(B\) wahr und \(C\) falsch ist, ist unmittelbar klar, dass \( B \Rightarrow C \) falsch sein muss, denn aus etwas Wahrem soll nicht etwas Falsches folgen.
Wie aber sieht es in den anderen Fällen aus? Wenn \(B\) falsch ist, dann hat \( B \Rightarrow C \) keine unmittelbar anschauliche Bedeutung (denn was folgt schon aus etwas falschem), und wenn \(B\) und \(C\) wahr sind, dann ist uns nicht klar, ob \(C\) auch aus \(B\) folgt.
Um unseren logischen Apparat möglichst einfach zu halten, ist aber dennoch die Definition von Wahrheitswerten von \( B \Rightarrow C \) wünschenswert. Einen dritten Wahrheitswert, der "unbestimmt" bedeutet, haben wir allerdings in dieser Version der Logik nicht vorgesehen, so dass wir uns für wahr oder falsch entscheiden müssen. Diese Entscheidung haben wir in den Wahrheitstabellen so vorgenommen, dass \( B \Rightarrow C \) nur genau dann falsch ist, wenn \(B\) wahr ist, aber \(C\) falsch ist. In den Fällen, wo wir also anschaulich unsicher über den Wahrheitswert von \( B \Rightarrow C \) sind, sagen wir einfach, \( B \Rightarrow C \) ist wahr (denn wir haben keinen Grund, es definitiv als falsch anzusehen). Im Zweifel also für den Angeklagten!
Mit Hilfe der Wahrheitstabellen kann man zeigen, dass die ersten sechs oben genannten logischen Axiome immer den Wahrheitswert wahr annehmen, unabhängig vom Wahrheitswert von \(B, C\) und \(D\) (nicht zuletzt deshalb haben wir die Wahrheitswerte von \( B \Rightarrow C \) auch gerade so wie oben gewählt). Man bezeichnet diese Axiome auch als die Axiome des klassichen logischen Propositionenkalküls (auch Aussagenkalkül oder Aussagenlogik genannt. Diese Axiome entsprechen also immer wahren Aussagen, so wie wir das von Axiomen auch erwarten. Dabei ist die Wahrheit dieser logischen Axiome sogar unabhängig von der jeweiligen Interpretation – man kann sagen, diese Axiome drücken immer eine Wahrheit aus.
Wie steht es mit der Schlussfolgerungsregel (Modus Ponens), die es einem erlaubt, aus den beiden Zeichenketten \(B\) und \(B \Rightarrow C\) die Zeichenkette \(C\) zu erzeugen? Man kann mit den Wahrheitstabellen zeigen, dass wenn \(B\) und \(B \Rightarrow C\) beide wahr sind, dann auch \(C\) wahr ist. Die Wahrheit von \(B\) und \(B \Rightarrow C\) überträgt sich also auf die neue Aussage \(C\). Dasselbe gilt auch für die Generalisierungsregel und die Existenzregel. Es passt also alles wunderbar zusammen.
An dieser Stelle taucht eine interessante Frage auf: Angenommen, jemand gibt uns eine Aussage, z.B. \( ((B \Rightarrow C) \land D) \Rightarrow (B \lor D)) \Rightarrow C \). Ist diese Aussage immer wahr, unabhängig vom Wahrheitswert von \(B, C\) und \(D\)? Um diese Frage zu klären, kann man versuchen, die Aussage aus den logischen Axiomen mit Hilfe der Schlussfolgerungsregel herzuleiten und sie damit zu beweisen. Das kann bei langen Aussagen sehr mühsam sein.
Man kann aber statt dessen auch die Wahrheitstabellen nehmen und mit ihrer Hilfe den Wahrheitswert der Aussage für alle Wahrheitswert-Kombinationen der darin vorkommenden elementaren Ausdrücke \(B, C, D \) usw. einfach berechnen. Bei wenigen elementaren Ausdrücken ist das sicher leicht durchführbar. Bei großen Aussagen mit z.B. 30 elementaren Ausdrücken darin wird diese Berechnung jedoch sehr aufwendig, denn \( 2^{30} \) (also mehr als 1 000 000 000) Wahrheitswert-Kombinationen müssten berechnet werden. Diese Berechnung wäre nur dann effizienter als die Suche nach einem Beweis, wenn es einen sehr guten Algorithmus dafür gäbe. Wir werden auf diese Frage bei der Betrachtung des Begriffs NP-Vollständigkeit in einem späteren Kapitel noch zurückkommen.
Die Definition der allgemeinen Wahrheit einer Aussage (bezogen auf eine Interpretation \(J\)) kann extrem nicht-konstruktiv sein, wenn die Domäne \( D_J \) unendlich groß ist. Dies ist z.B. bei den natürlichen Zahlen der Fall. Um beispielsweise den Wahrheitswert von Aussagen wie \( x + y = y + x \) oder \( \forall x : B(x) \) zu berechnen, müssen wir unendlich viele Werte für \(x\) bzw. \(x\) und \(y\) einsetzen. Insofern haben wir zwar den Begriff der Wahrheit definiert, aber der Wahrheitswert einer Aussage lässt sich nicht immer einfach durch Ausprobieren ermitteln. Und in der Tat gibt es ja selbst heute noch Aussagen über die natürlichen Zahlen, deren Wahrheitswert nicht bekannt ist. So besagt die berühmte Goldbachsche Vermutung, dass sich jede gerade Zahl, die größer als 2 ist, als Summe von zwei Primzahlen ausdrücken lässt. Die gerade Zahl 20 ist zum Beispiel die Summe aus den beiden Primzahlen 13 und 7. Keiner weiß, ob diese Vermutung immer zutrifft – ein Gegenbeispiel ist nicht bekannt. Wir kommen auf die Goldbachsche Vermutung in einem späteren Kapitel noch einmal ausführlich zurück.
Das Problem, den Wahrheitswert einer Aussage zu bestimmen, hindert uns nicht daran, zu definieren, wann wir eine Aussage als immer wahr bezeichnen wollen:
|
Ob die Goldbachsche Vermutung immer wahr ist, wissen wir also bis heute nicht (auch wenn vieles dafür spricht).
Es gibt sogar Aussagen, die immer wahr unter allen Interpretationen sind. Wir haben oben solche Aussagen bereits kennengelernt (z.B. das logische Axiom \( B \Rightarrow (C \Rightarrow (B \land C)) \) ). Wir wollen solche Aussagen als logisch richtig (engl.: logically valid) oder auch als universell wahr bezeichnen (auch der Begriff Tautologie wird oft verwendet). Diese Definition von logisch richtigen Aussagen kann sehr nicht-konstruktiv sein, denn man muss nicht nur prüfen, ob die Aussage immer wahr ist, sondern man muss dies sogar für alle im Rahmen der Zermelo-Fränkel-Mengenlehre denkbaren Interpretationen tun. Bei manchen Aussagen wie z.B. den logischen Axiomen kann der Nachweis allerdings dennoch geführt werden, weil deren Wahrheitswert nicht vom Wahrheitswert der darin enthaltenen elementaren Aussagen abhängt.
Wie wir wissen, besitzt ein formales System wie die Peano-Arithmetik neben den logischen Axiomen von oben eine Reihe weiterer Axiome, die die Eigenschaften der vom System beschriebenen Objekte genauer festlegen sollen. In der Peano-Arithmetik sind das die Peano-Axiome (siehe Kapitel 2.1). Wir verlangen nun von einer Interpretation \(J\), dass alle diese Axiome immer wahr unter dieser Interpretation sind (alle oben genannten logischen Axiome sind sowieso immer wahr, wie man beweisen kann). Da sich durch die Schlussfolgerungsregel (Modus Ponens), die Generalisierungsregel und die Existenzregel die Wahrheitswerte der Axiome auch auf die daraus ableitbaren Aussagen übertragen (siehe oben), sind damit auch alle diese ableitbaren Aussagen wahr unter der Interpretation \(J\). Das formale System produziert also nur wahre Aussagen (bezogen auf die gewählte Interpretation).
Wir haben oben bereits gesagt, dass bestimmte logische Axiome logisch richtig sind, also immer wahr unter allen Interpretationen sind. Man kann zeigen, dass dies für alle oben dargestellten Axiome der Logik gilt, und dass die Umwandlungsregeln (Schlussfolgerungsregel, Generalisierungsregel und Existenzregel) aus logisch richtigen Aussagen immer nur wieder logisch richtige Aussagen erzeugen. Es gilt also:
|
Die Frage ist aber, ob die logischen Axiome und die Umwandlungsregeln ausreichen, um alle logisch richtigen Aussagen daraus herzuleiten. Lässt sich jede Aussage, die immer wahr unter allen Interpretationen ist, aus den logischen Axiomen mit Hilfe der Umwandlungsregeln ableiten? Die Antwort auf diese Frage lautet: JA!, wie Kurt Gödel im Jahr 1929 bewies (also nur ein Jahr bevor er seinen berühmten Unvollständigkeitssatz veröffentlichte):
Gödels Vollständigkeitssatz der klassischen Logik:
|
Man kann Gödels Vollständigkeitssatz als Rechtfertigung für die logischen Axiome und die Umwandlungsregeln ansehen. Die Regeln und Axiome sind vollständig in dem Sinn, dass sich jede logisch richtige (also universell wahre) Aussage damit beweisen lässt. Mehr kann man von einem formalen System der Logik kaum erwarten!
Es ist an dieser Stelle wichtig, zu erkennen, dass Gödels Vollständigkeitssatz nicht behauptet, jede in einer bestimmten Interpretation \(J\) wahre Aussage sei beweisbar. Es wird nur behauptet, dass jede Aussage, die in jeder Interpretation wahr ist, auch beweisbar ist und umgekehrt. Nach Gödels Unvollständigkeitssatz gibt es in jedem hinreichend mächtigen formalen System auch Aussagen, die in einer Interpretation \(J\) wahr und in einer anderen Interpretation \(J'\) falsch sind (siehe Kapitel 2.4 und 2.5). Diese Aussagen sind in diesem System dann nicht beweisbar, denn sie gehören nicht zu den logisch richtigen (d.h. universell wahren) Aussagen.
Damit hat man auch ein gutes Werkzeug in der Hand, um die
Unabhängigkeit einer Aussage von den Axiomen des formalen Systems zu zeigen:
Man konstruiert ein Modell des formalen Systems, in dem diese Aussage wahr ist,
und ein anderes Modell, in dem diese Aussage falsch ist.
Dazu hat man verschiedene Techniken entwickelt.
So kann man von einem Modell ausgehen und versuchen, es so zu verkleinern, dass es zu einer
zuvor unentscheidbare Aussage keine Gegenbeispiele mehr gibt. Man spricht von einem
inneren Modell.
So ein Modell hat Gödel im Jahr 1938 für die Kontinuumshypothese konstruiert.
Dieses Modell enthält garantiert keine Gegenbeispiele zur Kontinuumshypothese mehr, d.h. diese ist
in dem Modell wahr. Umgekehrt kann man ein gegebenes Modell auch erweitern, also ein
äußeres Modell konstruieren – das bezeichnet man auch als
Forcing (Erzwingen
von Wahrheit oder Falschheit unentscheidbarer Aussagen).
Auf diese Weise hat P.Cohen im Jahr 1963
ein äußeres Modell der ZFC-Mengenlehre konstruiert, in dem die Kontinuumshypothese falsch ist
(wobei man aber kein explizites Gegenbeispiel angeben kann, sondern nur zeigen kann, dass
es in dem Modell eines gibt). Übrigens kann man auch ein äußeres Modell
konstruieren, in dem die Kontinuumshypothese wahr ist.
Man kann also durch eine geeignete Modellerweiterung die Kontinuumshypothese
gleichsam ein- und ausschalten.
Mehr dazu siehe Ralf Schindler:
Wozu brauchen wir große Kardinalzahlen?

In einem Modell \(J\) sind die Axiome des formalen Systems immer wahr, denn sonst wäre es kein Modell. Die Regeln der Logik können daraus dann nur weitere Aussagen ableiten, die ebenfalls immer wahr in dem Modell \(J\) sind. Das Gegenteil einer solchen Aussage wäre in dem Modell \(J\) dann falsch und kann demnach nicht abgeleitet werden. Widersprüche sind also ausgeschlossen, wenn ein formales System ein Modell \(J\) hat. Es gilt also:
|
Um die Widerspruchsfreiheit zu beweisen, kann man also stattdessen auch beweisen, dass das formale System ein Modell hat. Genau das werden wir weiter unten für die Peano-Arithmetik auch tun! Was aber geschieht, wenn wir ein Modell der Mengenlehre aufstellen wollen? Da die Mengenlehre nicht ihre eigene Widerspruchsfreiheit beweisen kann, kann sie auch nicht beweisen, dass es ein Modell von ihr gibt – höchstens vielleicht dann, wenn man die Widerspruchsfreiheit als Annahme hineinsteckt (mehr dazu gleich). Daher wird es uns auch nicht wundern, dass weiter unten die Modelle der Mengenlehre nicht-konstruktiv sind. Gäbe es ein sehr konkretes Modell der Mengenlehre zum Anfassen, so wäre damit zugleich die Widerspruchsfreiheit der Mengenlehre bewiesen, und zwar durch eine Modellkonstruktion mit den Mitteln der Mengenlehre.
Wie sieht es mit der Umkehrung des obigen Satzes aus? Folgt aus der Widerspruchsfreiheit eines formalen Systems \(L\) erster Ordnung, dass es ein Modell \(J\) (eine Interpretation) innerhalb der Mengenlehre gibt? Da die Mengenlehre eines der mächtigsten bekannten mathematischen Systeme ist, liegt dieser Gedanke tatsächlich nahe, denn ansonsten hätte die Mengenlehre ja deutliche Löcher: Sie könnte nicht als Modell für formale Systeme dienen. Wie sich herausstellt, lautet die Antwort folgendermaßen:
Modellexistenzsatz:
|
Es gibt also zu jedem widerspruchsfreien formalen System, das die oben dargestellte Sprache der Logik erster Ordnung verwendet, garantiert eine Interpretation im Rahmen der Mengenlehre, also ein Modell! Darin zeigt sich erneut die große Ausdruckskraft der Mengenlehre als grundlegendes formales System für die klassische Mathematik.
Der Modellexistenzsatz sagt, dass die (syntaktische) Widerspruchsfreiheit eines formalen Systems erster Ordnung ausreicht, es als mathematisch bedeutungstragend anzusehen, denn es beschreibt eine gewisse mathematische Struktur, die sich in der Mengenlehre ausdrücken lässt. Über die Nützlichkeit dieser Struktur ist damit natürlich noch nichts ausgesagt.
Mit Hilfe des Modellexistenzsatzes lässt sich Gödels Vollständigkeitssatz der klassischen Logik relativ leicht beweisen. Den Beweis kann man z.B. bei Karlis Podnieks finden (siehe Literaturangabe unten).
Wie aber beweist man den Modellexistenzsatz? Nun, dieser Beweis ist ein schwieriges und einfallsreiches Stück Mathematik, und es würde viel zu weit führen, hier darauf einzugehen (ich kenne die Details im Übrigen auch nicht – eine Beweisskizze findet man wieder bei Karlis Podnieks, siehe unten). Wir wollen uns nur für folgende Frage interessieren: Wird in dem Beweis eine Konstruktionsvorschrift für das Modell (die Interpretation) des formalen Systems angegeben, d.h. kann man die Interpretation wirklich explizit konstruieren?
Leider ist das nicht der Fall, und nach unseren obigen Überlegungen überascht uns das auch nicht. In dem Beweis werden zwar viele Bestandteile der Interpretation konstruiert (z.B. die Domäne \(D_J\), die Menge der Axiome oder die Interpretation der Funktionsbezeichner), aber bei der Interpretation der Prädikatsbezeichner ist der Beweis nicht-konstruktiv. Der Modellexistenzsatz behauptet also lediglich die Existenz eines Modells, ohne zu sagen, wie man das Modell konstruieren kann. Dies erinnert an andere nicht-konstruktive Aussagen in der Mengenlehre wie z.B. das Auswahlaxiom. Die Existenz eines Modells ist also zunächst nur im schwachen Sinn gesichert (d.h. die Annahme der Nichtexistenz führt zu einem Widerspruch), aber es bleibt offen, ob man es wirklich konstruieren kann. In manchen Fällen funktioniert es (z.B. bei der Peano-Arithmetik), aber gelingt die Konstruktion in allen Fällen? Was geschieht beispielsweise, wenn man innerhalb der Zermelo-Fränkel-Mengenlehre versucht, ein Modell der Zermelo-Fränkel-Mengenlehre zu konstruieren? Ein solches Modell muss es nach dem Modellexistenzsatz geben, wenn die Mengenlehre widerspruchsfrei ist. Wir kommen etwas weiter unten auf diese Frage zurück.
Ursprünglich wurde der Modellexistenzsatz im Jahr 1915 und 1919 in einer etwas schwächeren Form durch Leopold Löwenheim und Thoralf Skolem bewiesen:
Löwenheim-Skolem-Theorem:
|
Das Löwenheim-Skolem-Theorem benötigt als Voraussetzung also die Existenz eines Modells. Daher ist der Modellexistenzsatz etwas allgemeiner als das Löwenheim-Skolem-Theorem, denn der Modellexistenzsatz fordert nur die Widerspruchsfreiheit und nicht die Existenz eines Modells (was Widerspruchsfreiheit zur Folge hat).
Worin liegt die Ursache dafür, dass es immer ein abzählbares Modell gibt? Letztlich liegt dies daran, dass es generell immer nur abzählbar viele Beschreibungen für alles geben kann, denn man muss die Beschreibung aufschreiben und dafür irgendeine Sprache verwenden. Die Ausdrücke und Sätze jeder Sprache lassen sich aber immer der Größe nach alphabetisch auflisten und so abzählen. Ein Modell muss also gewährleisten, dass in ihm abzählbar viele Sätze wahr sind, und dafür genügt offenbar auch ein abzählbares Modell. Nur die Aussagen und Objekte (beispielsweise Funktionen), die sich explizit im Rahmen des formalen Systems ausdrücken lassen, können in das Modell übertragen werden. Das sind nur abzählbar viele Objekte, und daher reicht auch ein abzählbares Modell. Und das alles, auch wenn es abstrakt gesehen vielleicht überabzählbar viele Objekte in dem formalen System gibt.
Was geschieht nun, wenn wir versuchen, ein Modell der Zermelo-Fränkel-Mengenlehre innerhalb der Zermelo-Fränkel-Mengenlehre aufzustellen? Kann dieses Modell abzählbar sein, obwohl die Zermelo-Fränkel-Mengenlehre in der Lage ist, überabzählbare Mengen zu konstruieren (z.B. die reellen Zahlen)? Man spricht in diesem Zusammenhang von Skolems Paradoxon:
Skolems Paradoxon:
|
Im abzählbaren Modell der Mengenlehre gibt es nur abzählbare Mengen, obwohl die Mengenlehre die Existenz nicht-abzählbarer Mengen beweist. Dennoch sind im abzählbaren Modell alle beweisbaren Aussagen der Mengenlehre wahr, also auch die Aussage, dass es nicht-abzählbare Mengen gibt. Ist das nicht ein Widerspruch? Könnte das ein Zeichen dafür sein, dass die Mengenlehre selbst Widersprüche enthält, so dass der Modellexistenzsatz gar nicht gilt? Bricht damit unser Fundament der Mathematik in sich zusammen, so wie dies bei Cantors ursprünglicher Form der Mengenlehre der Fall war (siehe Kapitel 4.1)?
Wir müssen hier sehr vorsichtig mit vorschnellen Schlussfolgerungen sein. Daher wollen wir uns sehr genau ansehen, worin das Paradoxon besteht, und ob es sich um ein wirkliches oder nur ein scheinbares Problem handelt.
Also: Bezeichnen wir das abzählbare Modell der Mengenlehre, das es nach dem Modellexistenzsatz geben soll, zunächst einmal mit \(J\). Die Mengenlehre selbst bezeichnen wir mit ZFC (für Zermelo-Fränkel-Mengenlehre mit Auswahlaxiom (axiom of choice)). Innerhalb von ZFC können wir beweisen, dass die Menge \( \mathbb{R} \) der reellen Zahlen nicht-abzählbar ist. Formal bedeutet das, dass wir in ZFC aus den Axiomen eine Aussage herleiten können, die folgendes sagt:
wobei \( \mathbb{N} \) die natürlichen Zahlen sind (in der formalen Sprachen von ZFC entspricht diese Aussage natürlich einem recht komplizierten Ausdruck, der nur die erlaubten Sprachelemente von ZFC enthält). Statt eins-zu-eins-Funktion schreibt man auch bijektive Funktion.
Was geschieht nun, wenn wir von ZFC zum abzählbaren Modell \(J\) (das sich natürlich selbst innerhalb von ZFC befindet) übergehen? Im Modell \(J\) sind die Interpretationen der Mengen \( \mathbb{R} \) und \( \mathbb{N} \) nun Teilmengen der abzählbaren Menge \( D_J\), d.h. \( \mathbb{R}_J \) und \( \mathbb{N}_J \) sind abzählbare Mengen. Man kann daher innerhalb von ZFC (das ja den Rahmen des Modells bildet) folgende Aussage herleiten:
denn zwischen zwei abzählbaren Mengen gibt es immer eine eins-zu-eins-Funktion (denn beide Mengen lassen sich eins-zu-eins der Menge \( \mathbb{N} \) der natürlichen Zahlen zuordnen).
Wie aber lautet im Modell \(J\) die Interpretation der obigen Aussage \( \neg \exists f : \, f \) ist eine eins-zu-eins-Funktion von \( \mathbb{R} \) nach \( \mathbb{N} \) , die aussagt, dass die Menge \( \mathbb{R} \) der reellen Zahlen nicht abzählbar ist? Sie lautet so:
Was bedeutet das? Schauen wir uns dazu noch einmal an, was beim Übersetzen einer Funktion \(f\) in das Modell \(J\) passiert: Jede Funktion \(f\) wird in der Mengenlehre durch einen länglichen formalen Ausdruck dargestellt, der als einziges Prädikat \( \in \) enthält. Aus \( \in \) wird beim Übergang zum Modell eine entsprechende Teilmenge von \( D_J \times D_J \) . Welche Teilmenge das ist, legt letztlich den Charakter des Modells entscheiden fest. Auf diese Weise entsteht zu jeder Funktion \(f\) schließlich ebenfalls eine entsprechende Modellmenge \(f_J\) , die eine Teilmenge von \( \mathbb{R}_J \times \mathbb{N}_J \) ist.
Und nun sagt der obige Satz: Beim Übersetzen aller (aufschreibbaren)
bijektiven Funktionen \(f\) von \( \mathbb{R} \) nach \( \mathbb{N} \)
in solche Teilmengen \(f_J\)
von \( \mathbb{R}_J \times \mathbb{N}_J \) entsteht keine einzige Teilmenge,
die eine Eins-zu-Eins-Beziehung zwischen \( \mathbb{R}_J \) nach \( \mathbb{N}_J \) herstellt.
Das ist irgendwie beruhigend, denn es gab ja auch vor der Übersetzung in das Modell
keine Funktion \(f\), die eine Eins-zu-Eins-Beziehung
zwischen \( \mathbb{R} \) und \( \mathbb{N} \) hergestellt hat.
Diese Eigenschaft überträgt sich auf das Modell, so wie man es auch naiv erwarten würde.
Natürlich gibt es Funktionen, die eine Eins-zu-Eins-Beziehung
zwischen \( \mathbb{R}_J \) nach \( \mathbb{N}_J \)
herstellen, beispielsweise unser \(g\) von oben. Aber eine solche
Funktion entsteht beim Übersetzen der Mengenlehre in das abzählbare Modell nicht.
Die Funktion \(g\) gehört nicht zum Modell dazu!
Offenbar kann man innerhalb des Modells keine Funktion zum Abzählen der Modellmenge \( \mathbb{R}_J \)
finden, außerhalb des Modells dagegen schon.
Das ist die bekannte Standardlösung für Skolems Paradoxon. Beim genauen Hinsehen trifft sie allerdings nur für die sogenannten transitiven Modelle zu. Was bedeutet das?
In einem Modell ist zunächst nur gewährleistet, dass die formalen Ausdrücke \( \neg, \Rightarrow \) und \( = \) analog zur üblichen Mengenlehre interpretiert werden. Bei den Quantifizierern \( \forall \) und \( \exists \) sowie bei dem Prädikat \( \in \) muss das nicht so sein. So haben wir oben die Quantifizierer auch auf das Modell eingeschränkt interpretiert, also beispielsweise als es gibt in dem Modell. Möglich ist aber auch, dass das Prädikat \( \in \) im Modell keine Mengenzugehörigkeit mehr bedeutet. Wir erinnern uns: Aus \( \in \) wird in dem Modell eine Teilmenge von \( D_J \times D_J \) , also eine Menge mit geordneten Mengenpaare \( (a,b) \) mit \(a, b\) aus der Modelldomäne \( D_J \). Ein solches Paar \( (a,b) \) aus dieser Teilmenge ist die Interpretation des formalen Strings \( a \in b \) aus der Mengenlehre innerhalb des Modells. Im Modell muss aber die Modellmenge \(a\) nicht wirklich ein Element der Modellmenge \(b\) sein – man spricht dann von einem nicht-transitiven Modell der Mengenlehre. Tatsächlich gibt es abzählbare Modelle der Mengenlehre, die \( \in \) nicht wie gewohnt interpretieren. Hier ist es nicht der Quantifizierer \( \exists \) , der anders interpretiert wird, sondern in einem solchen nicht-transitiven Modell wird beispielsweise eine bijektive Funktion zwischen den Modellmengen nicht als bijektiv interpretiert.
Zum Glück gibt es aber auch abzählbare transitive Modelle der Mengenlehre, bei denen das Paar \( (a,b) \) (welches das Prädikat \( a \in b \) interpretiert) auch bedeutet, dass die Modellmenge \(a\) Element der Modellmenge \(b\) ist. Das sind die Modelle, die man üblicherweise betrachtet. In diesem Fall greift unsere obige Standardlösung, bei der wir den formalen Ausdruck \( \exists \) im Modell als es gibt in dem Modell interpretiert haben. Die \( \in \) -Relation ist in dem Modell dann einfach die Einschränkung der üblichen \( \in \) -Relation auf die Mengen der Modelldomäne. Analog besteht dann auch die Modellmenge \( \mathbb{R}_J \) der reellen Zahlen einfach aus den reellen Zahlen innerhalb der Modelldomäne. Da aber trotz dieser Einschränkung ein Modell der ZFC-Mengenlehre vorliegt, glaubt das Modell natürlich, dass \( \mathbb{R}_J \) überabzählbar ist, denn es besitzt keine Funktion zum Abzählen von \( \mathbb{R}_J \). Mehr zu diesem Thema siehe z.B. Timothy Bays: The Mathematics of Skolem's Paradox und Ralf Schindler: Wozu brauchen wir grosse Kardinalzahlen?
Machen wir uns noch einmal klar, was hier geschieht: Die Mengenlehre ist in der Lage, einen Satz zu beweisen, den wir interpretiert haben als "es gibt überabzählbar viele reelle Zahlen". Daher erwarteten wir naiv, dass in jedem Modell die Modelldomäne \( D_J \) eine überabzählbare Menge ist, denn sie soll ja die Interpretationen der reellen Zahlen enthalten.
Genau genommen tut die Mengenlehre jedoch etwas anderes:
Sie beweist einen sehr komplexen Ausdruck, in dem nur die wenigen Sprachelemente
der Mengenlehre (z.B. \( \in \) usw.) vorkommen und den wir als
\( \neg \exists f : \, f \) ist eine eins-zu-eins-Funktion von \( \mathbb{R} \) nach \( \mathbb{N} \)
gedeutet haben.
Der Modellexistenzsatz sagt nun, dass es eine Interpretation der Mengenlehre
(innerhalb der Mengenlehre) gibt, in der die Modelldomäne \( D_J \)
abzählbar ist und in der die Interpretation des obigen komplexen Ausdrucks
dennoch wahr ist. Das bedeutet, dass wir den komplexen Ausdruck nicht einfach
in jeder Interpretation als "es gibt überabzählbar viele reelle Zahlen"
verstehen können. In dem abzählbaren Modell bedeutet er etwas anderes,
beispielsweise dass es innerhalb des Modells keine Funktion gibt,
die dieses Abzählen übernehmen könnte, oder dass das Modell eine solche Funktion nicht als
bijektiv erkennt.
Innerhalb des abzählbaren Modells ist es deshalb möglich, eine nicht-abzählbaren Menge
gleichsam zu simulieren.
Formale Systeme, die über reelle Zahlen zu sprechen scheinen, können also so interpretiert werden, dass in der Interpretation nur abzählbar viele Objekte vorkommen! Man kann Skolems Paradoxon vielleicht als Hinweis auf eine Lücke zwischen Form (Syntax) und Inhalt (Semantik) auffassen. Das erinnert uns sehr an die Überaschung, die wir bei der Peano-Arithmetik erlebt haben: Die Peano-Arithmetik erster Ordnung, die wir geschaffen hatten, um die natürlichen Zahlen zu beschreiben, konnte auch so interpretiert werden, dass sie über andere Objekte spricht (nämlich über die übernatürlichen Zahlen, die sich durch spezielle Mengen veranschaulichen lassen, siehe Kapitel 3.1).
Halten wir also fest:
|
Bei den natürlichen Zahlen ist das anders: diese können von der Mengenlehre in eindeutiger Weise eingefangen werden, denn alle Modelle der natürlichen Zahlen (gegeben durch die Peano-Aussagen) sind isomorph zueinander (siehe den Isomorphiesatz von Dedekind am Schluss von Kapitel 4.2). Die Peano-Arithmetik konnte das noch nicht (siehe Kapitel 3.1 und 2.1). Wir sind darauf am Schluss von Kapitel 4.2 bereits kurz eingegangen und wollen uns dieses Phänomen im Folgenden noch etwas genauer ansehen:
Wiederholen wir dazu noch einmal die wesentlichen Ergebnisse aus Kapitel 4.2 zur Modellierung der natürlichen Zahlen im Rahmen der Mengenlehre:
Isomorphiesatz von Dedekind (auch Categoricity Theorem genannt):
|
Dabei versteht man unter Mengendarstellungen der natürlichen Zahlen jedes Modell, bei dem die folgenden Peano-Aussagen wahr sind: \begin{align} & 0 \in \mathbb{N} \\ & \forall n: \, (n \in \mathbb{N} ) \Rightarrow ( n^* \in \mathbb{N} ) \\ & \forall n: \, (n \in \mathbb{N} ) \Rightarrow \neg( n^* = 0 ) \\ & \forall n, m: \,[ \, (m, n \in \mathbb{N} ) \, \land \, ( m^* = n^* ) \, ] \Rightarrow [m = n] \\ & \forall A: \, [ \, (0 \in A) \, \land \, \forall n : \, [(n \in \mathbb{N}) \Rightarrow \\ & \quad \quad \quad ( (n \in A) \Rightarrow ( n^* \in A)) \, ]] \Rightarrow [ \mathbb{N} \subseteq A ] \end{align} (die zusätzlichen Aussagen für Addition und Multiplikation schreiben wir nicht mehr explizit auf, sondern nehmen sie im Geiste mit hinzu). Dabei ist \( \mathbb{N} \) gleich der Modelldomäne \(D_J\).
Die letzte Aussage bezeichnet man auch als Induktionsaussage oder Induktionsaxiom. Seine Bedeutung wird besonders klar, wenn wir für \(A\) eine Teilmenge von \( \mathbb{N} \) nehmen. Wenn dann für diese Menge \(A\) die eckige Klammer gilt, dann muss auch \( \mathbb{N} \) eine Teilmenge von \(A\) sein, d.h. \( \mathbb{N} \) und \(A\) müssen identisch sein. Man kann die Induktionsaussage auch so formulieren, dass man \( A \subseteq \mathbb{N} \) zusätzlich voraussetzt und als Folgerung \( \mathbb{N} = A \) herausbekommt.
Im Rahmen der Mengenlehre haben wir bei der Induktionsaussage ein \( \forall A : ... \) vorangestellt, denn aus Sicht der Mengenlehre ist dies eine erlaubte Konstruktion erster Ordnung (die Menge \(A\) ist ja eine Variable in der Sprache der Mengenlehre). Jede Teilmenge \(A\) entspricht dabei einer Eigenschaft, die gewisse natürliche Zahlen aufweisen können. Das Axiom erfasst damit überabzählbar viele Eigenschaften der natürlichen Zahlen, denn es gibt überabzählbar viele Teilmengen der natürlichen Zahlen (wir hatten oben bereits kurz darüber gesprochen; der Beweis kann leicht mit Cantors Diagonalmethode geführt werden, siehe in Kapitel 3.5 die Konstruktion der Diagonalmenge \( V = \{ n ; \, n \notin D_n \} \). Genau diese Tatsache bewirkt, dass die Mengenlehre die natürlichen Zahlen so eindeutig modellieren kann! Warum ist das so?
Schauen wir uns zum Vergleich die Axiome der Peano-Arithmetik (ohne Mengenlehre, d.h. erster Ordnung) an:
(wieder nehmen wir die zusätzlichen Aussagen für Addition und Multiplikation implizit mit hinzu). Dabei ist insbesondere das letzte Axiom (das Induktionsaxiom) wieder interessant, denn es handelt es sich (anders als bei der Induktions-Aussage der Mengenlehre) um ein Axiomenschema: Man muss irgendeine wohlgeformte Aussage \(A\) (mit einer freien Variablen) in der Sprache der Peano-Arithmetik vorgeben. Alle diese Aussagen lassen sich in einer unendlich langen Liste (z.B. nach Größe und Alphabet sortiert) aufführen, so dass man eine entsprechende Induktions-Axiomenliste aufstellen kann. Dabei kann man aber immer nur abzählbar viele Eigenschaften der natürlichen Zahlen erfassen. Da es aber überabzählbar viele Eigenschaften der natürlichen Zahlen gibt (repräsentiert durch die entsprechenden Teilmengen), muss es Eigenschaften der natürlichen Zahlen geben, die nicht in der Axiomenliste vorkommen. Die Axiomenliste hat nicht-stopfbare Löcher.
Sind diese Löcher schlimm, oder handelt es sich um einen unbedeutenden Schönheitsfehler?
Aus Kapitel 3.1 wissen wir, dass es Nicht-Standard-Modelle für die Peano-Arithmetik erster Ordnung gibt: die sogenannten übernatürlichen Zahlen. Diese Zahlen sind keine Zahlen im üblichen Sinn, sondern sie können im Rahmen eines Modells innerhalb der Mengenlehre durch spezielle Mengen (genauer: durch unendlich lange Zahlenfolgen) dargestellt werden. So stellt z.B. die Zahlenfolge \( y = (1, 2, 3, 4, 5, 6, ...) \) eine übernatürliche Zahl \(y\) dar, die größer ist als jede natürliche Zahl. Der Nachfolger dieser Zahl wäre dann \( y + 1 = (2, 3, 4, 5, 6, 7, ...) \).
Das Induktionsaxiom der Peano-Arithmetik verhindert die Existenz solcher übernatürlicher Zahlen also offenbar nicht: Wenn eine Aussage \(A(0)\) gilt, und wenn aus der Aussage \(A(n)\) die Aussage \(A(n^*)\) folgt, so ist es durchaus möglich, dass die Aussage \(A(n)\) für alle natürlichen und für alle übernatürlichen Zahlen gilt. Es wird nicht erzwungen, dass sich jede Zahl der Peano-Arithmetik als mehrfacher Nachfolger der Null schreiben lässt. Die Möglichkeit, dass sich fremde Eindringlinge (übernatürliche Zahlen) in das Reich der natürlichen Zahlen einschleichen, kann nicht ausgeschlossen werden! Warum das so ist, sehen wir etwas weiter unten.
Gilt dies auch für die Induktionsaussage im Rahmen der Mengenlehre, in der die Mengen \(A\) die Aussagen \(A\) ersetzt? Gibt es auch hier fremde Eindringlinge in der Menge \( \mathbb{N} \), die sich nicht als mehrfacher Nachfolger der Null schreiben lassen?
Der Isomorphiesatz von Dedekind zeigt, dass es sie nicht gibt, denn alle Modelle der Peano-Aussagen sind zueinander isomorph und damit auch isomorph zum von Neumannschen Modell (auch Standardmodell genannt, siehe Kapitel 4.2), in dem jedes Element von \mathbb{N} als mehrfacher Nachfolger der Null geschrieben werden kann.
Den Grund dafür kann man relativ leicht einsehen:
Beginnen wir mit dem Standardmodell der Peano-Aussagen, also mit der Menge \[ \mathbb{N} = \{0, 1, 2, 3, ... \} \] mit
|
Dabei ist die Nachfolgerfunktion definiert durch \( n^* = n \cup \{n\} \) , d.h. \(n^*\) enthält alle Elemente des Vorgängers \(n\) und zusätzlich den Vorgänger \(n\) selbst als neues Element.
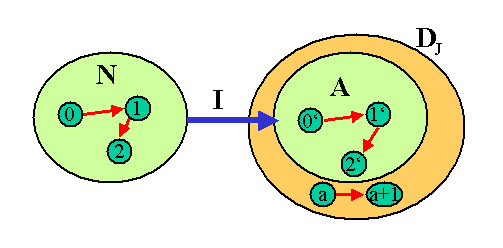
Nun wollen wir von diesem Modell zu irgendeinem anderen Modell der Peano-Aussagen übergehen. Dafür brauchen wir eine neue Modellmenge \( \mathbb{N}' \), ein Element \(0'\) dieser Menge (das die Rolle der Null übernehmen soll) und eine Nachfolgerfunktion \( ()^* \) darin, die nicht unbedingt genauso aussehen muss wie im obigen Standardmodell. In dem neuen Modell gelten alle Peano-Aussagen (sonst wäre es kein Modell dafür).
Um eine Verbindung zwischen dem Standardmodell und dem neuen Modell zu erhalten, definieren wir eine Abbildung \(I\) von \( \mathbb{N} \) nach \( \mathbb{N}' \), die aus dem Standardmodell das neue Modell machen soll. \(I\) wird rekursiv über die Eigenschaften \begin{align} 0' &= I(0) \\ (I(n))^* &= I(n^*) \end{align} festgelegt. Man kann zeigen, dass \(I\) eine bijektive (d.h. umkehrbar eindeutige) Abbildung ist, und dass \(I\) mit den Peano-Aussagen verträglich ist (siehe Karlis Podnieks: About Model Theory).
Was uns interessiert, ist die Frage, ob jedes Element der neuen Modellmenge \( \mathbb{N}' \) durch die Abbildung \(I\) aus einem passenden Element der Standard-Modellmenge \( \mathbb{N} \) erzeugt wird, oder ob es Elemente im neuen Modell gibt, die kein Urbild (keine Vorlage) im Standardmodell haben. Solche Elemente wären dann fremde Eindringlinge (übernatürliche Zahlen), die sich nicht unbedingt als mehrfacher Nachfolger von \(0'\) schreiben lassen.
Zunächst einmal wissen wir, dass sich \(0'\) aus \(0\) erzeugen lässt, denn \(0' = I(0)\) (so war \(I\) definiert). Weiter wissen wir: Wenn ein Element \( n' \in \mathbb{N}' \) ein Urbild \(n \in \mathbb{N}\) hat (d.h. es gibt ein \(n \in \mathbb{N}\), so dass \(n' = I(n)\) ist), dann hat auch sein Nachfolger \( (n')^* \) ein Urbild in \( \mathbb{N} \), denn \( (n')^* = (I(n))^* = I(n^*) \) .
Die Induktionsaussage muss nun auch für unsere neue Modellmenge \( \mathbb{N}' \) gelten: \begin{align} & \forall A: \, [ \, (0' \in A) \, \land \, \forall n' : \, [(n' \in \mathbb{N}') \Rightarrow \\ & \quad \quad \quad ( (n' \in A) \Rightarrow ( (n')^* \in A)) \, ]] \Rightarrow [ \mathbb{N}' \subseteq A ] \end{align} Da diese Aussage für alle Mengen \(A\) gilt, muss sie auch für die spezielle Menge \(A\) gelten, die aus allen Elemente der neuen Modellmenge \( \mathbb{N}' \) besteht, die ein Urbild in \( \mathbb{N} \) haben: \[ A := \{ n' \in \mathbb{N}' ; \, \exists n: \, (n \in \mathbb{N}) \land (n' = I(n) \} \] \(A\) ist also eine Teilmenge der neuen Modellmenge \( \mathbb{N}' \) (nämlich die mit Urbild in \( \mathbb{N} \) ). Wie wir oben gesehen haben, ist dann \(0' \in A\), denn \(0'\) hat das Urbild \(0\) in \( \mathbb{N} \). Dann haben wir oben noch gesehen: Wenn \(n' \in A \) ist (also ein Urbild hat), so ist auch \( (n')^* \in A \) (hat also auch ein Urbild). Damit sind die Voraussetzungen in der Induktionsaussage erfüllt und es folgt \( \mathbb{N}' \subseteq A \). Zugleich war nach Konstruktion \( A \subseteq \mathbb{N}' \) sodass \( \mathbb{N}' = A \) ist. Jedes Element der neuen Modellmenge \(\mathbb{N}'\) hat ein entsprechendes Urbild in \(\mathbb{N}\). Die beiden Modelle sind isomorph.
Daraus folgt nun, dass sich auch im neuen Modell \( \mathbb{N}' \) jedes Element als mehrfacher Nachfolger der Null (also von \(0'\)) schreiben lässt, denn dies ist auch im Standardmodell \(\mathbb{N}\) der Fall. Ein Beispiel: Nehmen wir an, \(n' = I(0^*) \). Dann folgt \(n' = I(0^*) = (I(0))^* = (0')^* \), d.h. \(n'\) ist der einfache Nachfolger von \(0'\). Analog kann man auch bei längeren Nachfolger-Ketten vorgehen, denn jedes Element der neuen Modellmenge \( \mathbb{N}' \) hat ja ein aufgrund der Induktionsaussage ein Urbild im Standardmodell \( \mathbb{N} \), das dort ein ggf. mehrfacher Nachfolger der \(0\) ist. Wir sehen: Die Induktionsaussage verhindert, dass es fremde Eindringlinge in der neuen Modellmenge \( \mathbb{N}' \) gibt, die sich nicht als mehrfacher Nachfolger von \(0'\) schreiben lassen. Übernatürliche Zahlen sind damit verhindert.
Warum aber verhindert das Induktionsaxiom der Peano-Arithmetik nicht ebenso das Auftauchen solcher fremden Eindringlinge?
Schauen wir uns das Induktionsaxiom der Peano-Arithmetik noch einmal an: \[ [ A(0) \, \land \, (\forall n : (A(n) \Rightarrow A(n^*) )] \Rightarrow \, [ \forall n : (A(n) ] \] Wir können dieses Axiom in die Sprache der Mengenlehre übersetzen, indem wir eine Modellmenge \(D_J\) für die Peano-Axiome wählen und für jede Aussage \(A(n)\) eine Teilmenge \(A\) der Modellmenge definieren, die diejenigen Elemente der Modellmenge enthält, für die die Aussage \(A(n)\) wahr ist: \[ A := \{ n \in D_J , \, A(n) \text{ ist wahr im Modell } J \} \] (die Menge bezeichnen wir einfach mit demselben Buchstaben wie die Aussage der Peano-Arithmetik; also nicht verwirren lassen!).
Wenn wir das Induktionsaxiom der Peano-Arithmetik nun wieder auf Mengen übertragen, so erfasst dieses diesmal nicht alle Mengen \(A\) (also nicht mehr \( \forall A \) ), sondern nur diejenigen Teilmengen von \( D_J \), die sich wie oben aus Aussagen der Peano-Arithmetik konstruieren lassen. Da sich aber diese Aussagen abzählen lassen (also in einer unendlichen Liste aufführen lassen), kann hier die Induktionsaussage auch nur für abzählbar viele Teilmengen \(A\) von \( D_J \) gelten. Es gibt aber überabzählbar viele Teilmengen von \( D_J \), denn \( D_J \) ist eine unendliche Menge (wenn auch selbst ggf. abzählbar), sonst könnte sie keine Modellmenge für die Peano-Axiome sein (analog gibt es überabzählbar viele Teilmengen von \(\mathbb{N}\)).
Es kann also Teilmengen der Modellmenge \( D_J \) geben, für die die obige Induktionsaussage nicht gilt. Ob es diese Teilmengen gibt, hängt von der Wahl der Modellmenge \( D_J \) ab. In dem Fall, dass es keine solchen Teilmengen gibt, ist \( D_J \) isomorph zum Standardmodell mit der Modellmenge \( \mathbb{N} \), wie wir oben gesehen haben. In diesen Modellen gibt es keine übernatürlichen Zahlen.
Was geschieht nun, wenn \( D_J \) Teilmengen enthält, für die die Induktionsaussage nicht gilt?
Wir können erneut versuchen, wie oben eine Abbildung \(I\) zu definieren, die eine Verbindung zwischen dem Standardmodell mit Modellmenge \( \mathbb{N} \) und dem Modell mit Modellmenge \( D_J \) herstellt. \(I\) wird dabei wieder rekursiv über die Eigenschaften \(0' = I(0)\) und \( (I(n))^* = I(n^*) \) festgelegt.
Lässt sich wieder jedes Element der Modellmenge \( D_J \) durch die Abbildung \(I\) aus einem passenden Element der Standard-Modellmenge \( \mathbb{N} \) erzeugen?
Wir können versuchen, die obige Argumentation zu wiederholen und eine Menge \(A\) als Abbild der Menge \( \mathbb{N} \) unter der Abbildung \(I\) zu konstruieren. Alle Elemente in \(A\) lassen sich dann wieder als mehrfacher Nachfolger von \(0'\) schreiben.
Wenn für diese Menge \(A\) die Induktionsaussage gilt (da sie sich zugleich aus einer Aussage der Peano-Arithmetik konstruieren lässt), dann ist \(A = D_J\) und das Modell ist isomorph zum Standardmodell.
Es kann aber geschehen, dass für \(A\) die Induktionsaussage nicht gilt, d.h.
\(A\) entspricht keiner Menge, die in der Modellmenge \(D_J\) durch eine entsprechende
Aussage der Peano-Arithmetik ausgewählt werden kann. In diesem Fall können wir
die Schlussfolgerung \(A = D_J\) nicht ziehen. Die Modellmenge \(D_J\)
kann Elemente außerhalb von \(A\) enthalten, die sich nicht als Nachfolger von \(0'\)
schreiben lassen. Diese Elemente repräsentieren dann die übernatürlichen Zahlen.
Wir sehen also, dass die Peano-Arithmetik ein nicht-stopfbares Loch hat, da sie nicht alle Eigenschaften der natürlichen Zahlen (so wie sie durch Teilmengen definierbar sind) erfassen kann. Das Induktionsaxiom erfasst nur abzählbar viele Eigenschaften (und damit nur abzählbar viele Teilmengen), so dass Modelle konstruierbar sind, in denen das Induktionsaxiom nicht für alle Teilmengen der Modellmenge gilt. Diese Modelle sind dann nicht mehr isomorph zum Standardmodell.
Man könnte auf die Idee kommen, den Mangel der Peano-Arithmetik zu beseitigen, indem man das Induktionsaxiom folgendermaßen umformuliert (wir hatten diese Möglichkeit weiter oben bereits kurz erwähnt): \begin{align} \forall A : [[ A(0) \, & \land \,(\forall n : (A(n) \Rightarrow A(n^*) )] \\ & \Rightarrow \, [ \forall n : (A(n) ] ] \end{align} Der Unterschied zum ursprünglichen Axiom liegt darin, dass wir nun \( \forall A \) vorangestellt haben, also das Induktionsaxiom formal für alle Aussagen \(A\) fordern. Dies ist allerdings im Rahmen der Logik erster Ordnung nicht erlaubt, da \(A\) in der Peano-Arithmetik keine Variable ist, sondern eine Eigenschaft von Variablen. Man bezeichnet daher einen solchen Ausdruck als Ausdruck zweiter Ordnung (wir sind oben bereits kurz darauf eingegangen). Um solche Ausdrücke zu ermöglichen, kann man versuchen, die Logik erster Ordnung zu einer Logik zweiter Ordnung zu erweitern. Es zeigt sich jedoch, dass sich eine solche Logik nicht axiomatisieren lässt. Eine zufriedenstellende Lösung des Problems ist das nicht! Formale Systeme zweiter Ordnung sind nur dann wirklich greifbar, wenn man sie als Modell in einem umfassenderen System erster Ordnung (z.B. der Mengenlehre) formuliert, denn dann erhält der Ausdruck \( \forall A \) die klare Bedeutung "für alle Teilmengen der Modelldomäne gilt". Wir wollen daher auf Logik zweiter Ordnung hier nicht näher eingehen.
Wie grundlegend sind nun die natürlichen Zahlen in der Mathematik? Im neunzehnten Jahrhundert versuchte man, die Mathematik auf der Grundlage der natürlichen Zahlen und der Logik (erster Ordnung) aufzubauen. Die natürlichen Zahlen galten als das grundlegende Fundament, auf dem man die übrige Mathematik (z.B. die reellen Zahlen) aufbauen wollte. Leopold Kronecker (1823 bis 1891) sagte dazu: "Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk." Unsere Betrachtung der Peano-Arithmetik (erster Ordnung) oben zeigt jedoch, dass die Logik (erster Ordnung) sowie die Peano-Axiome nicht das Ziel erreichen, das sie erreichen sollen: eine eindeutige Charakterisierung der natürlichen Zahlen.
Um die natürlichen Zahlen eindeutig zu charakterisieren, muss man über die Peano-Arithmetik hinausgehen und mächtigere mathematische Begriffe verwenden. Innerhalb der Mengenlehre ist es dann sehr wohl möglich, die natürlichen Zahlen eindeutig (bis auf Isomorphien) zu erfassen: Sie werden als Mengen definiert, die den Peano-Aussagen genügen. Die Mengenlehre ist aber auch in der Lage, die reellen Zahlen zu definieren. Um die natürlichen Zahlen eindeutig zu definieren, braucht man also ein formales System, das auch über reelle Zahlen reden kann. Die natürlichen Zahlen eignen sich daher nicht als alleinige Grundlage für die Mathematik.
Man sieht hier sehr schön, dass man sich nicht wie der berühmte Baron Münchhausen selbst an den Haaren aus dem Sumpf ziehen kann. Doch genau das versuchen Axiomensysteme: sich an den eigenen Haaren aus dem Sumpf zu ziehen. Die Begriffe in Axiomensystemen werden nämlich nur implizit durch ihre Verwendung in den Axiomen definiert in der Hoffnung, ihre Bedeutung dadurch möglichst genau zu spezifizieren. Ein Axiomensystem versucht, seine Bedeutung aus sich selbst heraus zu begründen. Die Peano-Arithmetik versucht dies durch die Peano-Axiome für die natürlichen Zahlen, und sie scheitert letztlich, da sie übernatürliche Zahlen nicht verhindern kann.
Erst ein umfassenderes System wie die Mengenlehre kann die natürlichen Zahlen
vollständig erfassen: in ihr sind alle Modelle der Peano-Aussagen isomorph, also
gleichwertig. Als umfassenderes System ist die Mengenlehre aber auch in der Lage, weit mehr
als die natürlichen Zahlen zu beschreiben. Dennoch wird diese Ausdruckskraft benötigt,
denn ein System wie die Peano-Arithmetik, das nur auf die natürlichen Zahlen zugeschnitten ist,
reicht nicht aus. Es gibt sogar mathematische Aussagen über natürliche Zahlen innerhalb der Peano-Arithmetik,
die man nicht innerhalb der Peano-Arithmetik beweisen kann, wohl aber innnerhalb der Mengenlehre!
Es gibt hier eine Interessante Parallele zur Philosophie: Was ist in der Philosophie die Definition eines neuen Begriffs (z.B. des Begriffs "natürliche Zahl")? Plato hatte dazu die folgende Idee:
Man benennt also zuerst die Zugehörigkeit zum Allgemeinen (die Gattung), und weist dann auf den spezifischen Unterschied hin, der das jeweilige Objekt von allen anderen Objekten der Gattung unterscheidet. Ein Beispiel aus dem juristischen Umfeld: Unter Abfall versteht man alle beweglichen Güter, derer sich der Besitzer endgültig entledigen will. Die Verallgemeinerung (die Gattung) sind hier die beweglichen Güter, und die positive Abgrenzung erfolgt durch die Eigenschaft, dass sich der Besitzer dieser Güter endgültig entledigen will.
Auf genau diese Weise definiert man auch innerhalb der Mengenlehre die natürlichen Zahlen. Die natürlichen Zahlen sind alle die Mengen (das ist die Gattung), die die Peano-Aussagen erfüllen (das ist die positive Abgrenzung). Auf diese Weise erhält man eine (bis auf Isomorphien) eindeutige Definition der natürlichen Zahlen.
Diese Vorgehensweise der Definition durch Verallgemeinerung und positive Abgrenzung hat allerdings ein Problem: wie sind die verallgemeinerten Begriffe (die Gattungen) definiert, auf die man sich in der Definition bezieht? An irgendeiner Stelle kommt man zu Begriffen, die sich nicht durch weitere Verallgemeinerung definieren lassen. Man muss dann diese Begriffe anders definieren, z.B. implizit durch ihre Verwendung in einem Axiomensystem. Genau so ist der Begriff der Menge definiert: er wird durch Axiome (beispielsweise die Zermelo-Fränkel-Axiome) implizit beschrieben.
Bei der Peano-Arithmetik führte eine solche implizite Definition der Begriffe durch ihre Verwendung in Axiomen allerdings zu dem Problem der Uneindeutigkeit: die implizite Definition entspricht nicht unbedingt der beabsichtigten Bedeutung (Stichwort: übernatürliche Zahlen). Leidet die umfassendere Mengenlehre, die ja implizit durch die Zermelo-Fränkel-Axiome beschrieben ist, an demselben Problem?
Wie wir oben bereits gesehen haben, ist das tatsächlich der Fall (Skolems Paradoxon), denn es gibt abzählbare Modelle der Mengenlehre! So ist die Mengenlehre nicht in der Lage, die reellen Zahlen in eindeutiger Weise einzufangen, denn es gibt verschiedene Modelle der Mengenlehre (und damit der dadurch beschriebenen reellen Zahlen), die nicht gleichwertig (isomorph) zueinander sind. Vermutlich könnte erst ein noch umfassenderes System als die Mengenlehre diesen Mangel beheben, denn innerhalb dieses Systems ließe sich dann der Mengenbegriff im Sinne Platos durch Verallgemeinerung und positive Abgrenzung definieren. Allerdings hätte dann dieses umfassendere System vermutlich wieder denselben Mangel. Es bleibt schwierig, sich an den eigenen Haaren aus dem Sumpf zu ziehen!
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 15 March 2023