
Quelle: Wikipemia Commons File:Georg Friedrich Bernhard Riemann.jpeg, gemeinfrei
Die Riemannsche Vermutung ist vielleicht das berühmteste und wichtigste ungelöste Problem der Mathematik. Seine Lösung ist eine Million US-Dollar wert. Letztlich geht es bei der Riemannschen Vermutung darum, die multiplikativen Grundbausteine der natürlichen Zahlen zu verstehen: die Primzahlen. Kann man ihre Verteilung im Meer der natürlichen Zahlen verstehen? Wie lange muss man weiterzählen, bis die nächste Primzahl kommt? Warum erscheint die jeweils nächste Primzahl wie zufällig mal bereits nach wenigen Schritten, mal dagegen erst nach großem Abstand? Gibt es hier vielleicht ein verstecktes Muster?
Riemann gelang es mit Hilfe der komplexen Zahlen, die Verteilung der Primzahlen in eine mathematische Landschaft über einer zweidimensionalen Ebene zu übersetzen: die sogenannte Zeta-Funktion (\(\zeta\)-Funktion). Die Topographie dieser Landschaft enthält dabei das gesamte Wissen über die Primzahlen. Insbesondere genügt es, die Punkte auf Meereshöhe (die Nullstellen) zu kennen, um die gesamte Landschaft rekonstruieren zu können. Daher enthalten die Nullstellen alle Informationen über die Verteilung der Primzahlen. Riemann entwickelte eine konkrete Formel, um aus den Nullstellen die Verteilung der Primzahlen zurückzugewinnen. Dabei wirkt jede Nullstelle wie die Quelle für eine sich ausbreitende Welle, die man sich wie einen akustischen Ton vorstellen kann. Die Töne aller Nullstellen überlagern sich zur Verteilung der Primzahlen. Dabei ist eine Nullstelle umso lauter, je weiter östlich (rechts von der y-Achse) sie liegt, und ihr Ton ist umso höher, je weiter nördlich (oberhalb der x-Achse) sie liegt.
Zu seiner Überaschung fand Riemann, dass alle von ihm berechneten Nullstellen gleich laut sind, und dass die Tonleiter der beitragenden Töne bis zu beliebig hohen Tönen weitergeht. Die (unendlich vielen) Punkte auf Meereshöhe (die eine Lautstärke größer als Null besitzen) liegen scheinbar alle auf einer Geraden parallel zur y-Achse, die rechts neben der y-Achse in einem Abstand von 1/2 zu dieser Achse verläuft. Es gibt nur ein Problem: Weder Riemann noch sonst irgendjemand konnte dies bis heute beweisen! Man spricht daher von der Riemannschen Vermutung.
Die Riemannsche Vermutung behauptet also, dass tatsächlich jede der unendlich vielen tongebenden Nullstellen auf dieser Geraden liegt, d.h. dass alle Töne in der Musik der Primzahlen gleich laut sind. Dies würde bedeuten, dass man sich die Primzahlverteilung tatsächlich in gewissem Sinn wie zufällig gewürfelt vorstellen kann: Man geht alle natürlichen Zahlen durch und würfelt jedesmal, ob man die aktuelle Zahl als Primzahl ansehen möchte. Dabei hängt die Wahrscheinlichkeit, mit der der Würfel Primzahl anzeigt, von der aktuellen Zahl ab (denn Primzahlen werden bei größeren Zahlen immer seltener). Natürlich würde man auf diese Weise nicht die wirklichen Primzahlen finden, aber die statistischen Eigenschaften unserer gewürfelten Primzahlverteilung wären dieselben wie bei der tatsächlichen Primzahlverteilung.
Es geht also in diesem Kapitel um eines der wohl berühmtesten offenen Rätsel der Mathematik: die Riemannschen Vermutung. Wie das P =? NP-Problem aus dem vorhergehenden Kapitel gehört auch die Riemannsche Vermutung zu den sieben Millenium Prize Problems, und ein Beweis ist wieder eine Millionen US-Dollar wert (siehe auch CMI: Riemann Hypothesis).
Die Riemannsche Vermutung gehörte bereits vor über 100 Jahren zu den wichtigsten mathematischen Problemen. Hilbert sagte dazu in seinem berühmten Vortrag (gehalten auf dem internationalen Mathematiker-Kongress zu Paris 1900):
8. Primzahlenprobleme
In der Theorie der Verteilung der Primzahlen sind in neuerer Zeit durch Hadamard, de la Vallée Poussin, v. Mangoldt und Andere wesentliche Fortschritte gemacht worden. Zur vollständigen Lösung der Probleme, die uns die Riemannsche Abhandlung "Über die Anzahl der Primzahlen unter einer gegebenen Größe" gestellt hat, ist es jedoch noch nötig, die Richtigkeit der äußerst wichtigen Behauptung von Riemann nachzuweisen, dass die Nullstellen der Function \(\zeta(s)\), die durch die Reihe \[ \zeta(s) = 1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \, ... \] dargestellt wird, sämtlich den reellen Bestandteil \( \frac{1}{2} \) haben – wenn man von den bekannten negativ ganzzahligen Nullstellen absieht. Sobald dieser Nachweis gelungen ist, so würde die weitere Aufgabe darin bestehen, die Riemannsche unendliche Reihe für die Anzahl der Primzahlen genauer zu prüfen und insbesondere zu entscheiden, ob die Differenz zwischen der Anzahl der Primzahlen unterhalb einer Größe \(x\) und dem Integrallogarithmus von \(x\) in der Tat von nicht höherer als der \( \frac{1}{2} \)-ten Ordnung in \(x\) unendlich wird, und ferner, ob dann die von den ersten komplexen Nullstellen der Function \(\zeta(s)\) abhängengen Glieder der Riemannschen Formel wirklich die stellenweise Verdichtung der Primzahlen bedingen, welche man bei den Zählungen der Primzahlen bemerkt hat.
.....
Ok – das ist nicht ganz einfach zu verstehen, und wir werden uns da schrittweise herantasten. Immerhin sehen wir jetzt schon, dass die Riemannsche Vermutung etwas mit den Nullstellen einer bestimmten Funktion \(\zeta(s)\) zu tun hat, und dass diese Funktion eine Verbindung zu Primzahlen aufweist. Viele Beweise der Zahlentheorie, aber auch Beweise in anderen mathematischen Bereichen enthalten heute Sätze wie "Unter der Voraussetzung, dass die Riemannsche Vermutung zutrifft ...". Sogar die moderne Physik scheint bei Themen wie Quantenchaos oder Energieniveaus von Atomkernen Berührungspunkte mit der Riemannschen Vermutung zu haben.
Um eine anschauliche Vorstellung von der Bedeutung der Riemannschen
Vermutung zu bekommen, wollen wir uns genauer mit den Primzahlen beschäftigen,
so wie der berühmte deutsche Mathematiker
Bernhard Riemann dies vor etwa 150 Jahren getan hat.

Quelle:
Wikipemia Commons File:Georg Friedrich Bernhard Riemann.jpeg, gemeinfrei
Primzahlen sind natürliche Zahlen, die sich ohne Rest nur durch 1 und durch sich selbst teilen lassen. Die ersten Primzahlen lauten
wobei wir eine (recht große) Lücke nach 97 gelassen haben. Im Jahr 2018 war die größte bekannte Primzahl die Zahl \[ 2^{82.589.933} - 1 \] Als Dezimalzahl ausgeschrieben ist dies eine Zahl mit 24.862.048 Dezimalstellen. Wenn Sie dieses Kapitel lesen, gibt es vielleicht schon wieder eine noch größere Primzahl – die Rekorde fallen hier relativ schnell. Auf Wikipedia: Primzahl finden Sie die aktuellen Infos dazu.
Bereits der antike griechische Mathematiker Euklid kannte vor 2300 Jahren den Beweis dafür, dass es unendlich viele Primzahlen gibt. Wir wollen den relativ einfachen Beweis hier überspringen.
Primzahlen erscheinen wie zufällig zwischen den anderen Zahlen verstreut zu sein. Dabei macht man die Beobachtung, dass Primzahlen immer seltener werden, je größer die betrachteten Zahlen sind. Folgen Primzahlen vielleicht annähernd einem Verteilungsgesetz, so wie dies statistische Größen (z.B. die Summe der gezogenen Lottozahlen einer Ziehung) tun?
Fragen dieser Art ließen sich leicht beantworten, wenn man eine relativ einfache Rechenformel (nennen wir sie \(f\)) finden könnte, mit der man die n-te Primzahl (nennen wir sie \(p_n\)) einfach berechnen kann: \[ p_n = f(n) \] Dann wäre \( f(1)=2, \; f(2)=3, \; f(3)=5, \; ... \) . Gibt es eine solche einfache Rechenformel?
Seit 1912 weiß man, dass ein nichtkonstantes Polynom mit rationalen Koeffizienten keine solche Formel liefern kann, denn für unendlich viele Werte von \(n\) liefert ein solches Polynom nicht-prime Werte. Gibt es also noch andere Kandidaten für die Primzahl-Rechenformel?
Eine einfache Formel der Form \( p_n = f(n) \) ist mir nicht bekannt. In Kapitel 3.5 haben wir allerdings gesehen, dass es ein Polynom 25ten Grades mit 26 natürlichen Variablen gibt, dessen positive Werte gerade die Menge der Primzahlen ergibt. Meistens allerdings ist der Wert des Polynoms negativ. Nur für ganz bestimmte Werte-Kombinationen der 26 natürlichen Variablen ist das Polynom positiv und ergibt dann eine Primzahl. Diese Werte-Kombinationen für die 26 Variablen zu finden ist dabei die eigentliche Aufgabe. Man kann diese Kombinationen durch Lösen eines komplizierten Gleichungssystems ermitteln. Der dazu notwendige Rechenaufwand ist jedoch enorm, so dass sich dieses Verfahren nicht zur tatsächlichen Berechnung von Primzahlen eignet. Daher liefert auch dieses Verfahren keine einfache Formel zur Berechnung von Primzahlen.
Zurück zu unserer Frage:
Oder anders gefragt:
Wie viele Primzahlen befinden sich also beispielsweise im Bereich zwischen 1.000.000.000 und 2.000.000.000 ?
Bei kleinen Zahlenbereichen helfen hier natürlich die verfügbaren Tabellen der bisher berechneten Primzahlen weiter. Irgendwann jedoch stoßen diese Tabellen an ihre Grenzen, und einen halbwegs brauchbaren Algorithmus, um sie weiterzuführen, gibt es nicht. Es gibt jedoch relativ effiziente Wege, auch ohne genaue Kenntnis der Primzahlen die Anzahl Primzahlen in großen Zahlenbereichen zu berechnen.
Um die weitere Diskussion zu vereinfachen, wollen wir die folgende Schreibweise einführen:
So gibt es z.B. 4 Primzahlen, die kleiner-gleich 10 sind (nämlich die Primzahlen 2, 3, 5 und 7), d.h. \(\pi(10) = 4\). Analog gibt es 9 Primzahlen, die kleiner-gleich 25 sind, d.h. \(\pi(25) = 9\). Wie viele Primzahlen gibt es nun, die größer als 10 sind und kleiner-gleich 25? Die Antwort lautet \( \pi(25) - \pi(10) = 9 - 4 = 5 \) (nämlich die Zahlen 11, 13, 17, 19 und 23). Die Funktion \(\pi(x)\) ermöglicht es uns also, die Anzahl Primzahlen innerhalb beliebiger Zahlenintervalle anzugeben.
Die folgende Grafik zeigt die Funktion \(\pi(x)\) bis \(x = 60\):
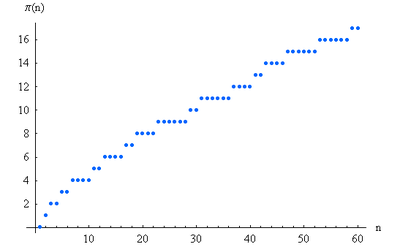
Quelle: Wikimedia Commons File:PrimePi.PNG,
Public Domain
Man sieht in dieser Grafik sehr schön, wie immer wieder eine neue Primzahl hinzukommt, so dass \(\pi(x)\) an diesen Stellen um Eins ansteigt. Die entsprechenden Stufen sind dabei recht zufällig verteilt, d.h. es ist schwierig, vorherzusagen, wann genau eine neue Primzahl hinzukommt. Insgesamt sieht man aber doch, dass die Stufen einem gewissen Verteilungsgesetz zu folgen scheinen. Man hat den Eindruck, als ob man \(\pi(x)\) durch irgendeine glatte Kurve wenigstens annähernd beschreiben (approximieren) kann, besonders wenn man größere Zahlenbereiche in den Blick nimmt.
Eine solche glatte (d.h. stetig-differenzierbare) Funktion \(f(x)\) kann zwar nicht die einzelnen Stufen der Primzahlfunktion \(\pi(x)\) im Detail erfassen, aber sie sollte doch wenigstens annähernd deren Verlauf wiedergeben, besonders für große \(x\), bei denen die einzelnen Stufen kaum noch ins Gewicht fallen. Mit einer solchen Funktion könnten wir beispielsweise Schätzwerte von \(\pi(x)\) für besonders große Werte von \(x\) ermitteln, für die sich \(\pi(x)\) selbst nicht mehr exakt angeben lässt. So könnten wir beispielsweise abschätzen, wie viele Primzahlen es bis zur Zahl \(2^{1.000.000.000}\) gibt, obwohl unsere Liste der bekannten Primzahlen schon bei viel kleineren Zahlen aufhört und wir sie deshalb nicht mehr einzeln abzählen können (siehe die größte bekannte Primzahl oben).
Was aber meinen wir mit approximieren genau? Die Idee ist, dass für große \(x\)-Werte der prozentuale Unterschied zwischen \(\pi(x)\) und der approximierenden Funktion \(f(x)\) immer kleiner wird. Er soll beliebig klein werden, wenn wir nur \(x\) genügend groß werden lassen. Wichtig ist dabei, dass wir über den prozentualen (also den relativen) Unterschied reden, und nicht über den absoluten! Das bedeutet: Nicht \( |f(x) - \pi(x)| \) soll klein werden, sondern \( \frac{|f(x) - \pi(x)|}{\pi(x)} \) . Anders ausgedrückt: \(\frac{f(x)}{\pi(x)}\) soll für große \(x\) beliebig nahe an 1 heranrücken. Halten wir also fest:
Ein Beispiel: Die Normalparabel \(g(x) = x^2\) lässt sich durch die Funktion \(f(x) = x^2 + x \) (das ist eine leicht nach links unten verschobene Parabel) approximieren, denn \[ \frac{f(x)}{g(x)} = \frac{x^2 + x}{x^2} = 1 + \frac{1}{x} \] nähert sich für große \(x\) immer mehr an 1 an. Der relative Unterschied wird immer kleiner, der absolute Unterschied (der gleich \(x\) ist) dagegen nicht.
Gibt es nun Funktionen, mit denen man \(\pi(x)\) in diesem Sinn approximieren kann?
Im Lauf der Zeit fand man einige Kandidaten, bei denen der Vergleich mit Tabellen von \(\pi(x)\) nahelegte, dass man mit ihnen die Primzahlfunktion approximieren könnte. Ein solcher Kandidat ist die einfache Funktion \( \frac{x}{\ln (x)} \), wobei \(\ln (x)\) der natürliche Logarithmus von \(x\) (zur Basis \(e\) = 2,71828182845904) ist. Häufig bezeichnet man diese Beobachtung auch als den Primzahlsatz:
Auf den Beweis dieser Beobachtung gehen wir erst weiter unten ein, d.h. streng genommen müssten wir momentan noch von einer Primzahl-Vermutung sprechen.
Nun ist \( \frac{x}{\ln (x)} \) nicht der einzige Kandidat. Beispielsweise kann man stattdessen auch die Funktion \( \frac{x}{\ln (x) - c} \) nehmen, wobei \(c\) eine beliebige relle Zahl ist. Die Zahl \(c\) fällt nämlich für große \(x\) immer weniger ins Gewicht, so dass sie das asymptotische Verhalten für große \(x\) nicht beeinflusst. Daher können wir auch sagen:
In dieser Form wurde der Primzahlsatz zum ersten mal im Jahr 1798 von Legendre erwähnt. Legendre versuchte dabei, die Zahl \(c\) so zu bestimmen, dass die Approximation auch für kleinere \(x\) möglichst gut mit den damals bekannten Werten von \(\pi(x)\) übereinstimmte. Er erhielt den Wert \(c = 1,08366\) . Heute weiß man, dass der einfache Wert \(c = 1\) am besten funktioniert.
Ein anderer Kandidat stammt von dem großen deutschen Mathematiker Carl Friedrich Gauß (vermutlich aus dem Jahr 1791, zum ersten mal erwähnt in einem Brief von Gauß an den Astronom Hencke im Jahr 1849 und zuerst veröffentlicht im Jahr 1863):
Ausschnitt aus einem Gemälde von Gottlieb Biermann, 1887,
Quelle:
Wikimedia Commons File:Carl Friedrich Gauss.jpg , gemeinfrei.
Oft wird das Integral auch von 0 statt von 2 an genommen, wobei dann noch eine Vorschrift hinzugefügt werden muss, wie mit dem Pol bei 1 umzugehen ist (denn \(\ln (1) = 0 \) ). Für große \(x\)-Werte und damit für das asymptotische Verhalten von \( \mathrm{Li}(x) \) spielt das jedoch keine Rolle. Wir verwenden hier generell das Integral von 2 bis \(x\).
Die Funktion \( \mathrm{Li}(x) \) lässt sich nicht durch andere elementare Funktionen
als geschlossene Formel ausdrücken. Deshalb ist die einzige präzise Möglichkeit,
sie direkt über das Integral anzugeben. \( \mathrm{Li}(x) \) ist also die Fläche unter der Funktion
\( \frac{1}{\ln (t)} \) von \(t = 2\) bis \(t = x\) :
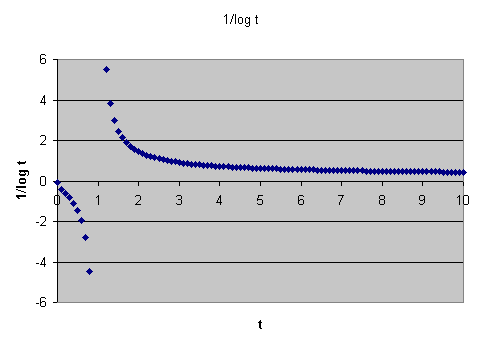
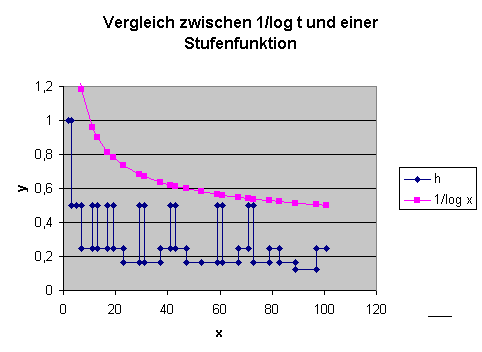
Wie man sieht, handelt es sich bei \( \mathrm{Li}(x) \) um eine sehr einfache Funktion, die sich leicht mit Computern berechnen lässt. Dass eine Approximation für die Primzahlfunktion \( \pi(x) \) über eine Fläche unter der Funktion \( \frac{1}{\ln (t)} \) zustande kommen kann, dafür liefert der folgende Gedankengang eine anschauliche Interpretation: Man trage auf der \(x\)-Achse alle Primzahlen ein. Zwischen je zwei Primzahlen zeichnet man nun eine Stufe ein, so dass der Flächeninhalt dieser Stufe gleich 1 ist. Die \(y\)-Höhe einer Stufe, die von der Primzahl \(p_n\) bis zur Primzahl \(p_{n+1}\) geht, ist also gleich \( \frac{1}{p_{n+1} - p_n} \) . Die Gesamtfläche unter dieser Stufenfunktion von 2 bis \(x\) ist dann (bis auf den Rest der letzten angefangenen Stufe, den man noch hinzunehmen muss) gleich der Anzahl Primzahlen kleiner-gleich \(x\), also gleich \(\pi(x)\). Wenn man sich nun vorstellt, dass man die Stufen glättet, so kann man sich vorstellen, wie dadurch die Funktion \( \frac{1}{\ln (t)} \) entsteht. Das folgende Bild zeigt den Vergleich zwischen dieser Stufenfunktion und dem Integranden \( \frac{1}{\ln (t)} \) bis ungefähr 100. Man erkennt, dass die Funktion \( \frac{1}{\ln (t)} \) in diesem Bereich deutlich über der Stufenfunktion liegt. Entsprechend überschätzt \( \mathrm{Li}(x) \) die Funktion \(\pi(x)\) für kleine \(x\), wie wir unten noch sehen werden.
Der Beweis, dass sich \( \mathrm{Li}(x) \) asymptotisch wie \( \frac{x}{\ln (x)} \) und damit auch wie \( \frac{x}{\ln (x) - c} \) verhält, ist nicht allzu kompliziert. Dazu führt man eine partielle Integration im \( \mathrm{Li}(x) \)-Integral durch – die Details überspringen wir hier.
Welche der bisher genannten Funktionen liefert nun die beste Approximation?
Es zeigt sich, dass \( \mathrm{Li}(x) \) am besten abschneidet, denn irgendwann
(d.h. ab einem bestimmten \(x\) ) kommt es immer näher an \(\pi(x)\) heran
als \( \frac{x}{\ln (x) - c} \) , egal welches \(c\) wir verwenden.
Quelle:
Wikimedia Commons File:PrimeNumberTheorem.svg
von Noel Bush, CC BY-SA 3.0
Die folgende Tabelle gibt hierzu einen Überblick:
| \(x\) | \(\pi(x)\) | \( \mathrm{Li}(x) \) | \( \frac{x}{\ln (x) - 1} \) |
|---|---|---|---|
| 1000 | 168 | 178 | 169 |
| 10000 | 1229 | 1246 | 1218 |
| 100000 | 9592 | 9630 | 9512 |
| 1000000 | 78498 | 78628 | 78030 |
| 10000000 | 664579 | 664918 | 661459 |
| 100000000 | 5761455 | 5762209 | 5740304 |
| 1000000000 | 50847534 | 50849235 | 50701542 |
| 10000000000 | 455052511 | 455055614 | 454011971 |
Wie man sieht, ist in der Tabelle stets \( \pi(x) < \mathrm{Li}(x) \) . Dies hatte bereits oben der Vergleich zwischen der Stufenfunktion und dem Integranden \( \frac{1}{\ln (t)} \) von \( \mathrm{Li}(x) \) nahegelegt. Die Verhältnisse ändern sich allerdings für sehr große \(x\) irgendwann, denn Littlewood bewies im Jahr 1914, dass sich die beiden Funktionen \(\pi(x)\) und \( \mathrm{Li}(x) \) unendlich oft schneiden, d.h. mal liegt \(\pi(x)\) oben, mal \( \mathrm{Li}(x) \). Wann allerdings das erste mal \( \mathrm{Li}(x) \) kleiner als \(\pi(x)\) wird, ist unklar. Heute weiß man nur, dass es irgendwann bei sehr großen Zahlen sein muss, aber immerhin unterhalb von \( x = 10^{371} \) geschieht – eine Zahl, die die Anzahl der Atome im sichtbaren Universum weit übertrifft (man schätzt, dass das sichtbare Universum etwa \( 10^{78} \) Atome enthält). Dies ist ein sehr schönes Beispiel dafür, dass ein Verhalten, welches man für sehr viele Zahlen beobachtet, noch lange nicht für alle Zahlen gelten muss. Manchmal geschehen die überaschenden Dinge erst sehr weit draußen!
Um ein Gefühl dafür zu bekommen, was man mit den Approximationen wie \( \frac{x}{\ln (x) - c} \) oder \( \mathrm{Li}(x) \) anfangen kann, möchte ich hier einige bekannte Beispiele nennen:
Wie sieht es mit einem Beweis des Primzahlsatzes aus? Ist es gelungen, zu beweisen, dass sich \( \pi(x) \) für große \(x\) durch Funktionen wie \( \frac{x}{\ln (x)} \) oder \( \frac{x}{\ln (x) - c} \) oder noch besser \( \mathrm{Li}(x) \) approximieren lässt, so dass der relative Fehler für große \(x\) immer kleiner wird? Dabei genügt es, dies für einen der Kandidaten zu beweisen, denn die drei Funktionen approximieren sich ja gegenseitig für große \(x\).
Tatsächlich gelang es im Jahr 1896 den Mathematikern Hadamard und de la Vallée Poussin unabhängig voneinander, den Primzahlsatz zu beweisen. Dabei bauten sie auf Riemanns Arbeit auf, die eine Verbindung zwischen der Primzahlfunktion \(\pi(x)\) und der Zetafunktion \(\zeta(s)\) herstellt. Sie bewiesen, dass der Primzahlsatz äquivalent (gleichwertig) zu der bereits bewiesenen Aussage ist, dass die nichttrivialen Nullstellen der Riemannschen Zetafunktion alle im kritischen Streifen (Realteil von \(s\) zwischen 0 und 1 ohne 0 und 1 selbst) liegen – wir gehen weiter unten noch darauf ein. Beweise ohne die Verwendung der Zetafunktion fanden im Jahr 1949 Atle Selberg und Paul Erdös, ebenfalls unabhängig voneinander. Diese Beweise sind in dem Sinn elementar, dass sie auf die Werkzeuge der komplexen Analysis verzichten und stattdessen mit den elementaren Methoden der Zahlentheorie arbeiten. Diese Beschränkung der Werkzeuge führt jedoch dazu, dass die Beweis selbst sehr kompliziert sind.
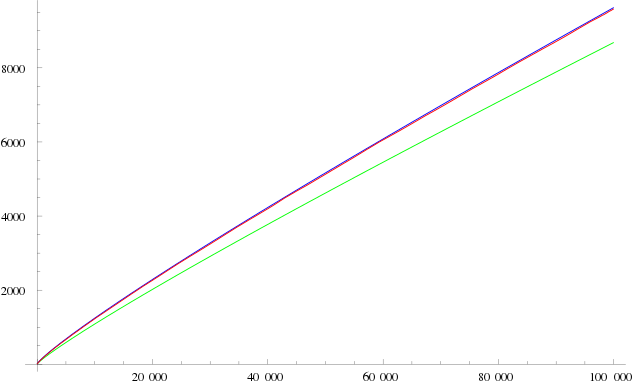
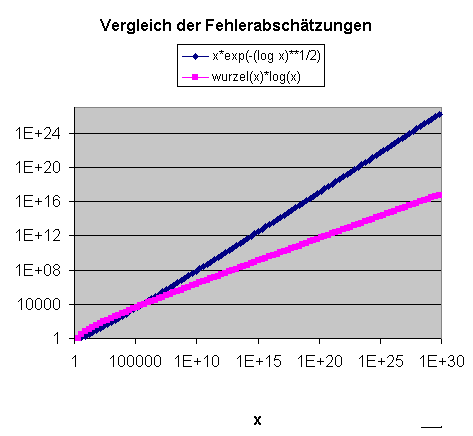
Genau genommen bewiesen Hadamard und de la Vallée Poussin die folgende Fehlerabschätzung: \[ \pi(x) = \mathrm{Li}(x) + O(x \, e^{-a \sqrt{\ln (x)} } ) \] wobei \(a\) eine konstante positive reelle Zahl ist (siehe z.B. Wikipedia: Prime number theorem). Dabei verwenden wir die übliche \(O\)-Notation (auch Landaus \(O\)-Symbol genannt), um das asymptotische Verhalten von Funktionen für große \(x\)-Werte zu charakterisieren:
Hadamard und de la Vallée Poussin bewiesen also, dass die absolute Abweichung \( |\pi(x) - \mathrm{Li}(x)| \) zwischen \(\pi(x)\) und \( \mathrm{Li}(x) \) für genügend große \(x\) kleiner-gleich \( C \, x \, e^{-a \sqrt{\ln (x)} } \) wird, wobei \(C\) und \(a\) geeignete positive Konstanten sind. Eine graphische Darstellung dieser Fehlerabschätzung folgt etwas weiter unten.
Die absolute Abweichung wächst mit ansteigendem \(x\) langsam an. Das ist auch erlaubt. Wichtig ist, dass die relative Abweichung für wachsende \(x\) gegen Null geht. Hadamard und de la Vallée Poussin haben gezeigt, dass das der Fall ist.
Fünf Jahre nach dem Beweis des Primzahlsatzes (also im Jahr 1901) gelang es dem Mathematiker Helge von Koch, eine sehr viel schärfere Abschätzung für die absolute Abweichung \( |\pi(x) - \mathrm{Li}(x)| \) für große \(x\) anzugeben (siehe Wikipedia: Primzahlsatz): \[ \pi(x) = \mathrm{Li}(x) + O( \sqrt{x} \cdot \ln (x) ) \] d.h. es gibt eine reelle Konstante \(C\), so dass \( |\pi(x) - \mathrm{Li}(x)| \leq C \, \sqrt{x} \cdot \ln (x) \) ist, sobald x eine (von \(C\) abhängige) Grenze \(N\) überschreitet. Man kann diese Fehlerabschätzung in guter Näherung folgendermaßen interpretieren (siehe Wolfgang Blum: Chaos hilf! DIE ZEIT 03/2001):
Das passt zu der Tatsache, dass man die Fehlerabschätzung kaum noch nennenswert verbessern kann, denn man weiß, dass \(\pi(x)\) annähernd so stark um \( \mathrm{Li}(x) \) schwankt, wie es die obige Abschätzung angibt.
Nun bewies von Koch die obige Abschätzung jedoch nicht wirklich – sie ist bis heute unbewiesen. Er zeigte vielmehr, dass sie äquivalent zur Riemannschen Vermutung ist. Und damit sind wir beim eigentlichen Thema dieses Kapitels angekommen: der bis heute unbewiesenen Riemannsche Vermutung.
Die folgende Grafik zeigt, welche Verbesserung die neue Fehlerabschätzung
für große Werte von x bedeutet:
Um die Verbindung dieser Fehlerabschätzung zur Riemannschen Vermutung herzustellen, wollen wir uns zunächst eine Funktion ansehen, die eine noch bessere Approximation für die Primzahlverteilung \( \pi(x) \) liefert als dies \( \mathrm{Li}(x) \) bereits tut. Es handelt sich dabei um die sogenannte Riemann-Funktion \(R(x)\), die als eine Summe über die \( \mathrm{Li}(x) \)-Funktion definiert ist:
In der Summe kommen dabei nach dem ersten Term nicht nur negative, sondern auch positive Terme vor. Hier das explizite Bildungsgesetz (siehe Wikipedia: Prime-counting function und Primzahlsatz): \[ R(x) = \sum_{n = 1}^\infty \, \frac{\mu(n)}{n} \, \mathrm{Li}(x^{ \frac{1}{n} }) \] Das Vorkommen und das Vorzeichen des jeweiligen Terms wird dabei durch die Möbius-Funktion \(\mu(n)\) festgelegt, die folgendermaßen für alle natürlichen Zahlen \(n\) definiert ist:
Dazu muss man wissen, dass sich jede natürliche Zahl eindeutig als Produkt von Primzahlen darstellen lässt. Dieses Produkt nennt man auch Primfaktorzerlegung. Man kann die Primzahlen daher auch als die multiplikativen Bausteine (Atome) der natürlichen Zahlen ansehen. So lässt sich beispielsweise die Zahl 20 eindeutig als das Produkt \(2 \cdot 2 \cdot 5\) schreiben. Da die Primzahl 2 doppelt in diesem Produkt vorkommt, ist nach der obigen Definition \( \mu(20) = 0 \).
Die Möbius-Funktion oszilliert wie zufällig zwischen den Werten 1, 0 und -1 hin- und her.
Die ersten Werte dieser Funktion lauten
1,-1, -1, 0, -1, 1, -1, 0, 0, 1, -1, 0, ... .
Die folgende Grafik zeigt die
Möbius-Funktion bis \(n = 50\):
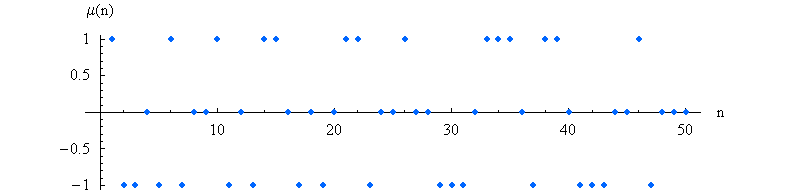
Quelle:
Wikimedia Commons File:MoebiusMu.PNG, Public Domain
Die Riemann-Funktion liefert eine noch bessere Annäherung an \(\pi(x)\) als \( \mathrm{Li}(x) \). Für größere \(x\) liefert die Riemann-Funktion eine Abschätzung, deren Fehler zumeist 5 bis 10 mal kleiner ist als der Fehler bei der \( \mathrm{Li}(x) \)-Funktion.
Es gibt nun einen sehr interessanten exakten
Zusammenhang zwischen der Riemann-Funktion \(R(x)\) und
der Primzahlverteilung \(\pi(x)\)
(siehe Wikipedia: Primzahlsatz;
die Funktion \(\pi_0(x)\) ist praktisch gleich der Funktion \(\pi(x)\), nur an den Sprungstellen
ist sie als Mittelwert zwischen der Stufenhöhe links und rechts definiert):
\[
\pi_0(x) = R(x) - \sum_\rho R(x^\rho) + \]
\[ - \frac{1}{\ln (x)} + \frac{1}{\pi} \arctan \frac{\pi}{\ln (x)}
\]
mit \( x > 1 \).
Dabei geht die Summe über alle sogenannten nicht-trivialen Nullstellen \(\rho\)
der Riemannschen Zetafunktion \(\zeta(s)\) (was das genau bedeutet, sehen wir
uns etwas weiter unten an).
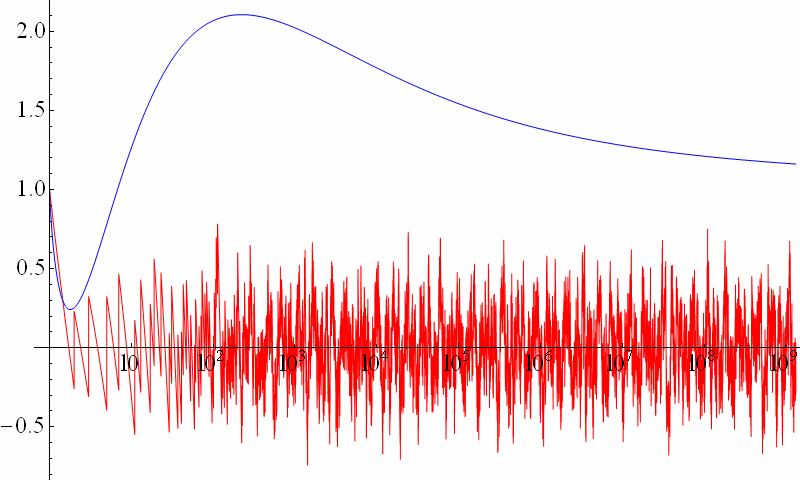
Man kann den Term rechts ohne den Summenterm
\( \sum_\rho R(x^\rho) \)
als bestmögliche glatte Näherung der Primzahlverteilung \( \pi(x) \)
und den Summenterm selbst dann als Fehlerterm oder statistisches Rauschen ansehen.
Dieser Fehlerterm ist dabei durch die Nullstellen einer
gewissen Funktion bestimmt.
Die Riemannsche Vermutung macht nun eine Aussage über
die Lage dieser Nullstellen (Genaueres dazu später) und sagt damit letztlich,
dass sich der Summenterm
tatsächlich wie ein statistischer Störterm verhält,
also gleichsam wie das unvermeidliche Rauschen,
bedingt durch die quasi-zufällige Verteilung der Primzahlen.
Hier ist eine normierte logarithmische Darstellung des Summenterms (rote Kurve):
Schauen wir uns die Riemannsche Zetafunktion \(\zeta(s)\), deren nicht-triviale Nullstellen so interessant sind, etwas genauer an.
Die Riemannsche Zetafunktion dient letztlich dazu, alle vorhandenen Informationen über Primzahlen in einer Weise zu codieren, die diese Informationen für die Anwendung sehr mächtiger mathematischer Werkzeuge zugänglich macht. Es handelt sich dabei um die Werkzeuge der komplexen Analysis (auch Funktionentheorie genannt).
Die Zetafunktion codiert nun die Informationen über Primzahlen und ihre Verteilung auf die folgende Weise: \[ \zeta(s) = \frac{1}{ \left( 1 - \frac{1}{2^s} \right) \cdot \left( 1 - \frac{1}{3^s} \right) \cdot \left( 1 - \frac{1}{5^s} \right) \cdot \cdot \cdot \, } \] d.h. die Zetafunktion ist ein unendliches Produkt von Termen der Form \( \frac{1}{ \left( 1 - p^{-s} \right) } \) , wobei \(p\) alle Primzahlen durchläuft und \(s\) eine reelle Zahl ist mit \(s > 1\) (denn nur dann konvergiert das unendliche Produkt). Man nennt diese Produktdarstellung der Zetafunktion auch Euler-Produkt zu Ehren von Leonhard Euler, der diese Formel im Jahr 1737 bewies (ausgehend von anderen gleichwertigen Definitionen der Zetafunktion, wie wir sie weiter unten noch sehen werden). Abgekürzt lautet die obige Formel: \[ \zeta(s) = \prod_p \frac{1}{ \left( 1 - p^{-s} \right) } \] wobei \( \prod_p \) für ein unendliches Produkt über alle Primzahlen \(p\) steht. Diese Formel gilt wieder für reelle Zahlen \(s > 1\).
Man kann sich relativ leicht überlegen, was passiert, wenn
man das Produkt schrittweise immer weiter ausmultipliziert.
Dazu verwenden wir ein bekanntes Ergebnis über die geometrische Reihe:
\[
1 + q^2 + q^3 + \, ... = \frac{1}{1 - q}
\]
für \( |q| < 1 \).
Also kann jeder Faktor im Euler-Produkt analog zur geometrischen Reihe
als unendliche Summe geschrieben werden:
\begin{align}
& \left( 1 - p^{-s} \right) = \\
& \\
&= 1 + p^{-s} + (p^{-s})^2 + (p^{-s})^3 + \, ... = \\
& \\
&= 1 + \frac{1}{p^s} + \frac{1}{p^{2s}} + \frac{1}{p^{3s}} + \, ...
\end{align}
Es müssen nun im Euler-Produkt unendlich viele dieser geometrischen Reihen miteinander
multipliziert werden, wobei \(p\) in jeder geometrischen Reihe eine andere Primzahl ist.
Das Ergebnis ist eine unendlich lange Summe (eine Reihe) von Termen der
Form 1/(Produkt von Primzahlen)s. Dabei dürfen auch Primzahlen mehrfach
im Primzahlprodukt vorkommen. Eine sorgfältige Buchhaltung zeigt, dass jedes
mögliche Primzahlprodukt genau einmal vorkommt. Nun entspricht aber jedes Primzahlprodukt
in eindeutiger Weise einer natürlichen Zahl, denn das Produkt ist die eindeutige
Primfaktorzerlegung dieser Zahl. Das Ergebnis ist also eine
unendlich lange Summe von Termen der
Form \( 1/n^s \), wobei jede natürliche Zahl \(n\) genau einmal vorkommt.
Damit erhalten wir die bekannteste Darstellung der Zetafunktion:
\[
\zeta(s) = 1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \, ...
\]
oder abgekürzt:
\[
\zeta(s) = \sum_{n = 1}^\infty \, \frac{1}{n^s}
\]
Man kann zeigen, dass diese Reihe für reelle \(s > 1\) konvergiert, also
gegen einen definierten Zahlenwert strebt, wenn man immer mehr Terme aufsummiert.
Für \(s = 1\) dagegen erhält man die divergente
harmonische Reihe,
d.h. die Summe wird hier (wenn auch langsam) immer größer.
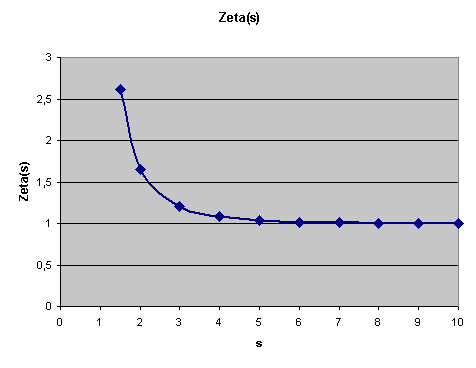
Nun hat man mit dieser Definition der Zetafunktion für reelle Werte von \(s\) oberhalb von 1 noch nicht viel gewonnen. Man könnte hier zwar das gesamte Arsenal der reellen Analysis einsetzen, kommt aber damit noch nicht viel weiter. Von Nullstellen oder anderen interessanten Eigenschaften der Zetafunktion ist hier nichts zu sehen. Spannend wird es erst, wenn wir zu komplexen Zahlen übergehen. Das wollen wir uns nun genauer ansehen.
Innerhalb der reellen Zahlen lassen sich Gleichungen der Form \( x^2 = -1 \) nicht lösen, denn es gibt keine reelle Zahl \(x\), die mit sich selbst multipliziert die negative Zahl \(-1\) ergibt. Man bemerkte jedoch bereits vor einigen hundert Jahren, dass viele Rechnungen einfacher werden, wenn man in den Zwischenschritten so tut, als gäbe es eine solche Zahl – nennen wir sie \(i\). Man kann mit \(i\) wie mit jeder reellen Zahl rechnen. Die einzige Sonderregel lautet: \[ (i)^2 = i \cdot i = -1 \] Nun funktionierten zwar solche Rechnungen mit \(i\) formal einwandfrei, aber keiner wusste, was \(i\) bedeuten sollte. Der Name imaginäre Einheit für \(i\) zeigt dieses Unbehagen (wir sind in Kapitel 3.1 bereits darauf eingegangen). Das Unbehagen verschwand, als Carl Friedrich Gauß und andere eine anschauliche Interpretation von \(i\) und damit der komplexen Zahlen fanden. Wir wollen uns ansehen, was in dieser anschaulichen Interpretation komplexe Zahlen sind.
Betrachten wir eine zweidimensionale Ebene und ein rechtwinkliges Koordinatensystem in dieser Ebene, bestehend aus den üblichen Koordinaten \(x\) und \(y\). In dieser Ebene können wir nun Pfeile einzeichnen, also gerade Linien, die eine bestimmte Länge und eine bestimmte Richtung (gegeben durch die Pfeilspitze) besitzen. Mathematiker sprechen hier auch von zweidimensionalen Vektoren. Man kann jeden dieser Pfeile interpretieren als "gehe \(x\) Schritte nach rechts und \(y\) Schritte nach oben". Ausgehend vom Nullpunkt des Koordinatensystems landet man also durch einen solchen Pfeil an einem Punkt mit den Koordinaten \(x\) und \(y\). Umgekehrt legen \(x\) und \(y\) eindeutig den Pfeil fest (dabei spielt der Anfangspunkt eines Pfeils keine Rolle – wichtig sind alleine Länge und Richtung).
Wir wollen Pfeile (d.h. zweidimensionale Vektoren) mit fetten Buchstaben bezeichnen, z.B. mit \( \boldsymbol{z} \). In karthesischen Koordinaten benutzen wir auch die Schreibweise \[ \boldsymbol{z} = \begin{pmatrix} x \\ y \end{pmatrix} \] Das bedeutet, dass der Pfeil \( \boldsymbol{z} \) aussagt: gehe um \(x\) nach rechts (in Richtung der \(x\)-Achse) und um \(y\) nach oben (in Richtung der \(y\)-Achse). Dabei dürfen \(x\) bzw. \(y\) auch negativ sein, entsprechend einer Bewegung nach links bzw. unten. Die Komonente \(x\) bezeichnet man als Realteil von \( \boldsymbol{z} \), die Komponente \(y\) als Imaginärteil von \( \boldsymbol{z} \). Anstelle von Pfeilen genügt es zu Darstellungszwecken häufig auch, einen Punkt bei den Koordinaten \(x\) und \(y\) einzutragen. Wir wissen dann: gemeint ist ein Pfeil, wie er vom Ursprung \( (0, 0) \) zum Punkt \( (x, y) \) zeigt.
Man kann nun die Addition zweier Pfeile definieren: Zwei Pfeile werden addiert, indem man sie hintereinanderhängt und durch einen neuen Pfeil ersetzt. Statt "gehe \(x_1\) Schritte nach rechts und \(y_1\) Schritte nach oben" und "gehe anschließend \(x_2\) Schritte nach rechts und \(y_2\) Schritte nach oben" sagt die Summe der beiden Pfeile "gehe \(x_1 + x_2\) Schritte nach rechts und \(y_1 + y_2\) Schritte nach oben". Es gilt also:
Die so definierte Pfeiladdition erfüllt alle Regeln, die wir von der Addition reeller Zahlen her gewohnt sind. Beispielsweise kann man die Reihenfolge bei der Addition vertauschen.
Es gibt nun natürlich Pfeile, bei denen immer nur nach rechts (oder links) gegangen wird, aber nie nach oben oder unten. Solche Pfeile haben die Form \[ \boldsymbol{x} = \begin{pmatrix} x \\ 0 \end{pmatrix} \] wobei \(x\) eine reelle Zahl ist und \( \boldsymbol{x} \) einen Pfeil bezeichnet. Addiert man solche Pfeile, so passiert nur in der ersten Koordinate (der \(x\)-Koordinate) etwas. Die \(y\)-Koordinate spielt gar keine Rolle. Eigentlich hätten wir uns für diese Pfeile die \(y\)-Koordinate ganz sparen können. Im Grunde hätten wir gar keine Pfeile gebraucht, denn die Addition dieser Pfeile spiegelt nur die Addition reeller Zahlen wieder. Die Pfeile bringen hier keine neuen Erkenntnisse. Wir können daher sagen:
(natürlich hätten wir stattdessen auch die Hoch-Runter-Pfeile nehmen können, aber irgendwann muss man sich nun einmal entscheiden).
Nun kommt der entscheidende Schritt: Wir wollen neben der Addition auch eine Multiplikation von Pfeilen definieren. Dies tun wir auf die folgende Weise:
Jeder Pfeil besitzt eine Länge und einen Winkel relativ zur x-Achse. Nehmen wir irgendeinen Pfeil \[ \boldsymbol{a} = \begin{pmatrix} x \\ y \end{pmatrix} \] Dann soll \( |\boldsymbol{a}| \) die Länge des Pfeils und \( \varphi_a \) dieser Winkel relativ zur x-Achse sein. Ausgedrückt in karthesischen Koordinaten ist dann nach dem Satz von Pythagoras \[ |\boldsymbol{a}| = \sqrt{x^2 + y^2} \] Den Winkel zur x-Achse kann man mit Hilfe der Winkelfunktionen bestimmen. Umgekehrt ist \( x = |\boldsymbol{a}| \, \cos \varphi_a \) und \( y = |\boldsymbol{a}| \, \sin \varphi_a \), d.h. es ist \[ \boldsymbol{a} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} |\boldsymbol{a}| \, \cos \varphi_a \\ |\boldsymbol{a}| \, \sin \varphi_a \end{pmatrix} \] Man kann \( |\boldsymbol{a}| \) und \( \varphi_a \) als Polarkoordinaten des Pfeils \(\boldsymbol{a}\) ansehen.
Damit sind wir gerüstet für die folgende Definition:
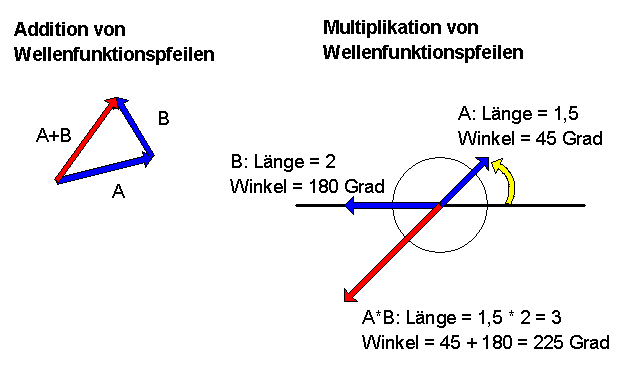
Im Bild werden diese Pfeile als
Wellenfunktionspfeile bezeichnet, die aus der Quantenmechanik stammen
und komplexen Zahlen entsprechen.
Man kann diese Definition, die in Polarkoordinaten (also durch Pfeillänge und Winkel zur \(x\)-Achse) ausgedrückt wurde, auch durch die Koordinaten \(x\) und \(y\) ausdrücken. Eine Rechnung unter Verwendung der Additionstheoreme von Cosinus und Sinus zeigt, dass dann folgender Zusammenhang gilt:
Wieder ist es so, dass für diese Pfeilmultiplikation alle von den reellen Zahlen her gewohnten Rechenregeln gelten. Für Pfeilmultiplikation und Pfeiladdition zusammen gelten ebenfalls alle gewohnten Regeln. Das ist auch der Grund, warum wir weiterhin von Addition und Multiplikation sprechen, obwohl die entsprechenden Definitionen für die Pfeile über das hinausgehen, was wir von den reellen Zahlen her kennen. Allerdings sind die reellen Zahlen und ihre Addition sowie Multiplikation in den Definitionen für Pfeiladdition und Pfeilmultiplikation enthalten. So ist beispielsweise nach der obigen Regel \[ \begin{pmatrix} x_1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ 0 \end{pmatrix} = \begin{pmatrix} x_1 x_2 \\ 0 \end{pmatrix} \] d.h. die Pfeilmultiplikation reproduziert für Rechts-Links-Pfeile wieder die ganz normale Multiplikation reeller Zahlen. Das ist auch anschaulich klar: diese Pfeile liegen ja parallel zur \(x\)-Achse, d.h. ihre Beträge multiplizieren sich und bei den Winkeln ändert sich nichts, denn sie sind Null.
Die obigen Definitionen erweitern den Zahlenbegriff und den Begriff der Addition und Multiplikation, wobei nichts verloren geht. Statt reeller Zahlen verwenden wir Pfeile, die Addition entspricht dem Hintereinanderhängen von Pfeilen (Mathematiker sprechen von Vektoraddition) und die Multiplikation ist eine Drehstreckung, wobei einer der beiden Pfeile um soviel gestreckt und gedreht wird, wie es Betrag und Winkel des anderen Pfeils angeben (wobei die Rollen der beiden Pfeile austauschbar sind). Reelle Zahlen entsprechen dabei Pfeilen, die parallel zur \(x\)-Achse liegen.
Was hat das Ganze nun mit komplexen Zahlen und der Gleichung \[ x^2 = -1 \] zu tun? Nun, innerhalb der reellen Zahlen hat diese Gleichung keine Lösung. Aber was passiert, wenn wir diese Gleichung für Pfeile und deren Multiplikation aufstellen? Statt der reellen Zahl \(x\) müssen wir also einen Pfeil (nennen wir ihn \(\boldsymbol{z}\) ) verwenden, und statt der Zahl \(-1\) den Pfeil \[ - \boldsymbol{1} = \begin{pmatrix} -1 \\ 0 \end{pmatrix} \] der ja der reellen Zahl \(-1\) entspricht (\(\boldsymbol{1}\) ist dabei der Einheitspfeil in \(x\)-Richtung). Die Pfeilgleichung lautet also \[ \boldsymbol{z} \cdot \boldsymbol{z} = - \boldsymbol{1} = \begin{pmatrix} -1 \\ 0 \end{pmatrix} \] Dabei ist der Mal-Punkt \( \cdot \) die Pfeilmultiplikation. Die Frage lautet nun: Ist diese Gleichung für Pfeile und die Pfeilmultiplikation lösbar?
Ja, sie ist es. Es gibt sogar zwei Lösungen, nämlich \[ \boldsymbol{i} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \quad \mathrm{und} \quad -\boldsymbol{i} = \begin{pmatrix} 0 \\ -1 \end{pmatrix} \] Achtung: Noch sind \( \boldsymbol{i} \) und \( -\boldsymbol{i} \) hier einfach Bezeichnungen für spezielle Pfeile. Aber sie ahnen es sicher schon, dass wir die Bezeichnung nicht zufällig so gewählt haben.
Betrachten wir die erste Lösung \( \boldsymbol{i} \): Es handelt sich bei \( \boldsymbol{i} \) um einen Pfeil in \(y\)-Richtung mit Länge 1. Multipliziert man diesen Pfeil mit sich selbst, so ergibt sich also einen Pfeil parallel zur \(x\)-Achse, der nach links zeigt und Länge 1 besitzt: \[ \boldsymbol{i} \cdot \boldsymbol{i} = - \boldsymbol{1} \] Dass das so sein muss, ist auch anschaulich klar, denn \(|\boldsymbol{i}| = 1\) und \(\varphi_i = 90\) Grad. Bildet man \( \boldsymbol{i} \cdot \boldsymbol{i} \) nach unseren Regeln für die Pfeilmultiplikation, so ändert sich am Betrag nichts (denn \(1 \cdot 1 = 1 \)), aber der Winkel verdoppelt sich zu 180 Grad. Die Erweiterung des Zahlbegriffs und des Multiplikationsbegriffs haben die Gleichung \( x^2 = -1 \) lösbar gemacht, wenn man sie als Gleichung für Pfeile und ihre oben definierte Multiplikation versteht.
Es ist keineswegs ungewöhnlich, dass eine Begriffserweiterung zuvor unlösbare Gleichungen lösbar macht! So kannten die Griechen der Antike nur den Begriff der rationalen Zahl (also Brüche). Reelle Zahlen waren unbekannt. Die Gleichung \( x^2 = 2 \) ist aber für rationale Zahlen nicht lösbar. Erst eine entsprechende Erweiterung des Zahlbegriffs (d.h. die Einführung reller Zahlen, z.B. als Grenzwert konvergenter rationaler Zahlenfolgen) konnte dieses Problem lösen.
Nun ist die Pfeilschreibweise \[ \boldsymbol{z} = \begin{pmatrix} x \\ y \end{pmatrix} \] zusammen mit der obigen Multiplikationsregel für Pfeile für Berechnungen ziemlich umständlich. Man kann jedoch die Pfeilschreibweise leicht in eine Schreibweise übersetzen, die analog zum Rechnen mit reellen Zahlen aussieht. Dazu verwenden wir \[ \boldsymbol{z} = \begin{pmatrix} x \\ y \end{pmatrix} = x \, \begin{pmatrix} 1 \\ 0 \end{pmatrix} + y \, \begin{pmatrix} 0 \\ 1 \end{pmatrix} \] Der erste Summand entspricht einfach der reellen Zahl \(x\) mal dem Einheitspfeil \( \boldsymbol{1} \) in \(x\)-Richtung, und der zweite Summand entspricht der reellen Zahl \(y\) mal unserem obigen Pfeil \( \boldsymbol{i} \) in \(y\)-Richtung: \[ \boldsymbol{z} = x \, \boldsymbol{1} + y \, \boldsymbol{i} \]
Das wollen wir vereinfacht wie bei reellen Zahlen schreiben als \[ z = x + i y \] mit der Zusatzregel \[ i \cdot i = -1 \] Den Unterschied zwischen der Pfeilschreibweise und der Zahlen-Schreibweise machen wir dadurch deutlich, dass wir in der Pfeilschreibweise \( \boldsymbol{z} \) oder \( \boldsymbol{i} \) fett schreiben, in der einfacheren Zahlen-Schreibweise dagegen nicht.
Mit \(x, y\) und \(i\) rechnet man nun, als ob sie reelle Zahlen wären (was \(x\) und \(y\) auch sind, nicht aber \(i\) oder \(z = x + i y\)). Auf diese Weise können wir alle oben für Pfeile definierten Regeln leicht reproduzieren:
In der zweiten Formel wurde dabei die Regel \( i \cdot i = -1 \) verwendet. In der Zahlen-Schreibweise spricht man normalerweise nicht mehr von Pfeilen oder Vektoren, sondern von komplexen Zahlen. Es handelt sich aber nur um eine andere Schreibweise! Alles Wesentliche hatten wir bereits oben bei den Pfeilen gesagt, und alle Berechnungen mit komplexen Zahlen können wir auch in der Pfeilschreibweise durchführen, wenn wir wollen. Wir können jederzeit Hin- und Rückübersetzungen zwischen der Pfeilschreibweise und der Zahlen-Schreibweise durchführen!
Es ist sogar oft notwendig, sich auf die Interpretation einer komplexen Zahl durch einen Pfeil zurückzubesinnen, denn Rechnungen mit komplexen Zahlen der Form \(x + i y\) sehen zwar formal so aus wie Rechnungen mit reellen Zahlen, aber ihre Multiplikation hat etwas mit Drehstreckungen von Pfeilen zu tun. Die von reellen Zahlen her gewohnten Anschauungen können daher leicht in die Irre führen.
Man kann nun ganz analog zur reellen Analysis auch für komplexe Zahlen Begriffe wie Funktion, Stetigkeit und Differenzierbarkeit definieren. Diese Definitionen sehen formal genauso aus wie in der reellen Analysis, aber ihre Bedeutung ist sehr viel umfassender.
Beginnen wir mit dem Begriff der Funktion. Für reelle Zahlen ordnet eine Funktion \(f\) jeder reellen Zahl \(x\) eines vorgegebenen Definitionsbereichs jeweils genau eine reelle Zahl \(f(x)\) zu. Reelle Funktionen lassen sich meist gut in einer Graphik veranschaulichen, bei der in einem rechtwinkligen Koordinatensystem Punkte der Form \((x, f(x))\) eingetragen werden. Ein Beispiel haben wir oben bei der Darstellung der Zetafunktion gesehen, die für \(x > 1\) definiert wurde (wobei hier traditionell \(s\) statt \(x\) für die Variable verwendet wird).
Analog geht man bei komplexen Funktionen vor: Eine solche Funktion \(f\) ordnet jeder komplexen Zahl \(z = x + iy\) aus einem bestimmten Definitionsbereich jeweils genau eine komplexe Zahl \[ f(z) = u(z) + i \, v(z) = \] \[ = u(x + iy) + i \, v(x + i y) \] zu. Dabei liefert die reelle Funktion \(u\) die \(x\)-Koordinate des neuen Pfeils (also den Realteil des Funktionswertes), \(v\) dagegen die \(y\)-Koordinate (also den Imaginärteil des Funktionswertes). Beide Funktionen \(u\) und \(v\) hängen dabei von den beiden Koordinaten \(x\) und \(y\) des ursprünglichen Pfeils \(z\) ab. Im Grunde macht die Funktion aus einem zweidimensionalen Pfeil also einen neuen zweidimensionalen Pfeil. Da wir aber für die Pfeile unsere spezielle Multiplikationsregel verwenden wollen, sprechen wir statt von Pfeilen hier von komplexen Zahlen.
Im Grunde kennt man solche Funktionen bereits aus der mehrdimensionalen reellen Analysis, denn eine solche Funktion \(f\) macht aus einem zweidimensionalen reellen Vektor (Pfeil) einen neuen zweidimensionalen reellen Vektor.
Wie kann man sich nun solche Funktionen veranschaulichen?
Leider scheidet ein einfacher Graph wie bei den reellen Funktionen \(f(x)\) aus, denn jeder Punkt in einem solchen Graph hätte 4 Koordinaten (nämlich \(x, y, u, v\) ). Der Graph einer solchen Funktion wäre also eine Punktemenge in einem vierdimensionalen Raum und ist damit unserer Anschauung nicht zugänglich.
Es gibt jedoch andere Methoden. Eine Möglichkeit besteht darin, die Funktion \(f\) als Vektorfeld in der zweidimensionalen Ebene darzustellen. Dazu zeichnet man einfach an verschiedenen Punkten \((x, y)\) einen Pfeil ein, dessen Länge und Richtung den Funktionswert \(f(x,y)\) an dieser Stelle darstellt. Damit ergibt sich so etwas wie ein zweidimensionales Strömungsfeld. Man kann sich z.B. vorstellen, dass die Pfeile die Fließgeschwindigkeit und Fließrichtung einer Flüssigkeit in einem flachen Becken darstellen. Besonders interessant sind dabei zwei Eigenschaften dieses Strömungsfeldes: Wirbel, also kreisförmige Bewegungen, und Quellen sowie Senken für die Flüssigkeit. Mathematisch drückt man diese beiden Eigenschaften durch die Rotation und die Divergenz des Vektorfeldes aus. Wir kommen weiter unten noch genauer darauf zurück.
Problematisch wird diese Darstellung dann, wenn die Pfeillängen sehr unterschiedlich sind oder wenn man nicht genug Pfeile einzeichnen kann, um interessante Details der Funktion darzustellen. Außerdem gibt es bestimmte Eigenschaften von Funktionen, die man in Vektorfeldern nicht gut erkennen kann. Dann ist eine andere Darstellungsart sehr nützlich: Man zeichnet in einem ersten Bild bestimmte Linien in die \(x\)-\(y\)-Ebene ein, z.B. ein rechtwinkliges Gitternetz, das die karthesischen Koordinaten \(x\) und \(y\) darstellt, oder ein radiales Spinnennetz, das die Ebene mit einem Polarkoordinatennetz überzieht. In einem zweiten Bild zeichnet man nun ein, wo die Punkte der Linien in der \(x\)-\(y\)-Ebene landen, wenn man \(f(x,y)\) auf sie anwendet. Auf diese Weise kann man sehr schön die Verzerrungen und Verdrehungen sehen, die \(f\) verursacht. Problematisch wird es allerdings, wenn \(f\) mehrere verschiedene Punkte \((x,y)\) auf die gleichen Bildpunkte \((u,v)\) abbildet. In diesem Fall sollte man sich Teilbereiche der Ebene herausgreifen und nur deren Abbildung unter \(f\) betrachten. Wir werden unten noch Beispiele für diese Darstellungsweise sehen.
Natürlich gibt es noch weitere Möglichkeiten. Man kann z.B. in der \(x\)-\(y\)-Ebene dort Linien einzeichnen, wo \(u = 0 \) ist bzw. wo \(v = 0\) ist. Die Linien \( u(x+iy) = 0 \) bedeuten für das entsprechende Vektorfeld, dass die Pfeile dort senkrecht liegen. Analog bedeutet \( v(x+iy) = 0 \), dass die Pfeile dort waagrecht liegen. Wir werden weiter unten diese Darstellungsform für die Zetafunktion noch nutzen.
Schließlich kann man noch \(|f(x+iy)|\) oder \(u(x+iy)\) oder \(v(x+iy)\) als Gebirge über der \(x\)-\(y\)-Ebene darstellen. Diese Darstellung verschleiert jedoch viele interessante Eigenschaften von \(f\) und ist hauptsächlich dazu nützlich, um z.B. Pole oder Nullstellen leicht zu sehen.
Man kann nun schrittweise alle Begriffe der reellen Analysis auf die komplexe Analysis übertragen. So kann man definieren, wann eine Funktion \(f(z)\), die komplexe Zahlen auf komplexe Zahlen abbildet, stetig (also "glatt") ist. Die Details wollen wir hier überspringen, denn viel wichtiger ist der Begriff der komplexen Ableitung:
Bei reellen Funktionen definiert man den Begriff der Ableitung \(f'\) einer Funktion \(f\) in einem Punkt \(x\) als die Steigung der Tangente, die man an den Graphen dieser Funktion dort anlegen kann. In Formeln ausgedrückt ist diese Steigung gleich dem Grenzwert \[ f '(x) = \lim_{h \rightarrow 0} \, \frac{f(x+h) - f(x)}{h} \] Gleichwertig dazu ist die Aussage, dass in der Nähe von \(x\) der Funktionswert \(f(x+h)\) durch die Tangente in \(x\) angenähert werden kann: \[ f(x+h) = f(x) + f '(x) \cdot h + r(x,h) \] mit \[ \lim_{h \rightarrow 0} \, \frac{r(x,h)}{h} = 0 \] Wir können die Gleichung \( f(x+h) = f(x) + f '(x) \cdot h + r(x,h) \) nämlich leicht nach \(f'(x)\) freistellen mit dem Ergebnis \[ f'(x) = \frac{f(x+h) - f(x)}{h} + \frac{r(x,h)}{h} \] Wenn wir hier den Grenzwert von \(h\) gegen Null bilden, fällt \( \frac{r(x,h)}{h} \) weg und wir erhalten die Formel weiter oben.
Die Abweichung \(r(x,h)\) von der Tangente \( f(x) + f '(x) \cdot h \) muss also schneller als \(h\) klein werden, wenn \(h\) gegen Null strebt. Beispielsweise könnte \(r(x,h) = h^2 \) sein. Das bewirkt, dass \(r(x,h)\) für kleine \(h\) gegenüber \( f '(x) \cdot h \) nicht mehr ins Gewicht fällt (vorausgesetzt, \(f '(x)\) ist ungleich Null). Diese Darstellung hat den Vorteil, dass man sie auf mehrdimensionale reelle Funktionen übertragen kann, bei denen sich ein Bruch wie \( \frac{f(x+h) - f(x)}{h} \) nicht immer gut definieren lässt.
Wenn das oben definierte \(f '(x)\) existiert, so ist \(f\) ableitbar oder differenzierbar im Punkt \(x\), d.h. man kann dort eine eindeutige Tangente anlegen. Dies geht nicht, wenn \(f\) in \(x\) einen Knick hat wie z.B. die Funktion \(f(x) = |x|\) in \(x = 0\). Differenzierbarkeit bedeutet bei reellen Funktionen also, dass der Funktionsgraph so glatt ist, dass sich eine Tangente anlegen lässt. Nur wenn \(f\) in \(x\) differenzierbar ist, gilt die obige Formel \( f(x+h) = f(x) + f '(x) \cdot h + r(x,h) \) mit \( \lim_{h \rightarrow 0} \, \frac{r(x,h)}{h} = 0 \).
Man kann nun einfach die obige Definition der Ableitung vollkommen unverändert auf komplexe Zahlen übertragen, wobei man üblicherweise \(z\) statt \(x\) schreibt, um klarzumachen, dass es sich um eine komplexe Zahl handelt. Aber nicht nur \(z\), sondern alle Objekte sind dann komplexe Zahlen und es gelten die Regeln für die Multiplikation komplexer Zahlen. Der Limes von \(h\) gegen Null ist hierbei so zu verstehen, dass \(h\) einen beliebigen Winkel zur \(x\)-Achse aufweisen darf. Man darf sich also aus beliebiger Richtung in der zweidimensionalen Ebene der komplexen Zahlen dem Punkt \(z\) nähern. Der Grenzwert existiert nur dann, wenn er für jede dieser Richtungen dieselbe komplexe Zahl \(f '(z)\) liefert. Nur dann ist \(f\) in \(z\) komplex differenzierbar (ableitbar)! Daran sehen wir schon, dass ein neuer Aspekt hinzukommt, den es bei reellen Zahlen noch nicht gab, auch wenn alle Formeln vollkommen gleich aussehen.
Wir haben also \[ f '(z) = \lim_{h \rightarrow 0} \, \frac{f(z+h) - f(z)}{h} \] Die Division durch die komplexe Zahl \(h\) ist dabei leicht zu verstehen. So haben wir für den Kehrwert von \(z=x+iy\) den Ausdruck \[ \frac{1}{z} = \frac{1}{x+iy} = \frac{x-iy}{(x-iy) \, (x+iy)} = \] \[ = \frac{x-iy}{(x^2 + y^2)} = \frac{z^*}{|z|^2} \] mit dem komplex konjugierten \( z^* := x-iy \). Analog für die Division durch \(h\).
Nun ist die Division durch die komplexe Zahl \(h\) manchmal etwas unhandlich. Schauen wir uns daher die zweite Formulierung genauer an: \[ f(z+h) = f(z) + f '(z) \cdot h + r(z,h) \] mit \( \lim_{h \rightarrow 0} \, \frac{r(z,h)}{h} = 0 \). Hier sieht man sehr schön, dass die Multiplikation zwischen den komplexen Zahlen \(f'(z)\) und \(h\) eine wichtige Rolle spielt. Aber was bedeutet nun diese Definition der komplexen Ableitung anschaulich?
Zunächst einmal hat sie nichts mehr mit der Tangente an einem Graphen zu tun, wie das bei reellen Zahlen noch der Fall war. Der Term \(f'(z) \cdot h\) entspricht nicht mehr (wie im reellen Fall) dem Anstieg einer Geraden, wenn man sich um den kleinen Schritt \(h\) von \(x\) wegbewegt. Was er statt dessen bedeutet, versteht man besonders gut, wenn man wieder die Pfeil-Interpretation der komplexen Zahlen heranzieht. Dabei wird der Pfeil \(h\) einer Drehstreckung unterworfen, die durch den Pfeil \(f'(z)\) festhelegt wird – wir erinnern uns: Pfeillängen werden multipliziert und Pfeilwinkel (zur \(x\)-Achse) werden addiert. Die Pfeillänge \(|h|\) wird also mit \(|f'(z)|\) multipliziert, und der Winkel \( \varphi_h \) von \(h\) wird um den Winkel \( \varphi_{f'(z)} \) vergrößert.
Wir wollen die Schreibweise etwas vereinfachen und \[ \varphi_{f'(z)} =: \theta \] schreiben, d.h. \[ f '(z) = |f '(z)| \, ( \cos \theta + i \sin \theta ) \] Weiterhin haben wir \(f(z) = u(z) + i \, v(z) \) mit \( z = x + iy \) und \( h = h_x + i h_y \) sowie \(r = r_x + i \, r_y\) (die Argumente \( (z,h )\) lassen wir bei der Restfunktion \(r\) zur Vereinfachung weg). In Komponenten ausgeschrieben lautet dann die obige Gleichung: \begin{align} f(z+h) &= u(z+h) + i \, v(z+h) = \\ & \\ & = f(z) + f '(z) \cdot h + r = \\ & \\ &= u(z) + i \, v(z) + \\ &+ |f '(z)| \, ( \cos \theta + i \sin \theta ) \, (h_x + i h_y) + \\ & + r_x + i \, r_y = \\ & \\ &= u(z) + i \, v(z) + \\ &+ |f '(z)| \, ( h_x \, \cos \theta - h_y \, \sin \theta + \\ & \quad \quad \quad + i h_x \, \sin \theta + i h_y \, \cos \theta ) + \\ & + r_x + i \, r_y \end{align} und somit für Real- und Imaginärteil (also \(x\)- und \(y\)-Pfeilkomponente) getrennt: \begin{align} u(z+h) &= u(z) + |f '(z)| \, ( h_x \, \cos \theta - h_y \, \sin \theta ) + r_x \\ v(z+h) &= v(z) + |f '(z)| \, ( h_x \, \sin \theta + h_y \, \cos \theta ) + r_y \end{align} Man erkennt hier sehr schön, wie der Pfeil \(h\) um den Winkel \(\theta\) gegen den Uhrzeigersinn gedreht und um \(|f '(z)|\) gestreckt bzw. gestaucht wird.
Es ist an dieser Stelle interessant, dieses Ergebnis mit dem zweidimensionalen reellen Fall zu vergleichen. Dort ist eine Funktion \(f = (u, v) \) in \(z = (x, y) \) differenzierbar, wenn man sie bei \(z\) durch eine lineare Abbildung approximieren kann: \begin{align} u(z+h) &= u(z) + ( h_x \, \frac{\partial u}{\partial x} + h_y \frac{\partial u}{\partial y} ) + r_x \\ v(z+h) &= v(z) + ( h_x \, \frac{\partial v}{\partial x} + h_y \frac{\partial v}{\partial y} ) + r_y \end{align} (die Fettschreibung für zweidimensionale Vektoren sparen wir uns hier, analog zur Zahlenschreibweise komplexer Zahlen). Dabei ist z.B. \(\frac{\partial u}{\partial x}\) die partielle Ableitung von \(u\) nach der Variable \(x\) (ausgewertet am Punkt \(z = (x,y) \)). Diese Ableitung kann eine beliebige reelle Zahl sein!
Der zweidimensionale reelle Fall ist viel allgemeiner als der Fall der komplexen Ableitung. Der Pfeil \(h\) kann hier einer beliebigen linearen Abbildung unterworfen werden, die durch die partiellen Ableitungen von \(u\) und \(v\) gegeben ist. Bei der komplexen Ableitbarkeit dagegen fordert man, dass diese lineare Abbildung eine Drehstreckung sein muss. Bei der komplexen Ableitung muss also \begin{align} \frac{\partial u}{\partial x} &= \;\;\; |f '(z)| \, \cos \theta \\ \frac{\partial u}{\partial y} &= - |f '(z)| \, \sin \theta \\ \frac{\partial v}{\partial x} &= \;\;\; |f '(z)| \, \sin \theta \\ \frac{\partial v}{\partial y} &= \;\;\; |f '(z)| \, \cos \theta \end{align} gelten. Wie wir sehen, sind die rechten Seiten in den Gleichungen 1 und 4 gleich sowie in 2 und 3 negativ-gleich, d.h. bei komplex differenzierbaren Funktionen muss für die partiellen Ableitungen gelten:
Daher ist die Forderung, dass \(f\) komplex ableitbar sein soll, sehr viel strenger als die Forderung, dass \(f\) zweidimensional-reell ableitbar sein soll. Sehr viele zweidimensional-reell-differenzierbare Funktionen \(f\) fallen weg, wenn wir die Forderung nach komplexer Ableitbarkeit erheben. Funktionen, die komplex ableitbar (differenzierbar) sind, weisen daher ganz spezielle Eigenschaften auf!
Schauen wir uns eine dieser Eigenschaften an: Nehmen wir an, wir bewegen uns im Abstand \( |h| \) in einem sehr kleinen Kreis um einen fest vorgegebenen Punkt \(z\) herum, d.h. die Länge des kurzen Pfeils \(h\) liegt fest, aber sein Winkel \( \varphi_h \) ändert sich. Dabei soll die Länge von \(h\) so klein sein, dass die Restfunktion \(r(z,h)\) keine Rolle spielt und wir sie in guter Näherung weglassen können ( \(f'(z) \) ungleich Null sei vorausgesetzt). Wie verändert sich nun der Funktionswert \(f(z+h)\) bei unserer Kreiswanderung um den festen Punkt \(z\) herum?
Die Pfeilspitze von \(f(z+h)\)
ergibt sich aus der Pfeilspitze von \(f(z)\),
indem wir den kleinen Pfeil \(f'(z) \cdot h\) hinzuaddieren.
Nun beschreibt die komplexe Multiplikation
mit \(f'(z)\) eine feste Drehstreckung, die jedes \(h\)
in gleicher Weise verändert: Streckung um einen bestimmten Faktor und Drehung
um einen bestimmten Winkel. Wenn sich nun \(h\) im Kreis dreht,
so tut dies auch sein drehgestrecktes Gegenstück \(f'(z) \cdot h\),
und zwar mit derselben Winkelgeschwindigkeit im gleichen Drehsinn.
Daher dreht sich die Pfeilspitze von \(f(z+h)\)
im Gleichklang mit \(h\) um die Pfeilspitze von \(f(z)\).
Hier ein Beispiel:
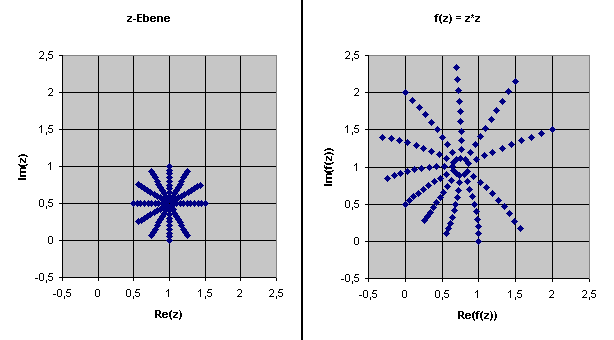
Der Mittelpunkt dieses neuen Gitternetzes rechts liegt bei
\( f(1 + i/2) = (3/4 + i)\).
Je näher man sich an diesem Mittelpunkt befindet, umso kreisförmiger werden die Ringe des
Gitternetzes. Die Ringe nahe am Mittelpunkt sind in guter Näherung durch die Formel
\(f(z+h) = f(z) + f'(z) \cdot h \) gegeben.
Erst weiter weg weichen die Ringe deutlich von der Kreisform ab, da
dann der Restterm \(r(z,h)\) nicht mehr vernachlässigbar ist.
Im allgemeinen Fall einer zweidimensional-reell-differenzierbare Funktionen \(f\) muss das nicht so sein. Hier bewegt sich die Pfeilspitze von \(f(z+h)\) auf einer Ellipse um die Pfeilspitze von \(f(z)\) (denn eine lineare Abbildung macht aus einem Kreis eine Ellipse). Bei einer komplex differenzierbaren Funktion \(f\) muss es dagegen ein Kreis sein!
Dadurch ergibt sich eine sehr interessante Eigenschaft komplex differenzierbarer Funktionen: Wir markieren zwei Punkte auf dem kleinen Kreis, der durch die Drehung von \(z+h\) um \(z\) entsteht, d.h. wir wählen zwei spezielle Pfeile \(h_1\) und \(h_2\) aus. Den Winkel zwischen diesen zwei Pfeilen nennen wir \(\alpha\). Nun wenden wir die Funktion \(f\) an. Aus dem Kreis entsteht für kleine \(|h|\) in guter Näherung ein neuer Kreis, der durch die Punkte (Pfeilspitzen) von \( f(z+h) = f(z) + f'(z) \cdot h \) gegeben ist. Auch die Abbilder der beiden markierten Punkte finden wir hier wieder. Sie entstehen, indem wir zu \(f(z)\) (dem Kreismittelpunkt) den Pfeil \(f'(z) \cdot h_1\) bzw. den Pfeil \(f'(z) \cdot h_2\) hinzuaddieren. Der Winkel zwischen diesen beiden Pfeilen ist derselbe wie der Winkel \(\alpha\) zwischen \(h_1\) und \(h_2\), denn beide Pfeile werden um die gleiche Drehstreckung \(f'(z)\) verändert. Man sagt, die Abbildung \(f\) ist winkeltreu oder konform:
Diese Eigenschaft sieht man besonders gut in der Gitternetzdarstellung analog zu der Abbildung oben.
Wir erinnern uns:
Man überzieht in einem ersten Bild die zweidimensionale Ebene mit einem Gitternetz
(diesmal allerdings ein rechtwinkliges und kein radiales Gitternetz).
In einem zweiten Bild zeichnet man nun ein, wo die Punkte der Gitternetzlinien landen,
wenn man \(f\) auf sie anwendet. Die Konformität (Winkeltreue) von \(f\) sieht man nun daran,
dass sich im zweiten Bild die Gitternetzlinien in jedem Schnittpunkt unter demselben Winkel
schneiden wie im dazugehörenden Schnittpunkt des ersten Bildes. Ein rechtwinkliges Gitter
wird wieder zu einem rechtwinkligen Gitter, wobei aber aus geraden Linien durchaus krumme Linien
werden dürfen. Die folgende Grafik zeigt dies wieder am Beispiel \(f(z) = z^2\).
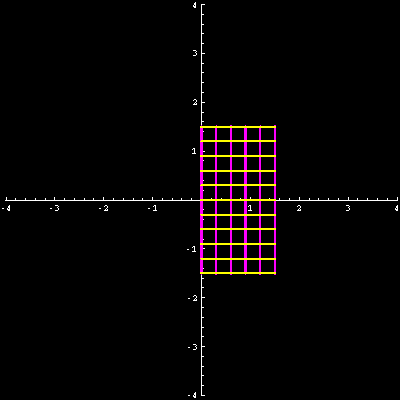
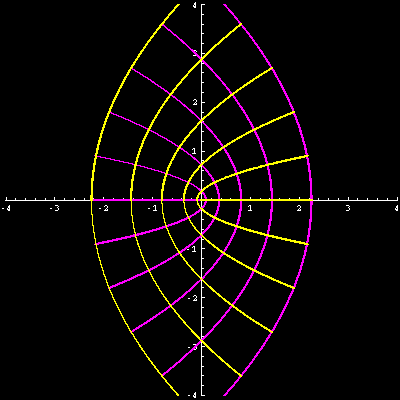
Quelle:
Douglas N. Arnold, GRAPHICS FOR COMPLEX ANALYSIS,
dort veröffentlicht unter der
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License.
Auf der Webseite von Douglas N. Arnold
findet man noch viele weitere Bilder zu komplex differenzierbaren
Funktionen.
Auch in anderen Darstellungen sieht man die Besonderheiten komplex differenzierbarer Funktionen. Wir hatten oben die Darstellung als Vektorfeld erwähnt: Dazu zeichnet man einfach an verschiedenen Punkten \(z\) einen Pfeil ein, dessen Länge und Richtung \(f(z)\) darstellt. Es stellt sich jedoch heraus, dass es günstiger ist, statt dem Pfeil \(f(z)=u(z)+iv(z)\) den komplex-konjugierten Pfeil \(f^*(z)=u(z)-iv(z)\) einzuzeichnen. Das entsprechende Vektorfeld bezeichnet man auch als Polya-Vektorfeld (Bilder siehe z.B. Resources for Teaching Complex Variables, insbesondere Polya Vector Fields).
Das Polya-Vektorfeld hat zwei sehr schöne Eigenschaften: Überall da, wo \(f\) definiert ist und komplex differenzierbar ist, ist das Polya-Vektorfeld quellenfrei und wirbelfrei. Interpretiert man das Polya-Vektorfeld als Strömungsfeld einer Flüssigkeit, so bedeutet dies, dass es keine Quellen oder Senken sowie keine Wirbel für die Flüssigkeit gibt, außer an den Stellen, wo \(f\) nicht definiert oder nicht komplex differenzierbar ist (z.B. an Polstellen). Mathematisch ist dies eine Folge der oben erwähnten Cauchy-Riemannschen Differentialgleichungen: \begin{align} \mathrm{div} \, f^*(z) &= \; \; \; \frac{\partial u}{\partial x} - \frac{\partial v}{\partial y} = 0 \\ \mathrm{rot} \, f^*(z) &= - \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} = 0 \\ \end{align}
(genau genommen muss man dabei die Pfeile als dreidimensionale Vektoren ansehen mit \(z\)-Komponente gleich Null).
Besonders interessant wird es nun, wenn man Wegintegrale komplex differenzierbarer Funktionen für geschlossene Wege betrachtet. Die Quellenfreiheit und Wirbelfreiheit bewirkt, dass man viele dieser Integrale explizit ausrechnen kann, und dass ihr Wert zumeist nicht vom konkreten Weg abhängt, sondern von der Natur der Pole im umschlossenen Gebiet. Das liegt daran, dass sich ein Pol wie eine Quelle oder Senke für das Polya-Vektorfeld auswirkt. In der Polya-Vektorfelddarstellung kann man auch leicht die Ordnung (Vielfachheit) eines Pols oder einer Nullstelle sehen. Dazu zählt man einfach, wie oft sich das Vektorfeld dreht, wenn man einmal um den Pol bzw. die Nullstelle herumläuft. Nähere Details dazu findet man z.B. in Polya Vector Fields und Jackie Burm and Amanda Peterson: Interpretation of the Complex Contour Integral (1998).
Was hat das Ganze nun mit der Riemannschen Zetafunktion zu tun?
Die Idee ist folgende: Bisher war unsere Zetafunktion \( \zeta(s) \) nur für reelle Variablenwerte \( s \) definiert, und ihre Funktionswerte waren ebenfalls reell. Können wir daraus eine komplexe differenzierbare Funktion machen, also eine Funktion \( \zeta(z) \), die für reelle \(z\)-Werte genau unsere reelle Funktion ergibt?
Man nennt eine solche Funktion \( \zeta(z) \) die analytische Fortsetzung von \( \zeta(s) \). Generell kann man zu jeder reellen Funktion \(f(x)\), die für \(x\) einem reellen Intervall definiert ist, genau eine analytische Fortsetzung \(f(z)\) finden, die auf einem Gebiet komplexer Zahlen definiert ist, das das reelle Intervall enthält. Diese analytische Fortsetzung ist eindeutig. Voraussetzung ist, dass \(f\) hinreichend gutartig ist. Das bedeutet genauer: \(f\) muss reell analytisch sein, sich also im reellen Intervall in eine konvergente Potenzreihe entwickeln lassen. Das ist bei der Zetafunktion der Fall.
Schreibt man \(f(z) = u(z) + i v(z)\) sowie \(z = x + i y\), so muss demnach \(v(x) = 0\) und \(u(x) = f(x)\) sein, damit die komplexe Funktion auf der reellen Achse gerade gleich der reellen Funktion ist. Die Funktion \(f(z)\) bildet also Punkte der reellen \(x\)-Achse wieder auf Punkte der reellen \(x\)-Achse ab.
Für die Zetafunktion wird aus historischen Gründen auch für komplexe Variablenwerte meist der Buchstabe \(s\) statt \(z\) verwendet, d.h. wir schreiben im Folgenden \(\zeta(s)\), wobei \(s = x + i y\) ist, und \(\zeta(s)\) die analytische Fortsetzung der reellen Zetafunktion ist.
Wie erhält man nun die analytische Fortsetzung einer reellen Funktion? Schauen wir uns dazu zunächst einige Beispiele an:
Die analytische Fortsetzung der Funktion \(f(x) = x^n\) mit einer vorgegebenen natürlichen Zahl \(n\) ist einfach \(f(z) = z^n\) , d.h. das reelle Argument \(x\) wird durch das komplexe Argument \(z\) ersetzt. Gemeint ist, dass \(z\) n-mal mit sich selbst im Sinne der komplexen Multiplikation (Pfeilmultiplikation) multipliziert wird. Für \(n = 2\) haben wir oben eine grafische Darstellung dieser Funktion gesehen. Die Funktion \(f(z) = z^n\) ist überall komplex differenzierbar, denn analog zu der reellen Funktion folgt aus der Definition der komplexen Ableitung: \(f'(z) = n \, z^{n-1} \) .
Analog ist es auch bei der Funktion \(f(x) = 1/x\) . Die analytische Fortsetzung lautet \(f(z) = 1/z \) (was das bedeutet, haben wir weiter oben bereits gesehen).
Eine sehr wichtige Funktion ist die Exponentialfunktion oder auch \(e\)-Funktion \(f(x) = e^x\) , oft auch als \(f(x) = \exp(x)\) geschrieben. Dabei ist \(e\) = 2,71828 18284 59045 23536 02874 ... . Die \(e\)-Funktion hat einige wichtige Eigenschaften. So ist die Ableitung dieser Funktion gleich der Funktion selbst: \[ \frac{d e^x}{dx} = e^x \] und es gilt die Regel \[ e^{x+y} = e^x \cdot e^y \] Weiterhin kann man eine einfache, überall konvergente Reihenentwicklung angeben: \[ e^x = 1 + x + \frac{1}{2} x^2 + \frac{1}{3 \cdot 2} x^3 + \, ... \] Die analytische Fortsetzung der \(e\)-Funktion erhält man, indem man in dieser Reihenentwicklung das reelle \(x\) durch das komplexe \(z\) ersetzt. Alle oben genannten Regeln gelten dann auch für \(f(z) = e^z\).
Mit Hilfe der Reihenentwicklungen der Winkelfunktionen Sinus und Cosinus kann man eine der wichtigsten Formeln in der Theorie komplexer Funktionen beweisen. Es gilt: \[ e^{i \varphi} = \cos \varphi + i \, \sin \varphi \] mit reellem \(\varphi\). Die komplexe Zahl \(e^{i \varphi}\) entspricht also einem um den Winkel \(\varphi\) (angegeben im Bogenmaß} nach links gedrehten Pfeil der Länge Eins. Multipliziert man irgendeine komplexe Zahl mit \(e^{i \varphi}\), so wird der entsprechende Pfeil einfach um den Winkel \(\varphi\) nach links gedreht, d.h. die Multiplikation mit \(e^{i \varphi}\) entspricht einer Drehung um den Winkel \(\varphi\) nach links.
Damit lässt sich jede kompleze Zahl \(z\) schreiben als \[ z = |z| \, e^{i \varphi} \] wobei \(|z|\) die Länge des Pfeils ist und \(\varphi\) der Winkel des Pfeils zur \(x\)-Achse.
Weiterhin gilt für die Funktion \( f(z) = e^z \) mit komplexem \(z=x+iy\) die Formel: \[ e^z = e^{x+iy} = e^x \, e^{iy} = e^x \, (\cos y + i \, \sin y) \] Als Pfeil dargestellt besitzt \(e^z\) also die Länge \(e^x\) und den Winkel \(y\) zur \(x\)-Achse. Wir werden diese Formel etwas weiter unten für die Zetafunktion noch benötigen.
Um zu verstehen, was der Begriff analytische Fortsetzung wirklich bedeutet, ist es hilfreich, eine anschauliche Vorstellung dieses Begriffs zu entwickeln. Dies kann man auf verschiedene Weise tun. Wir wollen uns hier zwei Möglichkeiten anschauen, die beide ihre eigenen Vor- und Nachteile haben:
Die erste Möglichkeit verwendet die Darstellung komplex differenzierbarer Funktionen \(f(z) = u(z) + i v(z)\) durch das Polya-Vektorfeld \(f^*(z) = u(z) - i v(z)\) (siehe oben). Man beginnt damit, das Polya-Vektorfeld der reellen Funktion \(f(x)\) in einem x-y-Koordinatensystem einzuzeichnen. Das ist sehr einfach: an jedem Punkt \(x\) des Definitionsbereichs von \(f\) auf der reellen \(x\)-Achse zeichnet man den waagerechten Pfeil mit Länge \(f(x)\) ein – er liegt parallel zur \(x\)-Achse und repräsentiert den reellen Funktionswert. In der Praxis wird man die Pfeile natürlich nur für einige ausgewählte \(x\)-Werte einzeichnen.
Die Aufgabe lautet nun: zeichne auch oberhalb und unterhalb der \(x\)-Achse Pfeile ein, und zwar so, dass das so entstehende Vektorfeld keine Wirbel und keine Quellen oder Senken aufweist, soweit das möglich ist. Dabei kann man sich vorstellen, wie man sich Schritt für Schritt von der \(x\)-Achse her nach oben und unten vortastet und die neuen Pfeile immer so anbringt, dass Quellen und Senken sowie Wirbel vermieden werden. Man kann zeigen, dass es immer nur eine eindeutige Möglichkeit gibt, die Pfeile entsprechend einzutragen.
Auf diese Weise versucht man, möglichst große Gebiete der komplexen Ebene mit Pfeilen zu überdecken. In vielen Fällen wird man ohne Probleme die gesamte Ebene so mit Pfeilen versehen können und dabei vielleicht sogar Gebiete der \(x\)-Achse erreichen, auf denen \(f\) vorher gar nicht definiert war (wir kommen weiter unten noch einmal darauf zurück). Es kann aber auch Punkte geben, an denen sich kein Pfeil konsistent eintragen lässt. An diesen Punkten ist die analytische Fortsetzung dann nicht definiert. Für solche Punkte ist es auch erlaubt, dass sie z.B. wie Quellen oder Senken wirken. Typischerweise hat die analytische Fortsetzung an diesen Stellen sogenannte Pole (so wie beispielsweise die Funktion \(f(z) = 1/z\) bei \(z = 0\) eine Pol hat).
Das so entstehende Polya-Vektorfeld \(f^*(z)\) können wir am Schluss wieder in eine komplex differenzierbare Funktion \(f(z)\) zurückübersetzen. Diese Funktion ist dann die analytische Fortsetzung der reellen Funktion \(f(x)\).
Und nun zur zweiten Möglichkeit, bei der wir statt der Vektorfelddarstellung die Gitternetzdarstellung verwenden. Wir überziehen also einen Teil der komplexen \(z\)-Ebene, der den reellen Definitionsbereich von \(f\) enthält, mit einem Gitternetz (z.B. einem rechtwinkligen x-y-Gitter) und fragen uns, wo die Gitterpunkte landen, wenn wir aus jedem Punkt \(z\) den Punkt \(f(z)\) machen.
Für die Punkte der reellen \(x\)-Achse, die im Definitionsbereich von \(f\) liegen, ist das wieder sehr einfach: jeder Gitternetzunkt \((x, 0)\) landet beim entsprechenden Punkt \((f(x), 0)\).
Und nun tasten wir uns wieder in den Bereich oberhalb und unterhalb der \(x\)-Achse vor: Das Gitternetz muss nach oben und unten so ergänzt werden, dass die Schnittwinkel zwischen den Gitternetzlinien dieselben sind wie vorher, denn komplex differenzierbare Funktionen sind konform (winkelerhaltend). Dies muss für beliebige Gitternetze gelten! Das Ergebnis ist, dass es nur eine einzige Möglichkeit gibt, das Gitternetz in den Bereich jenseits der reellen \(x\)-Achse fortzusetzen. Auf diese Weise können wir rekonstruieren, an welcher Stelle \(f(z)\) ein Punkt \(z\) landen muss, damit \(f(z)\) eine analytische Fortsetzung von \(f(x)\) darstellt.
Man kann sich das Vorgehen sehr plastisch so vorstellen: Male ein x-y-Koordinatensystem mit Gitternetz auf ein Holzbrett und kopiere einen Ausschnitt davon auf eine dünne Gummihaut, wobei dieser Ausschnitt den Definitionsbereich von \(f(x)\) auf der \(x\)-Achse enthalten muss.
Nagle nun die Gummihaut entlang der \(x\)-Achse so auf das Brett, dass jeder Punkt \((x, 0)\) der \(x\)-Achse der Gummihaut auf dem Punkt \((f(x), 0)\) der \(x\)-Achse des Holzbretts zu liegen kommt. Dafür müssen wir die Gummihaut in manchen Bereichen dehnen oder stauchen, so wie es die reelle Funktion \(f(x)\) vorgibt. Versuche nun, ausgehen von den bereits festgenagelten Punkten der \(x\)-Achse schrittweise auch die übrige Gummihaut so auf dem Brett festzunageln, dass die Gitternetzlinien sich unter denselben Winkeln schneiden wie vorher.
Schauen wir uns dazu ein konkretes Beispiel an: die geometrische Reihe \[ f(x) = 1 + x + x^2 + x^3 + x^4 + \, ... \] Diese unendliche Reihe konvergiert für \( |x| < 1 \). Wir überziehen nun die komplexe Ebene mit einem Gitternetz. In dem vorliegenden Fall erweist sich eine Art radiales Spinnennetz mit Mittelpunkt \((1, 0)\) als die beste Wahl. Für die Punkte der \(x\)-Achse zwischen -1 und 1 können wir nun in einem zweiten Bild die entsprechenden Punkte \((f(x), 0)\) einzeichnen. Hier sind einige Werte: \(f(-0,6) = 0,625\), \(f(0) = 1\), \(f(0,5) = 2\), \(f(0,8) = 5\) usw.. Generell beginnen die Punkte \(f(x)\) oberhalb von 0,5 und werden dann immer größer, je mehr sich \(x\) dem Wert 1 nähert. Der \(x\)-Achsenbereich zwischen -1 und 1 wird also auf die positive x-Achse oberhalb von 0,5 abgebildet.
Wo landen nun die übrigen Gitternetzpunkte jenseits der \(x\)-Achse?
Die einzige Möglichkeit, die Winkel und Drehsinn
unverändert lässt und die die oben bereits eingezeichneten Punkte mit umfasst,
ist die folgende: Verschiebe das ursprüngliche Gitternetz, so dass sein Mittelpunkt
im Ursprung \((0, 0)\) liegt, führe anschließend eine Spiegelung der Punkte am Einheitskreis durch
(d.h. ein Punkt mit Abstand \(r\) zum Ursprung \((0, 0)\) hat danach den Abstand \(1/r\) zum Ursprung,
liegt aber auf derselben Speiche des Gitters) und führe danach eine Spiegelung an der
\(y\)-Achse durch. Das Ergebnis zeigt das folgende Bild, wobei z.B. ein Punkt links außen
anschließend rechts innen landet.
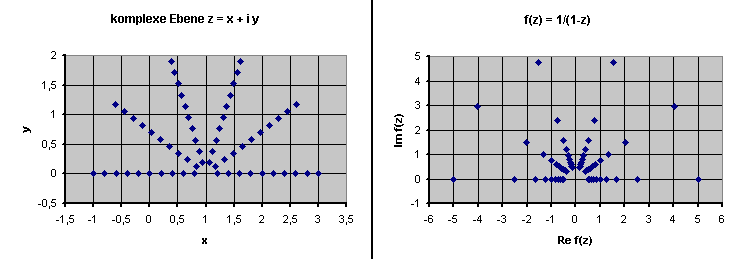
Dieses Bild zeigt also die analytische Fortsetzung \(f(z)\) der geometrischen Reihe. Es zeigt sich, dass \(f(z)\) für alle Punkte außer für \(z = 1\) definiert ist, also auch für \(x\)-Werte, die unterhalb von -1 oder oberhalb von +1 liegen. Für diese \(x\)-Werte war \(f(x)\) zuvor gar nicht definiert gewesen. Die analytische Fortsetzung der geometrischen Reihe hat also auch zu einer reellen Fortsetzung geführt!
Im Fall der geometrischen Reihe kann man die analytische Fortsetzung auch in Formeln leicht nachvollziehen: Es gilt \begin{align} f(x) &= 1 + x + x^2 + x^3 + \, ... = \\ &= 1 + x \cdot (1 + x + x^2 + ... \, ) = \\ &= 1 + x \cdot f(x) \end{align} Diese Gleichung kann man nach \(f(x)\) freistellen mit dem bekannten Ergebnis \[ f(x) = \frac{1}{1 - x} \] Die analytische Fortsetzung dieser Funktion ist \[ f(z) = \frac{1}{1 - z} \] Genau diese Formel haben wir verwendet, um die obigen Bilder zu berechnen.
Nun sind wir gerüstet, uns auf die Suche nach der analytischen Fortsetzung der Riemannschen Zetafunktion zu machen, die zunächst nur für reelle \(s > 1\) über die Reihen-Formel \[ \zeta(s) = 1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \, ... \] definiert ist.
Können wir in dieser Formel statt einem reellen \(s\) einfach ein komplexes \(s\) verwenden? Was bedeuten dann die einzelnen Summanden \[ \frac{1}{n^s} \] mit komplexem \(s\) und einer beliebigen natürlichen Zahl \(n\)?
Bei reellem \(s\) und reellem \(a\) gilt ganz allgemein die Beziehung \[ a^s = e^{s \, \ln (a)} \] mit dem natürlichen Logarithmus \(\ln\) zur Basis \(e\) . Also haben wir füsr reelles \(s\) und einer natürlichen Zahl \(n\) \[ \frac{1}{n^s} = n^{-s} = e^{-s \, \ln (n)} \] Die \(e\)-Funktion ist nun auch für komplexe Zahlen überall definiert (siehe oben), d.h. wir können in der obigen Formel problemlos das reelle \(s\) durch ein komplexes \(s\) ersetzen und erhalten so die analytische Fortsetzung jedes einzelnen Summanden und damit auch der Zetafunktion.
Allerdings konvergiert die Zeta-Reihe nur für diejenigen \(s\), deren Realteil (also \(x\)-Komponente)
größer als 1 ist. Also haben wir bisher nur
die analytische Fortsetzung der Zetafunktion für die \(z\)-Ebene rechts von \(x=1\)
konstruiert. Einen Eindruck davon vermittelt dieses Bild:
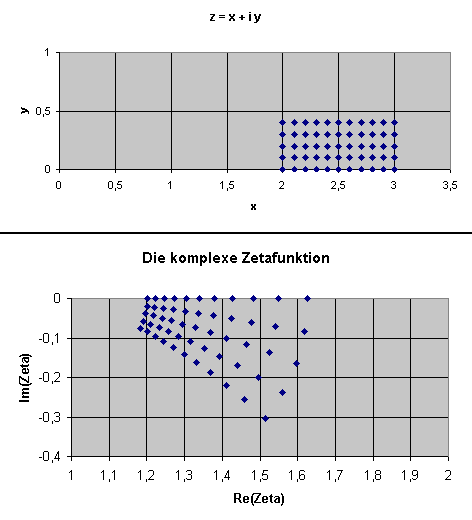
Zeichnet man das Gesamtbild (das wir hier leider nicht angeben können), so sieht man, dass es keinen Grund gibt, nur komplexe \(s\) mit Realteil oberhalb von 1 zuzulassen. Nur bei \(s = 1\) gibt es einen Pol. Für alle anderen \(s\) lässt sich dagegen das Gitternetzbild mit allen oben genannten Anforderungen (Winkeltreue, Drehsinn) problemlos vervollständigen, d.h. die analytische Fortsetzung der Zetafunktion sollte überall (außer bei \(s = 1\)) möglich sein. Doch wie erhält man die entsprechenden Formeln?
Ganz so einfach wie oben bei der geometrischen Reihe ist es leider nicht. Es gibt hier verschiedene Wege, ans Ziel zu gelangen, wobei das Ergebnis immer dasselbe ist, nur in verschiedener Darstellung (die analytische Fortsetzung ist ja eindeutig).
Betrachten wir beispielsweise die folgende Reihe: \[ \eta(s) = 1 - \frac{1}{2^s} + \frac{1}{3^s} - \frac{1}{4^s} + \, ... \] Diese Reihe unterscheidet sich von der Reihe der Zetafunktion dadurch, dass das Vorzeichen der einzelnen Summanden immer zwischen + und - wechselt. Die Reihe konvergiert für alle komplexen \(s\) mit positivem Realteil, also rechts der \(y\)-Achse. Man bezeichnet diese Funktion als Dirichletsche Etafunktion oder auch als alternierende Zetafunktion (siehe auch z.B. Wolfram MathWorld: Dirichlet Eta Function). Diese Funktion ist in ihrem Definitionsbereich überall komplex differenzierbar.
Wir können nun die Reihe der Etafunktion etwas umschreiben, so dass die Reihe der Zetafunktion dabei zweimal entsteht: \begin{align} \eta(s) &= 1 - \frac{1}{2^s} + \frac{1}{3^s} - \frac{1}{4^s} \, ... \, = \\ & \\ &= 1 \;\; + \left(\frac{1}{2^s} - 2 \cdot \frac{1}{2^s} \right) + \\ & + \frac{1}{3^s} + \left(\frac{1}{4^s} - 2 \cdot \frac{1}{4^s} \right) + \, ... \, = \\ & \\ &= \left( 1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \, ... \, \right) + \\ &- 2 \cdot \; \left( \; \frac{1}{2^s} + \frac{1}{4^s} + \frac{1}{6^s} + \, ... \, \right) = \\ & \\ &= \left( 1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \, ... \, \right) + \\ &- \frac{2}{2^s} \cdot \; \left( 1 + \frac{1}{2^s} + \frac{1}{3^s} + \, ... \, \right) = \\ & \\ &= \zeta(s) - 2^{1-s} \, \zeta(s) = \\ & \\ &= (1 - 2^{1-s}) \, \zeta(s) \end{align} Diese Umgruppierung ist natürlich nur für komplexe \(s\) mit Realteil \( > 1\) erlaubt, da ansonsten die \(\zeta(s)\)-Reihe nicht konvergiert.
Die erhaltene Gleichung \( \eta(s) = (1 - 2^{1-s}) \, \zeta(s) \) können wir nach \(\zeta(s)\) freistellen mit dem Ergebnis \[ \zeta(s) = \frac{\eta(s)}{1 - 2^{1-s}} \] Nun gilt diese Gleichung zunächst nur für \(s\) mit Realteil größer als 1, da \(\zeta(s)\) bisher nur für diese \(s\) definiert ist. Wir können aber die obige Gleichung dazu verwenden, um die analytische Fortsetzung von \(\zeta(s)\) auf den Bereich aller komplexen \(s\) mit Realteil größer als 0 auszudehnen, denn \(\eta(s)\) ist in diesem Bereich eine komplex differenzierbare Funktion, ebenso wie der Nenner \(1 - 2^{1-s}\). Einzig der Punkt \(s = 1\) muss dabei herausgenommen werden, denn der Nenner wird hier Null (d.h. die Zetafunktion hat hier einen Pol). Im Grunde spaltet die obige Formel den Pol bei \(s = 1\) ab, denn \(\eta(s)\) hat dort keinen Pol.
Diese Ausweitung der Zetafunktion auf größere Definitionsbereiche ist keineswegs willkürlich, denn die analytische Fortsetzung einer Funktion ist immer eindeutig. Wenn man also den Definitionsbereich einer komplex differenzierbaren Funktion ausweiten kann, dann immer nur auf eine einzige Art und Weise (wobei die Formeln schon unterschiedlich aussehen können – sie definieren aber dieselbe Funktion, nur in unterschiedlicher Darstellung).
Für die Riemannsche Vermutung ist keine weitere Ausweitung des Definitionsbereichs mehr erforderlich, denn diese Vermutung beschäftigt sich mit den Nullstellen der Zetafunktion für \(s\)-Werte mit Realteil zwischen Null und Eins. Dennoch wollen wir uns kurz ansehen, wie man den Definitionsbereich auf alle komplexen \(s\)-Werte (außer \(s = 1\)) ausweiten kann:
Man kann zeigen, dass die Zetafunktion im Streifen parallel zur \(y\)-Achse mit Realteil von \(s\) zwischen Null und Eins eine interessante Punktsymmetrie aufweist. Dazu definiert man die Funktion \[ A(s) := \pi^{-\frac{s}{2}} \, \Gamma \left( \frac{s}{2} \right) \zeta(s) \] Dabei ist \(\Gamma(s)\) die Gammafunktion, die sich als analytische Interpolation der Fakultät natürlicher Zahlen ergibt, wie die Gleichung \[ \Gamma(n) = (n-1)! = \] \[= (n-1) \cdot (n-2) \cdot \, ... \, \cdot 2 \cdot 1 \] zeigt (wobei \(n\) eine natürliche Zahl ist, siehe auch Wolfram MathWorld: Gamma Function). Die Gammafunktion ist überall komplex differenzierbar außer an den Polen bei \(s = 0, -1, -2, -3\) usw.. Außerdem hat die Gammafunktion keine Nullstellen.
Der Grund für die Definition von \(A(s)\) liegt in der folgenden Symmetriebeziehung: \[ A(s) = A(1 - s) \] (siehe Riemann's functional equation in Wikipedia: Riemann zeta function) oder gleichwertig mit \(s = 1/2 + z\) : \[ A(1/2 + z) = A(1/2 - z) \] d.h. \(A\) ist punktsymmetrisch zum Punkt 1/2 .
Nun gilt diese Symmetrie zunächst nur im Streifen aller \(s\) mit Realteil zwischen 0 und 1, denn \(\zeta(s)\) und damit \(A(s)\) ist ja links der \(y\)-Achse (d.h. Realteil von \(s < 0\) ) bisher nicht definiert. Wir können aber \(A(s)\) und damit \(\zeta(s)\) dadurch für alle \(s\) (außer \(s = 1\)) definieren, dass wir diese Gleichung als Definitionsgleichung für alle \(s\) ansehen. Die Werte von \(A(s)\) und damit die von \(\zeta(s)\) links der y-Achse können wir per Punktspiegelung aus den bereits bekannten Werten rechts der \(s=1\)-Achse ermitteln. Außerdem kann man beweisen, dass die so definierte Zetafunktion überall komplex differenzierbar ist (außer im Pol bei \(s = 1\)).
Wie sieht nun die Riemannsche Zetafunktion in der komplexen \(s\)-Ebene aus? Die wichtigsten Eigenschaften sind hier kurz zusammengefasst:
Die folgende Grafik aus Wikipedia: Riemannsche Zeta-Funktion
gibt einen Überblick über
die Zetafunktion:
Was sieht man auf diesem Bild?
Auf der negativen \(x\)-Achse erkennt man die trivialen Nullstellen bei \(s = -2, -4, -6, -8, \, ... \) . Ebenso sind die nicht-trivialen Nullstellen im kritischen Streifen nach oben und unten gut zu sehen. Schaut man genauer hin, dann sieht man, dass letztere auf einer Geraden parallel zur \(y\)-Achse mit Realteil 1/2 liegen. Ob dies für alle nicht-trivialen Nullstellen gilt, weiß man nicht, doch es spricht sehr vieles dafür, wie wir weiter unten noch sehen werden. Daher vermutet man:
Der Beweis dieser Vermutung ist eine Millionen US-Dollar wert!
Anders ausgedrückt sagt die Riemannsche Vermutung:
Wenn man in der Mitte des
kritischen Streifens nach oben geht (also genau da, wo die nichttrivialen Nullstellen
liegen sollen, d.h. \(s = 1/2 + i t\) mit reellem \(t\))
und beobachtet, wie sich die Pfeilspitze des Pfeils \(\zeta(s)\)
dabei bewegt, dann wird diese Pfeilspitze dabei eine Art kreisende Bewegung ausführen und immer
wieder durch den Nullpunkt gehen, wenn eine Nullstelle erreicht ist.
Läge eine Nullstelle dagegen nicht genau in der Mitte des kritischen Streifens, so würde die Pfeilspitze
die Null verfehlen.
Hier die entsprechende Grafik:
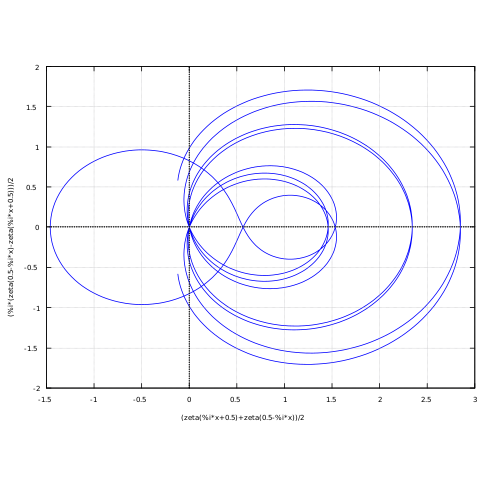
Quelle: Wikimedia File:ParametricZeta.svg,
Autor: Sandroamt, CC BY-SA 4.0.
Die Riemannsche Vermutung sagt also, dass alle Nullstellen des kritischen Streifens den Realteil 1/2 besitzen. Der Beweis diese Vermutung wird als eines der wichtigsten offenen Probleme der Mathematik angesehen. Warum ist das so?
Die Riemannschen Vermutung enthält sehr viele wichtige Informationen über die Strukur der natürlichen Zahlen. Erinnern wir uns: Die Positionen der Primzahlen legen die Riemannsche Zetafunktion eindeutig fest. Gleichzeitig sind die Primzahlen die multiplikativen Atome der natürlichen Zahlen, denn jede natürliche Zahl lässt sich auf genau eine Weise als Produkt von Primzahlen schreiben. Die Information über diese Atome ist in der Zetafunktion gleichsam kodiert und wird über die Methode der analytischen Fortsetzung auf der komplexen Zahlenebene verteilt. In dieser zweidimensionalen Ebene hat man viel mehr Bewegungsspielraum als nur auf der reellen Zahlenachse, so dass dadurch die Informationen den mächtigen Werkzeugen der komplexen Analysis zugänglich werden. Diese Werkzeuge reagieren empfindlich auf Pole und Nullstellen, d.h. in den Positionen der Nullstellen der Zetafunktion stecken viele zentrale Informationen über Primzahlen und damit auch über natürliche Zahlen. Man könnte sagen, in den Polen und Nullstellen kondensiert sich diese Information. Dies zeigt auch die folgende physikalisch motivierte Veranschaulichung des Zusammenhangs zwischen Primzahlverteilung und Nullstellen der Zetafunktion:
Präzisiert wird diese Aussage durch die sogenannte explizite Formel (auch Riemannsche Formel genannt, veröffentlicht von Riemann im Jahr 1859 und durch von Mangoldt im Jahr 1895 bewiesen), die den Zusammenhang zwischen den nichttrivialen Nullstellen der Zetafunktion und der Primzahlverteilung \(\pi(x)\) herstellt. Gleichwertig dazu ist die Formel mit der Riemann-Funktion \(R(x)\), die wir oben bereits kennengelernt haben, wobei die Summe über alle nicht-trivialen Nullstellen \(\rho\) der Riemannschen Zetafunktion \(\zeta(s)\) geht (dabei ist \( x > 1 \)): \[ \pi_0(x) = R(x) - \sum_\rho R(x^\rho) + \] \[ - \frac{1}{\ln (x)} + \frac{1}{\pi} \arctan \frac{\pi}{\ln (x)} \] Wir haben dabei die Terme ohne den Summenterm \( \sum_\rho R(x^\rho) \) als die bestmögliche glatte Näherung der Primzahlverteilung \( \pi(x) \) interpretiert und den Summenterm, der über die nichttrivialen Nullstellen der Zetafunktion geht, als Fehlerterm oder statistisches Rauschen angesehen.
Je mehr nichttriviale Nullstellen \(\rho\) der Zetafunktion man hinzunimmt, umso genauer kann
man also die wahre Primzahlverteilung \(\pi(x)\) reproduzieren.
In niedrigster Näherung (also ohne jede Nullstelle) wird \(\pi(x)\) durch
die Riemannfunktion \(R(x)\) und die anderen glatten Terme approximiert. Nimmt man die erste Nullstelle hinzu,
so ergeben sich kleine Oberwellen, die versuchen, die Stufen der Primzahlverteilung \(\pi(x)\)
grob zu imitieren, was bei den ersten Stufen auch ganz gut gelingt.
Nimmt man weitere Nullstellen und damit feinere Oberwellen hinzu,
so werden die Stufen immer genauer beschrieben.
Hier das Ergebnis, wenn man 50 Nullstellenpaare (sie liegen ja spiegelbildlich zur \(x\)-Achse)
berücksichtigt:
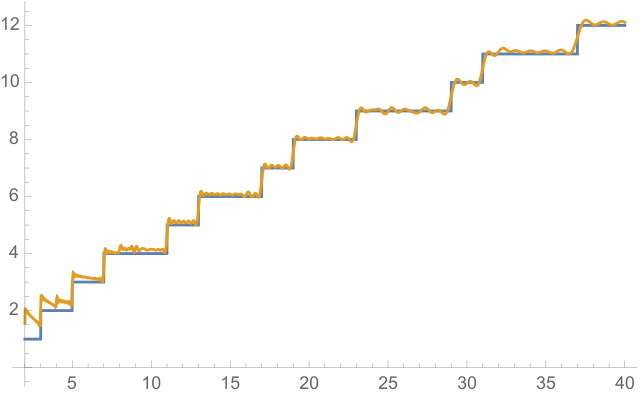
Quelle:
Wikimedia Commons File:PrimePiRiemannRcorr.svg,
Auto: Googolplexian1221,
CC BY-SA 4.0.
Letztlich geht es bei der Riemannschen Vermutung also um die Verteilung der Primzahlen im Meer der natürlichen Zahlen. Dieses Meer ist über die Addition definiert, denn von Zahl zu Zahl wird immer wieder 1 hinzugezählt – eben der ganz normale Prozess des Zählens. Die Primzahlen sind dagegen über die Multiplikation definiert, denn sie sind über die Primfaktorzerlegung die multiplikativen Bausteine der natürlichen Zahlen. Die Verteilung der Primzahlen und damit die Riemannsche Vermutung sagt also etwas über die Wechselbeziehung von Addition und Multiplikation natürlicher Zahlen aus. Beide für sich sind unproblematisch, aber beide zusammen sind unglaublich komplex und bis heute nicht vollständig durchdrungen, wie der fehlende Beweis für die Riemannsche Vermutung eindrucksvoll zeigt.
Diese Rekonstruktion der Primzahlverteilung über die nichttrivialen Nullstellen der Zetafunktion bewirkt – wie wir ja bereits wissen – dass beispielsweise die Fehlerabschätzung im Primzahlsatz von den Positionen der nichttrivialen Nullstellen der Zetafunktion abhängt. Aber auch viele andere Beweise der Zahlentheorie verwenden die Riemannsche Vermutung als Annahme – kein Wunder, wenn diese gleichsam an der Schnittstelle von Addition und Multiplikation natürlicher Zahlen sitzt.
Die Riemannsche Vermutung ist zudem keine isolierte Fragestellung. Sie ist eine Art Prototyp für eine allgemeine Klasse von Funktionen (den sogenannten L-Funktionen), die etwas mit der algebraischen Darstellung arithmetischer Objekte zu tun haben. Auf Details wollen wir hier nicht eingehen.
Allein schon die Tatsache, dass die Riemannsche Vermutung bis heute allen Beweisversuchen erfolgreich widerstanden hat, macht sie so interessant. Man hat heute den Eindruck, dass vollkommen neue Beweisideen und Beweisverfahren zu ihrer Lösung notwendig sind. Vermutlich müssen erst sehr allgemeine und umfangreiche Probleme geknackt werden, damit gleichsam nebenbei auch die Riemannsche Vermutung bewiesen werden kann (so war es beispielsweise bei der Fermatschen Vermutung).
Man geht heute davon aus, dass die Riemannsche Vermutung zutrifft. Dafür gibt es mehrere Gründe:
Die Riemannsche Vermutung ist nun gleichwertig zu der Aussage, dass sich \(M(N)\) statistisch wie eine stochastische Irrfahrt verhält, bei der ein Betrunkener zufällig mit gleicher Wahrscheinlichkeit mal eine Schritt nach oben, mal einen Schritt nach unten macht. Statistische Untersuchungen der Möbiusfunktion legen diese Vermutung nahe. Das bedeutet, dass die genaue Lage der Primzahlstufen in einem bestimmtem Sinn zufällig (oder genauer: pseudozufällig) erscheint.
Besteht Hoffnung, die Riemannsche Vermutung beweisen zu können, oder erweist sie sich womöglich als unabhängig von den Axiomen der Mengenlehre, analog zur Kontinuumshypothese?
Einige Mathematiker glauben, dass ein Beweis in nicht allzu ferner Zukunft möglich sein könnte. So wurden Analogien zwischen den nichttrivialen Nullstellen und quantenmechanischen chaotischen Systemen entdeckt: Der Mathematiker Hugh Montgomery und der Physiker Freeman Dyson machten im Jahr 1972 die Beobachtung, dass die Abstände zwischen den Nullstellen der Zeta-Funktion genauso aussehen wie die Abstände zwischen den Energieniveaus in quantenchaotischen Systemen. Die Nullstellen scheinen sich gleichsam abzustoßen, haben also statistisch die Tendenz, nicht zu nahe beieinander zu liegen. Mathematisch präziser ausgedrückt: Die nichttrivialen Nullstellen der Zetafunktion scheinen dieselben statistischen Eigenschaften aufzuweisen wir die Eigenwerte von hermiteschen Zufallsmatrizen. Ob sich diese Analogie für einen Beweis nutzen lässt, ist allerdings noch unklar. Fände sich jedoch beispielsweise eine quantenchaotische Anordnung, deren Energieniveaus exakt mit den Nullstellen der Zeta-Funktion übereinstimmen, wäre die Riemannsche Vermutung bewiesen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 05 April 2023