
Quelle: Wikipedia Commons File:Poincare.jpg, dort Public Domain (Copyright abgelaufen).
Auch in diesem Kapitel wollen wir uns ein weiteres berühmtes mathematisches Problem ansehen, das ebenfalls zu den sieben Millenium Prize Problems gehört: die Poincaré-Vermutung (siehe CMI: Poincaré Conjecture). Wieder gab es eine Million US-Dollar für den Beweis (oder die Widerlegung) dieser Vermutung zu verdienen. Ende 2002 ist es dann dem russischen Mathematiker Grigori Perelman gelungen, einen Beweis zu finden. Das Geld für seine Entdeckung lehnte der eigensinnige und zugleich geniale Mathematiker ebenso ab wie die Fields-Medaille (gleichsam der Mathematik-Nobelpreis), die er zur Anerkennung seines Beweises erhalten sollte.
Die Poincaré-Vermutung bewegt sich auf dem Gebiet der Topologie von Mannigfaltigkeiten. Vereinfacht gesagt, behauptet sie Folgendes (Details folgen später):
Diese Vermutung wurde im Jahr 1904 von dem berühmten französischen Mathematiker Henri Poincaré aufgestellt, als er sich mit der großräumigen Gestalt von Flächen und Räumen (Mannigfaltigkeiten) beschäftigte.

Um diese Vermutung zu verstehen, müssen wir uns genauer anschauen, was dreidimensionale in sich gekrümmte Räume sein sollen, und was genau die 3-Sphäre ist.
Was also verstehen wir unter einem dreidimensionalen, ggf. in sich gekrümmten Raum ohne Rand? Oder mathematisch ausgedrückt: Was ist eine einfach zusammenhängende kompakte dreidimensionale Mannigfaltigkeit?
Hier hilft die Analogie zu entsprechenden zweidimensionalen Räumen weiter, da wir uns diese zumeist (aber nicht immer!) als (ggf. gekrümmte) Flächen im dreidimensionalen gewöhnlichen Raum vorstellen können.
Ein schönes zweidimensionales Beispiel ist die Kugeloberfläche, die auch 2-Sphäre genannt wird. Betrachten wir nur einen sehr kleinen Teil der Kugeloberfläche, so erscheint dieser Teil nahezu wie ein Ausschnitt der zweidimensionalen flachen Ebene, da bei einem so kleinen Teil die Krümmung der Fläche kaum auffällt. Nicht umsonst haben wir Menschen in der Geschichte oft angenommen, dass die Erde eine flache Scheibe sei, denn für uns ist die Krümmung der Erdoberfläche kaum wahrnehmbar. Erst wenn wir größere Teile der Erdoberfläche betrachten, wird die Krümmung sichtbar.
Zweidimensionale Flächen sind also im Kleinen (d.h. lokal) vom zweidimensionalen euklidischen Raum (also von der flachen Ebene) kaum zu unterscheiden. Oder umgekehrt: Genau dies verlangen wir von zweidimensionalen Räumen. Analog gehen wir bei dreidimensionalen Räumen vor: Auch diese sollen lokal so wie der gewohnte dreidimensionale euklidische Raum aussehen. Für einen Beobachter, der nur einen sehr kleinen Teil eines dreidimensionalen Raumes überblicken kann, sieht dieser Teil also wie ein Teil des gewohnten dreidimensionalen euklidischen Raumes aus. Dies soll für jeden kleinen Ausschnitt des Raumes gelten – man könnte dies auch als Homogenitätsforderung bezeichnen.
Wenn man einen Punkt auf einer zweidimensionalen Fläche angeben will, so benötigt man ein Koordinatensystem mit zwei Koordninaten auf der Fläche. Bei der Erdoberfläche sind dies beispielsweise die Längen- und Breitengrade. Manchmal reicht ein einziges Koordinatensystem nicht aus, um eine komplizierte Fläche vollständig zu erfassen. In diesem Fall verwendet man mehrere Koordinatensysteme, die sich auch überlappen können. In den Überlappungsbereichen braucht man eine Vorschrift, wie man von einem Koordinatensystem zum anderen wechseln muss. Insgesamt muss jeder Teil der Fläche von mindestens einem Koordinatensystem erfasst werden. Man bezeichnet eine solche Sammlung von Koordinatensystemen für eine Fläche auch als Atlas, wobei man wieder an die Erdoberfläche denken kann, deren Teile in einem Schulatlas auf vielen verschiedenen Karten (und damit mit vielen verschiedenen Koordinatensystemen) dargestellt sind. Jede Karte des Atlas entspricht dabei einem Koordinatensystem für einen Teil der Fläche.
Ein solcher Atlas soll auch für unsere dreidimensionalen Räume vorhanden sein. Statt zwei Koordinaten werden allerdings nun drei Koordinaten benötigt.
Nehmen wir nun an, ein Auto bewegt sich auf der Erdoberfläche auf einer glatten Bahn, d.h. es wendet nirgends und hält nirgends an. Seine Bahn soll also keine Ecken oder Spitzen aufweisen. Dann fordern wir, dass es einen Atlas gibt, so dass die Bahn des Autos auf jeder Karte, auf der die Bahn auftaucht, ebenfalls glatt ist. Die Karten sollen also keine scheinbaren Ecken in die Bahn des Autos einbringen. Wir bezeichnen dies als Glattheitsforderung. Diese Glattheitsforderung soll analog auch für dreidimensionale Räume und die zugehörigen Korrdinatensysteme gelten.
Weiterhin soll der Raum kompakt, randlos und endlich sein. Auf die mathematisch präzise Bedeutung dieser Begriffe wollen wir hier nicht näher eingehen. Anschaulich bedeuten sie, dass der Raum nicht irgendwo eine Begrenzung haben darf (eine Fläche soll also keine Kanten haben), und dass der Rauminhalt (oder der Flächeninhalt) endlich sein soll.
Und schließlich soll der Raum orientierbar sein. Das bedeutet, dass sich der Drehsinn nicht ändern kann, wenn wir auf einem Rundweg durch den Raum wandern und schließlich zu der ursprünglichen Stelle zurückkehren. Zweidimensionale Flächen, die wir uns als Oberfläche von dreidimensionalen Objekten vorstellen können, sind immer orientierbar. Man kann aber auch zweidimensionale kompakte, randlose endliche Flächen angeben, die nicht orientierbar sind. Ein Beispiel dafür ist die sogenannte Kleinsche Flasche. Diese Fläche lässt sich nicht ohne Überschneidungen im dreidimensionalen Raum eingebettet darstellen, sondern man benötigt dafür vier Dimensionen. Es gibt bei ihr kein Inneres und kein Äußeres.
Man kann nun Flächen, Räume oder allgemein Mannigfaltigkeiten unter verschiedenen Gesichtspunkten untersuchen. So kann man sich für Begriffe wie Krümmung, Volumen, Abstand oder Winkel interessieren – diese Begriffe legen die Geometrie (oder Metrik) eines Raums fest. Die Geometrie ändert sich zumeist, wenn wir anfangen, den Raum oder die Fläche kontinuierlich zu verformen (ohne dabei irgendwo Teile auseinanderzureißen). Allgemein ist die Geometrie eine lokale Eigenschaft, die an verschiedenen Stellen des Raums unterschiedlich sein kann.
Es gibt aber auch globale Eigenschaften, die eine Fläche oder Raum als Ganzes aufweist und die nicht von der Stelle abhängen, an der wir den Raum betrachten. Diese Eigenschaften ändern sich auch nicht, wenn wir den Raum kontinuierlich verformen. Sie machen die Topologie des Raumes aus. Ein Beispiel für eine solche Eigenschaft ist der Zusammenhang (engl. connectedness) des Raums: Lässt sich jede geschlossene Kurve (Seilschlinge) in dem Raum kontinuierlich zu einem Punkt zusammenziehen?
Betrachten wir als Beispiel die zweidimensionalen orientierbaren endlichen randlosen Flächen, also die Flächen, die wir uns als Oberflächen von endlichen dreidimensionalen Objekten vorstellen können. Wir wollen uns dabei nicht für die lokale Geometrie interessieren, sondern für die verschiedenen denkbaren Topologien dieser Flächen. Welche topologisch unterschiedlichen Flächen gibt es hier? Wie lassen sich diese Flächen topologisch klassifizieren?
Seit dem Zeitraum um das Jahr 1900 herum weiß man, dass die Zahl der Löcher (auch Genus genannt) in dem dreidimensionalen Objekt die Topologie der Oberfläche eindeutig kennzeichnet. Der einfachste Fall (Genus Null) ist die Kugeloberfläche (2-Sphäre). Hier gibt es kein Loch. Als nächstes kommt der Torus (Genus 1, sieht aus wie ein Kringel oder Donut): er hat ein Loch. Und schließlich kann man zwei oder mehrere Tori miteinander verschmelzen, um mehrere Löcher zu erhalten:

Jede beliebige endliche orientierbare randlose Fläche lässt sich kontinuierlich zu einem der obigen Objekte mit keinem, einem, zwei oder mehr Löchern verformen.
Am Beispiel des Torus (also ein Loch) kann man sich auch den Begriff einfach zusammenhängend schön veranschaulichen. So ist die Torusoberfläche nicht einfach zusammenhängend, denn es gibt zwei Sorten von geschlossenen Kurven, die sich nicht auf der Torusoberfläche kontinuierlich auf einen Punkt zusammenziehen lassen. Hier ist eine davon (in rot):
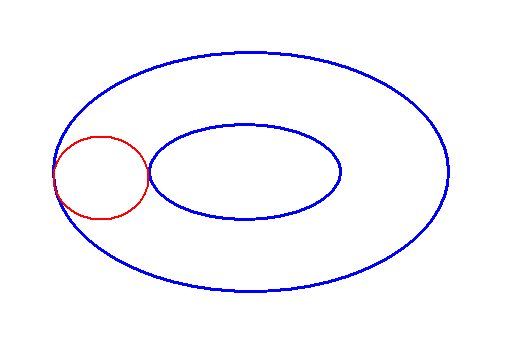
Die Kugeloberfläche dagegen ist einfach zusammenhängend.
Wie sieht es nun mit der Topologie der dreidimensionalen Räume aus? Lassen diese sich ähnlich wie die zweidimensionalen Räume (Flächen) topologisch klassifizieren?
Bevor wir uns dieser Frage im Detail zuwenden, wollen wir zunächst versuchen, eine gewisse anschauliche Vorstellung von dreidimensionalen in sich gekrümmten Räumen zu gewinnen, damit uns die Bedeutung dieser Frage klarer wird. Wir wollen dies am Beispiel der 3-Sphäre tun, die das dreidimensionale Analogon zur Kugeloberfläche (2-Sphäre) ist. Außerdem geht es ja in der Poincaré-Vermutung um die 3-Sphäre.
Mathematisch kann man die 3-Sphäre als Punktemenge im vierdimensionalen
euklidischen Raum definieren. Punkte im vierdimensionalen Raum können wir durch vier
karthesische Koordinaten
Die Kugeloberfläche können wir uns als Objekt eingebettet im dreidimensionalen euklidischen Raum veranschaulichen. Leider können wir uns aber einen vierdimensionalen Raum nicht unmittelbar vorstellen, so dass wir uns die 3-Sphäre nicht durch Einbettung dieses dreidimensionalen Raumes in den vierdimensionalen Raum veranschaulichen können. Wir müssen also zu anderen Methoden der Veranschaulichung greifen, die sich vom zweidimensionalen Fall auf den dreidimensionalen Fall übertragen lassen, ohne dass ein vierdimensionaler Einbettungsraum dazu notwendig ist.
Eine Methode besteht darin, eine der Koordinaten herauszugreifen und Schnittbilder
für verschiedene feste Werte dieser einen Koordinate zu zeichnen.
Bei der Kugeloberfläche könnten wir beispielsweise die
Lässt man die Schnittebene langsam vom Südpol der Kugel zum Nordpol der Kugel wandern,
also von
Analog kann man auch bei der 3-Sphäre vorgehen. Hier würden wir die
Koordinate
Die obige Darstellungsweise mit Schnittbildern in einem Einbettungsraum hat allerdings einen Nachteil: Eine Koordinate muss ausgezeichnet werden, um das Schnittbild festzulegen. Leider hat man so keinerlei Vorstellung davon, wie man sich in der 3-Sphäre insgesamt in allen drei Richtungen bewegen kann. Hier hilft eine andere Methode weiter. Schauen wir uns zunächst an, wie diese Methode bei der Kugeloberfläche funktioniert:
Stellen wir uns vor, wir wollen die Kugeloberfläche aus vielen kleinen flachen Papierstücken zusammensetzen. Dazu müssen wir wissen, wie diese Papierstücke aussehen, und wie wir sie an den Kanten zusammenkleben müssen. Wenn wir die flachen Papierstücke klein genug machen, wird das daraus zusammengeklebte Objekt nur noch leicht kantig sein und einer Kugeloberfläche umso näher kommen, je kleiner die Papierstücke sind. Das liegt daran, dass die Kugeloberfläche lokal (also im Kleinen betrachtet) ja wie der zweidimensionale euklidische Raum aussehen muss. Das folgende Bild zeigt, wie diese Konstruktion aussehen könnte:

Aber auch andere Konstruktionen sind denkbar, z.B. analog zum Aufbau eines Fußballs,
den man ja auch aus einzelnen Lederstücken zusammensetzt.
Die obige Konstruktion orientiert sich an den Längen- und Breitengraden
der Erdoberfläche, oder mathematisch ausgedrückt: an den üblichen Kugelkoordinaten.
Diese Kugelkoordinaten
weichen von den Längen- und Breitengraden in den folgenden Punkten ab:
Erstens wird in Bogenmaß gerechnet, d.h. 360 Grad entspricht im Bogenmaß dem
Winkel
Bei der Oberfläche der Einheitskugel (Radius 1) ist der
Zusammenhang zwischen den beiden Kugelkoordinaten
Betrachten wir die einzelnen Stücke, so sehen wir, dass sie wie kleine gleichschenklige Trapeze aussehen, die auf der Nordhalbkugel in Richtung Nordpol spitzer werden, und auf der Südhalbkugel umgekehrt. Direkt an den Polen haben sie sogar eine echte Spitze. Am Äquator dagegen sind sie fast rechteckig.
Einen guten Überblick über die Ausschnitte der Kugeloberfläche und wie sie zusammengehören
erhält man, wenn man die Stücke wie folgt auf einem Blatt Papier anordnet:
Ein Stück, dessen Mittelpunkt bei den Kugelkoordinaten
Nehmen wir nun an, wir wollten einem zweidimensionalen Wesen erklären, wie eine Kugeloberfläche aussieht. Dieses Wesen kann sich allerdings nur zweidimensionale Objekte vorstellen, d.h. es wird ihm unmöglich sein, sich die Kugeloberfläche im dreidimensionalen Raum vorzustellen.
Wir könnten diesem Wesen nun die in kleine flache Papierstücke zerlegte Kugeloberfläche (z.B. in Form der oben beschriebenen Rosette) zeigen und ihm sagen, wie diese Stücke zusammengehören, d.h. wo man von der Kante eines Papierstücks auf das nächste Papierstück wechseln muss. Auf diese Weise kann das Wesen nachvollziehen, wie man sich auf der Kugeloberfläche bewegen kann, ohne dass es sich die Kugeloberfläche als Ganzes vorstellen muss. Wir können ihm z.B. zeigen, wie man sich auf der Oberfläche immer geradeaus bewegen kann und dabei nach einer Umdrehung wieder am Ausgangspunkt landet. Auf diese Weise kann das Wesen zumindest eine gewisse Vorstellung von der Kugeloberfläche gewinnen. Es sieht z.B. auch, dass die Fläche endlich ist, ohne irgendwo Grenzen zu haben, denn jede Kante ist mit der Kante eines anderen Papierstücks zu verkleben, so dass es keine Ränder der Fläche gibt.
Diese Methode können wir nun auf die 3-Sphäre übertragen. Hier befinden wir uns genau in der Lage dieses Wesens: Wir können uns den vierdimensionalen Raum mit der darin eingebetteten dreidimensionalen 3-Sphäre nicht vorstellen. Aber wir können die 3-Sphäre in kleine dreidimensionale Stücke zerlegen und angeben, wie wir an den Seitenflächen von einem Stück zum nächsten wechseln müssen, d.h. wie die Stücke zusammengehören. Wirklich zusammenkleben können wir sie dabei im dreidimensionalen Raum aber nicht, so wie sich auch die Stücke der Kugeloberfläche nicht auf einem zweidimensionalen Papier liegend zusammenkleben lassen. Es würden Lücken übrig bleiben, die sich nur ein einem höherdimensionalen Raum schließen lassen (d.h. beim Zusammenkleben fängt die Kugeloberfläche an, sich zu krümmen).
Wie sehen nun die Stücke der 3-Sphäre aus?
Auch hier gibt es verschiedene Möglichkeiten. Wir wollen hier eine Verallgemeinerung
der Kugelkoordinaten verwenden, um die Zerlegung durchzuführen.
In Kugelkoordinaten lauten die Punkte der 3-Sphäre im vierdimensionalen Raum wie folgt:
Wie können wir diese Koordinaten verstehen?
Zunächst einmal wird
Wie sehen nun
Wie sieht nun ein kleiner Ausschnitt der 3-Sphäre aus?
Betrachten wir zunächst die Grundfläche dieses Ausschnitts, bei der wir
Betrachten wir nun, wie der kleine Ausschnitt senkrecht zur Grundfläche (also in die dritte Dimension,
d.h. in
Für
Wie können wir uns nun die gesamte Zerlegung der 3-Sphäre vorstellen?
Wir können die einzelnen dreidimensionalen Ausschnitte im dreidimensionalen
Raum in Analogie zur Rosettenanordnung der Kugeloberfläche
positionieren, um einen Gesamtüberblich zu bekommen:
Einen Ausschnitt, der z.B. seinen Mittelpunkt bei bestimmten
Werten
Die ganze Konstuktion sieht aus wie ein Seeigel.
Die einzelnen Stacheln stecken mit ihren Spitzen dicht an dicht im Mittelpunkt
zusammen.
Im Querschnitt (senkrecht zur radialen

Man könnte den Seeigel auch etwas abwandeln: Man bricht alle Stacheln in der Mitte (also an der dicksten Stelle) durch und klebt die äußeren Stücke tatsächlich an ihren Spitzen zu einem zweiten Seeigel zusammen, der dann genauso aussieht wie der übriggebliebene Rest des ersten Seeigels. Beide Seeigel haben dann stumpfe Stacheln, und man müsste sie sich an den Bruchstellen jedes einzelnen Stachels zusammengeklebt vorstellen.
Für topologische Überlegungen, bei denen die lokale Geometrie der 3-Sphäre keine Rolle spielt
(d.h. bei denen es auf kontinuierliche Verformungen nicht ankommt),
kann man das Bild der 2 Seeigel noch etwas vereinfachen:
Man verformt die stumpfen Stachelhälften der beiden Seeigel, so dass die Zwischenräume zwischen
ihnen verschwinden. Die Stacheln werden also so verbreitert, dass jeder der beiden Seeigel zu einer
Kugel mit Radius
Auch hierzu gibt es das entsprechende zweidimensionale Analogon bei der Kugeloberfläche. Man kann eine Kugel topologisch durch zwei ausgefüllte Kreisflächen beschreiben, bei denen man die Randpunkte miteinander identifiziert. Dies kann man sich sogar ganz real veranschaulichen: Stellen wir uns vor, die beiden Kreisflächen seien aus Gummi wie die Hülle eines Luftballons. Dann legen wir die beiden Gummi-Kreisflächen einfach übereinander und verkleben die Ränder fest miteinander. Nun können wir Luft zwischen die beiden Gummiflächen pusten, so dass sich das Gebilde nach und nach zu einer richtigen Kugel aufbläht. Dieses Aufblähen ändert ja nichts an den topologischen Eigenschaften des Gebildes. Die linke Kreisfläche wird dabei zur linken Halbkugeloberfläche, die rechte zur rechten Halbkugeloberfläche, siehe das folgende Bild (siehe dazu auch ähnliche Darstellungen im Internet unter Visualizing the N-Sphere).
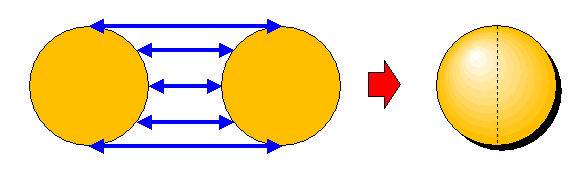
Zurück zur 3-Sphäre: Anhand der obigen Veranschaulichungen kann man sich überlegen, dass sich jede geschlossene Kurve (Seilschlinge) kontinuierlich innerhalb der 3-Sphäre zusammenziehen lässt. Die 3-Sphäre ist einfach zusammenhängend.
Nun sind natürlich außer der 3-Sphäre noch weitere dreidimensionale endliche, in sich gekrümmte, orientierbare randlose Räume denkbar. Auch sie können wir uns durch eine Ansammlung von dreidimensionalen Bausteinen zusammen mit einer Klebe-Vorschrift für diese Bausteine veranschaulichen, analog zum Seeigel-Modell für die 3-Sphäre. Die Frage von Poincaré lautet nun:
Warum sollte die Vermutung zutreffen? Nun, im zweidimensionalen Fall trifft sie zu: Jede zweidimensionale endliche Oberfläche, die einfach zusammenhängen ist (deren durch die Fläche umhüllter Körper also keine Löcher wie ein Donut oder eine Brezel hat), ist eine mehr oder weniger deformierte Version der Kugeloberfläche.
Wir wissen dies, weil – wie oben bereits erwähnt – die Zahl der Löcher (d.h. der Genus) in dem dreidimensionalen Objekt die Topologie der zweidimensionalen Oberfläche dieses Objektes eindeutig kennzeichnet. Alle Objekte mit Genus Null (also ohne Loch, z.B. die Kugeloberfläche) sind damit topologisch gleich. Dies sind aber gerade die einfach zusammenhängenden Oberflächen. Alle einfach zusammenhängenden endlichen orientierbaren Oberflächen sind damit topologisch gleich der Kugeloberfläche, d.h. sie sind kontinuierlich deformierte Versionen der Kugeloberfläche.
Ob das aber auch für den dreidimensionalen Fall gelten muss, ist keineswegs sofort klar. Dreidimensionale Räume können deutlich komplizierter sein als zweidimensionale Flächen. Die zusätzliche Raumdimension eröffnet neue Möglichkeiten, wie der Raum in sich selbst gekrümmt sein kann. Um die Poincaré-Vermutung zu beweisen oder zu widerlegen wäre es sicher hilfreich, eine Übersicht über die möglichen topologischen Varianten dreidimensionaler Räume zur Verfügung zu haben. Genau genommen ist dies auch das eigentliche Problem:
Welche möglichen globalen Grundformen können diese Räume aufweisen (unabhängig von kontinuierlichen Deformationen dieser Grundformen)? Welche grundlegenden Zusammen-Klebe-Möglichkleiten für die Bausteine gibt es?
Die Situation erweist sich als recht kompliziert. Es gibt aber eine berühmte sehr tiefgehende Vermutung von William Thurston aus dem Jahr 1983, die dazu eine Aussage macht. Hier ist eine (mathematisch unpräzise) Kurzform dieser Vermutung (siehe z.B. Wolfram MathWorld: Thurston's geometrization conjecture):
Falls diese Vermutung richtig ist, so folgt (gleichsam als Nebenprodukt) die Poincaré-Vermutung. Das eigentliche und umfassendere Problem ist also der Beweis von Thurstons Vermutung.
Ende 2002 ist es Grigori Perelman tatsächlich gelungen, das Rätsel zu lösen und Thurstons Vermutung (und damit zugleich die Poincaré-Vermutung) zu beweisen. Sein Ansatz ist ebenso tiefgehend wie sorgfältig durchdacht. Perelman verwendet dabei mächtige mathematische Werkzeuge wie den sogenannten Ricci-Fluss (Ricci-Flow). Der Ricci-Fluss verhält sich ungefähr so wie der Wärmefluss bei einem Körper, der an verschiedenen Stellen unterschiedlich warm ist. Nur tritt an die Stelle der Wärme des Körpers die (positive) Krümmung des Raums (Anm.: eine Kugeloberfläche besitzt überall positive Krümmung, eine Satteloberfläche dagegen negative Krümmung). Der Ricci-Fluss bewirkt, dass sich die positive Krümmung in einem dreidimensionalen Raum ausbreitet, d.h. der Raum verformt sich entsprechend. Anders ausgedrückt: Der Raum schrumpft in Richtungen mit positiver Krümmung. Diese Verformung tendiert dazu, den Raum so gleichmäßig wie möglich zu machen, so wie auch der Wärmefluss versucht, die Temperatur anzugleichen. So würde der Ricci-Fluss die zweidimensionale Oberfläche eines Hühnereis langsam zu einer Kugeloberfläche verformen. Die auf diese Weise gleichmäßig gemachten Räume lassen sich nun besser untersuchen und klassifizieren.
Allerdings können bei dieser Verformung Spitzen oder immer dünner werdende Flaschenhälse (Singularitäten) auftreten, die zu Komplikationen führen. Nicht immer gelingt es dem Ricci-Fluss, den Raum gleichförmiger zu machen. Betrachten wir beispielsweise die Oberfläche einer Hantel, bestehend aus zwei dicken Kugeln, die mit einer dünnen Stange miteinander verbunden sind. In diesem Fall kann es geschehen, dass die beiden Kugeln immer dicker werden, während die Verbindungsstange immer dünner wird.
Man könnte versuchen, die Verbindungsstange erst herauszunehmen, den Ricci-Fluss wirken zu lassen und am Schluss die Stange wieder einzusetzen (diese Idee stammt u.a. von dem Mathematiker Richard Hamilton). Aber im dreidimensionalen Fall ist die Sache komplizierter. Man weiß nicht so genau, was für Sorten von Verbindungsstangen es gibt, bei denen der Ricci-Fluss zu Problemen führt. Also weiß man nicht genau, wann man was herausnehmen muss, bevor man den Ricci-Fluss wirken lässt.
Um diese Komplikationen beherrschbar zu machen, verwendet Perelman einen Begriff in Analogie zur statistischen Physik: die Entropie. In der Physik ist die Entropie ein Maß für die mikroskopische Unordnung und damit für die makroskopische Gleichförmigkeit eines komplexen Systems – ein sehr schönes Beispiel dafür, wie sich Physik und Mathematik gegenseitig bereichern können. Perelman zeigt, dass die Entropie eines Raums bei der Verformung durch den Ricci-Fluss ständig anwächst, so wie auch die Entropie eines isolierten makroskopischen physikalischen Objektes in der Natur ständig wächst, bis ein Maximum (der Gleichgewichtszustand) erreicht ist. Dieses Resultat macht die Problemstellen eines Raums beherrschbar, denn damit sind eine ganze Reihe potentieller Problemfälle ausgeschlossen – sie sind nicht mehr problematisch, d.h. der Ricci-Fluss verändert sie im gewünschten Sinn. Die übrig gebliebenen Problemfälle kann man nun einzeln betrachten und erfolgreich behandeln.
Perelmans Arbeit ist sehr bedeutsam für die Untersuchung der dreidimensionalen Räume. Sie ist ein wahres Meisterstück eines sehr begabten Mathematikers, der alle Ehrungen und Preisgelder für seine Entdeckung in den Wind schlug – eine geniale Arbeit spricht eben auch so für sich selbst.

Wie sieht es nun mit der topologischen Klassifizierung höherdimensionaler Räume aus? Kann man z.B. die vierdimensionalen Räume in topologische Gruppen aufteilen? Gilt auch in höheren Dimensionen die Poincaré-Vermutung?
Die vierdimensionale Poincaré-Vermutung wurde bereits im Jahr 1982 durch den Mathematiker Freedman bewiesen – er erhielt 1986 dafür die Fields-Medallie (das ist gleichsam der Mathematik-Nobelpreis). Die fünfdimensionale Poincaré-Vermutung war schon 21 Jahre früher (also 1961) von Zeeman bewiesen worden. Ein Jahr später (1962) bewies Stallings die sechsdimensionale Vermutung, und auch 1961 wurde die Vermutung für alle Räume ab sieben Dimensionen von Smale bewiesen. Der eindimensionale Fall ist sowieso trivial, und der zweidimensionale Fall ist seit mehr als 100 Jahren gelöst, wie wir weiter oben bereits gesehen hatten. Damit war seit 1982 die Poincaré-Vermutung für alle Raumdimensionen außer drei bewiesen. Perelman konnte diese Lücke 2002 schließen.
Die Poincaré-Vermutung konnte also in den höherdimensionalen Fällen (4D und mehr) schon vorher erfolgreich bewiesen werden. Konnten ebenso erfolgreich alle möglichen höherdimensionalen Räume topologisch klassifiziert werden?
Seit 1958 weiß man, dass es in vier oder mehr Dimensionen keine Hoffnung
auf eine solche vollständige Klassifizierung gibt.
A.A.Markov bewies nämlich, dass es keinen solchen Klassifizierungsalgorithmus
für vier und mehr Dimensionen geben kann
(A.A.Markov., Doklady, 121 (1958), 218-220 und
Doklady, 123 (1958), 978-980).
Offenbar gibt es
immer wieder neue Strukturen, die von den bereits verwendeten topologischen Methoden
nicht erkannt werden können – ein schönes Beispiel für
nicht-entscheidbare Probleme, denn die Frage "sind diese zwei n-dimensionalen Räume (mit
Auch die Topologie, d.h. die Lehre von der großräumigen Gestalt von Räumen, kennt also unentscheidbare Probleme (zur Erinnerung: Unentscheidbar heißt hier, dass es kein universelles Verfahren gibt, mit dem sich alle betrachteten Räume eindeutig topologisch klassifizieren lassen).
Es ist sogar so, dass man in fünf und mehr Dimensionen nicht mehr allgemein entscheiden kann, ob sich ein Raum zur entsprechenden Sphäre kontinuierlich deformieren lässt oder nicht (bewiesen durch S.P. Novikov). Man sagt, in fünf und mehr Dimensionen lassen sich sphärenartige Räume nicht mehr allgemein erkennen.
Dennoch kann man natürlich viel über die Strukturen höherdimensionaler Räume lernen – gerade in vier Dimensionen ist man zur Zeit besonders aktiv, denn vierdimensionale Räume scheinen spezielle Eigenschaften zu haben, die weder in mehr noch in weniger Dimensionen auftreten.
Die Tatsache, dass man ab vier Dimensionen die Räume nicht mehr nach ihrer großräumigen Gestalt systematisch klassifizieren kann, macht deutlich, dass auch die Poincaré-Vermutung nicht unbedingt zu den entscheidbaren Problemen gehören musste. Es wäre denkbar gewesen, dass sich die Vermutung weder beweisen noch widerlegen lässt – ganz im Sinne Gödels. Die Arbeiten von Perelman haben dann gezeigt, dass die Poincaré-Vermutung doch positiv entscheidbar ist. In diesem Fall hat man also noch einmal Glück gehabt.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 07 April 2023