Wir haben uns im letzten Kapitel mit der sogenannten nichtrelativistischen Mechanik befasst. Andere Bezeichnungen dafür sind Newtonsche Mechanik oder auch klassische Mechanik. Dabei sind wir anders als in typischen Physiklehrbüchern üblich vorgegangen.
Wir haben zunächst den Impuls eines Teilchens über eine Messvorschrift definiert und dabei die Impulserhaltung bei Teilchenkollisionen gefordert. Dann haben wir uns sehr allgemein mit Raum-Zeit-Symmetrien befasst, die eine geradlinig-gleichförmige Bewegung wieder in eine solche Bewegung überführen. Diese Raum-Zeit-Symmetrien werden mathematisch durch die affinen Abbildungen der Raum-Zeit dargestellt, wie wir gesehen haben.
Anschließend haben wir diese Raum-Zeit-Symmetrien durch eine Zusatzforderung weiter eingeschränkt. Wir haben gefordert, dass Zeitintervalle durch die Transformation nicht verändert werden dürfen. Dem entspricht die anschauliche Vorstellung, dass die Zeit universell vorgegeben ist und immer und überall in gleicher Weise abläuft. Auf diese Weise sind wir zu den (verallgemeinerten) Galilei-Transformationen gekommen, die die sogenannte Galileigruppe bilden. Wir haben weiterhin gesehen, dass sich Geschwindigkeiten unter Galileitransformationen vektoriell addieren. Die Geschwindigkeit eines Spielzeugautos, das sich in einem fahrenden Zug bewegt, ist gleich der Summe aus Zuggeschwindigkeit und der Geschwindigkeit des Spielzeugautos relativ zum Zug.
Nun haben wir gefordert, dass die Impulserhaltung mit den Galileitransformationen verträglich ist. Geht man also von den Impulsen eines physikalisch möglichen Teilchenzusammenstoßes aus, und berechnet aus diesen Impulsen über eine Galilei-Transformation neue Impulse, so gehören diese neuen Impulse ebenfalls zu einem physikalisch möglichen Zusammenstoß. Dem entspricht die anschauliche Vorstellung, dass man beispielsweise einen bestimmten Teilchenzusammenstoß (mit gleichem Ablenkwinkel etc.) einmal in einem ruhenden Zug und einmal in einem fahrenden Zug ausführen kann, und dass die Impulse der Teilchen bei diesen beiden Zusammenstößen sich über eine Galileitransformation ineinander umrechnen lassen.
Damit Galilei-Transformationen und die Impulserhaltung miteinander verträglich sind, muss ein bestimmter Zusammenhang zwischen Impuls und Geschwindigkeit der Teilchen gelten. Wir konnten ausrechnen, dass dieser Zusammenhang bei einem Teilchen mit NUmmer \(i\) durch die Formel \[ \boldsymbol{p} = m_i \boldsymbol{v} \] gegeben ist. Dabei ist \(m_i\) eine teilchenspezifische Konstante, die wir als Masse des Teilchens bezeichnet haben.
Zusätzlich haben wir gefunden, dass die Masse sich bei Zusammenstößen und Zerfällen additiv verhält. Wenn also ein Teilchen in zwei andere Teilchen zerplatzt, so ist die Summe dieser Teilchenmassen gleich der Masse des zerplatzten Teilchens.
Bei der Betrachtung der sogenannte elastischen Stöße sind wir auf eine weitere Erhaltungsgröße gestoßen: der kinetischen Energie, die durch die Formel \[ h_i(p^2) = \frac{A}{m_i} p^2 + B_i \] gegeben ist. Bei elastischen Stößen ist die Summe der kinetischen Teilchenenergien eine Erhaltungsgröße.
Zu guter letzt sind wir auf den Kraftbegriff eingegangen und haben Kraft und Impuls über die Beziehung \[ \frac{d}{dt} \boldsymbol{p} = \boldsymbol{F} \] miteinander verknüpft.
Ferner haben wir gesehen, dass Kräfte, die vom Abstand zweier Teilchen abhängen, eine weitere Einschränkung an die Galileitransformationen bewirken. Die Galileitransformation darf neben zeitlichen nun auch räumliche Abstände nicht mehr verändern. Das sind dann auch genau die Transformationen, die man in der physikalischen Literatur als Galileitransformationen bezeichnet.
Diese Vorgehensweise mag Ihnen vermutlich an vielen Stellen etwas pedantisch erschienen sein. Wir haben viele scheinbare Selbstverständlichkeiten mühsam bewiesen, und man kann durchaus die Frage stellen, ob das alles wirklich sein muss.
Die alles entscheidende Frage lautet: bestätigen die physikalischen Beobachtungen das, was wir hergeleitet haben? Verhält sich die Natur tatsächlich so, wie wir es uns überlegt haben?
Auf den ersten Blick ist das tatsächlich der Fall. Wer zweifelt schon daran, dass wenn ich zwei ein-Kilogramm-schwere Kugeln zusammenklebe, dieses Objekt dann zwei Kilogramm wiegt? Wer bezweifelt, dass die Zeit in einem fahrenden Zug dieselbe ist wie die auf dem Bahnhof? Wer bezweifelt, dass sich Geschwindigkeiten addieren und dass man zeitliche und räumliche Abstände nicht ändern darf, wenn man die Physik nicht verfälschen will?
Und dennoch: schauen wir uns die Experimente genau an!
Bei den typischen Geschwindigkeiten, die in unserer Alltagswelt auftreten, scheint es keine Probleme zu geben. Aber wenn man sich weiter umsieht, findet man auch folgende Phänomene:

Wir haben also allen Grund, anzunehmen, dass unsere bisherigen Überlegungen keineswegs eine allumfassende Gültigkeit besitzen. Sie sind vermutlich eher eine plausible Annäherung an die wirkliche physikalische Welt und haben daher nur in einem bestimmten Teilbereich der Wirklichkeit näherungsweise Gültigkeit.
Was müssen wir also tun, um zu einer besseren Beschreibung der Natur zu gelangen?
Verfolgen wir noch einmal unsere Argumentationskette:
Da ist zunächst die Idee, Teilchen durch Punkte im dreidimensionalen Raum darzustellen und ihnen eine Geschwindigkeit und einen Impuls zuzuordnen. Daran wollen wir weiterhin festhalten, da es bisher keinen Grund gibt, davon abzuweichen (später werden wir noch Gründe finden, die uns auch hier schon zu einer Änderung zwingen werden – Stichwort Quantenmechanik).
Für den Impuls haben wir eine Messvorschrift über die Idee der Impulserhaltung festgelegt. Auch daran halten wir weiterhin fest. Für alle Teilchen, die sich auch in Ruhe aufhalten können, wollen wir weiterhin einen eindeutigen Zusammenhang zwischen Impuls und Geschwindigkeit annehmen.
Ferner wollen wir wieder annehmen, dass die Impulserhaltung verträglich ist mit Raum-Zeit-Transformationen, die geradlinig-gleichförmige Bewegungen wieder in solche Bewegungen umwandeln (also mit affinen Abbildungen von Raum und Zeit).
Soweit wollen wir also dem bisherigen Rahmen treu bleiben. Doch nun kommt die entscheidende Änderung:
Wir wollen nicht mehr fordern, dass die Raum-Zeit-Transformationen Zeitintervalle unverändert lassen müssen.
Wenn wir das nämlich weiterhin fordern würden, so hätten wir wieder die Galileitransformationen mit all ihren Konsequenzen vor uns. Und diese Konsequenzen treffen in der Natur offenbar nur eingeschränkt zu.
Wir müssen also nach einer anderen Möglichkeit suchen, die Menge der möglichen affinen Raum-Zeit-Transformationen so einzuschränken, dass sie verträglich mit den physikalischen Gesetzen werden.
Betrachten wir dazu noch einmal die Beobachtungen, die wir oben in der Auflistung gemacht haben:
Es gibt Teilchen, die sich immer mit der gleichen Geschwindigkeit bewegen, egal, ob man die Messaparatur und die Quelle bewegt oder nicht. Diese Geschwindigkeit ist eine universelle Naturkonstante: die Lichtgeschwindigkeit (abgekürzt durch den Buchstaben \(c\)). Führt man diesen Teilchen Energie zu und versucht sie, zu beschleunigen, so werden sie nicht schneller! Wir wollen diese Teilchen als masselose Teilchen bezeichnen, wobei wir diese Bezeichnung erst später rechtfertigen können.
Betrachten wir nun einen Prozess, bei dem solche masselosen Teilchen auftreten:
In großen Beschleunigern kann man heute ein bestimmtes Teilchen erzeugen: das neutrale Pion. Das neutrale Pion besitzt eine Masse und kann demnach auch in unbewegten Zustand existieren. Es zerfällt nach sehr kurzer Zeit in zwei masselose Teilchen (zwei Photonen).
Zerfällt ein unbewegtes Pion, so fliegen die beiden Photonen in entgegengesetzten Richtungen mit einander gleichem Impulsbetrag auseinander. Ihre Geschwindigkeit ist gleich der Lichtgeschwindigkeit \(c\).
Zerfällt ein bewegtes Pion, so fliegen die beiden Photonen
in bestimmte Richtungen auseinander, und zwar gerade so, dass
die Impulserhaltung erfüllt ist. Dennoch ist der Betrag der Geschwindigkeit,
mit der sich die Photonen bewegen, wieder gleich der Lichtgeschwindigkeit!
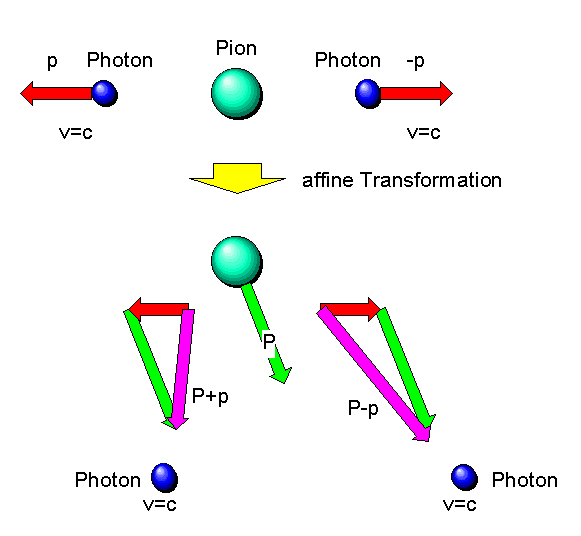
Wir suchen nun nach affinen Raum-Zeit-Transformationen, die den Zerfall des unbewegten Pions in den Zerfall des bewegten Pions überführen, so dass alle Geschwindigkeiten und Impulse korrekt ineinander umgerechnet werden.
Eine Galileitransformation schafft das nicht, denn sie könnte nicht dem Pion eine Geschwindigkeit verleihen und den Geschwindigkeitsbetrag der Photonen gleichzeitig unverändert lassen. Bei einer Galileitransformation würde zu jeder Teilchengeschwindigkeit der gleiche Geschwindigkeitsvektor \(\boldsymbol{u}\) hinzuaddiert.
Die gesuchte Raum-Zeit-Transformation muss bei masselosen Teilchen also den Betrag der Lichtgeschwindigkeit unverändert lassen.
Wir wollen diese Forderung mathematisch formulieren und sehen, was für Konsequenzen sie für die möglichen Transformationen hat.
Statt den dreidimensionalen Raum wollen wir wieder einen vierdimensionalen Raum betrachten, der die drei gewöhnlichen Raumkomponenten sowie eine Zeitkomponente umfasst. Um konsistent mit den in der Physik üblichen Schreibweisen zu sein, wollen wir allerdings die Zeitkomponente noch mit der Lichtgeschwindigkeit \(c\) multiplizieren. Das hat den Vorteil, dass sowohl die räumlichen Komponenten als auch die zeitliche Komponente die physikalische Dimension einer Länge haben. Ort \(\boldsymbol{x}\) und Zeitkomponente \(ct\) fassen wir wie früher zu einem vierdimensionalen Raumzeit-Vektor \(x\) zusammen: \[ x = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} \] wobei wir die Zeitkomponente mit dem Koordinatenindex Null versehen wollen, damit die drei Raumkomonenten ihre gewohnten Indices 1, 2 und 3 behalten können. Analog zur in der Relativitätstheorie üblichen Schreibweise werden wir die Koordinatenindices immer oben schreiben, also \[ x = \begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} \] mit \( x^0 = ct \). Solche vierdimensionalen Vektoren wollen wir auch als Vierervektoren bezeichnen.
Den vierdimensionalen Raum, in dem sich diese Vierervektoren x befinden, bezeichnen wir auch als Minkowskiraum oder Raumzeit.
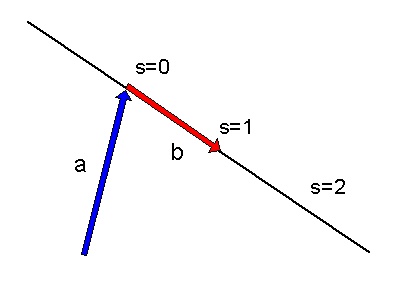
Eine geradlinig gleichförmige Bewegung wird in der vierdimensionalen
Raumzeit durch eine Gerade dargestellt. Die Punkte \(x\) der Gerade können durch
eine Funktion der Form
\[
x = a + b s
\]
dargestellt werden.
Dabei sind
\(x, a, b\)
vierdimensionale Vektoren (Vierervektoren) und \(s\) ist der
reelle Kurvenparameter.
Schreibt man die zeitliche Komponente (also die obere Null-Komponente) und die räumlichen Komponenten dieser Gleichung getrennt, so erhält man \begin{align} \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} &= \begin{pmatrix} a^0 \\ \boldsymbol{a} \end{pmatrix} + \begin{pmatrix} b^0 \\ \boldsymbol{b} \end{pmatrix} \, s \\ & \\ &= \begin{pmatrix} a^0 + b^0 s \\ \boldsymbol{a} + \boldsymbol{b} s \end{pmatrix} \end{align} Betrachten wir zwei Parameterwerte \(s_1\) und \(s_2\), die zwei verschiedenen Punkten \[ x_1 = \begin{pmatrix} ct_1 \\ \boldsymbol{x}_1 \end{pmatrix} = \begin{pmatrix} a^0 + b^0 s_1 \\ \boldsymbol{a} + \boldsymbol{b} s_1 \end{pmatrix} \] \[ x_2 = \begin{pmatrix} ct_2 \\ \boldsymbol{x}_2 \end{pmatrix} = \begin{pmatrix} a^0 + b^0 s_2 \\ \boldsymbol{a} + \boldsymbol{b} s_2 \end{pmatrix} \] auf derselben Geraden entsprechen (die unten geschriebenen Indices haben hier nichts mit den Komponenten der Vektoren zu tun – diese Indices stehen nämlich oben). Wir wollen annehmen, dass \(t_2\) größer als \(t_1\) ist (d.h. so wollen wir die Nummerierung wählen). Die Geschwindigkeit ist nun gegeben durch den Bruch aus dem räumlichen Abstand dividiert durch den zeitlichen Abstand zwischen diesen beiden Raum-Zeit-Punkten: \begin{align} \boldsymbol{v} & = c \, \frac{\boldsymbol{x}_1 - \boldsymbol{x}_1}{ct_2 - ct_1} = \\ & \\ & = c \, \frac{(\boldsymbol{a} + \boldsymbol{b} s_2) - (\boldsymbol{a} + \boldsymbol{b} s_1)} {(a^0 + b^0 s_2) - (a^0 + b^0 s_1)} = \\ & \\ & = c \, \frac{\boldsymbol{b} \, (s_2 - s_1)} {b^0 \, (s_2 - s_1)} = \\ & \\ & = c \, \frac{\boldsymbol{b}} {b^0} \end{align} Die Geschwindigkeit ist also gegeben durch den Bruch aus dem räumlichen Anteil von \(b\) (also dem dreidimensionalen Vektor \(\boldsymbol{b}\)), dividiert durch den zeitlichen Anteil von \(b\) (also der nullten Komponente \(b^0\)), multipliziert mit der Lichtgeschwindigkeit \(c\).
Wir lassen nun eine affine Raum-Zeit-Transformation \(f\) der Form \[ f(x) = \Lambda x + d \] mit einer vorgegebenen reellen \(4 \times 4\)-Matrix \(\Lambda\) und einem vorgegebenen Raumzeit-Verschiebevektor \(d\) auf Raum und Zeit wirken.
Zur Schreibweise: Früher hatten wir die affinen Transformationen in Raum und Zeit geschrieben als \( g(x) = A x + c\). Den Buchstaben \(g\) wollen wir jedoch weiter unten für die sogenannte Metrik verwenden, so dass wir statt dessen den Buchstaben \(f\) für die Bezeichnung der Transformation verwenden wollen. Ebenso soll der Buchstaben \(c\) für die Lichtgeschwindigkeit reserviert werden, so dass wir statt dessen den Buchstaben \(d\) verwenden. Der griechische Buchstabe \(\Lambda\) (Lambda) wiederum hat sich in der physikalischen Literatur der Relativitätstheorie etabliert, so dass wir ihn hier ebenfalls verwenden wollen.
Aus der Geraden \( x = a + b s \) wird durch die Raumzeit-Transformation nun die Gerade \[ x' = f(x) = f(a + b s) = \] \[ = \Lambda (a + b s) + d = \] \[ = (\Lambda a + d) + \Lambda b s \] Die neue Geschwindigkeit nach der Transformation ist also gegeben durch den Bruch aus dem räumlichen Anteil von \(\Lambda b\) dividiert durch den zeitlichen Anteil von \(\Lambda b\), multipliziert mit c.
Der üblichen Schreibweise folgend wollen wir die Indices der räumlichen Komponenten eines vierdimensionalen Vektors mit lateinischen Kleinbuchstaben kennzeichnen (also mit \(i, j, k\) etc., die Werte von 1 bis 3 annehmen können). Die Komponenten der neuen Geschwindigkeit sind also gegeben durch \[ v^k = c \, \frac{(\Lambda b)^k}{(\Lambda b)^0} \] Betrachten wir nun den Fall, dass die Geschwindigkeit vor der Transformation gleich der Lichtgeschwindigkeit \(c\) ist, d.h. \[ \boldsymbol{v}^2 = c^2 \, \frac{\boldsymbol{b}^2} {(b^0)^2} = c^2 \] Für den Vierervektor \(b\) muss dann die Beziehung \((b^0)^2 = \boldsymbol{b}^2\) oder anders geschrieben \[ (b^0)^2 - \boldsymbol{b}^2 = 0 \] gelten.
Es ist hilfreich, diese Beziehung noch etwas anders zu schreiben. Dazu definieren wir die sogenannte metrische Matrix \(g\) durch \[ g = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \] Mit Hilfe dieser Matrix können wir die (nicht positiv definite) Minkowski-Metrik in der Raumzeit definieren, die wir ebenfalls mit dem Buchstaben \(g\) bezeichnen wollen (sorry für diese zweideutige Verwendung des Buchstaben \(g\), aber so langsam werden die Buchstaben knapp). Diese Metrik ordnet einem Paar \( a, b \) von Vierervektoren eine reelle Zahl zu über die Formel \[ g(a,b) = a^T \, g \, b = a^0 b^0 - \boldsymbol{a b} \] Dabei ist \( a^T \, g \, b \) das Produkt des transponierten Vierervektors \(a^T\) mit der Matrix \(g\) und dem Vierervektor \(b\). In Komponenten ausgeschrieben lautet diese Formel \[ g(a,b) = \sum_{\mu = 0}^3 \sum_{\nu = 0}^3 \, a^\mu \, b^\nu \, g_{\mu\nu} \] Dabei sind \(g_{\mu\nu}\)die Komponenten der Matrix \(g\) (Achtung: die Indices schreiben wir hier unten!). Wir verwenden hier die Konvention, griechische Indexbuchstaben zu verwenden, wenn die Indices alle Werte von 0 bis 3 annehmen können. Lateinische Indexbuchstaben wollten wir dagegen für die räumlichen Indices 1, 2 und 3 reservieren.
Warum nun dieser Aufwand mit Indices, die mal oben und mal unten erscheinen? Genauer werden wir das erst verstehen, wenn wir das Transformationsverhalten von Vierervektoren untersuchen. Für den Moment wollen wir lediglich dem Ganzen eine Bedeutung dadurch geben, dass wir festlegen wollen, wann ein Index bei einer Vierervektorkomponente unten geschrieben werden soll. Wir definieren nämlich die Schreibweise \[ a_\mu := \sum_{\nu = 0}^3 \, g_{\mu\nu} \, a^\nu \] Man bezeichnet dies auch als das Herunterziehen eines Indexes.
Da sehr häufig über mehrfach vorkommende Indices summiert werden muss, kam Albert Einstein auf die Idee, die Summensymbole einfach wegzulassen und festzulegen, dass automatisch über mehrfach vorkommende Indices zu summieren ist. Man spricht von der Einsteinschen Summenkonvention.
In dieser Schreibweise notieren wir einfach \[ g(a,b) = a^\mu b_\mu = a_\mu b^\mu \] Wir sehen, wie elegant diese Schreibweise ist, aber man muss doch immer wieder aufpassen, was man da eigentlich tut, und gelegentlich eine Rückübersetzung in die ausführliche Schreibweise vornehmen.
Wir werden uns im Folgenden mal der einen, mal der anderen Schreibweise bedienen, je nachdem, welche Schreibweise jeweils am besten die Strukturen der Formeln zur Geltung bringt.
Kehren wir nach diesem Ausflug zurück zu unserer eigentlichen Überlegung:
Die Bewegung eines Teilchens in der Raumzeit wollten wir durch die Geradengleichung \[ x = a + b s \] darstellen. Wenn sich das Teilchen mit Lichtgeschwindigkeit bewegt, muss der Vierervektor \(b\) die Beziehung \[ (b^0)^2 - \boldsymbol{b}^2 = 0 \] erfüllen. Mit Hilfe der neuen Schreibweisen können wir diese Bedingung auch so ausdrücken: \[ g(b,b) = b^T \, g \, b = b^\mu b_\mu = 0 \] Nun wenden wir eine affine Transformation auf Raum und Zeit an, so dass die neue Bewegung durch die Gerade \[ x' = (\Lambda a + d) + \Lambda b s \] dargestellt wird. Auch diese Bewegung soll wieder mit Lichtgeschwindigkeit erfolgen, d.h. der Vierervektor \(\Lambda b\) muss ebenfalls \[ g(\Lambda b, \Lambda b) = 0 \] erfüllen. Die Forderung an die Matrix \(\Lambda\) lautet also: \[ g(b,b) = 0 \; \Rightarrow \; g(\Lambda b, \Lambda b) = 0 \] Man bezeichnet Vierervektoren mit der Eigenschaft \(g(b,b) = 0\) auch als lichtartige Vierervektoren, da sie die Bewegung von Licht beschreiben, das ja mit Lichtgeschwindigkeit fliegt.
Die Matrix \(\Lambda\) muss also aus lichtartigen Vierervektoren wieder lichtartige Vierervektoren machen!
An dieser Stelle geschieht nun in manchen Physik-Lehrbüchern ein kleines Wunder: An die Stelle der obigen Forderung tritt die Forderung, dass die Matrix \(\Lambda\) die Metrik \(g\) invariant lässt, d.h. es wird \[ g(a,b) = g(\Lambda a, \Lambda b) \] für beliebige Vierervektoren \(a\) und \(b\) des Minkowskiraums gefordert.
Diese neue Forderung nach der Invarianz der Metrik geht deutlich weiter als unsere ursprüngliche Forderung für lichtartige Vierervektoren, die aus der Forderung nach Invarianz der Metrik unmittelbar folgt.
Wir werden in den nächsten Kapiteln noch genauer untersuchen, in wieweit diese neue Forderung aus der alten Forderung folgt und ob es Transformationen gibt, die zwar lichtartige Vierervektoren wieder in lichtartige Vierervektoren umwandeln, die aber die Metrik \(g\) nicht invariant lassen.
Bei meinen Recherchen zu dem Thema bin ich auf eine interessante Vorlesung von Matt Visser: Math 465: Notes on general relativity gestoßen, die es leider nicht mehr im Internet zu geben scheint. Dort hatte ich in Kapitel 2.2 folgende Erklärung dazu gefunden:
In Matrixschreibweise kann man die Bedingung \[ g(b,b) = 0 \; \Rightarrow \; g(\Lambda b, \Lambda b) = 0 \] von oben schreiben als \[ b^T \, g \, b = 0 \; \Rightarrow \; b^T \Lambda^T \, g \, \Lambda b = 0 \] Für die gesuchte Matrix \( \Lambda^T \, g \, \Lambda \) machen wir den allgemeinen Ansatz \[ \Lambda^T \, g \, \Lambda = \Omega g + h \] mit einem passenden skalaren reellen Faktor \(\Omega\) (der ggf. auch eine reellwertige Funktion von \(\Lambda\) sein darf) und einer passenden Rest-Matrix \(h\), die aber kein Vielfaches von \(g\) sein soll (denn dafür haben wir ja den ersten Term \(\Omega g\) ). Setzen wir diesen Ansatz in \(b^T \Lambda^T \, g \, \Lambda b = 0\) ein und verwenden die Voraussetzung \(b^T \, g \, b = 0\), so folgt \[ 0 = \] \[ = b^T \Lambda^T \, g \, \Lambda b = \] \[ = b^T \, (\Omega g + h) \, b = \] \[ = \Omega \, b^T \, g \, b + b^T \, h \, b = \] \[ = b^T \, h \, b \] denn der vordere Term \( \Omega \, b^T \, g \, b \) fällt wegen der Voraussetzung \(b^T \, g \, b = 0\) weg. Wir haben also \[ 0 = b^T \, h \, b \] Das muss für alle lichtartigen \(b\) gelten, d.h. die Matrix \(h\) ist entweder ein Vielfaches von \(g\) – was wir durch den Ansatz bereits ausgeschlossen haben – oder sie ist Null. Damit haben wir das Ergebnis \[ \Lambda^T \, g \, \Lambda = \Omega g \] oder anders geschrieben \[ g(\Lambda a, \Lambda b) = \Omega \, g(a,b) \] In Matt Vissers Text wird nun argumentiert, dass \(\Omega = 1\) sein muss, wenn man die Forderung stellt, dass es keine bevorzugten Inertialsysteme (Beobachter) geben soll. Klar ist: Wenn \(\Omega\) eine Konstante ist (also keine Funktion von \(\Lambda\)), so brauchen wir nur für \(\Lambda\) die Einheitsmatrix einsetzen (diese triviale Matrix muss wegen der Gruppenstruktur der Raumzeit-Transformationen auf jeden Fall erlaubt sein – sie gehört zum neutralen Element) und erhalten sofort aus der obigen Gleichung \(\Omega = 1\). Falls aber \(\Omega\) eine Funktion der Parameter der Lorentzmatrix \(\Lambda\) ist (siehe nächstes Kapitel), so folgen nach Matt Visser daraus beobachtbare Konsequenzen, die bestimmte Bezugssysteme auszeichnen. Da wir das nicht zulassen wollen, muss \(\Omega\) konstant und damit gleich \(1\) sein.
Soviel dazu – wie man sieht, ist die Diskussion keineswegs trivial und erfordert gewisse Zusatzannahmen, die über die Konstanz der Lichtgeschwindigkeit hinausgehen.
Die affinen Raum-Zeit-Transformationen \[ f(x) = \Lambda x + d \] die die Raumzeit-Metrik \(g\) invariant lassen, also \[ g(a,b) = g(\Lambda a, \Lambda b) \] erfüllen, bezeichnet man als Poincaré-Transformationen. Diese Transformationen besitzen eine Gruppenstruktur, wenn man sie nacheinander ausführt – man spricht deshalb auch von der Poincaré-Gruppe.
Die Poincaré-Transformationen umfassen einmal Verschiebungen (Translationen) in Raum und Zeit (gegeben durch den Vierervektor \(d\)) sowie spezielle lineare Transformation der Raum- und Zeitkoordinaten (gegeben durch die Matrix \(\Lambda\)), die die Metrik \(g\) invariant lassen.
Die Poincaré-Transformationen, die keine Verschiebung in Raum und Zeit bewirken (also \(d = 0\) ), werden auch als Lorentz-Transformationen bezeichnet, wobei die Menge der Lorentz-Transformationen die Lorentz-Gruppe bildet. Wir werden uns in einem der nächsten Abschnitte die Lorentz-Transformationen noch genauer ansehen und uns fragen, welche physikalischen Konsequenzen sich daraus ergeben.
© Jörg Resag, www.joerg-resag.de
last modified on 21 June 2023