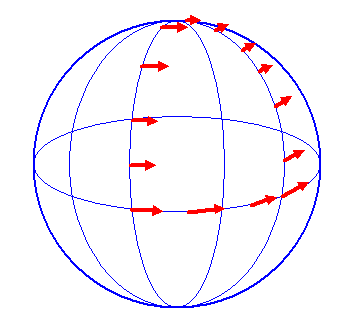
In den letzten beiden Kapiteln haben wir Tangentialvektorfelder und Co-Tangentialvektorfelder auf Mannigfaltigkeiten kennengelernt – beides Strukturen, die sich beispielsweise über die Richtungsableitung skalarer Funktionen entlang von Kurven unmittelbar auf differenzierbaren Mannigfaltigkeiten definieren lassen.
Wir wollen uns in diesem Kapitel nun Ableitungen von Tangentialvektorfeldern anschauen. Eine Möglichkeit, das zu tun, besteht darin, eine weitere Struktur auf der Mannigfaltigkeit zu definieren, die als kovariante Ableitung oder auch als affiner Zusammenhang bezeichnet wird (eine andere Möglichkeit ist die sogenannte Lie-Ableitung, die ein Vektorfeld und den dadurch generierten Fluss voraussetzt – Details kommen in einem späteren Kapitel). Die Einführung dieser affinen Struktur bewirkt, dass man von differenzierbaren Mannigfaltigkeiten zur sogenannten affinen Geometrie auf diesen Mannigfaltigkeiten übergeht. Es wird nämlich möglich werden, beispielsweise von einer möglichst geraden Kurve (einer geodätischen Linie) zu sprechen.
Wie verändert sich nun also ein Tangentialvektorfeld, wenn wir uns auf einer Mannigfaltigkeit in eine bestimmte Richtung (gegeben durch eine Kurve) bewegen?
Wir werden feststellen, dass die naive Ableitung eines Tangentialvektorfeldes in einer bestimmten Richtung in einem Punkt \(p\) im Allgemeinen keinen Tangentialvektor in \(p\) ergibt. Veranschaulichen wir uns die Situation durch zweidimensionale Flächen, eingebettet im dreidimensionalen Raum, so besitzt die naive Ableitung eines Tangentialvektorfeldes im dreidimensionalen Raum auch eine Komponente senkrecht zur Fläche. Diese senkrechte Komponente ist darauf zurückzuführen, dass sich die Fläche krümmt und sich das Tangentialvektorfeld eben nicht nur parallel zur Fläche ändert, sondern auch senkrecht dazu, wenn man sich ein kleines Stück auf der Fläche fortbewegt. Nur so kann das Tangentialvektorfeld tangential zur gekrümmten Fläche bleiben.
Möchte man auf eine Einbettung verzichten, so stört die Komponente senkrecht zur Fläche, denn sie ist zunächst gar nicht definiert. Man definiert daher die sogenannte kovariante Ableitung, bei der man einfach die senkrechte Änderungskomponente weglässt. Man projeziert also gleichsam den Ableitungsvektor auf den Tangentialraum, so dass der kovariante Ableitungsvektor selbst ein Element des Tangentialraums ist. Diese Vorgehensweise kann man dann leicht auf allgemeine differenzierbare Mannigfaltigkeiten ohne Einbettung verallgemeinern.
Einen Punkt muss man jedoch bedenken: Da wir die Änderungskomponente senkrecht zur Fläche weggelassen haben, liefert die kovariante Ableitung nicht mehr in linearer Näherung die Veränderung des Tangentialvektorfeldes mit Formeln wie \[ u(\gamma(dt)) = u(p) + D_{\gamma'(0)} \, u(p) \, dt \] mit \( \gamma(0) = p \) und der kovarianten Ableitung \(D_{\gamma'(0)} \, u(p) \) in \(\gamma'(0)\)-Richtung. Man muss sich daher etwas anderes überlegen, um benachbarte Tangentialvektoren über die kovariante Ableitung miteinander in Beziehung zu setzen. Das Zauberwort heißt Paralleltransport (Parallelverschiebung) – wir werden weiter unten genauer darauf eingehen.
Wir wollen die obigen Ideen nun präzisieren. Dabei betrachten wir zunächst zweidimensionale gekrümmte Flächen, eingebettet im dreidimensionalen euklidischen Raum, um eine anschauliche Vorstellung der auftretenden mathematischen Ausdrücke zu ermöglichen.
Wiederholen wir kurz ein Ergebnis aus Kapitel 4 über Tangentialvektoren: Einen Punkt \(p\) unserer zweidimensionalen Fläche \(M\) können wir aufgrund der Einbettung als einen dreidimensionalen Vektor \(\boldsymbol{X}(x)\) im Einbettungsraum \(\mathbb{R}^{3}\) darstellen. Dabei liefert \( x = (x^{1}, x^{2}) \) die beiden Koordinaten des Punktes \(p\), d.h. \( x = f(p) \) mit der Koordinatenfunktion (Karte) \(f\). Man sagt auch, \(\boldsymbol{X}(x)\) liefert eine Parametrisierung der Fläche \(M\) im Einbettungsraum \(\mathbb{R}^{3}\). Wegen \( p = \boldsymbol{X}(x) \) und \( x = f(p) \) ist \( \boldsymbol{X} \) die Umkehrfunktion zur Koordinatenfunktion \(f\), d.h. \[ p = \boldsymbol{X}(x) = f^{-1}(x) \] Ein Beispiel:
\(M\) ist die Kugeloberfläche einer Kugel mit Radius 1, und \[ x^{1} = \theta \] \[ x^{2} = \varphi \] sind die Kugelkoordinatenwinkel, analog zu Längen- und Breitengrad auf der Erde. In den euklidischen Koordinaten des umgebenden dreidimensionalen Einbettungsraums ist dann \[ \boldsymbol{X}(\theta, \varphi) = \begin{pmatrix} \sin{\theta} \, \cos{\varphi} \\ \sin{\theta} \, \sin{\varphi} \\ \cos{\theta} \end{pmatrix} \] Der Winkel \(\varphi\) wächst also von Westen nach Osten von \(0\) bis \(2\pi\) (also bis 360 Grad) an, der Winkel \(\theta\) dagegen von Norden nach Süden von \(0\) bis \(\pi\) (also bis 180 Grad).
Einen Tangentialvektor \(u(p)\) können wir aufgrund der Einbettung nun schreiben als \[ u(p) = \sum_{\mu} \, u^{\mu}(p) \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \] mit \( x = f(p) \). Der Vektor \(u(p)\) ist demnach ein dreidimensionaler Vektor, der in \(p\) tangential zur Fläche \(M\) liegt. In der Summe läuft der Koordinatenindex \(\mu\) von 1 bis 2.
Wir betrachten nun wie üblich eine Kurve \( \gamma(t) \) mit \( \gamma(0) = p \). Dabei muss \(u(p)\) hier nicht tangential zu dieser Kurve liegen, d.h. \(\gamma\) ist hier nicht dieselbe Kurve, die \(u(p)\) definiert. Vielmehr soll \( \gamma(t) \) die Kurve sein, in deren Richtung wir die Änderung von \(u\) betrachten wollen.
Wir interessieren uns also nun für die Änderung von \( u(\gamma(t)) \) bei \( t = 0 \) in \(\gamma\)-Kurvenrichtung. Da \( u(\gamma(t)) \) für jedes \(t\) im Einbettungsraum ein dreidimensionaler Vektor ist, ist auch die Ableitung nach \(t\) in \( t = 0 \) unmittelbar definiert.
Ohne Einbettung wäre diese naive Ableitung dagegen erst einmal nicht definiert, da formal im Differenzenquotienten der Ableitung die Differenz zweier Tangentialvektoren aus verschiedenen Tangentialräumen auftritt, die nur bei einer Einbettung eine unmittelbar klare Bedeutung hat.
Rechnen wir die Ableitung also jetzt aus, wobei wir benutzen, dass \( f(\gamma(0)) = f(p) = x \) ist: \[ \frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} = \] \[ = \frac{d}{dt} \, \sum_{\mu} \, u^{\mu}(\gamma(t)) \, \frac{\partial \boldsymbol{X}(f(\gamma(t)))}{\partial x^{\mu}} \bigg|_{t = 0} = \] \[ = \sum_{\mu} \, \frac{d}{dt} u^{\mu}(\gamma(t)) \bigg|_{t = 0} \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} + \] \[ + \sum_{\mu} \, u^{\mu}(p) \, \frac{d}{dt} \frac{\partial \boldsymbol{X}(f(\gamma(t))}{\partial x^{\mu}} \bigg|_{t = 0} = \] \[ = \sum_{\mu} \, \frac{d}{dt} u^{\mu}(\gamma(t)) \bigg|_{t = 0} \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} + \] \[ + \sum_{\mu \nu} \, u^{\mu}(p) \, \frac{\partial}{\partial x^{\nu}} \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \frac{d}{dt} f(\gamma(t))^{\nu} \bigg|_{t = 0} \] Der erste Term beschreibt die Veränderung aufgrund der Änderung \[ \frac{d}{dt} u^{\mu}(\gamma(t)) \bigg|_{t = 0} \] der Vektor-Komponenten \( u^{\mu}(\gamma(t)) \) in Kurvenrichtung, und der zweite Term enthält die Veränderung \[ \frac{\partial}{\partial x^{\nu}} \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \] der Tangential-Basisvektoren \( \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \) in \(\nu\)-Koordinatenrichtung aufgrund der Veränderung der Koodinatenlinien-Richtungen im Einbettungsraum. Wegen der Einbettung ist diese Veränderung des \(\mu\)-ten Basisvektors (d.h. \(\mu\) fest) in \(x^{\nu}\)-Koordinatenrichtung ein dreidimensionaler Vektor, den wir nach drei Basisvektoren in \(\mathbb{R}^{3}\) entwickeln können. Im Punkt \(p\) sind solche Basisvektoren gegeben durch die beiden Tangentialvektoren \( \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}} \) (mit \(\rho\) gleich 1 und 2) sowie dem dazu senkrechten Vektor \(\boldsymbol{N}\), der im Punkt \(p\) senkrecht zur eingebetteten Fläche steht. Wir können also schreiben: \[ \frac{\partial}{\partial x^{\nu}} \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} =: \] \[ =: \sum_{\rho} \, \Gamma^{\rho}_{\nu\mu} \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}} + h_{\nu\mu} \boldsymbol{N} \] Durch diese Gleichung werden die Christoffel-Symbole \( \Gamma^{\rho}_{\nu\mu} \) definiert (wir verwenden die Konvention, dass der Index, nach dem abgeleitet wird, vorne steht). Die obige Gleichung zeigt, dass sie die folgende anschauliche Bedeutung haben:
|
Christoffel-Symbole: Das Christoffel-Symbol \( \Gamma^{\rho}_{\nu\mu} \) ist die \(\rho\)-te Komponente (bezogen auf die koordinatenabhängige Basis \( \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}} \) des Tangentialraums) des Vektors \[ \frac{\partial}{\partial x^{\nu}} \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \] der die Änderung des \(\mu\)-ten Basis-Tangentialvektors \( \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \) in \(x^{\nu}\)-Koordinatenrichtung angibt.
|
Das können wir nun verwenden, um die obige Rechnung weiterzuführen.
Außerdem wollen wir noch \( \gamma'(0) =: v(p) \) schreiben, d.h.
\[
\frac{d}{dt} f(\gamma(t))^{\nu} \bigg|_{t = 0} =
v^{\nu}(p)
\]
Damit erhalten wir (wir wiederholen dabei nochmal die Gleichung von oben):
\[
\frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} =
\]
\[
= \sum_{\mu} \,
\frac{d}{dt} u^{\mu}(\gamma(t)) \bigg|_{t = 0} \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}}
+
\]
\[ +
\sum_{\mu \nu} \,
u^{\mu}(p) \, \frac{\partial}{\partial x^{\nu}}
\frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}}
\frac{d}{dt} f(\gamma(t))^{\nu} \bigg|_{t = 0} = \, ...
\]
... jetzt kommt das Einsetzen im zweiten Term:
\[
= \sum_{\mu} \,
\frac{d}{dt} u^{\mu}(\gamma(t)) \bigg|_{t = 0} \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}}
+
\]
\[ +
\sum_{\mu \nu} \,
u^{\mu}(p) \,
\left(
\sum_{\rho} \, \Gamma^{\rho}_{\nu\mu}
\frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}}
+ h_{\nu\mu} \boldsymbol{N}
\right) \, v^{\nu}(p) =
\]
... wir bennen im ersten Term den Index \(\mu\) um in \(\rho\)
und ziehen die Summe über \(\rho\) nach vorne,
sodass wir den Basisvektor \( \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}} \) ausklammern können:
\[
= \sum_{\rho} \, \bigg(
\frac{d}{dt} u^{\rho}(\gamma(t)) \bigg|_{t = 0} +
\]
\[
+
\sum_{\mu\nu} \,
u^{\mu}(p) \, \Gamma^{\rho}_{\nu\mu}
\, v^{\nu}(p)
\bigg) \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}}
+
\]
\[
+
\sum_{\mu\nu} \,
u^{\mu}(p) \, h_{\nu\mu} \boldsymbol{N}
\, v^{\nu}(p)
\]
Soweit also unser Ergebnis zu
\( \frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} \)
(also die Änderung des Tangentialvektors \(u\) in Kurvenrichtung bei Einbettung der Fläche).
Das Ergebnis enthält drei Anteile:
Oben hatten wir bereits erwähnt, dass die Änderung der Basisvektoren senkrecht zum Tangentialraum stört, wenn man ohne eine Einbettung auskommen will. Ohne eine Einbettung ist \( \frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} \) gar nicht definiert.
Wenn wir aber die Komponente senkrecht zum Tangentialraum weglassen, so lassen sich die übrigen Terme problemlos einbettungsfrei umschreiben. Das verwundert auch nicht, denn die Projektion von \( \frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} \) auf den Tangentialraum in \(p\) is ja selbst ein Element dieses Tangentialraums. Wir definieren daher die kovariante Ableitung wie folgt:
|
Definition der kovarianten Ableitung auf einer zweidimensionalen Fläche,
eingebettet im dreidimensionalen euklidischen Raum: Die kovariante Ableitung \( D_{v(p)} u \) eines Tangentialvektorfeldes \(u\) im Punkt \(p\) in Richtung des Tangentialvektors \(v(p) = \gamma'(0)\) (festgelegt durch die oben angegebene Kurve \(\gamma(t)\)) ist die Projektion von \( \frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} \) auf den Tangentialraum in \(p = \gamma(0)\). Wir schreiben das als \[ D_{v(p)} u := P|_{T(p)} \frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} \] mit dem linearen Projektionsoperator \(P|_{T(p)}\) auf den Tangentialraum \(T(p)\). Bezogen auf die Basisvektoren \( \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}} \) des Tangentialraums gilt: \[ D_{v(p)} u = \] \[ = \sum_{\rho} \, \bigg( \frac{d}{dt} u^{\rho}(\gamma(t)) \bigg|_{t = 0} + \] \[ + \sum_{\mu\nu} \, u^{\mu}(p) \, \Gamma^{\rho}_{\nu\mu} \, v^{\nu}(p) \bigg) \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}} \] Dabei sind die Christoffelsymbole \( \Gamma^{\rho}_{\nu\mu} \) definiert durch \[ P|_{T(p)} \frac{\partial}{\partial x^{\nu}} \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} =: \sum_{\rho} \, \Gamma^{\rho}_{\nu\mu} \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}} \] d.h. der Term mit dem Normalenvektor \(\boldsymbol{N}\) entfällt wegen dem vorgeschalteten Projektionsoperator \(P|_{T(p)}\).
|
Man kann für die Christoffelsymbole noch eine etwas griffigere Formel ableiten,
indem man in \( D_{v(p)} u \) für
\(u(p)\) den Basisvektor \( \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \)
und für \(v(p)\) den Basisvektor
\( \frac{\partial \boldsymbol{X}(x)}{\partial x^{\nu}} \)
einsetzt. Die Laufindizes in der Summe erhalten zur Unterscheidung dann einen Strich.
Es ist dann \( u^{\mu'}(p) = \delta^{\mu'\mu} \) und
\( v^{\nu '}(p) = \delta^{\nu '\nu} \),
so dass in den Summen über \(\mu'\) und \(\nu'\) jeweils nur ein Term übrig bleibt.
Die Zeitableitung \( \frac{d}{dt} u^{\rho}(\gamma(t)) \big|_{t = 0} \)
fällt weg, da \( u^{\rho}(p) = \delta^{\rho\mu} \) konstant ist:
\[
D_{\frac{\partial \boldsymbol{X}(x)}{\partial x^{\nu}}}
\frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} =
\]
\[
=
\sum_{\rho} \, \bigg(
\frac{d}{dt} u^{\rho}(\gamma(t)) \bigg|_{t = 0}
+
\]
\[
\sum_{\mu' \nu'}
u^{\mu'}(p) \, \Gamma^{\rho}_{\nu' \mu'}
v^{\nu '}(p) \bigg)
\frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}}
=
\]
\[
=
\sum_{\rho} \,
\Gamma^{\rho}_{\nu\mu}
\, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}}
\]
Der Vergleich mit der Formel
\[
\frac{\partial}{\partial x^{\nu}} \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}}
\]
\[
=:
\sum_{\rho} \, \Gamma^{\rho}_{\nu\mu}
\frac{\partial \boldsymbol{X}(x)}{\partial x^{\rho}}
+ h_{\nu\mu} \boldsymbol{N}
\]
etwas weiter oben für die Christoffelsymbole zeigt,
dass für den Operator der kovarianten Ableitung
\( D_{\frac{\partial \boldsymbol{X}(x)}{\partial x^{\nu}}} \)
gilt:
\[
D_{\frac{\partial \boldsymbol{X}(x)}{\partial x^{\nu}}}
=
P|_{T(p)} \frac{\partial}{\partial x^{\nu}}
\]
denn der Projektionsoperator \(P|_{T(p)}\) löscht den
\(\boldsymbol{N}\)-Anteil.
Dieser Ausdruck ist allerdings nur bei einer Einbettung definiert.
Er zeigt aber sehr schön, was die kovariante Ableitung macht:
\( D_{\frac{\partial \boldsymbol{X}(x)}{\partial x^{\nu}}} \)
ermittelt die Veränderung eines Tangentialvektors in
\(x^\nu\)-Koordinatenrichtung, wobei dieser Veränderungsvektor
noch auf den Tangentialraum projeziert wird.
Nachdem wir uns nun eine anschauliche Vorstellung von der kovarianten Ableitung verschafft haben, wollen wir nun versuchen, diesen Begriff auf die einbettungsfreie Formulierung zu übertragen. Die Tangentialvektoren werden dabei durch Richtungsableitungen dargestellt, was im Wesentlichen bedeutet, dass man formal in Ausdrücken wie \[ u(p) = \sum_{\mu} \, u^{\mu}(p) \, \frac{\partial \boldsymbol{X}(x)}{\partial x^{\mu}} \] das \( \boldsymbol{X}(x) \) weglässt und so zu den Richtungsableitungen \[ u(p) = \sum_{\mu} \, u^{\mu}(p) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] übergeht. Entsprechend könnte man die kovariante Ableitung in Analogie zu oben direkt einbettungsfrei über die folgenden Formeln definieren:
|
einbettungsfreie Definition der kovarianten Ableitung: Die kovariante Ableitung \( D_{v(p)} u \) eines Tangentialvektors \(u(p)\) in Richtung des Tangentialvektors \(v(p)\) (wobei \(v(p)\) Tangentialvektor zur Kurve \( \gamma(t) \) mit \(p = \gamma(0)\) ist) definieren wir als \[ D_{v(p)} u = \sum_{\rho} \, \bigg( v(p) \, u^{\rho} \, + \] \[ + \sum_{\mu \nu} \, u^{\mu}(p) \, \Gamma^{\rho}_{\nu\mu} \, v^{\nu}(p) \bigg) \, \frac{\partial}{\partial x^{\rho}} \bigg|_{p} \] wobei wir im ersten Term \[ \frac{d}{dt} u^{\rho}(\gamma(t)) \bigg|_{t = 0} = v(p) \, u^{\rho} \] verwendet haben. Dabei sind die Christoffelsymbole \( \Gamma^{\rho}_{\nu\mu} \) definiert durch \[ D_{\frac{\partial}{\partial x^{\nu}}\big|_{p}} \, \frac{\partial}{\partial x^{\mu}} = \sum_{\rho} \, \Gamma^{\rho}_{\nu\mu} \, \frac{\partial}{\partial x^{\rho}} \bigg|_{p} \]
|
Auf diese Weise wird beispielsweise in der physikalischen Literatur
die kovariante Abbildung häufig definiert. Dabei muss man die Christoffelsymbole
vorgeben oder aufgrund anderer Prinzipien festlegen.
Unsere obigen Überlegungen haben gezeigt, dass beispielsweise
bei einer Einbettung die Christoffelsymbole eindeutig festgelegt sind.
Analog ist es, wenn eine Metrik auf der Mannigfaltigkeit vorliegt (siehe ein späteres Kapitel).
Noch eine wichtige Randbemerkung: Leitet man die Christoffelsymbole wie oben gezeigt aus einer Einbettung ab (man spricht davon, dass die Einbettung den affinen Zusammenhang induziert), so sind die Christoffelsymbole symmetrisch in den unteren beiden Indices. Bei der einbettungsfreien Formulierung haben wir dagegen die Freiheit, auch nicht-symmetrische Christoffelsymbole zuzulassen. Man spricht in diesem Fall von Torsion (siehe nächstes Kapitel).
Die obige Definition hat den Nachteil, dass man expliziten Bezug auf Koordinaten nimmt, um den koordinaten-unabhängigen Ausdruck \( D_{v(p)} u \) zu definieren. Dass \( D_{v(p)} u \) koordinatenunabhängig sein muss, ist für den Fall der Einbettung anschaulich klar, denn dort hatten wir den koordinaten-unabhängigen Ausdruck \[D_{v(p)} u := P|_{T(p)} \frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} \] als Ausgangspunkt der Rechnung gewählt. Bei der obigen einbettungsfreien Definition über Koordinaten müsste man aber die Koordinaten-Unabhängigkeit noch explizit nachweisen bzw. von den Christoffelsymbolen ein entsprechendes Transformationsverhalten verlangen.
In der mathematischen Literatur geht man daher gerne einen anderen Weg: Man definiert die kovariante Ableitung in \(v(p)\)-Richtung als Abbildung \(D_{v(p)}\), die aus einem Tangentialvektorfeld \(u\), das in einer Umgebung von \(p\) definiert sein muss, einen neuen Tangentialvektor \( D_{v(p)} u \) im Tangentailraum \(T(p)\) macht (bei der Definition über eine Einbettung ist \( D_{v(p)} u \) ja auch ein Tangentialvektor).
Von dieser Abbildung verlangt man nun eine Reihe von Eigenschaften, so wie sie auch bei der Definition über die Einbettung gegeben sind. Diese Eigenschaften müssen dann ausreichen, um den obigen koordinatenabhängigen einbettungsfreien Ausdruck für die kovariante Abbildung (also der mit den Christoffelsymbolen) reproduzieren zu können, so dass die Gleichwertigkeit zu dieser Definition gewährleistet ist. Schauen wir uns die Details an:
|
einbettungsfreie Definition der kovarianten Ableitung ohne Koordinaten: Für zwei Tangentialvektorfelder \(u\) und \(v\) ist die kovariante Ableitung von \(u\) in \(v(p)\)-Richtung in \(p\) ein Tangentialvektor des Tangentialraums \(T(p)\). Wir schreiben diesen Tangentialvektor als \( D_{v(p)} u \). Dabei sollen die folgenden Eigenschaften gelten: \( D_{v(p)} u \) ist algebraisch linear in \(v(p)\), d.h. für zwei skalare Funktionen \(\phi\) und \(\chi\) sowie ein weiteres Tangentialvektorfeld \(w\) gilt: \[ D_{\phi(p) \, v(p) + \chi(p) \, w(p)} u = \] \[ = \phi(p) \, D_{v(p)} u + \chi(p) \, D_{w(p)} u \] \(D_{v(p)} u \) ist additiv in \(u\), d.h. \[ D_{v(p)} (u + w) = \] \[ = D_{v(p)} u + D_{v(p)} w \] \( D_{v(p)} u \) genügt der Produktregel, d.h. \[ D_{v(p)} (\phi \, u) = \] \[ = \phi(p) \, D_{v(p)} u + (D_{v(p)} \phi) \, u(p) \] wobei \( D_{v(p)} \phi \) die normale Richtungsableitung von \(\phi\) in \(v(p)\)-Richtung ist, also \[ D_{v(p)} \phi := v(p) \, \phi \] Wegen dieser Richtungsableitung hängt \( D_{v(p)} u \) nicht nur von \(p\), sondern von einer Umgebung von \(p\) ab (so wie das bei Ableitungen ja sein muss – man interessiert sich ja für Veränderungen und muss daher auch etwas über die Nachbarschaft des Punktes \(p\) wissen). Daher haben wir auch in \( D_{v(p)} u \) kein \( (p) \) hinter dem \(u\) geschrieben. |
Man kann sich alle diese Regeln mit Hilfe einer Einbettung und
der dortigen Definition
\[
D_{v(p)} u := P|_{T(p)}
\frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0}
\]
plausibel machen.
Ebenso kann man verifizieren, dass diese Regeln bei der weiter oben
getroffenen koordinatenabhängigen einbettungsfreien
Definition mit Christoffelsymbolen erfüllt sind.
Wir wollen das hier überspringen.
Schauen wir umgekehrt nach, ob die Regeln ausreichen, um die koordinatenabhängige einbettungsfreie Formulierung mit Christoffelsymbolen zurückzugewinnen. Damit stellen wir sicher, dass wir keine wichtige Regel übersehen haben: \[ D_{v(p)} u = \] \[ = D_{v(p)} \, \sum_{\mu} \, u^{\mu} \frac{\partial}{\partial x^{\mu}} = \, ... \] wir verwenden die Addiditivität:
\[ = \sum_{\mu} \, D_{v(p)} \left( u^{\mu} \frac{\partial}{\partial x^{\mu}} \right) = \, ... \] wir verwenden die Produktregel:
\[
=
\sum_{\mu} \, \bigg(
(D_{v(p)}
u^{\mu}) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p}
+
\]
\[ +
u^{\mu}(p) \, D_{v(p)} \frac{\partial}{\partial x^{\mu}} \bigg)
= \, ...
\]
Im ersten Term verwenden wir, dass nach Definition
\( D_{v(p)} u^{\mu} = \) \(
v(p) \, u^{\mu}
= \) \(
\frac{d}{dt} u^{\mu}(\gamma(t)) \big|_{t = 0} \)
ist.
Im zweiten Term schreiben wir \( v(p) = \sum_{\nu} \,
v^{\nu}(p) \frac{\partial}{\partial x^{\nu}} \big|_{p} \). Ergebnis:
\[
=
\sum_{\mu} \, \bigg(
(v(p) \, u^{\mu}) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p}
+
\]
\[ +
u^{\mu}(p) \, D_{\sum_{\nu} \,
v^{\nu}(p) \frac{\partial}{\partial x^{\nu}} \big|_{p}}
\frac{\partial}{\partial x^{\mu}}
\bigg)
= \, ...
\]
wir verwenden die algebraische Linearität im zweiten Term:
\[ = \sum_{\mu} \, \bigg( (v(p) \, u^{\mu}) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} + \] \[ + u^{\mu}(p) \, \sum_{\nu} \, v^{\nu}(p) \, D_{\frac{\partial}{\partial x^{\nu}} \big|_{p}} \frac{\partial}{\partial x^{\mu}} \bigg) = \, ... \] Im zweiten Term können wir über \[ D_{\frac{\partial}{\partial x^{\nu}} \big|_{p}} \frac{\partial}{\partial x^{\mu}} =: \sum_{\rho} \, \Gamma^{\rho}_{\nu\mu} \, \frac{\partial}{\partial x^{\rho}} \bigg|_{p} \] die Christoffelsymbole einführen (eine solche Gleichung muss gelten, denn die linke Seite ist nach Definition ein Tangentialvektor, der sich nach den Basisvektoren des Tangentialraums entwickeln lassen muss):
\[ = \sum_{\mu} \, \bigg( (v(p) \, u^{\mu}) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} + \] \[ + u^{\mu}(p) \, \sum_{\nu} \, v^{\nu}(p) \, \sum_{\rho} \, \Gamma^{\rho}_{\nu\mu} \, \frac{\partial}{\partial x^{\rho}} \bigg|_{p} \bigg) = \, ... \] Umsortieren und Indexumbenennung ergibt schließlich:
\[ = \sum_{\rho} \, \bigg( v(p) \, u^{\rho} + \] \[ + \sum_{\mu\nu} \, u^{\mu}(p) \, \Gamma^{\rho}_{\nu\mu} \, v^{\nu}(p) \bigg) \, \frac{\partial}{\partial x^{\rho}} \bigg|_{p} \] Das ist genau unsere Formel von der koordinatenabhängigen Definition der kovarianten Ableitung, die wir hiermit reproduzieren konnten. Dabei haben wir genau die Regeln gebraucht, deren Gültigkeit wir oben gefordert haben. Diese Regeln reichen also aus, und wir haben keine weitere Regel benötigt.
Die kovariante Ableitung \( D_{v(p)} u \) ist also nach Definition ein Tangentialvektor, dessen Komponenten gegeben sind durch \[ D_{v(p)} u = \sum_{\rho} \, \bigg( v(p) \, u^{\rho} + \] \[ + \sum_{\mu\nu} \, u^{\mu}(p) \, \Gamma^{\rho}_{\nu\mu} \, v^{\nu}(p) \bigg) \, \frac{\partial}{\partial x^{\rho}} \bigg|_{p} \] mit den Christoffelsymbolen \( \Gamma^{\rho}_{\nu\mu} \), die durch \[ D_{\frac{\partial}{\partial x^{\nu}} \big|_{p}} \frac{\partial}{\partial x^{\mu}} =: \sum_{\rho} \, \Gamma^{\rho}_{\nu\mu} \, \frac{\partial}{\partial x^{\rho}} \bigg|_{p} \] definiert sind. Insgesamt müssen sich also die Komponenten, die durch die große Klammer definiert sind, wie die Komponenten eines Tangentialvektors bei Koordinatenwechseln transformieren. Sie transformieren sich also genauso wie die Komponenten \(u^{\mu}(p)\) und \(v^{\mu}(p)\), die in der Klammer ebenfalls vorkommen.
Als Folge davon weist das Christoffelsymbol ein komplexeres Transformationsverhalten auf, das gerade so beschaffen sein muss, dass die große Klammer das gewünschte Transformationsverhalten aufweist.
Dabei ist besonders wichtig, dass die Klammer die Richtungsableitung \( v(p) \, u^{\rho} \) von Tangentialvektorkomponenten enthält. Bei Koordinatentransformationen entstehen dadurch Zusatzterme, die durch das Transformationsverhalten der Christoffelsymbole kompensiert werden müssen.
Physiker kennen das von Eichtheorien, bei denen das Eichpotential \( A_{\mu}(x) \) die Zusatzterme von \( \partial_{\mu} \psi(x) \) bei Eichtransformationen neutralisieren muss, so dass \( D_{\mu}(A) \psi(x) \) sich bei Eichtransformationen genauso transformiert wie \( \psi(x) \) (Details siehe Quantenfeldtheorie und Eichfelder, Kapitel 6: Eichtheorien).
Analog hier: Die Komponenten von \( D_{v(p)} u \) sollen sich bei Koordinatentransformationen genauso transformieren wie die Komponenten von \(u(p)\), d.h. \( D_{v(p)} u \) soll ein Tangentialvektor sein wie \(u(p)\). Halten wir fest:
Um es konkret zu machen: Am einfachsten lässt sich das Transformationsverhalten beschreiben, wenn man die folgenden Objekte mit Hilfe der Basisvektoren des Co-Tangentialraums definiert: \[ \Theta^{\rho}_{\,\mu} := \sum_{\nu} \, \Gamma^{\rho}_{\nu\mu} \, dx^{\nu} \] \(\Theta\) ist also eine Matrix, deren Elemente Co-Tangentialvektoren sind. Die \(\nu\)-Koordinate wird durch die Bildung von \(\Theta\) gleichsam versteckt, denn \(\Theta\) enthält keine \(\mu\)-Koordinatenabhängigkeit mehr. Insbesondere ist \[ \Theta^{\rho}_{\,\mu}(p) \, v(p) = \] \[ = \sum_{\nu} \, \Gamma^{\rho}_{\nu\mu} \, dx^{\nu}|_{p} \, v(p) = \] \[ = \sum_{\nu} \, \Gamma^{\rho}_{\nu\mu} \, v^{\nu}(p) \] Damit lässt sich die kovariante Ableitung schreiben als \[ D_{v(p)} u = \sum_{\rho} \, \bigg( v(p) \, u^{\rho} + \] \[ + \sum_{\mu} \, u^{\mu}(p) \, \Theta^{\rho}_{\,\mu}(p) \, v(p) \bigg) \, \frac{\partial}{\partial x^{\rho}} \bigg|_{p} \] Als Spaltenvektor gesehen ist \( D_{v(p)} u \) also gegeben durch \( v(p) \, u + \Theta(v) \, u(p) \), wobei der Spaltenvektor \( v(p) \, u \) die Komponenten \( v(p) \, u^{\rho} \)hat und \( \Theta(v) \) als Matrix mit Komponenten \( \Theta^{\rho}_{\,\mu}(p) \, v(p) \) zu lesen ist. Die Matrix \( \Theta(v) \) wird dabei mit dem Spaltenvektor \(u(p)\) multipliziert.
Geht man nun von Koordinaten \(x\) zu Koordinaten \(x'\) über mit der Jacobi-Matrix \[ J^{\lambda}_{\mu} := \frac{\partial x^{\lambda}}{\partial x'^{\mu}} \] so gilt die Matrixgleichung \[ \Theta' = J^{-1} \, \Theta \, J + J^{-1} \, dJ \] Dabei ist \(\Theta'\) die Matrix bezüglich der neuen Koordinaten \(x'\), und \(dJ\) ist die Matrix mit Elementen analog zur Definition von \(d\phi\) im Kapitel über Co-Tangentialvektoren. Details ersparen wir uns hier.
Einige weitere Anmerkungen:
Wenn wir eine Einbettung voraussetzen, lässt sich die Richtungsableitung eines Vektorfeldes \(u\) in \(\gamma'(0)\)-Richtung in \(t = 0\) durch den üblichen Grenzwert des Differenzenquotienten ausdrücken: \[ \frac{d}{dt} u(\gamma(t)) \bigg|_{t = 0} = \lim_{ t \rightarrow 0} \, \frac{1}{t} \, [u(\gamma(t)) - u(\gamma(0))] \] Man kann aufgrund des Einbettungsraumes direkt die Differenz der zwei Vektoren an verschiedenen Orten bilden.
Ohne Einbettung geht das nicht, denn \(u(\gamma(t))\) und \(u(\gamma(0))\) gehören zu zwei verschiedenen Tangentialräumen. Deshalb ist die obige Richtungsableitung ohne Einbettung gar nicht definiert, und wir haben sie durch die kovariante Ableitung ersetzt, die die obige Richtungsableitung auf den Tangentialraum in \(p = \gamma(0)\) projeziert. Die kovariante Ableitung benötigt keine Einbettung.
Man kann sich nun die Frage stellen, ob sich für die kovariante Ableitung ein Ausdruck analog zu oben finden lässt, bei dem eine Art Unterschied zwischen Tangentialvektoren an verschiedenen Stellen der Mannigfaltigkeit eine Rolle spielt.
Das Problem ist, dass die Differenz oben die Tangentialvektoren an zwei unterschiedlichen Punkten \(\gamma(t)\) und \(\gamma(0) = p\) miteinander vergleicht. Wir dürfen ohne Einbettung jedoch nur Tangentialvektoren des gleichen Tangentialraums voneinander abziehen, denn nur dort ist die Vektordifferenz überhaupt definiert (der Tangentialraum ist ja ein Vektorraum).
Der Tangentialvektor \(u(\gamma(t))\) muss dazu irgendwie vom Punkt \(\gamma(t)\) zum Punkt \(\gamma(0) = p\) verschoben (transportiert) werden, und zwar so, dass anschließend der obige Ausdruck gerade die kovariante Ableitung ergibt. Nennen wir den Transportoperator, der aus \(u(\gamma(t))\) einen Tangentialvektor in \( \gamma(0) = p \) macht \(T(\gamma)_{-t}\), d.h. \[ T(\gamma)_{-t} \, u(\gamma(t)) \] ist ein Tangentialvektor in \(p\). Wir können \( T(\gamma)_{-t} \) so lesen, dass dieser Operator einen sogenannten Paralleltransport entlang der Kurve \(\gamma\) bewirkt, und zwar so, dass der Kurvenparameter um \( - t \) geändert wird. Allgemein soll der Paralleltransportoperator \( T(\gamma)_{t} \) aus einem Tangentialvektor im Tangentialraum \(T(\gamma(s))\) einen Tangentialvektor im Tangentialraum \(T(\gamma(s + t))\) machen. Also ist \( T(\gamma)_{t} \) eine Abbildung vom Tangentialraum \(T(\gamma(s))\) in den Tangentialraum \(T(\gamma(s + t))\) für jeden Startwert \(s\) des Kurvenparameters: \[ T(\gamma)_{t} : \, T(\gamma(s)) \rightarrow T(\gamma(s + t)) \] Dabei soll \( T(\gamma)_{0} = 1 \) sein, denn der Transport um Nichts soll auch Nichts ändern.
Wir wollen den Transportoperator nun so konstruieren, dass folgendes für die kovariante Ableitung in \(v(p)\)-Richtung (also entlang der Kurve \(\gamma\) bei \(p = \gamma(0)\) ) gilt: \[ D_{v(p)} u = \lim_{ t \rightarrow 0} \, \frac{1}{t} \, [ T(\gamma)_{-t} \, u(\gamma(t)) - u(\gamma(0)) ] \] wobei \(v(p)\) der zur Kurve \(\gamma(t)\) gehörende Tangentialvektor in \(t = 0\) ist.
Insgesamt wollen wir einen möglichst einfachen Transportoperator konstruieren. Da der Transportoperator eine Abbildung zwischen zwei Vektorräumen ist, wollen wir versuchen, mit einem linearen Transportoperator auszukommen. Außerdem soll \[ T(\gamma)_{t'} \, T(\gamma)_{t} = T(\gamma)_{t + t'} \] gelten, was der Vorstellung entspricht, dass der Transportoperator einen Tangentialvektor entlang einer Kurve verschiebt, wobei man den Transport um \(t + t'\) in zwei Teiltransporte zerlegen kann (wie üblich, muss man diese Operator-Beziehung von rechts nach links lesen: erst wird immer der Operator rechts ausgeführt). Setzt man hier \( t' = - t \), so folgt \[ T(\gamma)_{-t} \, T(\gamma)_{t} = 1 \] d.h. ein Transport hin und wieder zurück ändert nichts. Wichtig ist bei all diesen Regeln, dass immer dieselbe Kurve \(\gamma\) für den Transport verwendet wird. Das Transportergebnis kann ja vom Transportweg abhängen (und tut es auch im Allgemeinen)!
Für die folgende Rechnung ist es günstig, den Tangentialvektor \(u(\gamma(t))\) nach den Basisvektoren \[ T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] zu entwickeln. Dies sind die von \(p = \gamma(0)\) nach \(\gamma(t)\) paralleltransportierten Basisvektoren \( \frac{\partial}{\partial x^{\mu}} \big|_{p} \). Wir schreiben also \[ u(\gamma(t)) =: \sum_{\mu} \, w^{\mu}(\gamma(t)) \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] mit entsprechenden Entwicklungskoeffizienten \(w^{\mu}(\gamma(t))\). Vorsicht: die nach \(\gamma(t)\) paralleltransportierten Basisvektoren \( T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \big|_{p} \) müssen nicht identisch sein mit den dortigen Koordinaten-Basisvektoren \( \frac{\partial}{\partial x^{\mu}} \big|_{\gamma(t)} \). Deswegen haben wir die Vektor-Koeffizienten hier auch \( w^{\mu}(\gamma(t)) \) anstatt \( u^{\mu}(\gamma(t)) \) genannt.
Wir wollen nun die kovariante Ableitung im Punkt \(\gamma(t)\) (also nicht in \(p = \gamma(0)\) ) ausrechnen: \[ D_{v(\gamma(t))} u = \lim_{ \epsilon \rightarrow 0} \, \frac{1}{\epsilon} \, [ T(\gamma)_{- \epsilon} \, u(\gamma(t + \epsilon)) ] - u(\gamma(t)) ] \] Dabei ist \( v(\gamma(t)) \) der zur Kurve \( \gamma \) gehörende Tangentialvektor im Punkt \( \gamma(t) \). Wenn wir die obige Basisentwicklung von \(u(\gamma(t))\) einsetzen, so erhalten wir aufgrund der geforderten Eigenschaften des Transportoperators (wobei wir voraussetzen, dass die Parallelverschiebung \( T(\gamma)_{- \epsilon} \) die skalaren Koeffizienten \(w^\mu\) nicht verändert; die Begründung folgt gegen Ende des Kapitels): \[ D_{v(\gamma(t))} u = \] \[ = \lim_{ \epsilon \rightarrow 0} \, \frac{1}{\epsilon} \, \left[ T(\gamma)_{- \epsilon} \, u(\gamma(t + \epsilon)) ] - u(\gamma(t)) \right] = \] \[ = \lim_{ \epsilon \rightarrow 0} \, \frac{1}{\epsilon} \, \bigg[ T(\gamma)_{- \epsilon} \, \sum_{\mu} \, w^{\mu}(\gamma(t + \epsilon)) \, T(\gamma)_{t + \epsilon} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} + \] \[ - u(\gamma(t)) \bigg] = \] \[ = \lim_{ \epsilon \rightarrow 0} \, \frac{1}{\epsilon} \, \bigg[ \sum_{\mu} \, w^{\mu}(\gamma(t + \epsilon)) \, T(\gamma)_{- \epsilon} \, T(\gamma)_{t + \epsilon} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} + \] \[ - u(\gamma(t)) \bigg] = \] \[ = \lim_{ \epsilon \rightarrow 0} \, \frac{1}{\epsilon} \, \bigg[ \sum_{\mu} \, w^{\mu}(\gamma(t + \epsilon)) \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} + \] \[ - u(\gamma(t)) \bigg] = \] \[ = \lim_{ \epsilon \rightarrow 0} \, \frac{1}{\epsilon} \, \bigg[ \sum_{\mu} \, w^{\mu}(\gamma(t + \epsilon)) \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} + \] \[ - \sum_{\mu} \, w^{\mu}(\gamma(t)) \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \bigg] = \] \[ = \lim_{ \epsilon \rightarrow 0} \, \frac{1}{\epsilon} \, \sum_{\mu} \, \big[ w^{\mu}(\gamma(t + \epsilon)) + \] \[ - w^{\mu}(\gamma(t)) \big] \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = \] \[ = \sum_{\mu} \, \frac{d}{dt'} w^{\mu}(\gamma(t')) \bigg|_{t' = t} \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = \] \[ = \sum_{\mu} \, [v(\gamma(t)) \, w^{\mu}] \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] Andererseits ist die kovariante Ableitung additiv und es gilt die Produktregel, d.h. wir können \(D_{v(\gamma(t))} u \) auch mit Hilfe dieser Regeln berechnen und dann die Ergebnisse mit der obigen Formel vergleichen. Dazu brauchen wir die Basisentwicklung des Tangential-Vektorfeld \(u\): \[ u(\gamma(t)) = \] \[ =\sum_{\mu} \, w^{\mu}(\gamma(t)) \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = \] \[ =: \left[ \sum_{\mu} \, w^{\mu} \, T(\gamma) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \right] (\gamma(t)) \] mit \[ \left[ T(\gamma) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \right] (\gamma(t)) := T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] Der Operator \(T(\gamma)\) erzeugt dabei allgemein aus einem Vektor im Punkt \(p\) durch Paralleltransport ein komplettes Vektorfeld entlang der Kurve \(\gamma\), das die obige Formel (linke Seite) im Kurvenpunkt \(\gamma(t)\) auswertet. Aufgrund der Eigenschaften der kovarianten Ableitung gilt nun: \[ D_{v(\gamma(t))} u = \] \[ = D_{v(\gamma(t))} \, \sum_{\mu} \, w^{\mu} \, T(\gamma) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = \] \[ = \sum_{\mu} \, [v(\gamma(t)) \, w^{\mu}] \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} + \] \[ + \sum_{\mu} \, w^{\mu}(\gamma(t)) \, D_{v(\gamma(t))} \, T(\gamma) \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] Vergleichen wir dies mit dem Ergebnis für \( D_{v(\gamma(t))} u \) von etwas weiter oben, also mit \[ D_{v(\gamma(t))} u = \] \[ = \sum_{\mu} \, [v(\gamma(t)) \, w^{\mu}] \, T(\gamma)_{t} \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] so sehen wir, dass diese Formel genau den ersten Term unserer neuen Formel reproduziert, aber nicht den zweiten. Der zweite Term muss also Null sein, d.h. es muss gelten: \[ D_{v(\gamma(t))} \, T(\gamma) \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = 0 \] Die kovariante Ableitung der Basisvektoren in \(\gamma\)-Richtung, die durch Parallelverschiebung entlang dieser Kurve \(\gamma\) aus den Basis-Tangentialvektoren \( \frac{\partial}{\partial x^{\mu}} \big|_{p} \) bei \(\gamma(0) = p\) entstehen, muss Null sein. Das gilt für jeden Punkt \(\gamma(t)\) der Kurve.
Wir können nun mit Hilfe von \(T(\gamma)\) aus einem festen Vektor \(u(p)\)
allgemein ein Vektorfeld entlang der Kurve \(\gamma\) definieren durch
\[
T(\gamma)_{t} \, u(p)
=: [T(\gamma) u(p)] (\gamma(t))
\]
Das Vektorfeld \( T(\gamma) u(p) \)
wollen wir als Parallel-Vektorfeld längs der Kurve \(\gamma\) bezeichnen.
Jeder Vektor dieses Vektorfeldes geht dabei durch eine Parallelverschiebung aus dem
festen Vektor \(u(p)\) hervor, d.h. \(T(\gamma)\) erzeugt aus einem festen Vektor \(u(p)\)
durch Parallelverschiebung entlang von \(\gamma\)
das entlang \(\gamma\) parallele Vektorfeld \( [T(\gamma) u(p)] \).
Dabei ist speziell
\[
[T(\gamma) u(p)](p) = u(p)
\]
An dieser Stelle noch eine kurze Nebenbemerkung:
Man kann in Analogie zum Push-Forward-Fluss der Lie-Ableitung (siehe ein späteres Kapitel)
auch noch das parallelverschobene Vektorfeld \( T(\gamma)_{t} \, u \)
auf der Kurve \(\gamma\) definieren. Dieses Vektorfeld geht aus dem Vektorfeld \(u\)
dadurch hervor, dass jeder Vektor \(u(\gamma(t'))\) um ein festes \(t\) parallelverschoben wird:
\[
T(\gamma)_{t} u(\gamma(t'))
=: [T(\gamma)_{t} \, u](\gamma(t' + t))
\]
Entsprechend könnten wir in der Formel für die kovariante Ableitung
\[
T(\gamma)_{-t} \, u(\gamma(t)) =
[T(\gamma)_{-t} u] (p)
\]
mit \(p = \gamma(0)\) einsetzen.
Die Formel für die kovariante Ableitung sieht dann vollkommen analog
zur Formel der Lie-Ableitung aus, die wir in einem späteren Kapitel noch
kennenlernen werden.
Wie sieht es mit der kovarianten Ableitung \( D_{v(\gamma(t))} [T(\gamma) u(p)] \) des Parallelfeldes aus? Um unser obiges Ergebnis bezüglich der Basisvektoren verwenden zu können, zerlegen wir \( T(\gamma) u(p) \) nach dieser Basis: \[ [T(\gamma) u(p)] (\gamma(t)) = \] \[ = T(\gamma)_{t} \, u(p) = \] \[ = T(\gamma)_{t} \, \sum_{\mu} \, u^{\mu}(p) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = \] \[ = \sum_{\mu} \, u^{\mu}(p) \, T(\gamma)_{t} \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = \] \[ = \sum_{\mu} \, u^{\mu}(p) \, \left[ T(\gamma) \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \right] (\gamma(t)) \] also \[ T(\gamma) u(p) = \sum_{\mu} \, u^{\mu}(p) \, \left[ T(\gamma) \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \right] \] Dabei sind die Komponenten \(u^{\mu}(p)\) feste Zahlenwerte, die nicht von \(\gamma(t)\) abhängen. Die Parallelverschiebung verändert also die Komponenten \(u^{\mu}(p)\) des Startvektors \(u(p)\) nicht, sondern wirkt sich nur auf die Basisvektoren aus, die von \(p\) an die anderen Punkte der Verschiebungskurve paralleltransportiert werden.
Für die kovariante Ableitung haben wir dann: \[ D_{v(\gamma(t))} [T(\gamma) u(p)] = \] \[ = D_{v(\gamma(t))} \, \sum_{\mu} \, u^{\mu}(p) \, T(\gamma) \frac{\partial}{\partial x^{\mu}} \bigg|_{p} = \] \[ = \sum_{\mu} \, u^{\mu}(p) \, D_{v(\gamma(t))} \left[ T(\gamma) \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \right] = \] \[ = 0 \] Unser Ergebnis lautet also:
Der lineare Parallel-Transportoperator mit den oben geforderten Eigenschaften muss die
Gleichung
\[
D_{v(\gamma(t))} [T(\gamma) u(p)] = 0
\]
in jedem Punkt \(\gamma(t)\) dieser Verschiebungskurve erfüllen. Ander ausgedrückt:
Anschaulich bedeutet das (bei einer Einbettung):
|

Wir können unsere Startgleichung
\[
D_{v(\gamma(t))} u =
\lim_{ \epsilon \rightarrow 0} \,
\frac{1}{\epsilon} \, [ T(\gamma)_{- \epsilon} \, u(\gamma(t + \epsilon)) ] - u(\gamma(t)) ]
\]
übrigens noch etwas anders schreiben, indem wir darin \(t = 0\) einsetzen
und \( \gamma(t) = \gamma(0) = p \) verwenden sowie statt \(\epsilon\) jetzt \(t\) schreiben:
\[
D_{v(p)} u =
\lim_{t \rightarrow 0} \,
\frac{1}{t} \, [ T(\gamma)_{-t} \, u(\gamma(t)) ] - u(p) ]
\]
Dieser Zusammenhang zwischen Paralleltransport und kovarianter Ableitung
wird uns in ganz analoger Form bei der Lie-Ableitung in einem späteren Kapitel
wiederbegegnen. Man benötigt dabei eine Abbildung zwischen verschiedenen Tangentialräumen
entlang einer Kurve. Bei der kovarianten Ableitung ist dies der Paralleltransport;
bei der Lie-Ableitung dagegen verwenden wir eine sogenannte Fluss-Abbildung.
Diese Abbildung definiert gleichsam das Referenz-Vektorfeld, mit dem man das
gegebene Vektorfeld vergleicht und so eine Ableitung des Vektorfeldes
definieren kann. Bei der kovarianten Ableitung ist das Referenz-Vektorfeld
durch das längs einer Kurve \(\gamma\) parallele Vektorfeld gegeben.
Entsprechend ist die kovariante Ableitung dieses Referenz-Vektorfeldes
in Kurvenrichtung Null, denn man misst ja durch die kovariante Ableitung
gerade die Änderung gegenüber dem Referenz-Vektorfeld.
Noch eine Bemerkung zur Vorgehensweise: Im vorliegenden Kapitel sind wir von einer Definition der kovarianten Ableitung ausgegangen und haben daraus den Paralleltransport und damit das Referenzvektorfeld herleiten können. In der Literatur (z.B. in Matt Visser: Math 464: Notes on differential geometry, Victoria University of Wellington) wird teilweise auch anders herum vorgegangen und zunächst der Paralleltransport konstruiert, bevor man daraus die zugehörige kovariante Ableitung herleitet. Diese Vorgehensweise bietet sich später bei der Lie-Ableitung an, bei der wir von der Fluss-Abbildung ausgehen werden und daraus die Lie-Ableitung herleiten werden.
Wir können nun die Bedingung \[ D_{v(\gamma(t))} [T(\gamma) u(p)] = 0 \] dazu verwenden, die Wirkung des Parallel-Transportoperators durch eine Differenzialgleichung zu beschreiben. Dazu müssen wir die Bedingung einfach nur in Koordinaten ausschreiben. Um die Schreibweise zu vereinfachen, verlangen wir von unserem Vektorfeld \(u\), dass es von Anfang an ein Parallelfeld längs \(\gamma\) ist, d.h. es soll gelten: \[ u(\gamma(t)) = T(\gamma)_{t} \, u(p) \] oder kurz \[ u = T(\gamma) u(p) \] Das Vektorfeld entlang der Kurve soll also durch Parallelverschiebung entstehen. Legen wir los: \[ D_{v(\gamma(t))} [T(\gamma) u(p)] = D_{v(\gamma(t))} u = \] \[ = \sum_{\rho} \, \bigg( \frac{d}{dt'} u^{\rho}(\gamma(t')) \bigg|_{t' = t} + \] \[ + \sum_{\mu\nu} \, u^{\mu}(\gamma(t)) \, \Gamma^{\rho}_{\nu\mu}(\gamma(t)) \, v^{\nu}(\gamma(t)) \bigg) \, \frac{\partial}{\partial x^{\rho}} \bigg|_{\gamma(t)} = \] \[ = 0 \] Das bedeutet:
|
Differenzialgleichung für ein Parallelfeld längs einer Kurve: Das Tangentialvektorfeld \[ u(\gamma(t)) = \sum_{\mu} \, u^{\mu}(\gamma(t)) \, \frac{\partial}{\partial x^{\mu}}\bigg|_{\gamma(t)} \] ist ein Parallelfeld längs der vorgegebenen Kurve \(\gamma\), wenn seine Koeffizienten \( u^{\mu}(\gamma(t)) \) in jedem Punkt der Kurve die Differenzialgleichung \[ \frac{d}{dt'} u^{\rho}(\gamma(t')) \bigg|_{t' = t} + \] \[ + \sum_{\mu\nu} \, u^{\mu}(\gamma(t)) \, \Gamma^{\rho}_{\nu\mu}(\gamma(t)) \, v^{\nu}(\gamma(t)) = \] \[ = 0 \] erfüllen. Dabei sind \(v^{\nu}(\gamma(t))\) die vorgegebenen Koeffizienten des zu \(\gamma(t)\) gehörenden Tangentialvektors. Man kann diese Differenzialgleichung auch als Matrixgleichung in der Kurzform \[ v(\gamma(t)) \, u + \Theta(v) \, u(\gamma(t)) = 0 \] schreiben, wobei \( u(\gamma(t)) \) und \( v(\gamma(t)) \, u \) als Spaltenvektoren zu lesen sind und \( \Theta(v) \) eine Matrix ist – die genaue Definition hatten wir weiter oben bereits gegeben. |
Das Lösen dieser Differenzialgleichung entspricht dem Ausrechnen der Wirkung
des Parallel-Transportoperators.
Sind beispielsweise als Anfangswert die Werte \( u^{\mu}(\gamma(0)) \) vorgegeben (d.h. \(u(p)\) ist vorgegeben), so liefert die Lösung der Differenzialgleichung die Werte \( u^{\mu}(\gamma(t)) \) und damit den nach \(\gamma(t)\) parallelverschobenen Tangentialvektor.
Da es sich um eine lineare Differenzialgleichung erster Ordnung für \( u^{\mu}(\gamma(t)) \) handelt, ist die Lösung bei vorgegebenem Anfangswert eindeutig bestimmt. Man kann daher die Differenzialgleichung als eindeutige Definition des Parallel-Transportoperators auffassen. Diese Definition ist konsistent zu den oben geforderten Eigenschaften des Parallel-Transportoperators, denn die Lösung \( u^{\mu}(\gamma(t)) \) der Differenzialgleichung hängt linear von den Anfangsbedingungen \( u^{\mu}(\gamma(0)) \) ab, und auch die anderen Eigenschaften kann man nachweisen.
Damit ist es uns tatsächlich gelungen, den gewünschten Parallel-Transportoperator eindeutig zu konstruieren. Ist ein affiner Zusammenhang (eine kovariante Ableitung) gegeben, so ist der Paralleltransport eindeutig festgelegt und umgekehrt, wie unsere obigen Überlegungen zeigen.
Das Einzige, was uns noch fehlt, ist eine explizite Formel für den Parallel-Transportoperator. In der Mathematik verzichtet man zumeist auf eine solche Formel, da die Differenzialgleichung oben bereits alle Informationen enthält. In der Physik dagegen kennt man aus ähnlichen Fragestellungen bereits explizite Formeln für solche Lösungs-Operatoren von linearen Differenzialgleichungen. Ein bekanntes Beispiel ist die Lösung der zeitabhängigen Schrödingergleichung in der Quantenmechanik. Man braucht nur noch den Formalismus auf unser obiges Problem zu übertragen.
Die Details der Konstruktion wollen wir hier überspringen. Man findet die Ideen in jedem Buch über Quantenmechanik (Stichworte: zeitabhängige Schrödingergleichung, Zeitordnung, Störungstheorie) oder aber in dem unten angegebenen Skript von Matt Visser in Anhang D. Das Ergebnis ist das sogenannte weggeordnete Integral (path ordered integral). Im Rahmen der Eichtheorie wird daraus der Eich-Transportoperator, der bei einem geschlossenen Weg (d.h. Anfangspunkt gleich Endpunkt) zum sogenannten Wilson loop wird. Wir werden hier nicht näher darauf eingehen.
Man kann die Idee des Paralleltransports dazu nutzen, um eine möglichst gerade Kurve zu konstruieren. Eine solche Kurve wollen wir geodätische Linie nennen. Dabei soll möglichst gerade bedeuten, dass die Tangentialvektoren entlang der Kurve bis auf einen Faktor durch Parallelverschiebung auseinander hervorgehen. Anschaulich bedeutet das bei einer Einbettung, dass sich der Tangentialvektor der Kurve nur senkrecht zur Tangentialfläche sowie parallel zu sich selbst ändern darf. Veranschaulichen wir uns den Tangentialvektor als Geschwindigkeit, so darf die Beschleunigung also nur senkrecht zur Fläche wirken (wird benötigt, damit die Geschwindigkeit im Lauf der Bewegung tangential zur Fläche bleibt) sowie in Bewegungsrichtung beschleunigend oder abbremsend wirken. Nach rechts oder links darf man auf der Fläche also nicht abbiegen.
Wichtig ist also, dass innerhalb der Tangentialfläche keine Beschleunigung zur Seite stattfindet. Übertragen auf ein Schiff im Ozean bedeutet das: Das Schiff fährt immer geradeaus, weder nach rechts, noch nach links. Dabei darf es auch mal schneller oder langsamer werden. Aufgrund der Erdkrümmung gibt es während der Fahrt eine kleine Beschleunigung senkrecht zur Wasseroberfläche, denn das Schiff verlässt die Wasseroberfläche nicht.
Man kann durch Umparametrisierung der Kurve erreichen, dass die parallele Beschleunigung gleich Null wird, d.h. die Bewegung erfolgt dann mit konstanter Geschwindigkeit. Das wäre dann eine spezielle Parametrisierung der geodätischen Linie. Für unser Schiff bedeutet das, dass es mit gleichmäßiger Geschwindigkeit über die Wellen gleitet.
Man kann sich eine geodätische Linie auf einer gekrümmten Fläche auch noch anders veranschaulichen. Dazu stellen wir uns vor, dass wir ein dünnes langes gerades Band, z.B. aus einem dünnen Blech, flach auf einer gekrümmten Fläche anbringen. Das Band liegt dann entlang einer geodätischen Linie auf der Fläche, da es so beschaffen sein soll, dass es sich nur senkrecht zur Fläche biegen lässt.
Präzisieren wir diese Überlegung: Wir verlangen, dass die kovariante Ableitung des Tangentialvektors \( v(\gamma(t)) \) der Kurve \( \gamma \) an jedem Punkt \(\gamma(t)\) derselben Kurve proportional zum Tangentialvektor selbst ist. Es soll also gelten: \[ D_{v(\gamma(t))} v = c(t) \, v(\gamma(t)) \] wobei man durch Umparametrisierung der Kurve \( c(t) = 0 \) erreichen kann, so dass die Tangentialvektoren der Kurve ein Parallelfeld entlang der Kurve bilden. Natürlich kann man auch diese Gleichung bezüglich einer Koordinatenfunktion \(f\) in Komponenten ausschreiben:
|
Differenzialgleichung einer geodätischen Linie in Koordinatendarstellung: \[ \frac{d}{dt'} dv^{\rho}(\gamma(t')) \bigg|_{t' = t} \, + \] \[ + \sum_{\mu\nu} \, v^{\mu}(\gamma(t)) \, \Gamma^{\rho}_{\nu\mu}(\gamma(t)) \, v^{\nu}(\gamma(t)) = \] \[ = c(t) \, v^{\rho}(\gamma(t)) \] oder in Matrix-Kurzform mit entsprechenden Spaltenvektoren: \[ v(\gamma(t)) \, v + \Theta(v) \, v(\gamma(t)) = c(t) \, v(\gamma(t)) \] |
mit
\[
\frac{d}{dt'} (f \circ \gamma)^{\mu}(t') \bigg|_{t' = t} =
v^{\mu}(\gamma(t))
\]
Es gilt nun, diese Differenzialgleichung \( v^{\rho}(\gamma(t)) \) bei vorgegebenen
Anfangswerten und gegebenen Christoffelsymbolen zu lösen
und dann durch Integration die Kurvenkoordinaten \( (f \circ \gamma)^{\mu}(t) \)
zu bestimmen, wobei man meist \( c(t) = 0 \) setzt und damit die Parametrisierung der Kurve
gleich festlegt. Übrigens: wegen der Symmetrie in \(\mu\) und \(\nu\) spielt Torsion
in dieser Gleichung keine Rolle.
Wir hatten oben bereits erwähnt, dass man die kovariante Ableitung für Co-Tangentialvektoren \( \omega(p) \) über die Produktregel \[ D_{v(p)} (\omega \, u) =: \omega(p) \, (D_{v(p)} \, u) + (D_{v(p)} \omega) \, u(p) \] definieren kann. Da \( \phi := (\omega u) \) eine skalare Funktion ist, ist dabei \[ D_{v(p)} (\omega \, u) = v(p) \, (\omega \, u) \] Der Paralleltransport ermöglicht es uns, diese Vorgehensweise besser zu verstehen. Wir können nämlich nicht nur Tangentialvektoren, sondern auch Co-Tangentialvektoren paralleltransportieren, indem wir fordern, dass bei diesem Paralleltransport der Wert der skalaren Funktion \( (\omega \, u) \) sich nicht ändern soll. Anschaulich sagen wir ja, dass der Paralleltransport einen Tangentialvektor \(v(p)\) so wenig wie möglich ändert (was bei einer Einbettung unmittelbar eine anschauliche Bedeutung hat). Analog wollen wir auch, dass der Paralleltransport einen Co-Tangentialvektor \(\omega(p)\) so wenig wie möglich ändert. Dazu passt dann, dass sich \( (\omega(p) \, u(p)) \) beim gleichzeitigen Paralleltransport von \(\omega(p)\) und \(u(p)\) überhaupt nicht ändert.
Wir definieren also den Paralleltransport der skalaren Funktion \[ \phi(p) := (\omega \, u)(p) := \omega(p) \, u(p) \] durch \[ [T(\gamma) \, \phi(p)](\gamma(t)) := T(\gamma)_{t} \, \phi(p) := \phi(p) \] und somit dann \[ [T(\gamma) \, (\omega \, u)(p)](\gamma(t)) := \] \[ := T(\gamma)_{t} \, (\omega \, u)(p) := \] \[ := (\omega \, u)(p) = \omega(p) \, u(p) \] d.h. die Funktion \( [T(\gamma) \, (\omega \, u)(p)] \) ist entlang der Kurve \(\gamma\) konstant. Diese Definition des Paralleltransports einer skalaren Funktion ist zwingend, wenn wir für die kovariante Ableitung einer skalaren Funktion \(\phi\) die Formel \[ D_{v(p)} \phi = \lim_{ t \rightarrow 0} \, \frac{1}{t} \, [ T(\gamma)_{-t} \, \phi(\gamma(t)) - \phi(\gamma(0)) ] \] analog zur Formel für Tangentialvektoren erreichen wollen. Aus der Konstanz von \(\phi\) beim Paralleltransport folgt nämlich \[ T(\gamma)_{-t} \, \phi(\gamma(t)) = \phi(\gamma(t)) \] (so etwas hatten wir weiter oben bereits für die skalaren Koeffizienten \(w^\mu\) vorausgesetzt) so dass \[ D_{v(p)} \phi = \] \[ = \lim_{ t \rightarrow 0} \, \frac{1}{t} \, [ T(\gamma)_{-t} \, \phi(\gamma(t)) - \phi(\gamma(0)) ] =\] \[ = \lim_{ t \rightarrow 0} \, \frac{1}{t} \, [ \phi(\gamma(t)) - \phi(\gamma(0)) ] = \] \[ = \frac{d}{dt} \phi(\gamma(t)) \bigg|_{t = 0} = v(p) \, \phi \] ist. Genau so war ja die kovariante Ableitung einer skalaren Funktion definiert. Das macht auch deshalb Sinn, weil wir ja für den Vergleich der skalaren Funktionswerte an den beiden Stellen \(\gamma(t)\) und \(\gamma(0)\) gar keinen Paralleltransport \( T(\gamma)_{-t} \) brauchen, anders als bei den Tangentialvektoren. Bei skalaren Funktionen soll der Paralleltransport also gar nichts verändern.
Damit können wir nun den Paralleltransport des Co-Tangentialvektors \(\omega(p)\) definieren durch \[ \omega(p) \, u(p) = T(\gamma)_{t} \, (\omega \, u)(p) =: \] \[ =: [T(\gamma)_{t} \, \omega(p)] \, [T(\gamma)_{t} \, u(p)] \] d.h. der gleichzeitige Paralleltransport von \(\omega(p)\) und \(u(p)\) entlang der Kurve ändert den Wert der Kombination dieser beiden Vektoren nicht.
Die kovariante Ableitung eines Co-Tangentialvektors \(\omega\) definieren wir nun analog zu skalaren Funktionen und Tangentialvektoren durch \[ D_{v(p)} \omega = \] \[ = \lim_{ t \rightarrow 0} \, \frac{1}{t} \, [ T(\gamma)_{-t} \, \omega(\gamma(t)) - \omega(\gamma(0)) ] = \] \[ = \frac{d}{dt} \, T(\gamma)_{-t} \, \omega(\gamma(t)) \bigg |_{t = 0} \] Nun ist \( T(\gamma)_{-t} \, \omega(\gamma(t)) \) ein Co-Tangentialvektor im Punkt \(\gamma(0) = p\), den wir schreiben können als \[ T(\gamma)_{-t} \, \omega(\gamma(t)) = \] \[ = \sum_{\mu} \, [ T(\gamma)_{-t} \, \omega(\gamma(t)) ]_{\mu}(p) \, dx^{\mu}|_{p} \] d.h. die \(t\)-Abhängigkeit steckt alleine in den Koeffizienten.
Analog ist es beim Tangentialvektor \[ T(\gamma)_{-t} \, u(\gamma(t)) = \] \[ = \sum_{\mu} \, [ T(\gamma)_{-t} \, u(\gamma(t)) ]^{\mu}(p) \, \frac{\partial}{\partial x^{\mu}} \bigg|_{p} \] Daraus folgt, dass wir in der folgenden Rechnung die Produktregel anwenden dürfen: \[ v(p) \, (\omega \, u) = D_{v(p)} \, (\omega \, u) = \] \[ = \frac{d}{dt} (\omega \, u)(\gamma(t)) \bigg|_{t = 0} = \] ... wir verwenden die Konstanz von \( (\omega \, u) \) beim Paralleltransport: \[ = \frac{d}{dt} [ T(\gamma)_{-t} \, (\omega \, u)(\gamma(t))] \bigg|_{t = 0} = \] ... wir setzen die Definition des Paralleltransports für einen Co-Tangentialvektor ein:
\[ = \frac{d}{dt} [T(\gamma)_{-t} \, \omega(\gamma(t))] \, [T(\gamma)_{-t} \, u(\gamma(t))] \bigg|_{t = 0} = \] ... umschreiben in Komponenten ergibt: \[ = \frac{d}{dt} \, \sum_{\mu} \, [T(\gamma)_{-t} \, \omega(\gamma(t))]_{\mu} \, [T(\gamma)_{-t} \, u(\gamma(t))]^{\mu} \bigg|_{t = 0} = \] ... Produktregel anwenden: \[ = \sum_{\mu} \, \frac{d}{dt} [T(\gamma)_{-t} \, \omega(\gamma(t))]_{\mu} \bigg|_{t = 0} \, u^{\mu}(p) + \] \[ + \sum_{\mu} \, \omega_{\mu}(p) \, \frac{d}{dt} [T(\gamma)_{-t} u(\gamma(t))]^{\mu} \bigg|_{t = 0} = \] ... die Definition der kovarianten Ableitung für Tangential- und Co-Tangentialvektoren über den Paralleltransport ergibt: \[ = \sum_{\mu} \, [D_{v(p)} \omega]_{\mu} \, u^{\mu}(p) + \sum_{\mu} \, \omega_{\mu}(p) \, [D_{v(p)} u]^{\mu} = \] \[ = [D_{v(p)} \omega] \, u(p) + \omega(p) \, [D_{v(p)} u] \] Damit haben wir die Produktregel von oben reproduziert. Fassen wir zusammen:
|
Erweiterung von Paralleltransport und kovarianter Ableitung
auf Co-Tangentialvektoren und skalare Funktionen:
Gegeben ist entweder die Definition von kovarianter Ableitung oder
Paralleltransport von Tangentialvektoren (in diesem Kapitel haben
wir die kovariante Ableitung als Grundlage definiert).
Das jeweils andere Objekt (kovarianter Ableitung oder
Paralleltransport) ist definiert über
\[
D_{v(p)} u
=
\]
\[ =
\lim_{ t \rightarrow 0} \,
\frac{1}{t} \, [ T(\gamma)_{-t} \, u(\gamma(t)) - u(\gamma(0)) ]
=
\]
\[ =
\frac{d}{dt} \, T(\gamma)_{-t} \, u(\gamma(t)) \bigg|_{t = 0}
\]
Genau denselben Zusammenhang zwischen Paralleltransport und kovarianter
Ableitung möchten wir auch für skalare Funktionen \(\phi\)
und für Co-Tangentialvektoren \(\omega\) erreichen:
\[
D_{v(p)} \phi
=
\]
\[ =
\lim_{ t \rightarrow 0} \,
\frac{1}{t} \, [ T(\gamma)_{-t} \phi(\gamma(t)) - \phi(\gamma(0)) ]
=
\]
\[
\frac{d}{dt} \, T(\gamma)_{-t} \, \phi(\gamma(t)) \bigg|_{t = 0}
\]
|
Die Formeln
\[
\omega(p) \, u(p) =
\]
\[ =
T(\gamma)_{t} \, (\omega u )(p) =:
\]
\[
=: [T(\gamma)_{t} \, \omega(p)] \, [T(\gamma)_{t} \, u(p)]
\]
sowie
\[
v(p) \, (\omega \, u) =
\]
\[ =
D_{v(p)} \, (\omega \, u)
=
\]
\[ =
[D_{v(p)} \omega] \,
u(p)
+
\omega(p) \,
[D_{v(p)} \, u]
\]
sind im Grunde gleichwertig. Man kann entweder über die erste Formel den Paralleltransport
von \(\omega\) definieren (dann legt die zweite Formel die dazu passende kovariante Ableitung fest),
oder man definiert über die zweite Formel die kovariante Ableitung
(dann legt die erste Formel den dazu passenden Paralleltransport fest).
In der Literatur findet man beide Vorgehensweisen.
Die obige Vorgehensweise ist nicht auf Co-Tangentialvektoren beschränkt. Man kann mit ihr schrittweise die kovariante Ableitung beliebigen Tensoren definieren. Betrachten wir als Beispiel die bilineare Abbildung \[ g(p)(u(p), w(p)) \] die zwei Tangentialvektoren aus \(T(p)\) eine reelle Zahl zuordnet (die Metrik ist ein Beispiel für eine solche Abbildung). In Komponenten ausgeschrieben haben wir \[ g(p)(u(p), w(p)) = \] \[ = \sum_{\mu\nu} \, g_{\mu\nu}(p) \, u^{\mu}(p) \, w^{\nu}(p) \] d.h. die \(p\)-Abhängigkeit von \(g(p)(...)\) ist (neben der \(p\)-Abhängigkeit der Argumente \(u(p)\) und \(w(p)\) ) durch die \(p\)-Abhängigkeit der Komponenten \( g_{\mu\nu}(p) \) gegeben.
Wir können nun als skalare Funktion \( g(p)(u(p), w(p)) \) verwenden (analog zu \( \omega(p) \, u(p) \) von oben) und analog zu oben vorgehen:
|
Erweiterung von Paralleltransport und kovarianter Ableitung
auf bilineare skalare Abbildungen (Beispiel: Metrik): \[ g(p)(u(p), w(p)) =: \] \[ =: (T(\gamma)_{t} \,g(p)) \, ( [T(\gamma)_{t} \, u(p)] \, , \, [T(\gamma)_{t} \, w(p)] ) = \] \[ = \sum_{\mu\nu} \, [T(\gamma)_{t} \, g(p)]_{\mu\nu} \, [T(\gamma)_{t} \, u(p)]^{\mu} \, [T(\gamma)_{t} \, w(p)]^{\nu} \] Die zugehörige kovariante Ableitung ist für \(g(p)\) dann definiert durch \[ [D_{v(p)} g]_{\mu\nu} := \] \[ := \lim_{ t \rightarrow 0} \, \frac{1}{t} \, \left\{ [T(\gamma)_{-t} \, g(\gamma(t))]_{\mu\nu} - g_{\mu\nu}(\gamma(0)) \right\} = \] \[ = \frac{d}{dt} \, [T(\gamma)_{-t} \, g(\gamma(t))]_{\mu\nu} \bigg|_{t = 0} \] Wie oben können wir damit für die kovariante Ableitung die folgende Produktregel herleiten: \[ v(p) \, g(u,w) = D_{v(p)} \, g(u,w) = \] \[ = [D_{v(p)} g] \, (u(p), w(p)) + \] \[ + g(p) \, ( D_{v(p)} u \, , \, w(p)) + \] \[ + g(p) \, (u(p) \, , \, D_{v(p)} w) \] |
Interessant ist der Fall
\[
D_{v(\gamma(t))} g = 0
\]
also
\[ [D_{v(\gamma(t))} g]_{\mu\nu}
= 0
\]
für jeden Punkt \(\gamma(t)\) der Kurve.
Die bilineare Abbildung soll sich also in Kurvenrichtung so wenig wie möglich ändern.
Es gilt dann
\[
T(\gamma)_{-t} \, g(\gamma(t)) = g(p)
\]
bzw. umgekehrt
\[
T(\gamma)_{t} \, g(p) = g(\gamma(t))
\]
und somit
\[
v(p) \, g(u,w) =
\]
\[
=
g(p) \, ( D_{v(p)} u \, , \, w(p))
+ \]
\[ +
g(p) \, (u(p) \, , \, D_{v(p)} w)
\]
sowie
\[
g(p)(u(p), w(p)) =
\]
\[ =
g(\gamma(t)) \, ( [T(\gamma)_{t} u(p)] \, , \, [T(\gamma)_{t} w(p)] )
\]
Die erste Gleichung werden in Kapitel 9: Abstände und Winkel: die Metrik
noch kennenlernen:
es handelt sich um die Verträglichkeitsbedingung von Metrik und affinem Zusammenhang.
Wie wir sehen, können wir diese Bedingung auch durch
\( D_{v(\gamma(t))} g = 0 \) abkürzen.
Die zweite Gleichung wiederum besagt, dass sich dann die Metrik
zwischen zwei gleichzeitig paralleltransportierten Tangentialvektoren
nicht ändert.
Soviel zum Thema Kovariante Ableitung und Paralleltransport.
Richtig interessant werden diese Begriffe, wenn wir uns mit den Themen
Krümmung und Metrik befassen und Zusammenhänge zwischen diesen Begriffen
untersuchen. Das wollen wir in den nächsten Kapiteln tun.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 19 September 2023