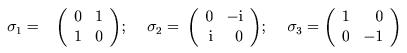
Bei der Drehgruppe und bei der Lorentzgruppe sind wir in den letzten Kapiteln jeweils auf eine einfache Gleichung gestoßen, die den Zusammenhang mit der jeweiligen universellen Überlagerungsgruppe herstellt. Wir erinnern uns (siehe Kapitel 4.6): In der Quantentheorie benötigen wir projektive Darstellungen (Strahldarstellungen) der Symmetriegruppen, um Zustandsvektoren bei einer Drehung oder einem Boost umzurechnen. Projektiv bedeutet, dass bei der Hintereinanderausführung zweier Symmetrietransformationen ein Phasenfaktor in der Darstellung auftreten kann. Bei der Drehgruppe und der Poincaregruppe haben wir gesehen, dass wir sämtliche projektiven Darstellungen erhalten, indem wir alle unitären Darstellungen der universellen Überlagerungsgruppe betrachten. Weitere Phasen können nicht auftreten, da die Lie-Algebra keine zentralen Erweiterungen zulässt.
Der Zusammenhang zwischen der Lorentzgruppe \(SO(1,3)\) (ohne Raum- oder Zeit-Spiegelungen) und ihrer Überlagerungsgruppe \(SL(2,\mathbb{C})\) lautet (siehe Kapitel 4.10):
| Zusammenhang zwischen \(SO(1,3)\) und \(SL(2,\mathbb{C})\): \[ g \, \sigma(x) \, g^+ = \sigma(\Lambda x) \] |
mit \(g \in SL(2,\mathbb{C})\) und \( \Lambda \in SO(1,3)\) sowie \[ \sigma(x) = x^\mu \sigma_\mu \] (mit Summe über \(\mu\) von 0 bis 3) mit den drei Paulimatrizen \( \sigma_i \) (mit \(i\) von 1 bis 3) und der Einheitsmatrix \( \sigma_0 = 1 \). Analog ist es bei der Drehgruppe, denn diese ist eine Untergruppe der Lorentzgruppe: Wir setzen in den obigen Formeln einfach \( x^0 = 0 \) und schreiben \(u \in SU(2)\) und \(R \in SO(3)\) statt \(g\) und \(\Lambda\):
| Zusammenhang zwischen \(SO(3)\) und \(SU(2)\): \[ u \, \sigma(\boldsymbol{x}) \, u^+ = \sigma(R \boldsymbol{x}) \] |
Details dazu siehe Kapitel 4.10. Bleibt die Frage: Wie kommt man auf diesen Zusammenhang? Dieser Frage wollen wir in diesem Kapitel nachgehen.
Das vorliegende Kapitel ist nicht aus einem Guss, denn die Antwort auf diese Frage erarbeite ich mir selbst erst beim Schreiben dieses Kapitels. Ich weiß lediglich, an welchen Landmarken die Reise vorbeiführen wird: Wir werden Begriffen wie Clifford-Algebren, Spingruppen und geometrischer Algebra begegnen und ganz nebenbei die Grundlagen für die Diracgleichung lernen, auf die wir in einem späteren Kapitel noch genauer eingehen. Um den Roten Faden nicht zu verlieren, habe ich mir u.a. spinors-Dirac-checkerboard von Urs Schreiber (Urs.Schreiber@uni-essen.de) als erste Orientierungshilfe herausgesucht (der Link scheint mittlerweile leider nicht mehr zu stimmen und ich konnte es auch nicht wiederfinden). Dort steht:
...
Mathematically, there is a
close relation between spinors and reflections ...
...
The best way to talk about spinors and reflections is, once again,
Clifford algebra ....
Aha! Was aber ist eine Clifford Algebra?
Als Physiker kennt man diesen Begriff von den Dirac-Matrizen \( \gamma_\mu \) – das sind vier 4-mal-4-Matrizen mit komplexwertigen Matrixelementen, die die Eigenschaft
| Diracmatrizen: \[ \gamma_\mu \gamma_\nu + \gamma_\nu \gamma_\mu = 2 g_{\mu\nu} \] |
erfüllen mit der Minkowski-Metrik \(g_{\mu\nu}\) (Diagonalmatrix mit der Diagonale 1, -1, -1, -1 ). Auf der rechten Seite steht genau genommen das Matrixelement \(g_{\mu\nu}\) mal der Einheitsmatrix, die wir aber hier und im Folgenden meist weglassen. Die Dirac-Matrizen werden also durch die Minkowski-Raum-Zeit-Metrik mit bestimmt, wobei es mehrere Möglichkeiten gibt, diese Dirac-Matrizen geeignet zu wählen.
Forscht man etwas weiter, so findet man, dass auch die drei Pauli-Matrizen \( \sigma_i \) (mit \(i\) von 1 bis 3) in dieses Schema passen, denn für sie gilt
| Pauli-Matrizen: \[ \sigma_i \sigma_j + \sigma_j \sigma_i = 2 \delta_{ij} \] |
Die Pauli-Matrizen werden also durch die euklidische Metrik mit bestimmt, wobei es auch hier mehrere Möglichkeiten gibt, die Matrizen geeignet zu wählen. Ganz interessant ist in diesem Zusammenhang die gemeinsame Betrachtung von Dirac- und Paulimatrizen in C.C.Noack: Pauli- und Dirac-Gleichung.
Damit können wir uns nun schrittweise dem Begriff der Clifford-Algebra nähern. Statt mit dem euklidischen Raum oder mit der Raum-Zeit starten wir allgemein mit einem n-dimensionalen reellen Vektorraum \(V\), der eine Metrik \(g\) besitzt (man kann auch komplexe Vektorräume betrachten, was wir hier aber nicht brauchen). Bei geeigneter Basiswahl ist die metrische Matrix \[ g_{\mu\nu} = g(e_\mu , e_\nu ) \] diagonal (es gibt also keine Krümmung) und hat in der Diagonale k Einsen und n-k Minus-Einsen (Achtung: die Metrik \(g\) nicht mit der \(SL(2,\mathbb{C})\)-Matrix \(g\) von oben verwechseln).
Vektoren aus \(V\) bezeichnen wir wie bisher beispielsweise mit \[ x = x^\mu e_\mu \] (mit Summe über \(\mu\)), wobei es \(n\) verschiedene reelle Komponenten \(x^\mu\) gibt. Man sagt nun, der Vektorraum \(V\) zusammen mit der Metrik \(g\) generiert die Clifford-Algebra. Wie tut er das?
Versuchen wir es zunächst mit der Basis-abhängigen Methode: Wir fordern, dass es Objekte \( E_\mu \) in der Clifford-Algebra gibt, so dass analog zu oben
| Universelle Eigenschaft einer Clifford-Algebra (Basis-Darstellung): \[ E_\mu E_\nu + E_\nu E_\mu = 2 g_{\mu\nu} \] |
gilt (Mathematiker verwenden hier teilweise auch andere Faktoren; Physiker schreiben links auch gerne den Antikommutator \( E_\mu E_\nu + E_\nu E_\mu\) \( = \{ E_\mu , E_\nu \} \) hin). Man bezeichnet die \(E_\mu\) auch als Generatoren der Clifford-Algebra.
Offenbar muss eine Multiplikation und eine Addition für diese Generatoren definiert sein. Genau das sagt der Begriff Algebra aus: Eine Algebra ist ein Vektorraum (d.h. man kann addieren und mit Zahlen multiplizieren), bei dem es zusätzlich ein Produkt zwischen den Vektoren gibt, so dass wieder ein Vektor herauskommt. Dieses Produkt erfüllt das Distributivgesetz (Ausmultiplizieren geht) und man kann Zahlen herausziehen (siehe Wikipedia: Algebra over a field ). Bei einer Clifford-Algebra gilt zusätzlich das Assoziativgesetz, d.h. sie ist eine assoziative Algebra.
In Wikipedia: Clifford algebra finden wir, dass Clifford-Algebren eine besondere Form von assoziativen Algebren sind, die man sich als Verallgemeinerung der komplexen Zahlen und der Quaternionen vorstellen kann. Wichtig: das Kommutativgesetz gilt im Allgemeinen nicht. Im Gegenteil – aus der obigen universellen Eigenschaft folgt, dass bei orthonormaler Basis (also diagonaler Metrik) verschiedene Generatoren miteinander antikommutieren, während das Quadrat eines Generators eine Zahl (mal Einheits-Element) ergibt!
Konkret können wir uns die Generatoren \(E_\mu\) als Matrizen vorstellen mit der Matrixmultiplikation zwischen ihnen (beispielsweise Pauli- oder Dirac-Matrizen). Solche Matrizen kann man problemlos addieren und multiplizieren und damit all das tun, was eine assoziative Algebra so hergibt. Wir können aber auch auf diese Konkretisierung verzichten und erst einmal eine abstraktere Begrifflichkeit anstreben, die oft ihre Vorteile hat. Schließlich können wir jederzeit konkret werden und nach passenden Matrizen suchen.
Mit Hilfe der Generatoren können wir nun Linearkombinationen bilden. Dazu können wir einen Vektor \( x = x^\mu e_\mu \) (mit Summe über \(\mu\)) aus \(V\) nehmen und die zugehörige Linearkombination \[ X := x^\mu E_\mu \] in der Clifford-Algebra bilden (natürlich wieder mit Summe über \(\mu\)). Die mit \(x\) gebildete Linearkombination bezeichnen wir dabei mit dem entsprechenden großen Buchstaben \(X\) (analog für andere Vektoren). Diese Formel ist die Verallgemeinerung zu Formeln wie \[ \sigma(x) = x^\mu \sigma_\mu \] oder \[ \gamma(x) = x^\mu \gamma_\mu \] wobei wir jetzt einfach \(X\) für \(\sigma(x)\) oder \(\gamma(x)\) schreiben (das spart viel Schreibarbeit). Richard Feynman hier gerne die Slash-Schreibweise verwendet (siehe auch Wikipedia: Gamma matrices). Übrigens haben wir oben die Schreibweise \( E_\mu \) bereits passend gewählt, denn dazu gehört ja der Basisvektor \(e_\mu\) aus \(V\).
Wir haben damit eine lineare Abbildung vom Vektorraum \(V\) in die Clifford-Algebra, die meist als \(Cl(V,g)\) bezeichnet wird (wir werden auch kurz \(Cl\) schreiben). Diese Abbildung macht aus dem Vektor \(x \in V\) das Clifford-Algebra-Element \(X\) (z.B. eine Matrix). Der Schreibweise in Wikipedia: Clifford algebra folgend nennen wir diese Abbildung \(j\), d.h. \[ j(x) = X \] Man spricht auch von einer injektiven Einbettung des Vektorraums in die Clifford-Algebra, die ihrerseits ja auch ein Vektorraum ist. Beispiele für die Abbildung \(j(x)\) haben wir oben bereits kennengelernt und sie mit \(\sigma(x)\) oder \(\gamma(x)\) bezeichnet. Halten wir fest:
| Einbettung des Vektorraums in die Clifford-Algebra: \[ X := j(x) := x^\mu E_\mu \] |
Natürlich ist dann auch \[ E_\mu = j(e_\mu) \] Damit können wir nun die Gleichung \[ E_\mu E_\nu + E_\nu E_\mu = 2 g_{\mu\nu} \] von oben umschreiben: Wir multiplizieren mit \(x^\mu y^\nu \) und summieren über \(\mu\) und \(\nu\) mit dem Ergebnis:
| Universelle Eigenschaft einer Clifford-Algebra (basisfreie Darstellung): \[ X Y + Y X = 2 \, g(x,y) \] |
Wenn wir basisunabhängig vorgehen wollten, so wäre diese Gleichung eine Forderung an die Abbildung \(j\), die \(x\) zu \(X\) umwandelt und damit \(V\) in \(Cl(V,g)\) einbettet. Wir haben diese Forderung dagegen direkt an die Generatoren \(E_\mu\) gestellt, die diese Abbildung dann festlegen.
Die Gleichung \( X Y + Y X = 2 \, g(x,y) \) hat eine sehr natürliche Struktur, wenn wir die Metrik-Produktstruktur des Vektorraums auf das Algebra-Produkt übertragen wollen. Da das Algebra-Produkt nicht kommutativ sein muss (\(X\) und \(Y\) müssen nicht vertauschbar sein), symmetrisieren wir es und setzen es dann gleich der Metrik, die sowieso symmetrisch in \(x\) und \(y\) ist. Der symmetrische Teil des Algebra-Produktes wird damit in Zukunft den Charakter der Metrik wiedergeben. Mehr dazu weiter unten beim Thema Geometrische Algebra.
Bei einer Clifford-Algebra ist auch ein mehrfaches Produkt von Elementen \(X, Y, Z, \, ... \) möglich. Über die Darstellung \( X = x^\mu E_\mu \) usw. entstehen so mehrfache Produkte der Generatoren \(E_\mu\). Damit stellt sich die Frage: kann man diese Produkte der Generatoren wieder als Linearkombinationen der Generatoren schreiben, oder bilden die Produkte gleichsam neue Basiselemente, bei denen das nicht geht?
Diese Frage kann man mit Hilfe der Gleichung \[ E_\mu E_\nu + E_\nu E_\mu = 2 g_{\mu\nu} \] klären, wobei wir (wie immer) davon ausgehen, dass die Basis in \(V\) orthogonal gewählt wurde, so dass \(g_{\mu\nu}\) diagonal ist. Für \(\mu \ne \nu\) ist damit \[ E_\mu E_\nu + E_\nu E_\mu = 0 \] d.h. \[ E_\mu E_\nu = - E_\nu E_\mu \] für \(\mu \ne \nu\).
Beim Vertauschen zweier ungleicher Generatoren wechselt also das Vorzeichen. So etwas kennt man von einer sogenannten äußeren Algebra her (Dachprodukt), beispielsweise von Differentialformen. Im Unterschied zu einer äußeren Algebra ist aber bei einer Clifford-Algebra das Produkt zweier gleicher Generatoren nicht Null. Insofern ist eine Clifford-Algebra zwar eng mit einer äußeren Algebra verwandt, geht aber zugleich auch darüber hinaus, indem sie die Metrik des Vektorraums in das Algebra-Produkt einbaut. Details dazu wieder weiter (Geometrische Algebra).
Ein Produkt \( E_\mu E_\nu \) ist also als Basiselement gleichwertig zum Produkt \( E_\nu E_\mu \), denn es unterscheidet sich nur durch ein Vorzeichen von diesem. Vertauschungen der Indices ergeben keine neuen Basiselemente. Wenn nun ein längeres Produkt zwei identische Generatoren \(E_\mu\) enthält, so kann man diese durch Vertauschen nebeneinander bringen und dann durch die Zahl \(g_{\mu\mu}\) ersetzen. Produkte mit identischen Generatoren \(E_\mu\) lassen sich also durch kleinere Produkte ersetzen. Damit ist klar, dass wir auch das Eins-Element (z.B. die Einheitsmatrix) als Basiselement mit hinzunehmen sollten, so dass sich beliebige Produkte nach einer Basis entwickeln lassen. Die Basis der Clifford-Algebra zum dreidimensionalen Raum \( \mathbb{R}^3 \) wäre dann gegeben durch \[ 1\] \[ E_1, E_2, E_3 \] \[ E_1 E_2 , E_2 E_3 , E_3 E_1 \] \[ E_1 E_2 E_3 \] (statt \(E_3 E_1\) könnten wir auch \(E_1 E_3\) als Basiselement nehmen – ist Geschmackssache, denn es ändert sich ja nur ein Vorzeichen).
Jedes Element (jedes Produkt) der Clifford-Algebra des \( \mathbb{R}^3 \) lässt sich in eine Linearkombination dieser 8 Basis-Produkte mit reellen Koeffizienten entwickeln. Genau so ist es auch bei einer äußeren Algebra oder bei Differentialformen. Allgemein gibt es bei einem n-dimensionalen Vektorraum in der zugehörigen Clifford-Algebra \(2^n\) solche Basis-Produkte, und zwar jeweils \(n\) über \(k\) Basis-Produkte mit \(k\) Generatoren.
Die obigen Formeln zeigen eine große Ähnlichkeit mit den Formeln, die wir von Differentialformen her kennen (siehe Kapitel 5.1.11 ). Kann man vielleicht beispielsweise das Produkt \( E_1 E_2 \) mit einer Fläche in Beziehung setzen? Man kann! Wir schauen uns das weiter unten noch genauer an (Stichwort: geometrische Algebra).
Wie sieht es mit der Eindeutigkeit einer Clifford-Algebra aus? Angenommen, wir starten mit dem Vektorraum \(V\) mit Metrik \(g\) und betrachten neben der Abbildung \(j\) noch eine andere Abbildung \(j'\), die ebenfalls die universelle Eigenschaft erfüllt. Anders gesagt: wir betrachten neben den Generator-Matrizen \(E_\mu\) noch andere Generator-Matrizen \(E_\mu'\), deren Antikommutator ebenfalls die metrische Matrix ergibt. Dann gibt es eine Umrechnungs-Abbildung \( ( )' \) (einen Algebrenmorphismus), mit der man die eine Darstellung in die andere umrechnen kann und die mit dem Algebra-Produkt und der Vektorraumstruktur verträglich ist. Physiker würden beispielsweise einfach schreiben: \( (X Y)' = X' Y' \). Man kann erst multiplizieren und dann das Ergebnis in die andere Darstellung umrechnen, oder man kann auch gleich in die andere Darstellung umrechnen und dort multiplizieren – es ist egal. In diesem Sinn sind verschiedene Darstellungen der Clifford-Algebra gleichwertig und die Clifford-Algebra ist eindeutig festgelegt. Physiker kennen das: Es gibt verschiedene Darstellungen für die Dirac-Matrizen, aber es ist letztlich egal, welche man verwendet. Hauptsache, ihr Antikommutator ergibt die Minkowski-Metrik. Das ist ein Grund mehr, möglichst lange auf eine konkrete Matrixdarstellung zu verzichten und eine abstraktere Formulierung zu verwenden.
Allgemein kann man zeigen, dass man jede Clifford-Algebra durch Matrizen oder Paare von Matrizen darstellen kann, deren Matrixelemente reelle Zahlen, komplexe Zahlen oder Quaternionen sind (siehe z.B. Wikipedia: Clifford-Algebra). Es gibt mehrere Methoden, wie man die Matrizen konstruieren kann, wobei es wichtig ist, ob der Vektorraum \(V\) gerade oder ungerade Dimension besitzt.. Das geht bei gerader Dimension beispielsweise über Leitermatrizen, ähnlich den Leiteroperatoren bei der Drehimpuls-Algebra. Siehe z.B. Wikipedia: Classification of Clifford algebras und Wikipedia: Clifford module.
Wenn man eine Matrixdarstellung hat, so ist eine Umrechnungs-Abbildung \( ( )' \) über Ähnlichkeitstransformationen gegeben: \[ E_\mu' := S E_\mu S^{-1} \] mit einer invertierbaren Matrix \(S\). Man kann leicht nachprüfen, dass auch die Matrizen \(E_\mu'\) die universelle Eigenschaft erfüllen: Multiplizieren wir \[ E_\mu E_\nu + E_\nu E_\mu = 2 g_{\mu\nu} \] von links mit \(S\) und von rechts mit \(S^{-1}\) und fügen zwischen den Generatoren die Identität \( 1 = S^{-1} S \) ein, so ergibt das \[ S E_\mu S^{-1} S E_\nu S^{-1} + S E_\nu S^{-1} S E_\mu S^{-1} = \] \[ = 2 S g_{\mu\nu} S^{-1} \] und damit ( \(g_{\mu\nu}\) ist ja nur eine Zahl für festes \(\mu\) und \(\nu\) und keine Clifford-Matrix) \[ E_\mu' E_\nu' + E_\nu' E_\mu' = 2 g_{\mu\nu} \] So, damit wäre das Wichtigste über Clifford-Algebren gesagt. Schauen wir uns einige Beispiele an, die zeigen, dass wir es hier mit einem sehr allgemeinen, mächtigen und universell verwendbaren Begriff zu tun haben.
Betrachten wir als einfaches Beispiel den eindimensionalen reellen Vektorraum \[ V = \mathbb{R} \] mit der normalen euklidischen Metrik \[ g_{11} = 1 \] Da es nur einen Basisvektor von \(V\) gibt (nennen wir ihn \( \boldsymbol{e}\)), gibt es auch nur einen Clifford-Generator \(E\) und aus der universellen Eigenschaft folgt \[ E E = 1 \] Die beiden Basiselemente der Clifford-Algebra lauten also \(1\) und \(E\). Eine Matrixdarstellung wäre die \(2-mal-2\)-Einheitsmatrix (die wir auch \( \sigma_0 \) genannt hatten) für \(1\) sowie eine der drei Pauli-Matrizen für \(E\) . Nehmen wir konkret die Diagonalmatrix \( \sigma_3 \) mit 1 und -1 als Diagonalelemente: \[ 1 = \sigma_0 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \] \[ E = \sigma_3 = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \] Diese Basis der Clifford-Algebra besteht somit nur aus Diagonalmatrizen, die beim Multiplizieren auch diagonal bleiben. Es genügt daher, nur die Diagonalelemente zu betrachten und kurz \[ 1 = (1,1) \] \[ E = (1,-1) \] zu schreiben. Es bietet sich nun an, zu einer neuen Basis überzugehen: \[ B := 1 + E = (1,0) \] \[ B' := 1 - E = (0,1) \] Ein allgemeines Element \(A\) der Clifford-Algebra können wir dann schreiben als \[ A = a B + a' B' = (a,a') \] Das Produkt zweier solcher Elemente wäre dann \[ A C = (a c, a' c') \] d.h. es wird komponentenweise multipliziert. Diese Cliffordalgebra kann also als Algebra durch die direkte Summe \( \mathbb{R} \oplus \mathbb{R} \) dargestellt werden mit der reellen Multiplikation zwischen reellen Zahlen als Algebra-Produkt. Man könnte auch sagen: Sie ist als Algebra darstellbar durch die Matrixalgebra der reellen 2-mal-2-Diagonalmatrizen. Diese Clifford-Algebra bietet nicht viel Neues – man braucht sie nicht wirklich. Bei mehr Dimensionen mit euklidischer Metrik wird es interessanter, denn die verschiedenen Generatoren müssen ja antivertauschen. Mehr dazu später.
Bei \(V = \mathbb{R}\) wird es
auch interessanter, wenn wir
\[ g_{11} = - 1 \]
verwenden,
so dass
\[ E E = -1 \]
ist.
Als Matrixalgebra-Basis könnten wir die 2-mal-2-Einheitsmatrix \(1\) und
\( -i \sigma_2 \) für \(E\) wählen:
\[
1 = \sigma_0 =
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
\]
\[
E = -i \sigma_2 =
\begin{pmatrix}
0 & -1 \\
1 & 0
\end{pmatrix}
\]
Das ergibt die Matrixdarstellung der komplexen Zahlen, die in
Kapitel 6.1 gezeigt wird.
Einfacher können wir auch das Clifford-Algebra-Element
\( x 1 + y E \) direkt durch die komplexen Zahl
\( x + i y \) darstellen, d.h. \(E\) entspricht der imaginären Einheit \(i\).
Kurz gesagt: Diese Clifford-Algebra entspricht den komplexen Zahlen.
Weiten wir den Fall mit den komplexen Zahlen um eine Dimension aus und betrachten \[ V = \mathbb{R}^2 \] mit \[ g_{11} = g_{22} = - 1 \] Hier haben wir zwei Generatoren \(E_1\) und \(E_2\) mit \[ E_1 E_1 = E_2 E_2 = -1 \] \[ E_1 E_2 = - E_2 E_1 \] Die vier Basiselemente der Clifford-Algebra lauten \[ 1 , \, E_1 , \, E_2, \, E_1 E_2 \] Quadriert man das vierte Basiselement \(E_1 E_2\), so erhält man \[ (E_1 E_2)^2 = \] \[ = E_1 E_2 E_1 E_2 = \] \[ = - E_1 E_1 E_2 E_2 = \] \[ = - (-1) (-1) = \] \[ = -1 \] d.h. auch für das vierte Basiselement ist das Quadrat gleich \(-1\), so wie beim zweiten und dritten Basiselement (nicht aber beim ersten Basiselement).
Man hat es hier mit einer Art Erweiterung der komplexen Zahlen zu tun, bei der es drei imaginäre Einheiten gibt, die man auch oft mit \(i, j, k\) bezeichnet. Dies ist genau die Struktur der sogenannten Quaternionen. Eine Matrixdarstellung bilden die Produkte aus 2 Paulimatrizen (z.B. \( E_1 = \sigma_1 \sigma_2 \)) usw.. Alternativ kann man auch die mit \(-i\) multiplizierten Paulimatrizen nehmen, z.B. \(E_1 = -i \sigma_3\). Interessant ist, dass die Quaternionen wie die komplexen Zahlen eine Divisionsalgebra bilden, d.h. es gibt immer ein multiplikativ inverses Element in der Algebra. Bei der Algebra der Pauli-Matrizen stimmt das nicht. Zur Verdeutlichung sind hier noch einmal die Pauli-Matrizen:
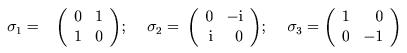
Die Formel \(E_1 = -i \sigma_3\) legt nahe, dass wir die Algebra der Paulimatrizen (also ohne das \(-i\))
erhalten könnten, wenn wir bei \(V = \mathbb{R}^2\) diesmal
die euklidische Metrik
\[
g_{11} = g_{22} = 1
\]
verwenden.
Hier gilt für die Quadrate der zwei Generatoren \(E_1\) und \(E_2\) die Formel
\[
E_1 E_1 = E_2 E_2 = 1
\]
sowie wie zuvor
\[
E_1 E_2 = - E_2 E_1
\]
Die vier Basiselemente der Clifford-Algebra lauten wieder
\[
1 , \, E_1 , \, E_2, \, E_1 E_2
\]
Quadriert man hier das vierte Basiselement \(E_1 E_2\), so erhält man
\[
(E_1 E_2)^2 =
\]
\[ =
E_1 E_2 E_1 E_2 =
\]
\[ =
- E_1 E_1 E_2 E_2 =
\]
\[ =
- 1 1 =
\]
\[ = -1
\]
d.h. für das vierte Basiselement ist das Quadrat gleich \(-1\)
so wie beim ersten Basiselement (der \(1\)) und anders als beim zweiten und dritten Basiselemet.
Das Quadrat der Pauli-Matrizen ist aber immer 1, d.h. die Pauli-Matrizen sind keine Matrixdarstellung dieser Clifford-Algebra. Eine Matrixdarstellung ist dagegen durch die folgenden reellen Matrizen gegeben: \[ E_1 = \sigma_3 \] \[ E_2 = \sigma_1 \] \[ E_1 E_2 = \sigma_3 \sigma_1 = i \sigma_2 \] Zusammen mit der Einheitsmatrix bilden diese 4 Matrizen eine Basis für alle reellen 2-mal-2-Matrizen, d.h. die Clifford-Algebra kann hier durch die reellen 2-mal-2-Matrizen dargestellt werden.
Schauen wir uns noch den gemischten Fall
\[
g_{11} = 1
\]
\[
g_{22} = -1
\]
an.
Es gilt also
\[
E_1 E_1 = 1
\]
\[
E_2 E_2 = -1
\]
\[
E_1 E_2 = - E_2 E_1
\]
Quadriert man hier das vierte Basiselement \(E_1 E_2\), so erhält man
\[
(E_1 E_2)^2 =
\]
\[ =
E_1 E_2 E_1 E_2 =
\]
\[
- E_1 E_1 E_2 E_2 =
\]
\[ =
- 1 (-1) =
\]
\[ = 1
\]
Vergleicht man mit dem vorherigen Fall, so sieht man, dass nur die Rollen von \(E_2\)
und \(E_1 E_2\) vertauscht sind. Eine Matrixdarstellung ist daher
\[
E_1 = \sigma_3
\]
\[
E_2 = i \sigma_2
\]
\[
E_1 E_2 = \sigma_3 \, i \sigma_2 = \sigma_1
\]
d.h. die Clifford-Algebra kann wieder durch die reellen 2-mal-2-Matrizen dargestellt werden.
Im eindimensionalen wie im zweidimensionalen reellen Fall ist also eigentlich nur die negative euklidische Metrik interessant, die die komplexen Zahlen sowie deren Erweiterung (die Quaternionen) hervorbringt.
Noch eine Anmerkung:
Wir haben gesehen, dass die Clifford-Algebren für den zweidimensionalen euklidischen Fall und den gemischten Fall \( g_{11} = 1 \) und \( g_{22} = -1 \) beide durch die reellen 2-mal-2-Matrizen dargestellt werden können. Dennoch sind die beiden Clifford-Algebren keineswegs identisch! Als assoziative Algebren sind beide darstellbar durch die reellen 2-mal-2-Matrizen, denn diese Matrizen ergeben die richtige Produktstruktur. Die Clifford-Algebren enthalten aber noch eine zusätzliche Information, die die reellen 2-mal-2-Matrizen nicht enthalten: Über die Abbildung \( X = j(x) \) wird in den Matrizen ein Unterraum identifiziert, der die Einbettung des Vektorraums (zusammen mit seiner Metrik) in die Algebra darstellt. Das ist bei den beiden Clifford-Algebren jeweils ein anderer Unterraum, denn die Metrik des Vektorraums ist jeweils verschieden. Hier ein entsprechendes Zitat aus Pertti Lounesto: Counterexamples to theorems published and proved in recent literature on Clifford algebras, spinors, spin groups and the exterior algebra für den zweidimensionalen euklidischen Fall:
In comparing Cl2 and Mat(2,R), which are isomorphic as associative algebras, it should be noted that Cl2 has more structure: in the Clifford algebra Cl2 there is a distinguished subspace, isometric to the Euclidean plane R2. No such privileged subspace exist in Mat(2,R).
Diese Anmerkung betrifft alle hier betrachteten Matrixdarstellungen von Clifford-Algebren.
Für die negative euklidische Metrik erhalten wir wieder im Wesentlichen die Quaternionen wie schon im zweidimensionalen Fall. Genauer müsste man sagen: Wir haben es mit den Biquaternionen zu tun (mehr dazu unter dem angegebenen Wikipedia-Link).
Für die positive euklidische Metrik erhalten wir dagegen endlich die Algebra der Pauli-Matrizen. Zusammen mit der Einheitsmatrix bilden diese Matrizen und ihre Produkte eine Basis der komplexen 2-mal-2-Matrizen, d.h. die Clifford-Algebra ist darstellbar durch die Algebra der komplexen 2-mal-2-Matrizen. Mehr dazu weiter unten beim Thema Spin-Gruppen.
Die gemischten Fälle wollen wir hier nicht weiter betrachten. Eine Übersicht folgt weiter unten.
Besonders interessant ist hier der Fall mit \(g_{11} = g_{22} = g{33} = 1 \) und \(g_{00} = -1 \). Mit dieser Metrik kann man die Raum-Zeit beschreiben (wir haben allerdings normalerweise genau die umgekehrten Vorzeichen verwendet). Der Vorteil dieser Vorzeichenkonvention ist, dass die reellen 4-mal-4-Matrizen eine Matrixdarstellung bilden, wobei man alle 16 Basismatrizen braucht. Komplexe Zahlen sind nicht nötig! Man spricht von der Majorana-Algebra.
Wählt man das umgekehrte Vorzeichen für die Raum-Zeit-Metrik, so wie wir das normalerweise hier machen, so braucht man entweder komplexe 4-mal-4-Matrizen (Dirac-Algebra) oder reelle 8-mal-8-Matrizen für eine Darstellung. Siehe auch Wikipedia: Representations of Clifford algebras. Mehr dazu wieder weiter unten beim Thema Spin-Gruppen
Infos dazu finden Sie beispielsweise in Wikipedia: Classification of Clifford algebras.
Zurück zu unserem roten Faden von ganz oben:
...
Mathematically, there is a
close relation between spinors and reflections ...
...
The best way to talk about spinors and reflections is, once again,
Clifford algebra ....
Was Clifford-Algebren sind, wissen wir nun. Offenbar haben sie etwas mit Reflexionen (Spiegelungen an einer Hyperebene) zu tun. Und Spiegelungen werden uns dann in einem weiteren Schritt schließlich zu Drehungen oder Lorentz-Transformationen führen (zwei räumliche Spiegelungen an verschiedenen Ebenen ergeben eine Drehung – Details kommen noch).
Starten wir wieder mit dem reellen n-dimensionalen Vektorrraum \(V\) mit Metrik \(g\). Für die Spiegelung brauchen wir eine \(n-1\) -dimensionale Hyperebene \(H\), an der wir spiegeln können (so ist das Wort Spiegelung hier gemeint). Eine solche Hyperebene \(H\) können wir durch einen Normalenvektor \(e\) kennzeichnen, der senkrecht zu \(H\) liegt: Jeder Vektor \(h\) aus der Hyperebene \(H\) steht senkrecht zu \(e\), d.h. \[ g(e,h) = 0 \] (man beachte, dass \(H\) durch den Ursprung geht, wenn man den Normalenvektor \(e\) anschaulich vom Ursprung ausgehen lässt).
Die anschauliche Bedeutung von senkrecht gilt natürlich nur für eine euklidische Metrik. Genauso wird es mit dem Begriff Spiegelung sein. Den Normalenvektor \(e\) wollen wir auf \(1\) in Bezug auf die gegebene Metrik normieren, d.h. \[ |g(e,e)| = 1 \] Damit sind beispielsweise für die Minkowski-Raumzeit lichtartige Vektoren für \(e\) ausgeschlossen: \(e\) ist entweder zeitartig und \(H\) damit raumartig oder umgekehrt. Spiegelungen an einer lichtartigen Hyperebene werden nicht betrachtet (sie sind über die Metrik auch nicht direkt definierbar, denn jeder lichtartige Vektor ist senkrecht zu sich selbst, hat also Metrik Null).
Wir wollen nun einen Vektor \(x\) an der Hyperebene \(H\) spiegeln. Gemeint ist damit für eine euklidische Metrik: Wir wollen die Komponente von \(x\), die senkrecht zur Hyperebene (also parallel zum Normalenvektor \(e\)) liegt, invertieren (es spielt also nur die Ausrichtung der Hyperebene eine Rolle, oder anders gesagt: die Ebene muss durch den Ursprung gehen, wenn wir die Vektoren als Ortsvektoren des \(\mathbb{R}^n\) auffassen). Für eine allgemeine nichteuklidische Metrik werden wir dann diese Definition geeignet verallgemeinern.
Die Spiegelung wollen wir mit Hilfe der Clifford-Algebra formulieren. Dazu übersetzen wir \(x\) und den Normalenvektor \(e\) in die Clifford-Algebra und erhalten \(X\) und \(E\). Insbesondere ist dann \[ E E = g(e,e) \] und damit auch \[ E^{-1} = E \, \frac{1}{g(e,e)} \] Nun berechnen wir das Produkt \[ X' := \] \[ = - E X E^{-1} = \] \[ = - E X E \, \frac{1}{g(e,e)} \] (diese Konvention entspricht der Notation in Chris Doran: Geometric Algebra and its Application to Mathematical Physics, Chapter 3 (Gleichung 3.7) – hier findet man viele weitere Infos zu dem Thema).
Das Produkt der ersten beiden Faktoren \( E X \) ist aufgrund der universellen Eigenschaft der Clifford-Algebra \( E X + X E = 2 \, g(e,x) \) gegeben durch \[ E X = 2 \, g(e,x) - X E \] d.h. wir haben \[ X' := \] \[ = - E X E^{-1} = \] \[ = - E X E \, \frac{1}{g(e,e)} = \] \[ = - ( \, 2 g(e,x) - X E ) \, E \, \frac{1}{g(e,e)} = \] \[ = - 2 \, \frac{g(e,x)}{g(e,e)} \, E + X \, \frac{g(e,e)}{g(e,e)} = \] \[ = X - 2 \, \frac{g(e,x)}{g(e,e)} \, E \]
Wir können nun \(X'\) wieder in einen Vektor \(x'\) zurückübersetzen, denn rechts stehen zwei Terme,
die sich ebenfalls zurückübersetzen lassen.
(die Abbildung \(j^{-1}\) ist ja wie \(j\) linear).
Es ist also
\[
x' =
\]
\[ = j^{-1}(- E X E^{-1}) =
\]
\[
= x - 2 \, \frac{g(e,x)}{g(e,e)} \, e
\]
Im euklidischen Fall mit \( g(e,e) = 1 \) ist \( g(e,x) \, e \)
gerade die Projektion von \(x\) auf den Normalenvektor \(e\). Diese Projektion wird zweimal abgezogen,
so dass \( x' \) gerade die umgekehrte Projektion
auf \(e\) besitzt. Der Vektor \( x' \) ist damit der an der Hyperebene
gespiegelte Vektor.
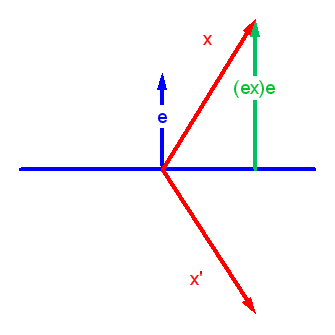
Die Division durch \(g(e,e)\) bewirkt, dass die Formel auch für die vierdimensionale Raumzeit mit der Minkowski-Metrik für die räumlichen Komponenten passt: Wenn bei \(x\) und \(e\) die Null-Komponente verschwindet (also \( x = (0, \boldsymbol{x}) \) und \( e = (0, \boldsymbol{e}) \)), so folgt \( x' = (0, \boldsymbol{x}') \) sowie \( g(e,x) = - \boldsymbol{e x} \) und \( g(e,e) = - \boldsymbol{e e} = - 1 \). Damit ist \[ x' = \begin{pmatrix} 0 \\ \boldsymbol{x}' \end{pmatrix} = \] \[ = x - 2 \, \frac{g(e,x)}{g(e,e)} \, e = \] \[ = \begin{pmatrix} 0 \\ \boldsymbol{x} \end{pmatrix} - 2 \, (\boldsymbol{e x}) \, \begin{pmatrix} 0 \\ \boldsymbol{e} \end{pmatrix} \] d.h. \[ \boldsymbol{x}' = \boldsymbol{x} - 2 \, (\boldsymbol{e x}) \, \boldsymbol{e} \] ist die Spiegelung von \(\boldsymbol{x}\) an der Hyperebene mit dem richtigen Vorzeichen.
Halten wir fest:
|
Spiegelung an der Hyperebene bei allgemeiner Metrik: Die Gleichung \[ x' = j^{-1}(X') = \] \[ = j^{-1}(- E X E^{-1}) = \] \[ = x - 2 \, \frac{g(e,x)}{g(e,e)} \, e \] definiert eine Spiegelung an einer Hyperebene \(H\) bei allgemeiner Metrik. Dabei ist \(e\) der Normalen-Einheitsvektor der Hyperebene, d.h. \(|g(e,e)| = 1\) und \(g(e,h) = 0\) für jeden Vektor \(h\) aus der Hyperebene \(H\) (\(e\) steht in diesem Sinn senkrecht auf der Hyperebene). Im euklidischen Fall und im Minkowski-Fall (für die räumlichen Komponenten) liefert die Formel das anschaulich erwartete Ergebnis. Im allgemeinen Fall betrachten wir sie als Definition des Begriffs Spiegelung.
|
Die oben definierte Spiegelung verändert die Metrik zwischen Vektoren nicht: \[ 2 \, g(a',b') = \] \[ A'B' + B'A' = \] \[ = (- E A E^{-1}) \, (- E B E^{-1}) + \] \[ + (- E B E^{-1}) \, (- E A E^{-1}) = \] \[ = E A B E^{-1} + E B A E^{-1} = \] \[ = E \, (A B + B A) \, E^{-1} = \] \[ = E \, 2 \, g(a,b) \, E^{-1} = \] \[ = 2 \, g(a,b) \] d.h. die Spiegelung ist eine orthogonale Abbildung (bezogen auf die Metrik \(g\)). Die obige Rechnung zeigt im Übrigen, dass es sich in der Clifford-Algebra sehr gut rechnen lässt – oft besser als direkt mit Vektoren oder Tensoren. Dieser Punkt wird von den Vertretern der Geometrischen Algebra immer wieder betont (siehe auch weiter unten).
Zwei Spiegelungen an verschiedenen Hyperebenen ergeben zusammen natürlich auch wieder eine orthogonale Abbildung – sogar eine speziell-orthogonale Abbildung, d.h. die Orientierung (rechts-links) bleibt erhalten.
Nennen wir den Normalenvektor für die erste Spiegelung
\(e\) und für die zweite Spiegelung
\(e'\) (hat nichts mit der Schreibweise \(x'\) zu tun).
Bei euklidischer Metrik (oder bei Minkowski-Metrik für die räumlichen Komponenten)
ergibt sich so eine Drehung – dabei
ist der Winkel, der zwischen den beiden Hyperebenen (und damit zwischen \(e\) und \(e'\)) liegt,
gerade der halbe Drehwinkel.
Die folgende Grafik zeigt das anschaulich am zweidimensionalen euklidischen Fall:
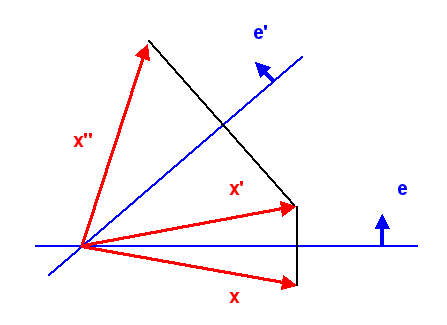
Umgekehrt lässt sich jede orthogonale Abbildung in ein Produkt aus Spiegelungen zerlegen (bei speziell-orthogonalen Abbildungen in eine gerade Zahl von Spiegelungen, typischerweise 2 davon, wenn man sie geeignet wählt). Bei Drehungen ist der Beweis anschaulich klar: Man wählt zwei Hyperebenen, die den halben Drehwinkel einschließen. Aber auch bei einer Lorentztransformation gilt der Satz: auch sie lassen sich als ein gerades Produkt von unseren verallgemeinerten Spiegelungen schreiben, wie wir sie oben definiert haben.
Bei zwei Spiegelungen mit Normalenvektor \(e\) und \(e'\) macht die erste Spiegelung aus \(X\) das Element \( - E X E^{-1} \) und die zweite Spiegelung daraus das Element \[ X' = E' E X E^{-1} E'^{-1} \] (wir verzichten hier auf den zweiten Strich \(X''\), da wir immer die zweifache Spiegelung betrachten, ohne den Zwischenschritt separat aufzuführen).
Schreiben wir \[ R := E' E \] so haben wir damit \[ X' = R X R^{-1} \] Da die zweifache Spiegelung eine speziell-orthogonale Abbildung ist, muss es eine speziell-orthogonale Matrix \( \boldsymbol{R} \) geben, so dass \( x' = \boldsymbol{R} x \) ist (wir schreiben die Matrix \( \boldsymbol{R} \) in Fettdruck, um sie vom Clifford-Algebra-Element \(R\) zu unterscheiden). Schreiben wir wieder \( X = j(x) \) und \( X' = j(x') \), so bedeutet das:
| \[ j(\boldsymbol{R} x) = R \, j(x) \, R^{-1} \] |
Diese Gleichung ist die Verallgemeinerung von Gleichungen wie \[ \sigma(\Lambda x) = g \, \sigma(x) \, g^+ \] wie wir sie von oben kennen. Wir kommen unten noch darauf zurück (z.B. was \(g^+\) mit \(R^{-1}\) zu tun hat).
Bei mehrfachen Spiegelungen treten Produkte wie \( E E' \) auf. Deshalb definiert man die sogenannte Pin-Gruppe. Sie ist die Gruppe aller Clifford-Algebra-Elemente, die man als Produkt mehrerer Einheits-Cliffordalgebra-Vektoren \(E, E', \, ... \) schreiben kann, wobei \( |E E| = 1 , \, |E' E'| = 1 \) usw. gilt (d.h. die entsprechenden Vektoren sind Einheitsvektoren mit \( |g(e,e)| = 1 , \, |g(e',e')| = 1 \) usw.).
\(R\) ist also ein Element der Pin-Gruppe. Allgemein gilt: Wenn \(R\) ein Element der Pin-Gruppe ist, so ist die über \[ j(\boldsymbol{R} x) = R \, j(x) \, R^{-1} \] definierte Abbildung \(\boldsymbol{R}\) orthogonal (aber nicht unbedingt speziell orthogonal, denn Spiegelungen gehen auch). Dabei ergeben \(R\) und \(-R\) dasselbe \(\boldsymbol{R}\). Man sagt, die Pin-Gruppe wird surjektiv in doppelter Überlagerung auf die orthogonalen Abbildungen von \(V\) abgebildet (siehe Wikipedia: Clifford-Algebra ).
Wie wir gesehen haben, ergeben im euklidischen Raum zwei Spiegelungen eine Drehung, also eine speziell-orthogonale Abbildung. Entsprechend interessiert man sich besonders für die Produkte mit einer geraden Anzahl von Einheits-Cliffordalgebra-Vektoren. Diese Untergruppe der Pin-Gruppe nennt man Spin-Gruppe (stammt vom Wortspiel spezielle Pin-Gruppe). Oft bezeichnet man \(R\) auch als Rotor und die Spin-Gruppe als Rotor-Gruppe.
Analog zur Pin-Gruppe gilt: Wenn \(R\) ein Element der Spin-Gruppe ist, so ist die über \( j(\boldsymbol{R} x) = R \, j(x) \, R^{-1} \) definierte Abbildung \(\boldsymbol{R}\) speziell orthogonal (d.h. Spiegelungen gehen nicht).
Dabei ergeben wieder \(R\) und \(-R\) dasselbe \(\boldsymbol{R}\), d.h. die Spin-Gruppe wird surjektiv in doppelter Überlagerung auf die speziell-orthogonalen Abbildungen von \(V\) abgebildet (wobei der Begriff speziell-orthogonal über die Metrik von \(V\) definiert ist).
Weiterhin weiß man, dass bei euklidischer Metrik ab 3 reellen Dimensionen (und glücklicherweise auch bei Minkowski-Metrik) die Spin-Gruppe einfach zusammenhängend ist, d.h. sie ist die universelle Überlagerungsgruppe der speziell-orthogonalen Gruppe, so wie man sie in der Quantentheorie braucht (siehe Wikipedia: Clifford-Algebra ).
Bei allgemeiner nicht-euklidischer Metrik wird die Sache komplizierter. Die Spingruppe ist dann i.a. nicht mehr die universelle Überlagerungsgruppe, denn man kann zeigen, dass die universelle Überlagerungsgruppe nun eine vierfache Überdeckung der speziell-orthogonalen Gruppe ist, während die Spingruppe nur eine doppelte Überdeckung liefert. Die universelle Überlagerungsgruppe überdeckt ihrerseits die Spingruppe doppelt. Mehr dazu siehe John Baez: Spin groups for indefinite metrics. Hier ein Zitat daraus für Experten:
The fundamental group of the special orthogonal group SO(p,q) depends
on p and q. (throughout, I really mean the connected component of the
identity.) If q = 0 or 1, and p > 2, it's well known that the
fundamental group is just Z_2. However (this is the case I'm interested
in for now), if both p and q > 2, say SO(3,3), then the fundamental
group is Z_2 x Z_2.
...
Next, when we define the spinor group Spin(p,q), it turns out to be a
double cover of SO(p,q) - I'm thinking here of the construction of the
spinor group via Clifford modules, etc. However, for p,q > 2, Spin(p,q)
is not the universal covering group of SO(p,q) - the universal cover
would have to be a four fold cover!
Ein Beispiel: die Spingruppe \(Spin(3,3)\) (d.h. \(V = \mathbb{R}^6\) mit drei positiven und drei negativen Einsen in der Diagonalen der metrischen Matrix) ist nicht einfach zusammenhängend, wie es die universelle Überlagerungsgruppe sein müsste (siehe beispielsweise Pertti Lounesto: Counterexamples to theorems published and proved in recent literature on Clifford algebras, spinors, spin groups and the exterior algebra).
Wie konstruiert man nun die Rotoren \(R\) und damit die Spingruppe? Wenn die Metrik positiv definit ist, kann man jeden Rotor \(R\) in der Form
| \[ R = e^{B/2} \] mit \[ B = \sum_{\mu \lt \nu} \, \alpha^{\mu\nu} E_\mu E_\nu \] |
Man sagt auch, \(B\) ist ein Clifford-Bivektor (so wie \( X := j(x) \) ein Clifford-Vektor ist). Dabei ist \(B\) nicht unbedingt eindeutig bestimmt. Mehr dazu siehe beispielsweise in Chris Doran: Geometric Algebra and its Application to Mathematical Physics, Chapter 3.
Ist die Metrik nicht positiv definit (wie z.B. die Minkowski-Metrik), dann kann nicht jeder Rotor so geschrieben werden. So kann beispielsweise der Fall auftreten, dass man zwar einen bestimmten Rotor \(R\) so schreiben kann, nicht aber den Rotor \(-R\). Dieser Fall tritt beispielsweise bei der Gruppe \(SL(2,\mathbb{C})\) auf (siehe am Schluss von Kapitel 4.10). In der Nähe der \(1\) kann man aber immer \( R = e^{B/2} \) schreiben.
Wenden wir unser neu erworbenes Wissen auf ein Beispiel an, bei dem wir uns von früheren Kapiteln her bestens auskennen: die Drehgruppe \(SO(3)\). \(V\) ist also gleich \(\mathbb{R}^3\) mit euklidischer Metrik. Enstprechend schreiben wir wie gewohnt lateinische statt griechische Indices, Vektoren schreiben wir mit fetten Buchstaben (z.B. \( \boldsymbol{x} \)), es ist \( g_{ij} = \delta_{ij} \) und wir schreiben \( g(x,y) = \boldsymbol{xy} \), d.h. die Metrik ist gleich dem euklidischen Skalarprodukt.
Von oben wissen wir, dass wir die Clifford-Algebra in diesem Fall durch die Algebra der Pauli-Matrizen darstellen können. Die Clifford-Generatoren \(E_i\) lassen sich also durch die drei Pauli-Matrizen \(\sigma_i\) darstellen, denn diese erfüllen die Beziehung \[ \sigma_i \sigma_j + \sigma_j \sigma_i = 2 \, \delta_{ij} \] Zusammen mit der Einheitsmatrix bilden diese Matrizen und ihre Produkte eine Basis der komplexen 2-mal-2-Matrizen, d.h. die Clifford-Algebra ist durch die Algebra der komplexen 2-mal-2-Matrizen \(\mathbb{C}(2)\) darstellbar.
Nun zur Gleichung \[ j(\boldsymbol{R} x) = R \, j(x) \, R^{-1} \] die den Rotor \(R\) der Spingruppe mit der Matrix \(\boldsymbol{R}\) aus \(SO(3)\) verknüpft. Diese Gleichung können wir leicht in die uns bekannte Beziehung zwischen \(SU(2)\) und \(SO(3)\) überführen, indem wir \[ j(\boldsymbol{x}) = x^i E_i = x^i \sigma_i = \sigma(\boldsymbol{x}) \] schreiben, statt \(R\) den Buchstaben \(u\) für den Rotor verwenden sowie statt \(\boldsymbol{R}\) den Buchstaben \(R\) für die Drehmatrix aus \(SO(3)\) schreiben. Damit ergibt sich \[ \sigma(R\boldsymbol{x}) = u \, \sigma(\boldsymbol{x}) \, u^{-1} \] Da die Metrik positiv definit ist, kann man nach oben den Rotor \(u\) in der Form \[ u = e^{B/2} \] schreiben, wobei \(B\) in der Form \[ B = \sum_{m \lt n} \, \alpha^{mn} \sigma_m \sigma_n \] geschrieben werden kann. Wenn wir \( \alpha^{mn} \) antisymmetrisch in den Indices wählen, dann kann man diese Summe auch schreiben als \[ B = \] \[ = \alpha^{12} \sigma_1 \sigma_2 + \] \[ + \alpha^{23} \sigma_2 \sigma_3 + \] \[ + \alpha^{31} \sigma_3 \sigma_1 \] Für die Pauli-Matrizen gilt nun \[ \sigma_1 \sigma_2 = i \sigma_3 \] (analog mit zyklisch vertauschten Indices), d.h. wir haben \[ B = \] \[ = \alpha^{12} \, i \sigma_3 + \] \[ + \alpha^{23} \, i \sigma_1 + \] \[ + \alpha^{31} \, i \sigma_2 \] Nun setzen wir noch \( \alpha^{12} =: - w_3 \) (usw. zyklisch), so dass \[ B = - i \, \sigma(\boldsymbol{w}) \] wird. Damit haben wir
|
\[
u = e^{- i \, \sigma(\boldsymbol{w})/2}
\]
|
Das ist genau die Darstellung für eine \(SU(2)\)-Matrix aus Kapitel 4.8 . Da für eine \(SU(2)\)-Matrix zudem noch \( u^{-1} = u^+ \) gilt, haben wir als Ergebnis
| \[ \sigma(R\boldsymbol{x}) = u \, \sigma(\boldsymbol{x}) \, u^+ \] |
Damit haben wir unser Ziel erreicht und den Zusammenhang zwischen \(SO(3)\) und der Überlagerungsgruppe (gleich Spingruppe) \(SU(2)\) aus Kapitel 4.8 hergeleitet! Außerdem haben wir gezeigt, dass die Spingruppe von \(SO(3)\) tatsächlich die Gruppe \(SU(2)\) ist.
Versuchen wir, analog die Spingruppe der Lorentzgruppe zu finden. \(V\) ist dabei gleich \( \mathbb{R}^4 \) mit der Minkowski-Metrik, d.h. \[ g(x,y) = x^0 y^0 - \boldsymbol{x y} \] Von oben (Tabelle zum allgemeinen Fall) wissen wir, dass die Clifford-Algebra in diesem Fall durch \( \mathbb{H}(2) \) dargestellt werden kann, also durch 2-mal-2-Matrizen mit Quaternionen als Matrixelemente.
Die Quaternionen kennen wir von oben als Clifford-Algebra des \( \mathbb{R}^2 \) mit negativer euklidischer Metrik. Die beiden Generatoren lauten \( I \) und \( J \) mit \[ I^2 = J^2 = - 1 \] \[ I J = - J I \] (oben hatten wir \( I = E_1 \) und \( J = E_2 \) geschrieben). Mit \( K := I J\) sind die Basiselemente dann \[ 1, \, I, \, J , \, K \] mit \[ I^2 = J^2 = K^2 = \] \[ = I J K = - 1 \] Eine Basis für reelle 2-mal-2-Matrizen bilden die reellen Matrizen \[ 1, \, \sigma_3, \, \sigma_1, \, i \sigma_2 \] mit \[ i \sigma_2 = \sigma_3 \sigma_1 \] (siehe oben die Clifford-Algebra zum euklidischen \( \mathbb{R}^2 \)). Die entsprechenden Clifford-Generatoren lauten \(\sigma_3\) und \(\sigma_1\).
Wie sehen nun die Clifford-Generatoren für \(\mathbb{R}^4\) mit Minkowski-Metrik aus? Das ist genau die Zusatzstruktur, die eine Clifford-Algebra besitzt und die man nicht direkt der darstellenden Matrixalgebra entnehmen kann (siehe den entsprechenden Kommentar weiter oben). Ein erster Versuch wäre es, einfach die 4 Generatoren von oben zu nehmen, also \[ I , \, J , \, \sigma_3 , \, \sigma_1 \] (wobei \(I\) und \(J\) mit der Einheitsmatrix multipliziert werden, was wir nicht extra hinschreiben). Dass man so tatsächlich eine Basis von \(\mathbb{H}(2)\) erhält, folgt einfach daraus, dass Produkte von \(1, I, J\) eine Basis der Quaternionen ergeben, und Produkte von \(1, \sigma_3, \sigma_1\) eine Basis der 4-mal-4-Matrizen ergeben.
Erfüllen die 4 Generatoren die universelle Eigenschaft? \(I\) und \(J\) antivertauschen, und \(\sigma_3\) und \(\sigma_1\) antivertauschen ebenfalls (wie das für Clifford-Generatoren auch sein muss). Leider vertauschen aber \(I\) bzw. \(J\) mit \(\sigma_3\) bzw. \(\sigma_1\) – sie müssten aber antivertauschen. Das können wir aber beheben, wenn wir \(I\) und \(J\) mit einer Matrix multiplizieren, die mit \(\sigma_3\) und \(\sigma_1\) antivertauscht. Dafür bietet sich die Matrix \( \sigma_3 \sigma_1 = i \sigma_2 \) an: \[ I i \sigma_2 , \, J i \sigma_2 , \, \sigma_3 , \, \sigma_1 \] Diese 4 Generatoren antivertauschen, und ihre Produkte bilden eine Basis von \(\mathbb{H}(2)\). So kann man \(I\) über das Produkt \[ (I i \sigma_2) \, \sigma_1 \, \sigma_3 = I i \sigma_2 (- i \sigma_2) = I \] zurückgewinnen (analog bei \(J\)). Bleibt noch die Frage, wie das Quadrat der einzelnen Generatoren aussieht, denn dieses muss ja gleich den Diagonalelementen der Minkowski-Metrik sein. Probieren wir es aus: \[ I i \sigma_2 \, I i \sigma_2 = (I I) \, (i i) \, (\sigma_2 \sigma_2) = 1 \] \[ J i \sigma_2 \, J i \sigma_2 = (J J) \, (i i) \, (\sigma_2 \sigma_2) = 1 \] \[ \sigma_3 \, \sigma_3 = 1 \] \[ \sigma_1 \, \sigma_1 = 1 \] Wir haben also die Generatoren für \( \mathbb{R}^4 \) mit euklidischer Metrik konstruiert. Aus der Tabelle oben sehen wir, dass die Clifford-Algebra in diesem Fall ebenfalls durch \( \mathbb{H}(2) \) dargestellt werden kann – das hat unsere Rechnung gerade bestätigt. Da wir aber die Generatoren für die Minkowski-Metrik haben wollen, brauchen wir noch eine kleine Änderung.
Kehren wir zurück zu den Generatoren \(I , \, J , \, \sigma_3 , \, \sigma_1 \). Sie hatten den Mangel, dass sie nicht alle antivertauschen. Statt nun \(I\) und \(J\) mit \( \sigma_3 \sigma_1 = i \sigma_2 \) zu multiplizieren, können wir den Mangel auch anders beheben: So können wir \( \sigma_1 \) mit \( K := I J \) multiplizieren und \(I\) und \(J\) mit \(\sigma_1\) multiplizieren: \[ I \sigma_1 , \, J \sigma_1 , \, \sigma_3 , \, K \sigma_1 \] Diese 4 Generatoren antivertauschen, und ihre Produkte bilden wieder eine Basis von \( \mathbb{H}(2) \). So erhält man \( \sigma_1 \)zurück, indem man das Produkt \[ - (I \sigma_1) \, (J \sigma_1) \, (K \sigma_1) = \sigma_1 \] bildet, und \(I\) erhält man über das Produkt \[ (J \sigma_1) \, (K \sigma_1) = J K = I \] zurück (analog \(J\)). Wie sieht es mit dem Quadrat der Generatoren aus? Da \[ I^2 = J^2 = K^2 = - 1 \] ist, und da \( \sigma_i^2 = 1 \) ist, haben wir genau unser gewünschtes Ergebnis: \[ \sigma_3^2 = 1 \] \[ (I \sigma_1)^2 = (J \sigma_1)^2 = (K \sigma_1)^2 = - 1 \] Wir können daher für die Generatoren der Clifford-Algebra der Minkowski-Raumzeit beispielsweise setzen:
| \[ E_0 := \sigma_3 \] \[ E_1 := J \sigma_1 \] \[ E_2 := K \sigma_1 \] \[ E_3 := I \sigma_1 \] |
(siehe mit etwas anderen Konventionen z.B. Markus Penz: Spaß mit Quaternionen, Feldtheorie-Seminar 2005 – die Nummerierung habe ich hier so gewählt, dass sie später mit den üblichen Konventionen für die Dirac-Matrizen zusammenpasst; es gibt aber hier viele Möglichkeiten). Hier sind die Matrizen noch einmal explizit ausgeschrieben: \[ E_0 = \sigma_3 = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \] \[ E_1 = J \sigma_1 = \begin{pmatrix} 0 & J \\ J & 0 \end{pmatrix} \] \[ E_2 = K \sigma_1 = \begin{pmatrix} 0 & K \\ K & 0 \end{pmatrix} \] \[ E_2 = I \sigma_1 = \begin{pmatrix} 0 & I \\ I & 0 \end{pmatrix} \] Diese Matrizen kann man in komplexwertige 4-mal-4-Matrizen übersetzen, indem man die Quaternionen I, J und K durch die folgenden komplexwertigen 2-mal-2-Matrizen ersetzt (siehe Wikipedia: Pauli-Matrizen , es gibt auch noch andere gleichwertige Möglichkeiten): \[ I = -i \sigma_3 \] \[ J = -i \sigma_1 \] \[ K = -i \sigma_2 \] Damit hätten wir \[ E_0 = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \] \[ E_k = \begin{pmatrix} 0 & -i \sigma_k \\ -i \sigma_k & 0 \end{pmatrix} \] mit \(k = 1, 2, 3 \) und der 2-mal-2-Einheitsmatrix \(1\) in \(E_0\).
Es gibt noch viele andere Matrixdarstellungen für diese Generatoren. So könnte man die Matrizen \[ \gamma_0 := E_0 \] \[ \gamma_k := i E_0 E_k \] definieren mit \(k = 1, 2, 3 \). Auch hier ist \[ \gamma_i \gamma_j = \] \[ = - E_0 E_i E_0 E_j = \] \[ = E_i E_0 E_0 E_j = \] \[ = E_i E_j \] sowie \[ \gamma_0 \gamma_k = \] \[ = E_0 \, i E_0 E_k = \] \[ = - E_0 i E_k E_0 = \] \[ = - \gamma_k \gamma_0 \] d.h. auch die \(\gamma_\mu\) -Matrizen (mit \(\mu = 0, 1, 2, 3\) erfüllen die Beziehung \[ \gamma_\mu \gamma_\nu + \gamma_\nu \gamma_\mu = 2 \, g_{\mu\nu} \] Explizit lauten diese Matrizen: \[ \gamma_0 = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \] \[ \gamma_k = \begin{pmatrix} 0 & \sigma_k \\ - \sigma_k & 0 \end{pmatrix} \] Das ist genau die Standard-Darstellung (Dirac-Darstellung) der sogenannten Dirac-Matrizen. Daneben gibt es natürlich die Matrixdarstellung, die wir oben hergeleitet haben, sowie beispielsweise die sogenannte Weyl-Darstellung. Die Weyl-Darstellung erhält man, wenn man die Standarddarstellung mit Hilfe der Matrix \[ U = \frac{1}{\sqrt{2}} \, \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \] über \[ \gamma'_\mu = U \gamma_\mu U \] umrechnet. Um mit üblichen Konventionen in konsistent zu sein, versehen wir die drei räumlichen \(\gamma_k\) -Matrizen zusätzlich noch mit einem Vorzeichen. Das Ergebnis für die Weyl-Darstellung lautet damit (den Strich lassen wir wieder weg – ab sofort schreiben wir \(\gamma_\mu\) für jede beliebige Darstellung der Clifford-Generatoren zur Minkowski-Raumzeit, also auch für die oben gebildeten quaternionischen \(E_\mu\)): \[ \gamma_0 = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \] \[ \gamma_k = \begin{pmatrix} 0 & \sigma_k \\ - \sigma_k & 0 \end{pmatrix} \] d.h. nur die \(\gamma_0\) -Matrix sieht anders aus. Man kann die Weyl-Darstellung noch etwas kompakter schreiben, indem wir wie gewohnt \[ \sigma_0 = 1 \] verwenden sowie \[ \tilde{\sigma}_0 := \sigma_0 = 1 \] \[ \tilde{\sigma}_k := - \sigma_k \] schreiben. Damit lautet die Weyl-Darstellung \[ \gamma_\mu = \begin{pmatrix} 0 & \sigma_\mu \\ \tilde{\sigma}_\mu & 0 \end{pmatrix} \] Mit Hilfe der Clifford-Algebra können wir nun zur Spin-Gruppe der Lorentzgruppe übergehen. Die entsprechende Gleichung \[ j(\boldsymbol{R} x) = R \, j(x) \, R^{-1} \] übersetzen wir dazu in die übliche Schreibweise, indem wir \( \Lambda \) statt \( \boldsymbol{R} \) und \(S\) statt \(R\) sowie \( \gamma(x) \) statt \( j(x) \) schreiben, d.h. \[ \gamma(x) = \gamma_\mu x^\mu \] Damit haben wir:
| \[ \gamma(\Lambda x) = S \, \gamma(x) \, S^{-1} \] |
Wir beschränken uns auf Lorentztransformationen, die sich stetig mit der \(1\) verbinden lassen. Für den Rotor \(S\) können wir dann (zumindest in der Nähe von \(1\)) schreiben: \[ S = e^{B/2} \] mit \[ B = \sum_{\mu \lt \nu} \, \alpha^{\mu\nu} \gamma_\mu \gamma_\nu \] Wieder wählen wir die reellen Parameter \(\alpha^{\mu\nu}\) antisymmetrisch in den Indices, so dass wir ggf. auch die Indices vertauschen können.
Anmerkung:
Man kann zeigen, dass man
bei der Lorentzgruppe jeden Rotor \(S\) entweder als
\( S = e^{B/2} \) oder als
\( S = - e^{B/2} \) schreiben kann.
Wir hatten das bereits am Schluss von Kapitel 4.10 erwähnt.
Hätte die Minkowski-Metrik zwei positive und zwei negative Einsen,
dann würde auch diese Aussage nicht mehr gelten.
Es gibt Elemente in der entsprechenden Spingruppe
\(Spin(2,2)\), die man nicht als \( \pm e^{B/2} \) schreiben kann.
Siehe dazu auch
Pertti Lounesto:
Counterexamples to theorems published and proved in recent literature on
Clifford algebras, spinors, spin groups and the exterior algebra.
Rechnen wir \( \gamma_\mu \gamma_\nu \) für \( \mu \lt \nu \) aus, wobei wir die obige Weyl-Darstellung verwenden, da diese sich hier als günstig erweist. \[ \gamma_\mu \gamma_\nu = \] \[ = \begin{pmatrix} 0 & \sigma_\mu \\ \tilde{\sigma}_\mu & 0 \end{pmatrix} \, \begin{pmatrix} 0 & \sigma_\nu \\ \tilde{\sigma}_\nu & 0 \end{pmatrix} = \] \[ = \begin{pmatrix} \sigma_\mu \tilde{\sigma}_\nu & 0 \\ 0 & \tilde{\sigma}_\mu \sigma_\nu \end{pmatrix} \] Das ist genau der Vorteil der Weyl-Darstellung hier: die Nicht-Diagonalblöcke sind Null. Rechnen wir weiter (mit \(i\) und \(k\) von 1 bis 3): \[ \gamma_0 \gamma_k = \] \[ = \begin{pmatrix} \sigma_0 \tilde{\sigma}_k & 0 \\ 0 & \tilde{\sigma}_0 \sigma_k \end{pmatrix} = \] \[ = \begin{pmatrix} - \sigma_k & 0 \\ 0 & \sigma_k \end{pmatrix} \] und \[ \gamma_i \gamma_k = \] \[ = \begin{pmatrix} \sigma_i \tilde{\sigma}_k & 0 \\ 0 & \tilde{\sigma}_i \sigma_k \end{pmatrix} = \] \[ = \begin{pmatrix} - \sigma_i \sigma_k & 0 \\ 0 & -\sigma_i \sigma_k \end{pmatrix} = \] \[ = \begin{pmatrix} - i \epsilon_{ikl} \sigma_l & 0 \\ 0 & - i \epsilon_{ikl} \sigma_l \end{pmatrix} \] Wenn wir \[ \alpha^{0 k} =: -\alpha^k \] schreiben sowie \[ \alpha^{12} =: w^3 \] (usw. zyklisch), dann ist \[ B = \sum_{\mu \lt \nu} \alpha^{\mu\nu} \gamma_\mu \gamma_\nu = \] \[ = \begin{pmatrix} \sigma(\boldsymbol{\alpha}) - i \sigma(\boldsymbol{w}) & 0 \\ 0 & -\sigma(\boldsymbol{\alpha}) - i \sigma(\boldsymbol{w}) \end{pmatrix} \] und somit \[ S = e^{B/2} = \] \[ = \begin{pmatrix} e^{\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} & 0 \\ 0 & e^{-\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} \end{pmatrix} \] Die beiden 2-mal-2-Blöcke in S kennen wir aus Kapitel 4.10. Kurze Wiederholung: \[ \quad \quad g = D^{\frac{1}{2}, 0}(g) = e^{ \frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} \] \[ (g^+)^{-1} = D^{0, \frac{1}{2}}(g) = e^{-\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} \] Die Matrix \(g\) ist also aus \(SL(2,\mathbb{C})\), und \(S\) hat in der Weyl-Darstellung die Form
| \[ S = \begin{pmatrix} g & 0 \\ 0 & (g^+)^{-1} \end{pmatrix} \] |
Setzen wir dies in die Gleichung \( \gamma(\Lambda x) = S \, \gamma(x) \, S^{-1} \) in der Weyl-Darstellung ein, so erhalten wir die beiden Gleichungen
| \[ g \, \sigma(x) \, g^+ = \sigma(\Lambda x) \] \[ (g^+ )^{-1} \, \tilde{\sigma}(x) \, g^{-1} = \tilde{\sigma}(\Lambda x) \] |
Die erste Gleichung ist genau der Zusammenhang zwischen der \(SL(2,\mathbb{C})\)-Matrix \(g\) aus der Überlagerungsgruppe (hier gleich Spingruppe) und der Lorentzmatrix \(\Lambda\), wobei wir uns aufgrund der Formel \( S = e^{B/2} \) auf Lorentzmatrizen beschränkt haben, die sich stetig mit der Eins verbinden lassen (also keine Raum- oder Zeit-Spiegelungen).
Die zweite Gleichung ist äquivalent zur ersten Gleichung. Kurzer Beweis: Aus \[ \sigma(x) \, \tilde{\sigma}(x) = x^2 \] mit \(x^2 = x^\mu x_\mu = (x^0)^2 - \boldsymbol{x}^2 \) folgt (einfach in der Mitte \(1 = g^+ \, (g^+ )^{-1}\) einfügen und Gleichung von links mit \(g\) und von rechts mit \(g^{-1}\) multiplizieren): \[ g \, \sigma(x) \, g^+ \, (g^+ )^{-1} \, \tilde{\sigma}(x) \, g^{-1} = x^2 \] Links können wir unsere erste Gleichung \( g \, \sigma(x) \, g^+ = \sigma(\Lambda x) \) verwenden und auf der rechten Seite ersetzen wir \( x^2 = (\Lambda x)^2 = \sigma(\Lambda x) \, \tilde{\sigma}(\Lambda x)\): \[ \sigma(\Lambda x) (g^+ )^{-1} \tilde{\sigma}(x) g^{-1} = \sigma(\Lambda x) \tilde{\sigma}(\Lambda x) \] Multiplikation von links mit \( \sigma(\Lambda x)^{-1} \) ergibt unsere zweite Gleichung \[ (g^+ )^{-1} \, \tilde{\sigma}(x) \, g^{-1} = \tilde{\sigma}(\Lambda x) \]
Da \(S\) gerade die beiden Fundamental-Darstellungen \[^ \quad \quad g = D^{\frac{1}{2}, 0}(g) \] \[ (g^+)^{-1} = D^{0, \frac{1}{2}}(g) \] in einzelnen Blöcken enthält, ist \(S\) aus der direkten Summe dieser beiden Fundamental-Darstellungen. Man schreibt auch, \(S\) ist aus \( (\frac{1}{2}, 0) + (0, \frac{1}{2}) \) und meint damit, dass \(S\) genau die obige Blockstruktur hat.
Natürlich gibt es hier noch sehr viel mehr zu untersuchen. Was geschieht beispielsweise, wenn wir Raumspiegelungen \( \Lambda x = (x^0, - \boldsymbol{x}) \) betrachten, die ja ebenfalls die Minkowski-Metrik invariant lassen? Man findet, dass dann beispielsweise die Matrix \( S = \gamma_0 \) eine mögliche Lösung der Gleichung \( \gamma(\Lambda x) = S \, \gamma(x) \, S^{-1} \) ist. Die obige Matrix \(S\) mit \(g\) und \((g^+ )^{-1}\) ist dagegen nur für Lorentztransformationen gültig, die sich stetig mit der \(1\) verbinden lassen.
Es ist uns damit gelungen, die Spingruppen für die Drehgruppe und die Lorentzgruppe (genauer deren Zusammenhangskomponente mit der Eins) zu ermitteln und die entsprechenden Gleichungen herzuleiten. Für die Drehgruppe ist die Spingruppe gleich \(SU(2)\), und für die Lorentzgruppe gleich \(SL(2,\mathbb{C})\) – das wussten wir bereits aus den früheren Kapiteln.
Die Clifford-Algebren ermöglichen es uns darüber hinaus, auch für allgemeinere orthogonale Gruppen die zugehörige Spingruppe zu ermitteln. Man verwendet dazu wie oben gesehen einfach die Formeln
| \[ E_\mu E_\nu + E_\nu E_\mu = 2 g_{\mu\nu} \] d.h. die \(E_\mu\) sind Generatoren der Clifford-Algebra, \[ X := j(x) := x^\mu E_\mu \] liefert die Einbettung des Vektorraums in die Clifford-Algebra, \[ g(\boldsymbol{R} x, \boldsymbol{R} x) = g(x,y) \] d.h. \(\boldsymbol{R}\) ist orthogonal im Vektorraum mit Metrik \(g\), \[ j(\boldsymbol{R} x) = R \, j(x) \, R^{-1} \] liefert den Zusammenhang zum Rotor \(R\) aus der Spingruppe \[ R = e^{B/2} \] ist der allgemeine Ansatz für den Rotor (zumindest nahe bei \(1\)) mit: \[ B = \sum_{\mu \lt \nu} \alpha^{\mu\nu} E_\mu E_\nu \] d.h. \(B\) ist ein Clifford-Bivektor. |
Wenn der Vektorraum \(V\), aus dem \(x\) stammt, eine höhere Dimension aufweist, so muss die Spingruppe keineswegs mit irgendeiner anderen Gruppe identisch sein. Es ist also ein Zufall, dass für den euklidischen dreidimensionalen Raum die Spingruppe gerade gleich \(SU(2)\) ist, oder dass sie für die Minkowski-Raumzeit gleich \(SL(2,\mathbb{C})\) ist.
Hier sind einige weitere solche Zufälle, die manchmal eine Rolle spielen können (siehe z.B. John Baez: Week 61 sowie Wikipedia: Spin group):
Für den vierdimensionalen euklidischen Raum mit der Drehgruppe SO(4) ist die Spingruppe gleich \(SU(2) \otimes SU(2)\) , d.h. man kann sie durch komplexe 4-mal-4-Matrizen der Form \[ \begin{pmatrix} u & 0 \\ 0 & u' \end{pmatrix} \] mit \(u\) und \(u'\) aus \(SU(2)\) darstellen. Das ist ganz ähnlich zur Gleichung \[ S = \begin{pmatrix} g & 0 \\ 0 & (g^+)^{-1} \end{pmatrix} \] \[ = = \begin{pmatrix} e^{\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} & 0 \\ 0 & e^{-\frac{1}{2} \sigma(\boldsymbol{\alpha}) - i \frac{1}{2} \sigma(\boldsymbol{w})} \end{pmatrix} \] für den Rotor zur Lorentzgruppe \(SO(1,3)\). Man muss in dieser Formel nur analytisch zu komplexen Parametern \(\boldsymbol{\alpha}\) und \(\boldsymbol{w}\) fortsetzen, so dass \[ \boldsymbol{\alpha} - i \boldsymbol{w} =: - i \boldsymbol{a} \] \[ - \boldsymbol{\alpha} - i \boldsymbol{w} =: - i \boldsymbol{a}' \] ist. Setzen wir dies in \(S\) ein, so ist \[ S = \begin{pmatrix} e^{- i \frac{1}{2} \sigma(\boldsymbol{a} )} & 0 \\ 0 & e^{- i \frac{1}{2} \sigma(\boldsymbol{a}')} \end{pmatrix} \] Auf der reellen Achse der Parameter \(\boldsymbol{a}\) und \(\boldsymbol{a}'\) ist diese Matrix gleich \[ \begin{pmatrix} u & 0 \\ 0 & u' \end{pmatrix} \] Allgemein hängen die Lorentzgrupppe \(SO(1,3)\) und die Gruppe \(SO(4)\) auf diese Weise über analytische Fortsetzung in den Parametern miteinander zusammen, wie man an den Exponentialdarstellungen der Gruppenelemente und der entsprechenden Clifford-Darstellung \( S = e^{B/2} \) der Spingruppe erkennen kann (wir überspringen das hier). Hinweise in diese Richtung haben wir bereits am Ende von Kapitel 4.10 gesehen, als wir die Lie-Algebra der Lorentzgruppe betrachtet haben.
Für den fünfdimensionalen euklidischen Raum mit der Drehgruppe \(SO(5)\) ist die Spingruppe gleich \(SP(2)\), die man auch als quaternionische unitäre Gruppe bezeichnet. Mehr dazu in Wikipedia: Symplectic group.
Für den sechsdimensionalen euklidischen Raum mit der Drehgruppe \(SO(6)\) ist die Spingruppe gleich \(SU(4)\) (die vierdimensionale speziell-unitären Matrizen).
Im sieben- und achtdimensionalen euklidischen Fall gibt es keine so klare Beziehung zwischen den Spingruppen und anderen Gruppen mehr, allerdings immer noch einige indirekte Zusammenhänge. Bei höheren Dimensionen ist auch das nicht mehr der Fall – die Spingruppen sind dann eigenständige neue Gruppen (siehe Wikipedia: Spin group).
Wir haben oben den Vektorraum \(V\) über die Abblidung \[ j(x) = X \] in die Clifford-Algebra eingebettet. Dabei wird die Clifford-Algebra dadurch festgelegt, dass wir die universelle Eigenschaft \[ E_\mu E_\nu + E_\nu E_\mu = 2 g_{\mu\nu} \] mit \(E_\mu = j(e_\mu) \) fordern, die man basisfrei auch als \[ X Y + Y X = 2 \, g(x,y) \] schreiben kann.
Im Grunde erzeugt man dadurch ausgehend von dem Vektorraum \(V\) eine passende Clifford-Algebra. Es wäre daher naheliegend, direkt den Vektorraum \(V\) zu verwenden und ihn einfach zu der entsprechenden Clifford-Algebra zu erweitern, anstatt ihn in die Clifford-Algebra einzubetten. Die Abbildung \(j\) entfällt damit und wir müssen nur eine passende Multiplikation zwischen den Vektoren einführen, die der Clifford-Multiplikation entspricht. Statt \( X Y \)schreiben wir dann direkt \( x y \).
Man könnte auch sagen: Man spart sich in den Formeln den Schritt von \(x\) nach \(X\) und die begriffliche Unterscheidung zwischen dem Vektor \(x\) und dem zugehörigen Clifford-Algebra-Element \(X\). Entsprechend stellt man sich auch meist keine Matrizen mehr für \(x\) oder \(y\) vor, auch wenn man das Ganze natürlich jederzeit in eine Matrixdarstellung übersetzen kann.
Analog zu oben könnte man die Clifford-Multiplikation über die Forderung \[ x y + y x = 2 \, g(x,y) \] und die üblichen Regeln für Multiplikation (analog zu Matrizen, also ohne Kommutativgesetz) festlegen.
Meist geht man aber etwas anders vor, da man oft die sogenannte Graßmann-Algebra (man nennt sie auch äußere Algebra) bereits definiert hat (siehe beispielsweise Kapitel 6.1). Das äußere Produkt (auch Graßmann- oder Dach-Produkt genannt) \(x \wedge y \) zweier Vektoren ist dabei im Wesentlichen durch seine Antisymmetrie gekennzeichnet: \[ x \wedge y = - y \wedge x \] (\( \wedge \) ist hier keine Lorentz-Matrix, sondern das antisymmetrische Produkt-Symbol). Die universelle Eigenschaft der Clifford-Algebra betrifft dagegen den symmetrisierten Teil des Clifford-Produktes. Es liegt daher nahe, das Clifford-Produkt in seinen symmetrischen und seinen antisymmetrischen Teil aufzuteilen, für den symmetrischen Teil dann die universelle Eigenschaft zu verwenden und den antisymmetrischen Teil mit dem äußeren Produkt zu identifizieren: \[ x y = \] \[ = \frac{1}{2} \, (x y + y x) + \] \[ \; + \frac{1}{2} \, (x y - y x) = \] \[ = g(x,y) + x \wedge y \] mit \[ x \wedge y := \frac{1}{2} \, (x y - y x) \] wenn man das Clifford-Produkt \( x y \) als gegeben ansieht und daraus das äußere Produkt definiert. Sieht man umgekehrt das äußere Produkt (und natürlich die Metrik) als gegeben an, dann kann man das Clifford-Produkt zweier Vektoren \(x\) und \(y\) entsprechend über
| \[ x y := g(x,y) + x \wedge y \] |
definieren. Die symmetrische Metrik \(g(x,y)\) wird in diesem Zusammenhang auch als inneres Produkt bezeichnet, passend zum antisymmetrischen äußeren Produkt \( x \wedge y \).
Graßmann selbst bezeichnete seinerzeit das Clifford-Produkt als zentrales Produkt. Heute wird es oft als geometrisches Produkt bezeichnet – daher der Begriff Geometrische Algebra. Man sollte sich aber nicht verwirren lassen: Geometrische Algebra ist Clifford-Algebra und geometrisches Produkt ist Clifford-Produkt.
Die Generatoren der Algebra sind nun einfach die Basisvektoren \(e_\mu\) des Vektorraums. Das Clifford-Produkt ungleicher Basisvektoren ist identisch mit dem äußeren Produkt dieser Vektoren. Daher können wir beispielsweise statt dem früheren \( E_1 E_2 \) hier \( e_1 \wedge e_2 \) schreiben.
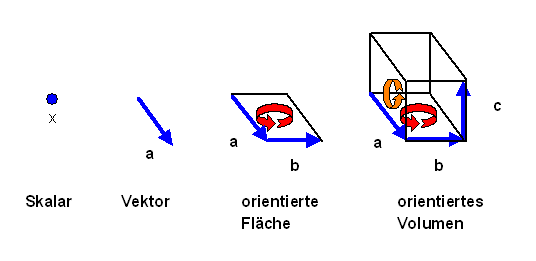
Die Basis der Clifford-Algebra ( = Geometrischen Algebra) zum dreidimensionalen Raum \(\mathbb{R}^3\) wäre dann gegeben durch \[ 1 \] \[ e_1 , \, e_2 , \, e_3 \] \[ e_1 \wedge e_2 , \, e_2 \wedge e_3 , \, e_3 \wedge e_1 \] \[ e_1 \wedge e_2 \wedge e_3 \] wobei die \(e_i\) eine Orthonormalbasis im Vektorraum bilden sollen.
Linearkombinationen der Basisvektoren der ersten Zeile nennt man Skalare, die der zweiten Zeile nennt man Vektoren, die der dritten Zeile nennt man Bi-Vektoren, und die der vierten Zeile nennt man Tri-Vektoren.
Skalare und Vektoren kennen wir bereits vom Vektorraum her. Bi-Vektoren sind uns bereits bei der Darstellung der Rotoren \( S = e^{B/2} \) begegnet: \(B\) war ein Bi-Vektor. Bleibt die Frage: kann man analog zu den Vektoren auch die Bi- und Tri-Vektoren im dreidimensionalen euklidischen Raum geometrisch interpretieren?
Schauen wir uns dazu das äußere Produkt zweier Vektoren an: \[ a \wedge b = \] \[ = (a^1 e_1 + a^2 e_2 + a^3 e_3) \wedge \] \[ \wedge \; (b^1 e_1 + b^2 e_2 + b^3 e_3) = \] \[ = (a^1 b^2 - a^2 b1) \, e_1 \wedge e_2 + \] \[ + \; (a^2 b^3 - a^3 b^2) \, e_2 \wedge e_3 + \] \[ + (a^3 b^1 - a^1 b^3) \, e_3 \wedge e_1 \] Aus der dreidimensionalen Vektorrechnung kennen wir das: Wenn wir \( e_1 \wedge e_2 \) durch \( e_3 \) ersetzen würden (usw. zyklisch), dann würde aus \( a \wedge b \) das Kreuzprodukt \( a \times b \) entstehen. Das wäre ein Vektor, dessen Länge gleich der von \(a\) und \(b\) aufgespannten Parallelogrammfläche ist, und dessen Richtung senkrecht zu \(a\) und \(b\) nach der rechte-Hand-Regel gegeben ist.
Nun kann man die Ersetzung von \( e_1 \wedge e_2 \) durch \(e_3\) (usw. zyklisch) durch Clifford-Multiplikation mit dem Pseudoskalar \[ - V := - e_1 \wedge e_2 \wedge e_3 \] erreichen (\(V\) ist hier also nicht der Vektorraum; oft schreibt man auch \(i\) statt \(V\)). So ist beispielsweise \[ (e_1 \wedge e_2 \wedge e_3) (e_1 \wedge e_2) = \] \[ = e_1 e_2 e_3 e_1 e_2 = \] \[ = e_2 e_3 e_1 e_1 e_2 = \] \[ = e_2 e_3 e_2 = \] \[ = - e_2 e_2 e_3 = \] \[ = - e_3 \] Insgesamt ist \[ - V \, (a \wedge b) = (a \times b) \] In diesem Sinn repräsentiert \( (a \wedge b) \) Fläche und Orientierung des Parallelogramms. Man sagt auch, die Bivektoren entsprechen in diesem Sinn den axialen Vektoren, wobei es aber auch Bivektoren gibt, die sich nicht als \( (a \wedge b) \) schreiben lassen. Die Multiplikation mit \( - V \) weist übrigens deutliche Ähnlichkeit mit dem Hodge-Sternoperator auf (siehe Kapitel 5.1.12).
Wir wollen hier nicht weiter ins Detail gehen.
Es zeigt sich, dass Clifford-Algebren bzw. die Geometrische Algebra einen Rahmen bilden,
in dem sich große Teile der Mathematik formulieren lassen, insbesondere die Wirkung von
Symmetriegruppen. Mehr dazu siehe im Internet in
Wikipedia: Geometric algebra,
oder in
Chris J.L. Doran: Geometric Algebra and its Application to Mathematical Physics sowie in
Douglas Lundholm: Geometric Algebra and its Applications to Physics.
So – das wäre geschafft. Im Grunde war das Thema gar nicht so kompliziert, wie ich zunächst gedacht hatte. Bei der Betrachtung der Dirac-Gleichung wird uns dieser Einblick in die Clifford-Algebren noch gute Dienste leisten. Doch zunächst wollen wir uns im nächsten Kapitel einer einfacheren Gleichung zuwenden: der Klein-Gordon-Gleichung.
© Jörg Resag, www.joerg-resag.de
last modified on 21 August 2023